【冀教版】2017年春九下数学:32.1《投影》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:32.1《投影》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 13:31:07 | ||
图片预览





文档简介
课件12张PPT。九年级数学·下 新课标[冀教]第三十二章 投影与视图32.1 投 影学 习 新 知北京故宫中的日晷闻名世界,是我国光辉灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影子的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.认识概念【思考1】
1.灯泡的光线与探照灯的光线有什么区别?
2.蜡烛的光线、太阳光线分别与哪种光线相同?
3.你能举出生活中的一些实例吗?(灯泡的光线可以看做是从一点射出的,探照灯的光线可以看做是平行的)(蜡烛的光线与灯泡的光线相同,太阳光线与探照灯的光线相同)物体在光线的照射下,会在某个平面(墙面、地面等所在的平面)上留下它的影子,这种现象就是投影.光线是投影线,这个平面是投影面.蜡烛和灯泡的光线可以看做是从一点射出的.像这样,由一点射出的光线照射在物体上所形成的投影,叫做中心投影.太阳光线和探照灯的光线可以看做是平行的.像这样,由平行光线照射在物体上所形成的投影,叫做平行投影.【思考2】
观察平行投影和中心投影,它们有什么相同点与不同点?平行投影与中心投影的区别与联系平行的
投射线从一点出发
的投射线全等放大(位
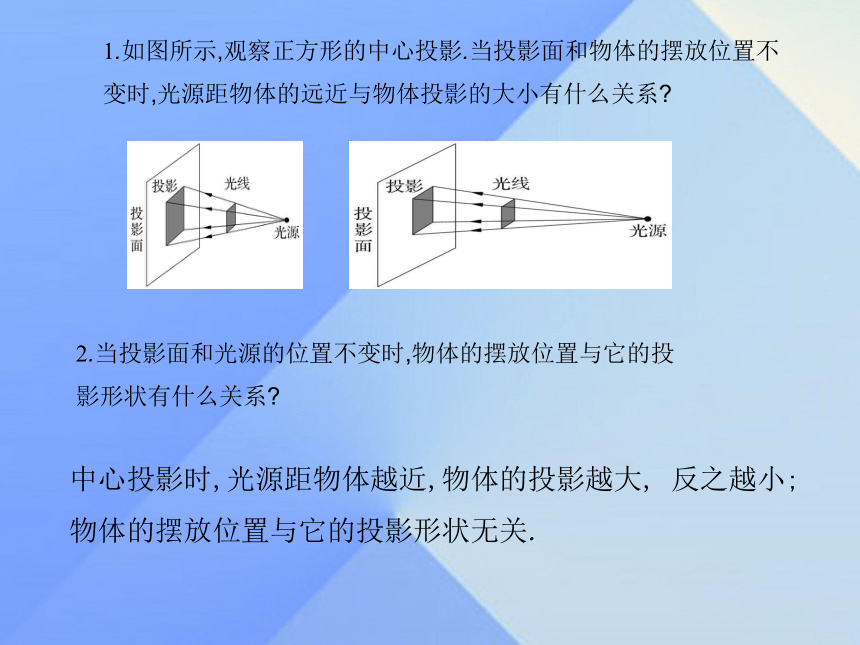
似变换)都是物体在光线的照射下,在某个平面内形成的影子(都是投影)1.如图所示,观察正方形的中心投影.当投影面和物体的摆放位置不变时,光源距物体的远近与物体投影的大小有什么关系?2.当投影面和光源的位置不变时,物体的摆放位置与它的投影形状有什么关系?中心投影时,光源距物体越近,物体的投影越大, 反之越小;物体的摆放位置与它的投影形状无关.一起探究1.同一时刻,同一物体的平行投影大小相同;同一时刻,不同物体的平行投影的长与物体的高的比相等.3.正投影:我们把投影线垂直照射在投影面上的物体的投影叫做正投影.2.平行投影时,物体的摆放位置离地面的远近与它的投影的形状没有关系;物体摆放的位置不同,则它的投影的形状不同,如正方形的平行投影可能是正方形、长方形或一条线段.追加思考:
1.三角形在平行投影下的形状是什么?圆呢?
2.三角形的正投影是什么图形?观察与思考如图所示,已知正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.(1)四边形A'B'C'D'是什么四边形?正方体R面对面的正投影是什么图形?
(2)正方体Q面和P面的正投影分别是什么图形?
(3)正方体棱AB和棱AE的正投影分别是什么图形?正方体顶点A和顶点E的正投影分别是什么图形?(1)四边形A'B'C'D'是正方形.R面的对面的正投影是正方形.
(2)Q面与P面的正投影均为线段.
(3)棱AB的正投影是线段且与AB等长,棱AE的正投影是一个点;顶点A和顶点E的正投影仍是一个点.结论:
点的正投影是点;线的正投影是线或点;面的正投影是面或线.6.只有在平行投影中,才会出现正投影.正投影是光线与投影面的关系,与物体的摆放位置无关.
人们在实际作图中,经常采用正投影.[知识拓展]1.光线移动时,物体影子的大小、方向也随着变化,物体的形状与影子的形状有密切的联系.2.光是沿直线传播的,因此我们可以由投影与物体确定光线方向.3.平行投影的应用:(1)根据阳光下影子的大小、位置的变化判断时刻的不同;(2)已知一个物体及其在阳光下的影子,可作出同一时刻另一个物体在阳光下的影子;(3)根据物高和影长的关系可以求物高或影长.4.中心投影的应用:(1)根据点光源下两种或两种以上物体及影子的情况判断点光源的位置;(2)已知点光源的位置,可以画物体在点光源下的影子.5.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.检测反馈1.平行投影中的光线是 ( )
A.平行的 B.聚成一点的
C.不平行的 D.向四面八方发散的解析:平行投影中的光线是平行的.故选A.A解析:中心投影的光源为灯光,平行投影的光源为阳光与月光,在各选项中只有D选项得到的投影为中心投影.故选D.2.下列投影中属于中心投影的是 ( )
A.阳光下跑动的运动员的影子
B.阳光下木杆的影子
C.阳光下汽车的影子
D.路灯下行人的影子D3.如图所示,箭头表示投影的方向,则图中圆柱体的正投影是 ( )
A.圆 B.矩形
C.梯形 D.圆柱解析:圆柱的正投影是矩形.故选B.B 4.小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图所示,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2 m,又测得CE=0.8 m,CA=30 m(点A,E,C在同一直线上).
已知小明的身高EF是1.7 m,请你帮小明求出楼高AB(结果精确到0.1 m).解:如图所示,过点D作DG⊥AB,分别交AB,EF于点G,H,则EH=AG=CD=1.2,
DH=CE=0.8,DG=CA=30.∵EF∥AB,∴
由题意得FH=EF-EH=1.7-1.2=0.5.
∴ 解得BG=18.75.
∴AB=BG+AG=18.75+1.2=19.95≈20.0.
∴楼高AB约为20.0 m.
1.灯泡的光线与探照灯的光线有什么区别?
2.蜡烛的光线、太阳光线分别与哪种光线相同?
3.你能举出生活中的一些实例吗?(灯泡的光线可以看做是从一点射出的,探照灯的光线可以看做是平行的)(蜡烛的光线与灯泡的光线相同,太阳光线与探照灯的光线相同)物体在光线的照射下,会在某个平面(墙面、地面等所在的平面)上留下它的影子,这种现象就是投影.光线是投影线,这个平面是投影面.蜡烛和灯泡的光线可以看做是从一点射出的.像这样,由一点射出的光线照射在物体上所形成的投影,叫做中心投影.太阳光线和探照灯的光线可以看做是平行的.像这样,由平行光线照射在物体上所形成的投影,叫做平行投影.【思考2】
观察平行投影和中心投影,它们有什么相同点与不同点?平行投影与中心投影的区别与联系平行的
投射线从一点出发
的投射线全等放大(位
似变换)都是物体在光线的照射下,在某个平面内形成的影子(都是投影)1.如图所示,观察正方形的中心投影.当投影面和物体的摆放位置不变时,光源距物体的远近与物体投影的大小有什么关系?2.当投影面和光源的位置不变时,物体的摆放位置与它的投影形状有什么关系?中心投影时,光源距物体越近,物体的投影越大, 反之越小;物体的摆放位置与它的投影形状无关.一起探究1.同一时刻,同一物体的平行投影大小相同;同一时刻,不同物体的平行投影的长与物体的高的比相等.3.正投影:我们把投影线垂直照射在投影面上的物体的投影叫做正投影.2.平行投影时,物体的摆放位置离地面的远近与它的投影的形状没有关系;物体摆放的位置不同,则它的投影的形状不同,如正方形的平行投影可能是正方形、长方形或一条线段.追加思考:
1.三角形在平行投影下的形状是什么?圆呢?
2.三角形的正投影是什么图形?观察与思考如图所示,已知正方体的R面与投影面是平行的,它在投影面上的正投影是四边形A'B'C'D'.(1)四边形A'B'C'D'是什么四边形?正方体R面对面的正投影是什么图形?
(2)正方体Q面和P面的正投影分别是什么图形?
(3)正方体棱AB和棱AE的正投影分别是什么图形?正方体顶点A和顶点E的正投影分别是什么图形?(1)四边形A'B'C'D'是正方形.R面的对面的正投影是正方形.
(2)Q面与P面的正投影均为线段.
(3)棱AB的正投影是线段且与AB等长,棱AE的正投影是一个点;顶点A和顶点E的正投影仍是一个点.结论:
点的正投影是点;线的正投影是线或点;面的正投影是面或线.6.只有在平行投影中,才会出现正投影.正投影是光线与投影面的关系,与物体的摆放位置无关.
人们在实际作图中,经常采用正投影.[知识拓展]1.光线移动时,物体影子的大小、方向也随着变化,物体的形状与影子的形状有密切的联系.2.光是沿直线传播的,因此我们可以由投影与物体确定光线方向.3.平行投影的应用:(1)根据阳光下影子的大小、位置的变化判断时刻的不同;(2)已知一个物体及其在阳光下的影子,可作出同一时刻另一个物体在阳光下的影子;(3)根据物高和影长的关系可以求物高或影长.4.中心投影的应用:(1)根据点光源下两种或两种以上物体及影子的情况判断点光源的位置;(2)已知点光源的位置,可以画物体在点光源下的影子.5.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.检测反馈1.平行投影中的光线是 ( )
A.平行的 B.聚成一点的
C.不平行的 D.向四面八方发散的解析:平行投影中的光线是平行的.故选A.A解析:中心投影的光源为灯光,平行投影的光源为阳光与月光,在各选项中只有D选项得到的投影为中心投影.故选D.2.下列投影中属于中心投影的是 ( )
A.阳光下跑动的运动员的影子
B.阳光下木杆的影子
C.阳光下汽车的影子
D.路灯下行人的影子D3.如图所示,箭头表示投影的方向,则图中圆柱体的正投影是 ( )
A.圆 B.矩形
C.梯形 D.圆柱解析:圆柱的正投影是矩形.故选B.B 4.小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图所示,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2 m,又测得CE=0.8 m,CA=30 m(点A,E,C在同一直线上).
已知小明的身高EF是1.7 m,请你帮小明求出楼高AB(结果精确到0.1 m).解:如图所示,过点D作DG⊥AB,分别交AB,EF于点G,H,则EH=AG=CD=1.2,
DH=CE=0.8,DG=CA=30.∵EF∥AB,∴
由题意得FH=EF-EH=1.7-1.2=0.5.
∴ 解得BG=18.75.
∴AB=BG+AG=18.75+1.2=19.95≈20.0.
∴楼高AB约为20.0 m.
