【冀教版】2017年春九下数学32.3《直棱柱和圆锥的侧面展开图》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学32.3《直棱柱和圆锥的侧面展开图》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 12:01:24 | ||
图片预览



文档简介
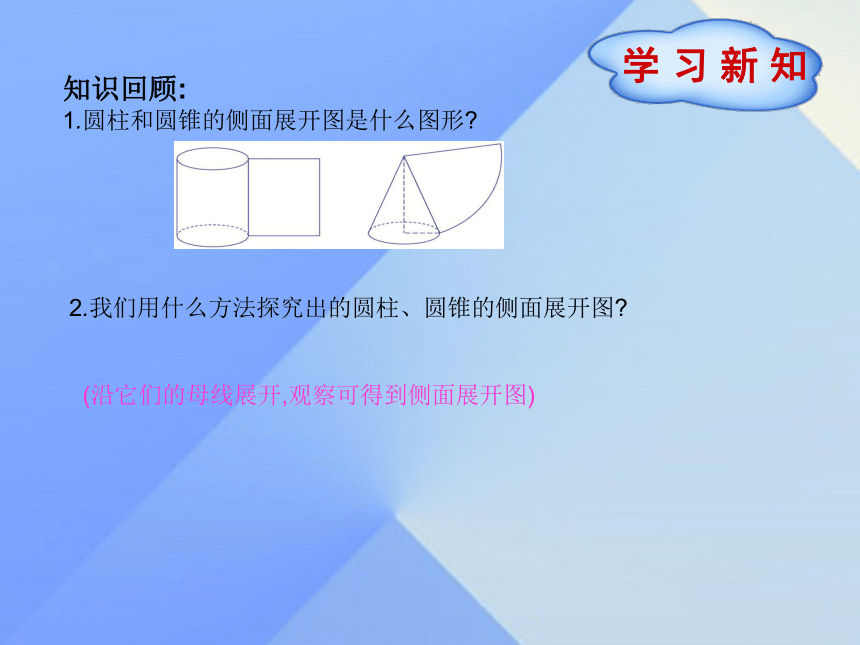
课件13张PPT。九年级数学·下 新课标[冀教]第三十二章 投影与视图32.3 直棱柱和圆锥的侧面展开图学 习 新 知知识回顾:
1.圆柱和圆锥的侧面展开图是什么图形?2.我们用什么方法探究出的圆柱、圆锥的侧面展开图?(沿它们的母线展开,观察可得到侧面展开图)观察与思考如图所示,底面为正六边形的六棱柱,沿它的一条侧棱展开,就得到了这个六棱柱的侧面展开图.思考:
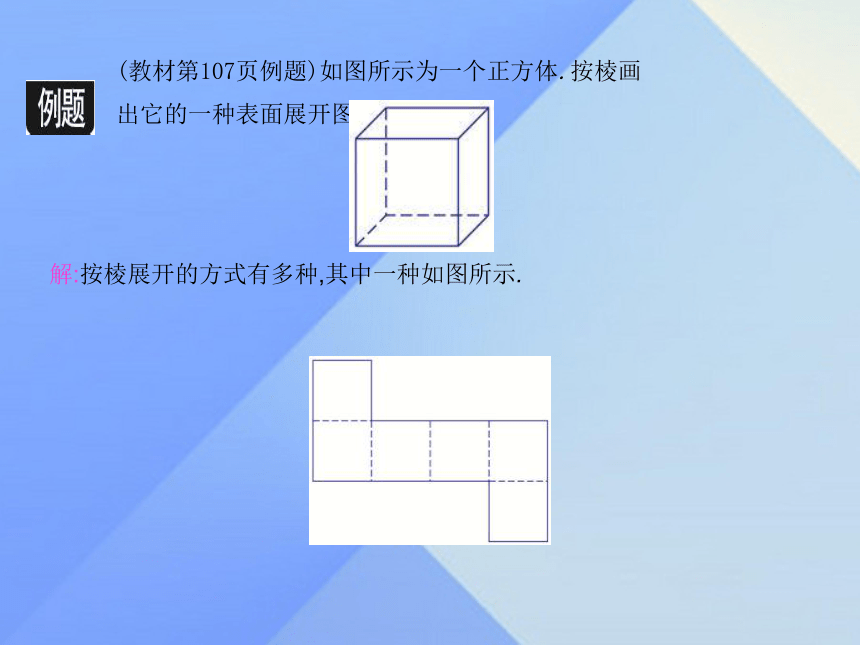
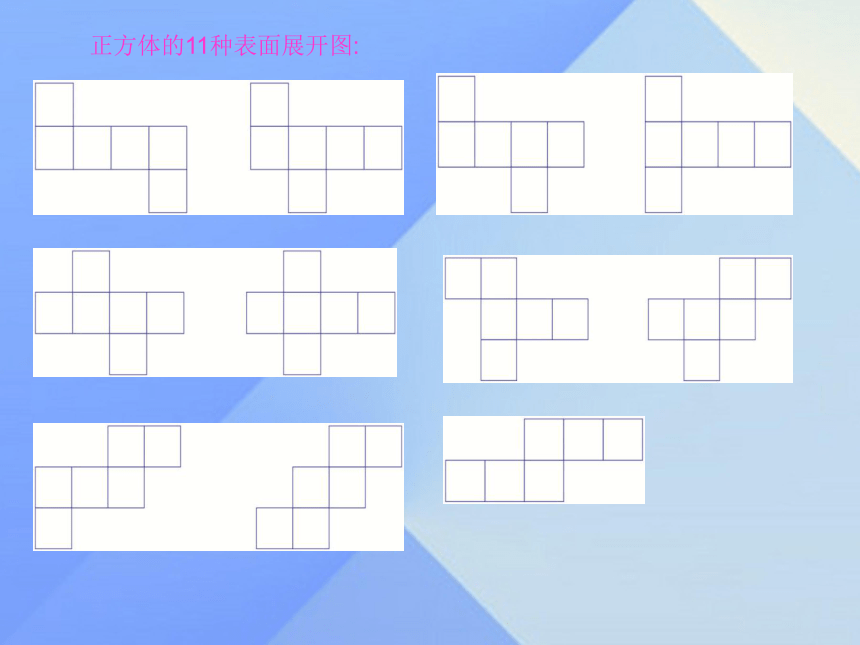
1.在上图中,六棱柱的侧面展开图为长方形.这个长方形的长和宽分别与棱柱底面的周长和侧棱长有什么关系?2.如图所示,底面为多边形的棱柱侧面展开图是长方形吗?如果是长方形,那么它的长和宽分别与棱柱底面的周长和侧棱长有什么关系?结论:直棱柱的侧面展开图是长方形,长方形的长是直棱柱的底面周长,长方形的宽是直棱柱的侧棱长.大家谈谈如图所示,已知三个棱柱的侧面展开图,请说说它们分别是什么样的棱柱.(1)在硬纸片上画一个半径为6 cm,圆心角为216°的扇形.将这个扇形剪下来,按如图所示的方式围成一个圆锥的侧面.指出这个圆锥的母线长.做一做(2)用一块硬纸片剪出这个圆锥的底面,和(1)中圆锥的侧面一起做成一个圆锥.(黏合部分忽略不计)结论:扇形的半径为围成的圆锥的母线长,扇形的弧长为围成的圆锥的底面周长.(教材第107页例题)如图所示为一个正方体.按棱画出它的一种表面展开图.解:按棱展开的方式有多种,其中一种如图所示.正方体的11种表面展开图:如图所示,已知一个长方体纸箱的长、宽和高分别为30 cm,20 cm,10 cm.一只昆虫从纸箱的顶点A处沿纸箱表面ACDE和表面GEDB爬到另一个顶点B处.它沿哪条路线爬行的距离最短?请说明理由,并求出这个最短距离.(结果保留两位小数)共同探究思考:
1.长方体有几种展开方式,使得点A与点B在同一个平面上?
2.在同一平面上如何求两点之间的最短距离?
3.长方体的展开图中,哪个展开图中A,B两点之间的距离最短?解:如图所示,将这个长方体纸箱的表面展开,连接AB.根据“两点之间线段最短”,可知线段AB就是昆虫爬行距离最短的路线.在Rt△ABC中,AC=30 cm,BC=BD+CD=20+10=30(cm).
根据勾股定理,得:≈42.43(cm),
即昆虫最短爬行路线的距离约为42.43 cm.2.常见图形的侧面展开图:圆锥的侧面展开图是一个扇形,其中扇形的半径是圆锥的母线长,扇形的弧长是底面圆的周长;圆柱的侧面展开图是矩形,矩形的一边长是圆柱的底面周长,另一边长是圆柱的高;正方体的表面展开图有11种情况;棱柱的侧面展开图是矩形,矩形的一边长是棱柱的底面周长,另一边长是棱柱的侧棱长.[知识拓展] 1.立体图形是由面围成的,同一个立体图形,沿不同方式展开,得到的平面图形是不同的.检测反馈1.下面的图形中,是三棱柱的侧面展开图的是 ( )解析:棱柱的侧面展开图是矩形,三棱柱的侧面展开图是3个矩形.故选A.A2.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图所示),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是 ( )解析:A中展开图“预”的对面是“考”,不符合要求,故A错误;B中“预”的对面是“功”,不符合要求,故B错误;C中“预”的对面是“中”,“成”的对面是“功”,符合题意,故C正确;D中“预”的对面是“中”,“成”的对面是“祝”,不符合题意,故D错误.故选C.C3.如果圆锥的母线长为5 cm,底面半径为3 cm,那么圆锥的全面积为 .?解析:圆锥的侧面积为 ×5×(3×2×π)=15π(cm2),底面积为π×32=9π(cm2),所以圆锥的全面积为15π+9π=24π(cm2).故填24π cm2.24π cm24.如图所示的是一个食品包装盒的平面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面积之和).解:(1)这个多面体是正六棱柱.
(2)S侧=6ab ,S底= 6× b2= b2,
所以S全面积=S侧+2S底=6ab+3 b2.
1.圆柱和圆锥的侧面展开图是什么图形?2.我们用什么方法探究出的圆柱、圆锥的侧面展开图?(沿它们的母线展开,观察可得到侧面展开图)观察与思考如图所示,底面为正六边形的六棱柱,沿它的一条侧棱展开,就得到了这个六棱柱的侧面展开图.思考:
1.在上图中,六棱柱的侧面展开图为长方形.这个长方形的长和宽分别与棱柱底面的周长和侧棱长有什么关系?2.如图所示,底面为多边形的棱柱侧面展开图是长方形吗?如果是长方形,那么它的长和宽分别与棱柱底面的周长和侧棱长有什么关系?结论:直棱柱的侧面展开图是长方形,长方形的长是直棱柱的底面周长,长方形的宽是直棱柱的侧棱长.大家谈谈如图所示,已知三个棱柱的侧面展开图,请说说它们分别是什么样的棱柱.(1)在硬纸片上画一个半径为6 cm,圆心角为216°的扇形.将这个扇形剪下来,按如图所示的方式围成一个圆锥的侧面.指出这个圆锥的母线长.做一做(2)用一块硬纸片剪出这个圆锥的底面,和(1)中圆锥的侧面一起做成一个圆锥.(黏合部分忽略不计)结论:扇形的半径为围成的圆锥的母线长,扇形的弧长为围成的圆锥的底面周长.(教材第107页例题)如图所示为一个正方体.按棱画出它的一种表面展开图.解:按棱展开的方式有多种,其中一种如图所示.正方体的11种表面展开图:如图所示,已知一个长方体纸箱的长、宽和高分别为30 cm,20 cm,10 cm.一只昆虫从纸箱的顶点A处沿纸箱表面ACDE和表面GEDB爬到另一个顶点B处.它沿哪条路线爬行的距离最短?请说明理由,并求出这个最短距离.(结果保留两位小数)共同探究思考:
1.长方体有几种展开方式,使得点A与点B在同一个平面上?
2.在同一平面上如何求两点之间的最短距离?
3.长方体的展开图中,哪个展开图中A,B两点之间的距离最短?解:如图所示,将这个长方体纸箱的表面展开,连接AB.根据“两点之间线段最短”,可知线段AB就是昆虫爬行距离最短的路线.在Rt△ABC中,AC=30 cm,BC=BD+CD=20+10=30(cm).
根据勾股定理,得:≈42.43(cm),
即昆虫最短爬行路线的距离约为42.43 cm.2.常见图形的侧面展开图:圆锥的侧面展开图是一个扇形,其中扇形的半径是圆锥的母线长,扇形的弧长是底面圆的周长;圆柱的侧面展开图是矩形,矩形的一边长是圆柱的底面周长,另一边长是圆柱的高;正方体的表面展开图有11种情况;棱柱的侧面展开图是矩形,矩形的一边长是棱柱的底面周长,另一边长是棱柱的侧棱长.[知识拓展] 1.立体图形是由面围成的,同一个立体图形,沿不同方式展开,得到的平面图形是不同的.检测反馈1.下面的图形中,是三棱柱的侧面展开图的是 ( )解析:棱柱的侧面展开图是矩形,三棱柱的侧面展开图是3个矩形.故选A.A2.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图所示),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是 ( )解析:A中展开图“预”的对面是“考”,不符合要求,故A错误;B中“预”的对面是“功”,不符合要求,故B错误;C中“预”的对面是“中”,“成”的对面是“功”,符合题意,故C正确;D中“预”的对面是“中”,“成”的对面是“祝”,不符合题意,故D错误.故选C.C3.如果圆锥的母线长为5 cm,底面半径为3 cm,那么圆锥的全面积为 .?解析:圆锥的侧面积为 ×5×(3×2×π)=15π(cm2),底面积为π×32=9π(cm2),所以圆锥的全面积为15π+9π=24π(cm2).故填24π cm2.24π cm24.如图所示的是一个食品包装盒的平面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面积之和).解:(1)这个多面体是正六棱柱.
(2)S侧=6ab ,S底= 6× b2= b2,
所以S全面积=S侧+2S底=6ab+3 b2.
