第三节 线段的垂直平分线 课时2同步练习
文档属性
| 名称 | 第三节 线段的垂直平分线 课时2同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 485.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-06 00:00:00 | ||
图片预览


文档简介
第三节线段的垂直平分线
第2课时 线段垂直平分线的应用
基础检测
知识点1三角形三边的垂直平分线
1.到三角形三个顶点距离相等的点,是三角形三条边的 的交点,即三角形三条边的垂直平分线交于 .?21世纪教育网版权所有
2.平面内到不在同一条直线上的三个点A,B,C的距离相等的点有( )
A.0个 B.1个 C.2个 D.3个
3.如图,地面上有三个洞口A,B,C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及三个洞口(到A,B,C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )21cnjy.com
A.△ABC三边垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
4.已知△ABC三边的垂直平分线的交点在△ABC的边上,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
5.(2015·泰州)如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
知识点2线段垂直平分线的作图及应用
6.(2015·北京)阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线
已知:线段AB
小芸的作法如下:
如图,(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C,D两点;
(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是?
.?
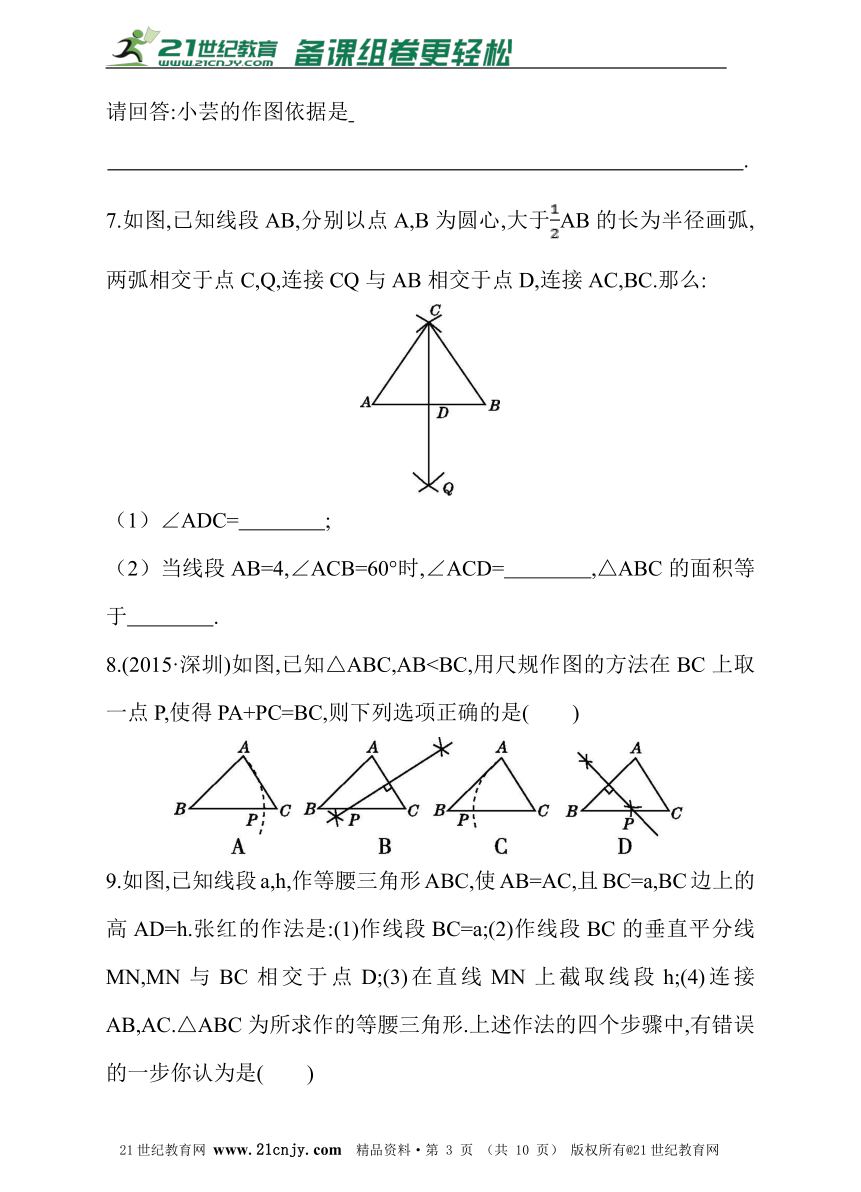
7.如图,已知线段AB,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点C,Q,连接CQ与AB相交于点D,连接AC,BC.那么:
(1)∠ADC= ;?
(2)当线段AB=4,∠ACB=60°时,∠ACD= ,△ABC的面积等于 .?
8.(2015·深圳)如图,已知△ABC,AB9.如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC.△ABC为所求作的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是( )www.21-cn-jy.com
A.(1) B.(2) C.(3) D.(4)
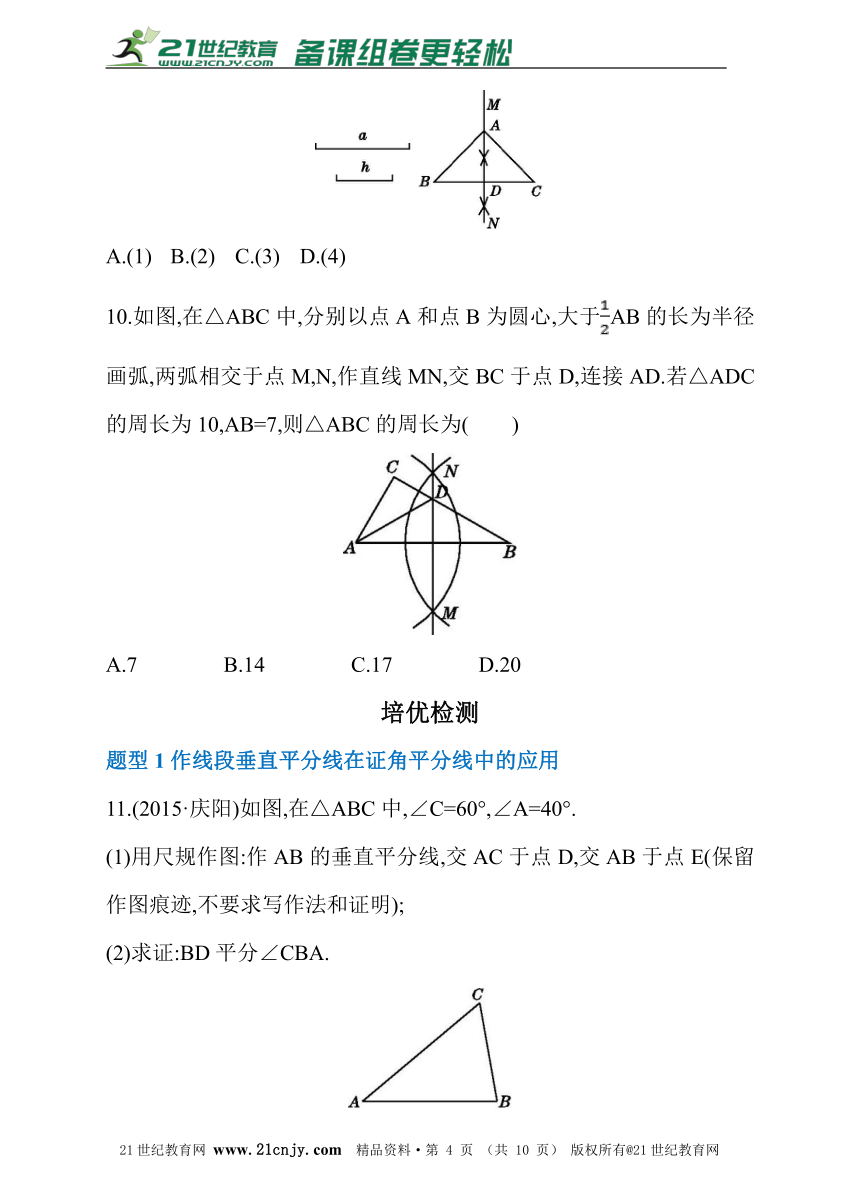
10.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )2·1·c·n·j·y
A.7 B.14 C.17 D.20
培优检测
题型1作线段垂直平分线在证角平分线中的应用
11.(2015·庆阳)如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图:作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);【来源:21·世纪·教育·网】
(2)求证:BD平分∠CBA.
题型2作线段垂直平分线在求边、角中的应用
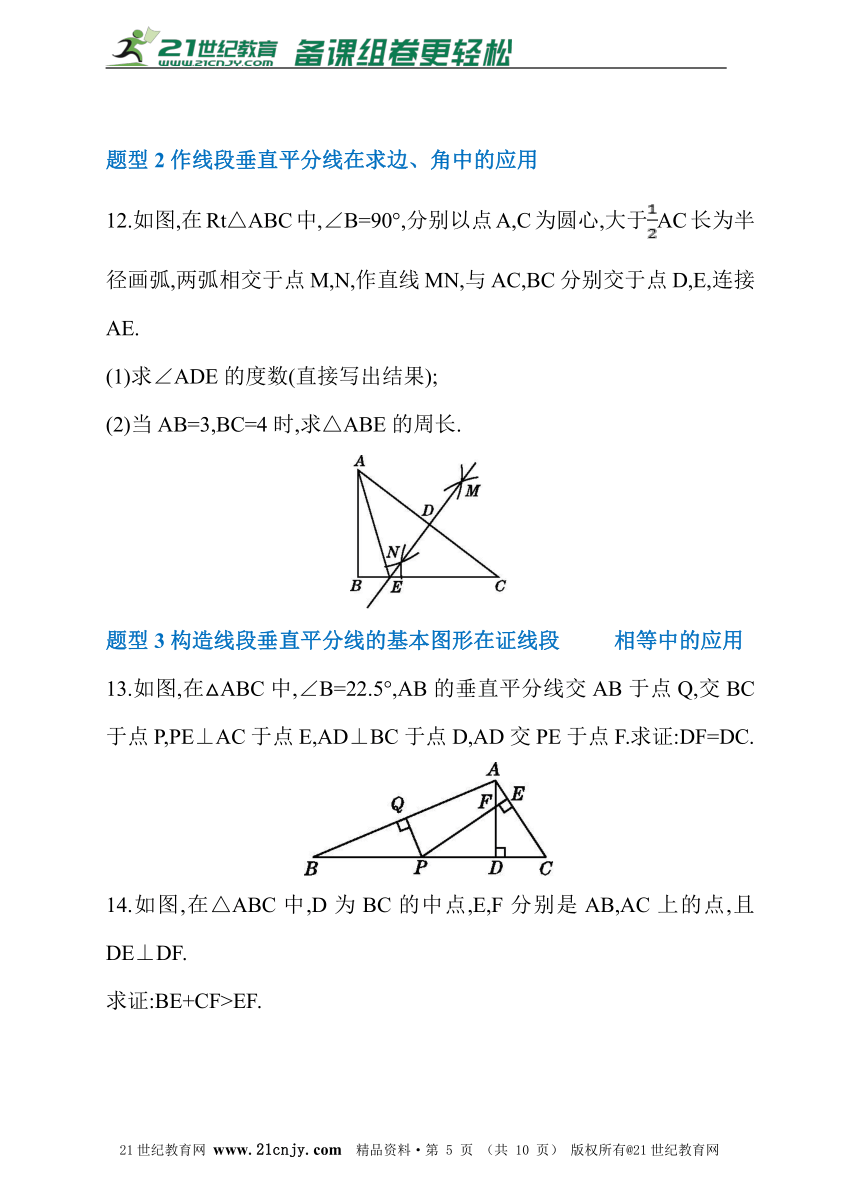
12.如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,E,连接AE.21·世纪*教育网
(1)求∠ADE的度数(直接写出结果);
(2)当AB=3,BC=4时,求△ABE的周长.
题型3构造线段垂直平分线的基本图形在证线段 相等中的应用
13.如图,在△ABC中,∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.
14.如图,在△ABC中,D为BC的中点,E,F分别是AB,AC上的点,且DE⊥DF.
求证:BE+CF>EF.
参考答案
1.【答案】垂直平分线;一点
2.【答案】B
解:首先到AB两点距离相等的点,这些点的集合是AB的中垂线
同样,到BC两点距离相等的点的集合是BC的中垂线
那么要ABC都距离相等,就是AB的中垂线与BC中垂线的交点
也就是1个,选B.
3.【答案】A
解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,
∴猫应该蹲守在△ABC三边垂直平分线的交点处.故选A.
4.【答案】B
解:∵△ABC的三边的垂直平分线交点在△ABC的边上,
∴△ABC的形状为直角三角形.故选B.
5.【答案】D
解:∵AB=AC,D为BC中点,
∴CD=BD,∠BDO=∠CDO=90°,
在△ABD和△ACD中,
,
∴△ABD≌△ACD;
∵EF垂直平分AC,
∴OA=OC,AE=CE,
在△AOE和△COE中,
,
∴△AOE≌△COE;
在△BOD和△COD中,
,
∴△BOD≌△COD;
在△AOC和△AOB中,
,
∴△AOC≌△AOB;
故选D.
6.【答案】到线段两个端点距离相等的点在线段的垂直平分线上,两点确定一条直线
7.【答案】(1)90° (2)30°;4
解:(1)△ABC,△AQB中,AC=AQ,BC=BQ,AB=AB,△ABC≌△ABQ,∠CAB=∠QAB, 根据等腰三角形性质,我们可知:AD是等腰△ACQ底边的高、中线和顶角的平分线. ∴∠ADC=90°. (2)AC=AB,∠ACB=60°, ∴△ABC是等边三角形.CD∥AB, ∴∠ACD=∠BCD=30°.CD=BCsin60°=2. S△ABC=AB·CD÷2=4×2÷2=4.21教育网
8.【答案】D
解:因为PA+PC=BC=PB+PC,所以,PA=PB,点P在AB的垂直平分线上。故选D.
9.【答案】C
解:在直线MN上截取线段h,带有随意性,与作图语言的准确性不相符.故选C.
10.【答案】C
解:∵MN是线段AB的垂直平分线,
∴AD=BD,
∵△ADC的周长为10,AB=7,
∴AC+AD+CD=10,
∴△ABC的周长为:AB+AC+BC=AB+AC+CD+BD=AB+
(AC+CD+AD)=10+7=17.故选C.
11.(1)解:如图①所示.
(2)证明:连接BD,如图②所示.
∵∠C=60°,∠A=40°,∴∠CBA=80°.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠A=∠DBA=40°.
∴∠DBA=∠CBA.
∴BD平分∠CBA.
12.解:(1)∠ADE=90°.
(2)由题意知MN是线段AC的垂直平分线,∴AE=EC.
∴AB+BE+AE=AB+BE+EC=AB+BC=7.
即△ABE的周长为7.
13.证明:连接PA,则PA=PB,
∴∠B=∠PAB=22.5°,∴∠APD=45°.
又∵AD⊥BC,∴PD=AD.
∵AD⊥BC,∴∠DPF+∠PFD=90°.
∵PE⊥AC,∴∠AFE+∠DAC=90°.
又∵∠AFE=∠PFD,∴∠DPF=∠DAC.
在△PDF和△ADC中,
∴△PDF≌△ADC(ASA).∴DF=DC.
14.证明:如图,延长ED至点M,使DM=ED,连接MC,MF,则EF=FM.
∵BD=CD,ED=DM,∠EDB=∠CDM,
∴△BDE≌△CDM(SAS).
∴BE=CM.
∵CF+CM>MF,
∴BE+CF>EF.
第2课时 线段垂直平分线的应用
基础检测
知识点1三角形三边的垂直平分线
1.到三角形三个顶点距离相等的点,是三角形三条边的 的交点,即三角形三条边的垂直平分线交于 .?21世纪教育网版权所有
2.平面内到不在同一条直线上的三个点A,B,C的距离相等的点有( )
A.0个 B.1个 C.2个 D.3个
3.如图,地面上有三个洞口A,B,C,老鼠可以从任意一个洞口跑出,猫为能同时最省力地顾及三个洞口(到A,B,C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )21cnjy.com
A.△ABC三边垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
4.已知△ABC三边的垂直平分线的交点在△ABC的边上,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
5.(2015·泰州)如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
知识点2线段垂直平分线的作图及应用
6.(2015·北京)阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线
已知:线段AB
小芸的作法如下:
如图,(1)分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C,D两点;
(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是?
.?
7.如图,已知线段AB,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点C,Q,连接CQ与AB相交于点D,连接AC,BC.那么:
(1)∠ADC= ;?
(2)当线段AB=4,∠ACB=60°时,∠ACD= ,△ABC的面积等于 .?
8.(2015·深圳)如图,已知△ABC,AB
A.(1) B.(2) C.(3) D.(4)
10.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )2·1·c·n·j·y
A.7 B.14 C.17 D.20
培优检测
题型1作线段垂直平分线在证角平分线中的应用
11.(2015·庆阳)如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图:作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);【来源:21·世纪·教育·网】
(2)求证:BD平分∠CBA.
题型2作线段垂直平分线在求边、角中的应用
12.如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,E,连接AE.21·世纪*教育网
(1)求∠ADE的度数(直接写出结果);
(2)当AB=3,BC=4时,求△ABE的周长.
题型3构造线段垂直平分线的基本图形在证线段 相等中的应用
13.如图,在△ABC中,∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.
14.如图,在△ABC中,D为BC的中点,E,F分别是AB,AC上的点,且DE⊥DF.
求证:BE+CF>EF.
参考答案
1.【答案】垂直平分线;一点
2.【答案】B
解:首先到AB两点距离相等的点,这些点的集合是AB的中垂线
同样,到BC两点距离相等的点的集合是BC的中垂线
那么要ABC都距离相等,就是AB的中垂线与BC中垂线的交点
也就是1个,选B.
3.【答案】A
解:∵三角形三边垂直平分线的交点到三个顶点的距离相等,
∴猫应该蹲守在△ABC三边垂直平分线的交点处.故选A.
4.【答案】B
解:∵△ABC的三边的垂直平分线交点在△ABC的边上,
∴△ABC的形状为直角三角形.故选B.
5.【答案】D
解:∵AB=AC,D为BC中点,
∴CD=BD,∠BDO=∠CDO=90°,
在△ABD和△ACD中,
,
∴△ABD≌△ACD;
∵EF垂直平分AC,
∴OA=OC,AE=CE,
在△AOE和△COE中,
,
∴△AOE≌△COE;
在△BOD和△COD中,
,
∴△BOD≌△COD;
在△AOC和△AOB中,
,
∴△AOC≌△AOB;
故选D.
6.【答案】到线段两个端点距离相等的点在线段的垂直平分线上,两点确定一条直线
7.【答案】(1)90° (2)30°;4
解:(1)△ABC,△AQB中,AC=AQ,BC=BQ,AB=AB,△ABC≌△ABQ,∠CAB=∠QAB, 根据等腰三角形性质,我们可知:AD是等腰△ACQ底边的高、中线和顶角的平分线. ∴∠ADC=90°. (2)AC=AB,∠ACB=60°, ∴△ABC是等边三角形.CD∥AB, ∴∠ACD=∠BCD=30°.CD=BCsin60°=2. S△ABC=AB·CD÷2=4×2÷2=4.21教育网
8.【答案】D
解:因为PA+PC=BC=PB+PC,所以,PA=PB,点P在AB的垂直平分线上。故选D.
9.【答案】C
解:在直线MN上截取线段h,带有随意性,与作图语言的准确性不相符.故选C.
10.【答案】C
解:∵MN是线段AB的垂直平分线,
∴AD=BD,
∵△ADC的周长为10,AB=7,
∴AC+AD+CD=10,
∴△ABC的周长为:AB+AC+BC=AB+AC+CD+BD=AB+
(AC+CD+AD)=10+7=17.故选C.
11.(1)解:如图①所示.
(2)证明:连接BD,如图②所示.
∵∠C=60°,∠A=40°,∴∠CBA=80°.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠A=∠DBA=40°.
∴∠DBA=∠CBA.
∴BD平分∠CBA.
12.解:(1)∠ADE=90°.
(2)由题意知MN是线段AC的垂直平分线,∴AE=EC.
∴AB+BE+AE=AB+BE+EC=AB+BC=7.
即△ABE的周长为7.
13.证明:连接PA,则PA=PB,
∴∠B=∠PAB=22.5°,∴∠APD=45°.
又∵AD⊥BC,∴PD=AD.
∵AD⊥BC,∴∠DPF+∠PFD=90°.
∵PE⊥AC,∴∠AFE+∠DAC=90°.
又∵∠AFE=∠PFD,∴∠DPF=∠DAC.
在△PDF和△ADC中,
∴△PDF≌△ADC(ASA).∴DF=DC.
14.证明:如图,延长ED至点M,使DM=ED,连接MC,MF,则EF=FM.
∵BD=CD,ED=DM,∠EDB=∠CDM,
∴△BDE≌△CDM(SAS).
∴BE=CM.
∵CF+CM>MF,
∴BE+CF>EF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
