第四节 角平分线 课时1同步练习.

第四节角平分线
第1课时 角平分线的性质与判定
基础检测
知识点1角平分线的性质
1.如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是(　　)
A.PC>PD
B.PC=PD
C.PCD.不能确定
2.(2016·莆田)如图,OP是∠AOB的平分线,点C,D分别在角的两边
OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是(　　)
A.PC⊥OA,PD⊥OB
B.OC=OD
C.∠OPC=∠OPD
D.PC=PD
3.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是(　　)21教育网
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
4.(2016·湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(　　)
A.8 B.6 C.4 D.2
5.(中考·威海)如图,在△ABC中,∠ABC=50°,∠ACB=60°,
点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是(　　)21cnjy.com
A.∠BAC=70° B.∠DOC=90°
C.∠BDC=35° D.∠DAC=55°
知识点2角平分线的判定
6.角的内部到角的两边的　　　　相等的点在角的　　　　　上;因此判定角平分线,需要满足两个条件:“　　　　　”和“　　　　　”.其一般思路是:“作垂直,证相等”.?www.21-cn-jy.com
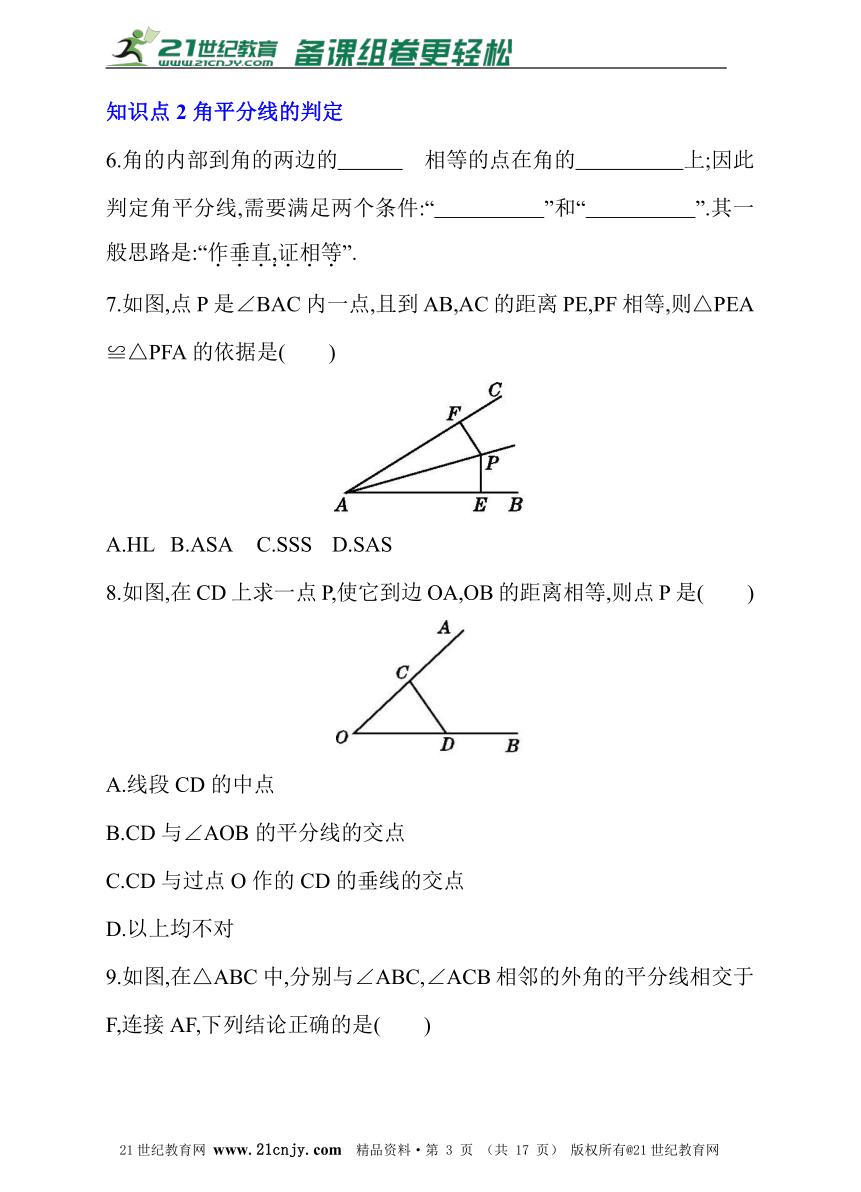
7.如图,点P是∠BAC内一点,且到AB,AC的距离PE,PF相等,则△PEA
≌△PFA的依据是(　　)
A.HL B.ASA C.SSS D.SAS
8.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是(　　)
A.线段CD的中点
B.CD与∠AOB的平分线的交点
C.CD与过点O作的CD的垂线的交点
D.以上均不对
9.如图,在△ABC中,分别与∠ABC,∠ACB相邻的外角的平分线相交于
F,连接AF,下列结论正确的是(　　)
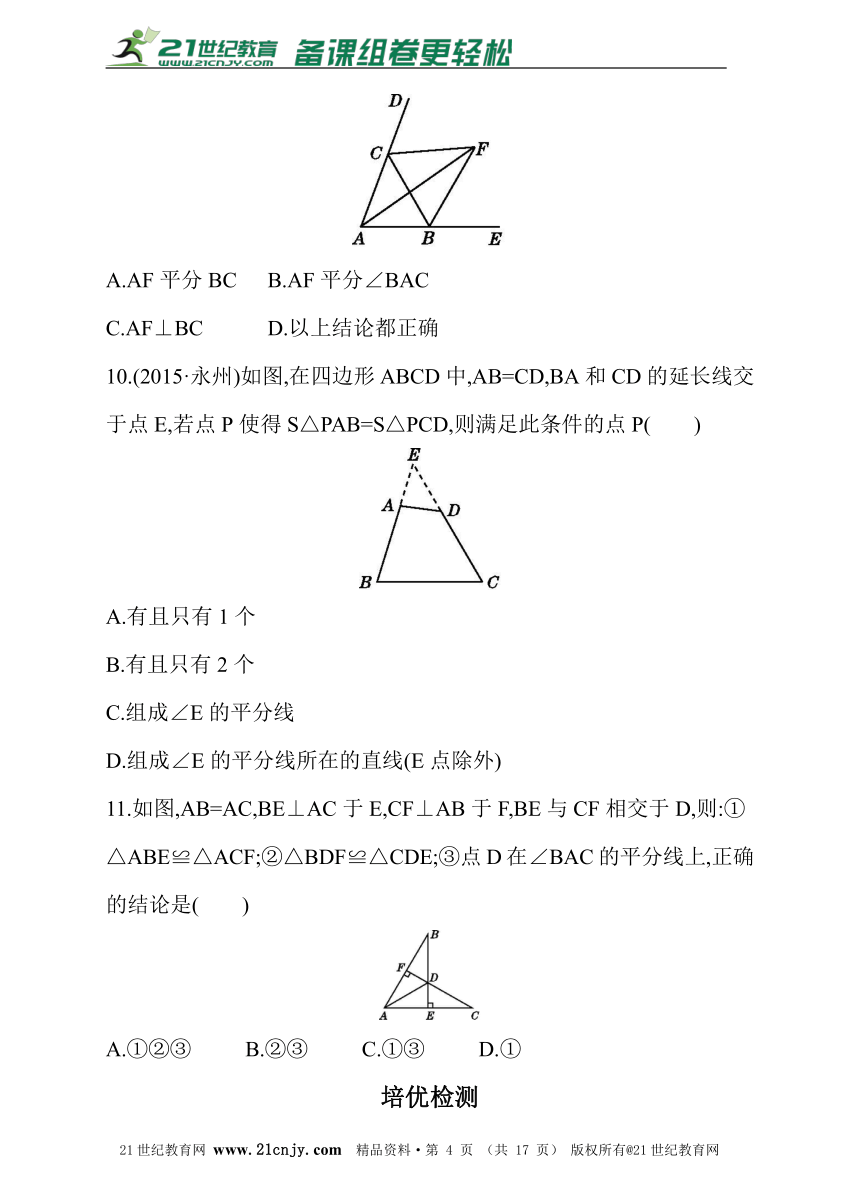
A.AF平分BC B.AF平分∠BAC
C.AF⊥BC D.以上结论都正确
10.(2015·永州)如图,在四边形ABCD中,AB=CD,BA和CD的延长线交
于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P(　　)
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线
D.组成∠E的平分线所在的直线(E点除外)
11.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE与CF相交于D,则:①
△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上,正确
的结论是(　　)
A.①②③　 　B.②③　 　C.①③　 　D.①
培优检测
(一)角平分线性质的应用
题型1角平分线的性质在证线段相等中的应用
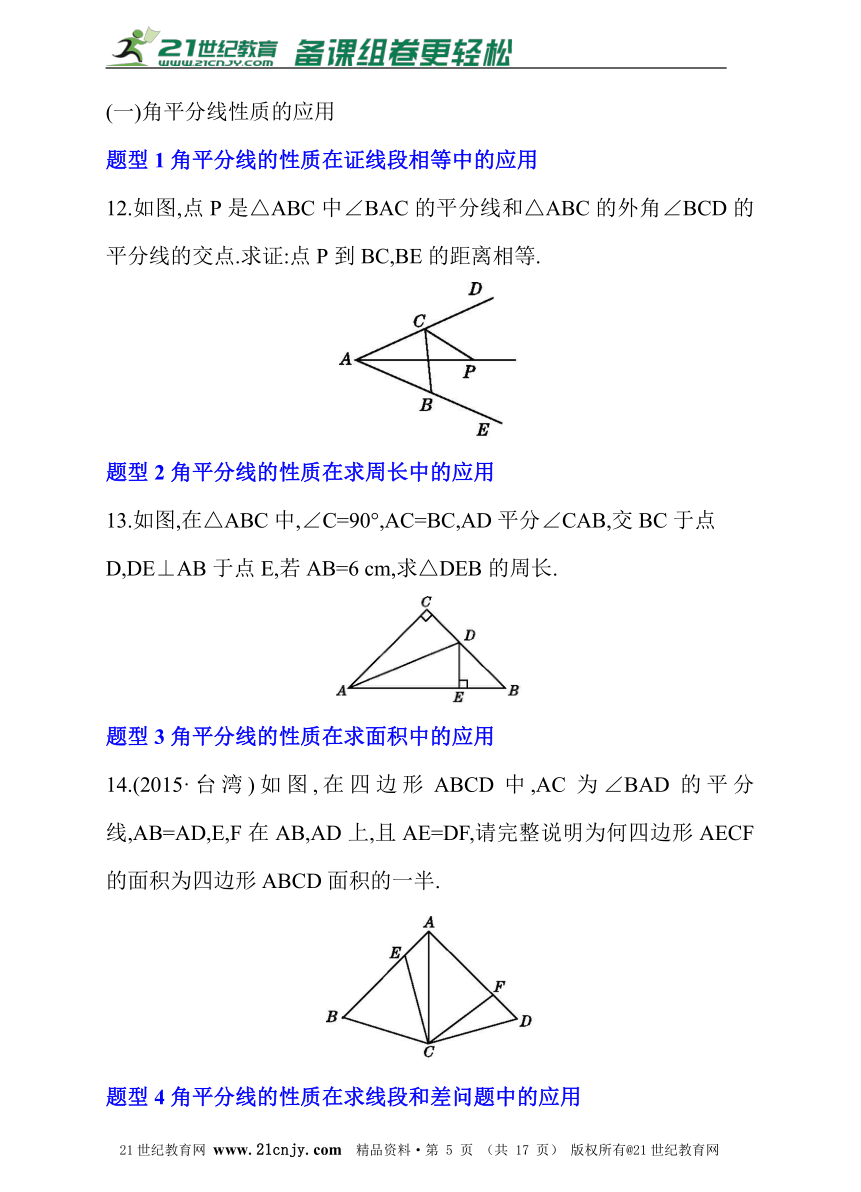
12.如图,点P是△ABC中∠BAC的平分线和△ABC的外角∠BCD的平分线的交点.求证:点P到BC,BE的距离相等.【来源：21·世纪·教育·网】
题型2角平分线的性质在求周长中的应用
13.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若AB=6 cm,求△DEB的周长.21·世纪*教育网
题型3角平分线的性质在求面积中的应用
14.(2015·台湾)如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,E,F在AB,AD上,且AE=DF,请完整说明为何四边形AECF的面积为四边形ABCD面积的一半. www-2-1-cnjy-com
题型4角平分线的性质在求线段和差问题中的应用
15.如图,AE∥CF,AG,CG分别平分∠EAC和∠FCA,过点G的直线BD⊥AE,交AE于B,交CF于D.2-1-c-n-j-y
求证:AB+CD=AC.
16.如图,BC>AB,AD=DC,BD平分∠ABC.
求证:∠BAD+∠C=180°.
(二)角平分线判定的应用
题型1用“作垂直,通过全等证相等”判定角平分线的应用
17.如图,PA=PB,∠1+∠2=180°.
求证:OP平分∠AOB.
题型2用“作垂直,通过等积证相等”判定角平分的应用
18.如图,已知F,G是OA上两点,M,N是OB上两点,且FG=MN,△PFG
和△PMN的面积相等.试判断点P是否在∠AOB的平分线上,并说明理由.
题型3角平分线的判定的实际应用
19.如图,李明计划在张村E、李村F之间建一家超市,张、李两村坐落在两相交公路内.超市的位置应满足下列条件:(1)使其到两公路的距离相等;(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置(简要说明作法).21·cn·jy·com
题型4角平分线的判定和性质的综合应用
20.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.若连接AM,则AM是否平分∠DAB?并说明理由.2·1·c·n·j·y
21.如图,CE⊥AB,BF⊥AC,垂足分别为E,F,BF交CE于点D,BD=CD.
(1)求证:点D在∠BAC的平分线上.
(2)若将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换,成立吗?试说明理由.
参考答案
1.【答案】B
解：利用角的平分线上的点到角的两边的距离相等可知PC=PD，选B.
2.【答案】D
解：A．PC⊥OA，PD⊥OB得出∠PCO=∠PDO=90°，根据AAS判定定理成立，B．OC=OD，根据SAS判定定理成立，C．∠OPC=∠OPD，根据ASA判定定理成立，D．PC=PD，根据SSA无判定定理不成立，故选D．21*cnjy*com
【答案】D
解：∵OP平分∠AOB，PA⊥OA，PB⊥OB
∴PA=PB
∴△OPA≌△OPB
∴∠APO=∠BPO，OA=OB
∴A、B、C项正确
设PO与AB相交于E
∵OA=OB，∠AOP=∠BOP，OE=OE
∴△AOE≌△BOE
∴∠AEO=∠BEO=90°
∴OP垂直AB
而不能得到AB平分OP
故D不成立，故选D．
4.【答案】C
解：过点P作PE⊥BC于E，
∵AB∥CD，PA⊥AB，
∴PD⊥CD，
∵BP和CP分别平分∠ABC和∠DCB，
∴PA=PE，PD=PE，
∴PE=PA=PD，
∵PA+PD=AD=8，
∴PA=PD=4，
∴PE=4.
故选C.
5.【答案】B
解：∵∠ABC=50°，∠ACB=60°，
∴∠BAC=180°-∠ABC-∠ACB=180°-50°-60°=70°，
故A选项正确，
∵BD平分∠ABC，
∴∠ABO=∠ABC=×50°=25°，
在△ABO中，
∠AOB=180°-∠BAC-∠ABO=180°-70°-25°=85°，
∴∠DOC=∠AOB=85°，
故B选项错误；
∵CD平分∠ACE，
∴∠ACD=
（180°-60°）=60°，
∴∠BDC=180°-85°-60°=35°，
故C选项正确；
∵BD、CD分别是∠ABC和∠ACE的平分线，
∴AD是△ABC的外角平分线，
∴∠DAC=
（180°-70°）=55°，
故D选项正确．
故选：B．
6.【答案】距离;平分线;垂直;相等
7.【答案】A
解：∵点P到AB、AC的距离相等，
∴PE=PF，
又∵PA是公共边，
∴△PEA≌△PFA用的是PA=PA，PE=PF，
符合斜边直角边定理，即HL．
故选A．
8.【答案】B
解：利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交P．
故选B．
9.【答案】B
解：解：过F点分别作AB、BC、AC的垂线，垂足分别为E、G、D，
∵∠ABC、∠ACB外角的平分线相交于点F，
∴EF=GF，GF=DF，
∴EF=DF，
∴AF平分∠BAC．
故选B．
10.【答案】D
解：作E的平分线，可得点P到AB和CD的距离相等，因为AB=CD，所以此时点P满足S△PAB=S△PCD，故选D.21世纪教育网版权所有
11.【答案】A
12.证明:过点P作PM⊥AB于M,PN⊥BC于N,PH⊥AC于H,如图所示.
∵AP平分∠BAC,∴PH=PM.
同理,PN=PH.∴PM=PN=PH.
即点P到BC,BE的距离相等.
13.解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE,∠C=∠DEA=90°.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(HL).∴AC=AE.
∵CD=DE,∴BC=CD+DB=DE+DB.
又∵AC=BC,∴AE=AC=DE+DB,
∴DE+DB+BE=AB=6 cm.∴△DEB的周长为6 cm.
14.解:分别过C作CG⊥AB于G,CH⊥AD于H,如图所示.
∵AC为∠BAD的平分线,
∴CG=CH.
∵AB=AD,
∴△ABC的面积=△ACD的面积.
又∵AE=DF,
∴△AEC的面积=△CDF的面积.
∵△BCE的面积=△ABC的面积-△AEC的面积,
△ACF的面积=△ACD的面积-△CDF的面积,
∴△BCE的面积=△ACF的面积.
∵四边形AECF的面积=△AEC的面积+△ACF的面积,
∴四边形AECF的面积=△AEC的面积+△BCE的面积.
∴四边形AECF的面积=△ABC的面积.
∵四边形ABCD的面积=△ABC的面积+△ACD的面积,
∴四边形ABCD的面积=2△ABC的面积.
∴四边形AECF的面积为四边形ABCD面积的一半.
15.证明:过G作GH⊥AC于H,如图所示.
方法一:∵AE∥CF,BD⊥AE交CF于D,∴GD⊥CF.
∵AG,CG分别平分∠EAC和∠FCA,
∴∠BAG=∠GAH,∠GCH=∠GCD.
易得∠BGA=∠HGA,∠HGC=∠DGC.
又由CD⊥GD,CH⊥GH,AH⊥GH,AB⊥GB.
易得CD=CH,AB=AH.
∴AB+CD=AH+CH=AC.
方法二:∵AE∥CF,BD⊥AE交CF于D.∴GD⊥CF,∵AG平分∠EAC,∴BG=HG.
在Rt△AGH和Rt△AGB中,
∴Rt△AGH≌Rt△AGB(HL).
∴AH=AB.同理可得,CD=CH.
∴AB+CD=AH+CH=AC.
16.证明:过点D作DE⊥AB交BA的延长线于点E,作DF⊥BC于F,如图所示.
∵BD平分∠ABC,∴DE=DF.
在Rt△ADE和Rt△CDF中,
∴Rt△ADE≌Rt△CDF(HL).
∴∠EAD=∠C.
∵∠EAD+∠BAD=180°,
∴∠BAD+∠C=180°.
17.证明:过点P作PE⊥AO,PF⊥OB,垂足分别为E,F,则∠AEP=∠BFP=90°.
∵∠1+∠2=180°,∠2+∠PBO=180°,
∴∠1=∠PBO.
在△PAE和△PBF中,
∴△PAE≌△PBF(AAS).∴PE=PF.
∴OP为∠AOB的平分线,即OP平分∠AOB.
18.解:点P在∠AOB的平分线上.理由:如图,过P分别作PD⊥OA于点D,PE⊥OB于点E.
∵S△PFG=FG·PD,
S△PFG=S△PMN,
∴FG·PD=MN·PE.
又∵FG=MN,∴PD=PE.
∴点P在∠AOB的平分线上.
19.解:如图,连接EF,作∠ACB的平分线交EF于点O,则点O就是所要建超市的位置.
20.解:AM平分∠DAB.理由如下:
过点M作ME⊥AD,垂足为E.
∵∠1=∠2,MC⊥CD,ME⊥AD,
∴ME=MC.
∵M是BC的中点,
∴MC=MB.∴ME=MB.
∵MB⊥AB,ME⊥AD,
∴AM平分∠DAB.
21.(1)证明:∵CE⊥AB,BF⊥AC,∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
∴DE=DF.
∴点D在∠BAC的平分线上.
(2)解:将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换仍然成立.理由如下:
∵CE⊥AB,BF⊥AC,
∴∠DEB=∠DFC=90°.
∵点D在∠BAC的平分线上,∴DE=DF.
在△BDE与△CDF中,
∴△BDE≌△CDF(ASA).
∴BD=CD.