第四节 角平分线 课时2同步练习.

第四节角平分线
第2课时 三角形的角平分线
基础检测
知识点1三角形的角平分线
1.三角形的三条内角平分线相交于一点,并且这一点到________相等.?
2.如图,点P为△ABC三条角平分线的交点,PD⊥AB,PE⊥BC,PF⊥AC,则PD________PE________PF.?21·cn·jy·com
3.如图,小林已经画出了一个三角形的两条角平分线,他说:“我不用再将第三个角平分,就能画出第三条角平分线.”他说的有道理吗?他会怎样做?答:　　　　　　　　　　　　　　　　　　.他这样做的理由是什么?答:________.?www.21-cn-jy.com
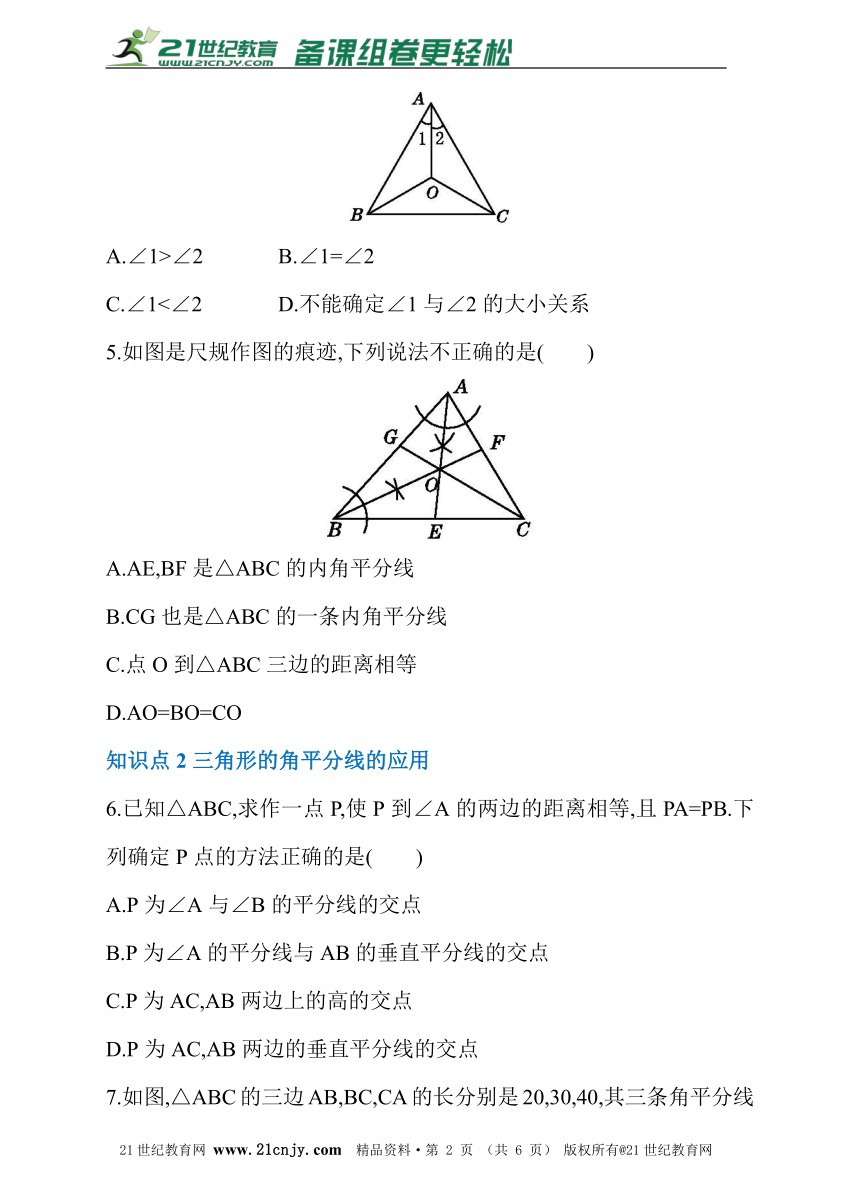
4.如图,在△ABC中,∠ABC,∠ACB的平分线相交于O,下列结论正确的是(　　)
A.∠1>∠2 　　B.∠1=∠2
C.∠1<∠2 　　 D.不能确定∠1与∠2的大小关系
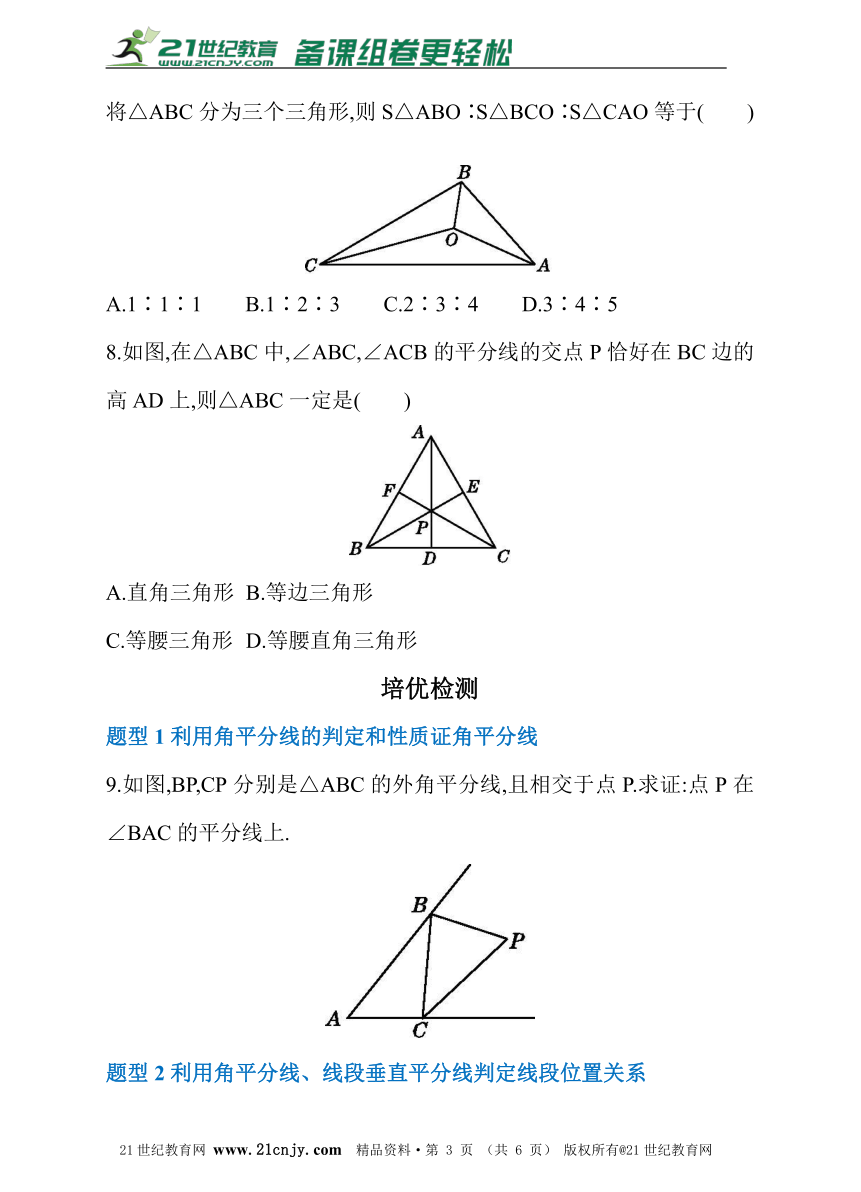
5.如图是尺规作图的痕迹,下列说法不正确的是(　　)
A.AE,BF是△ABC的内角平分线
B.CG也是△ABC的一条内角平分线
C.点O到△ABC三边的距离相等
D.AO=BO=CO
知识点2三角形的角平分线的应用
6.已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是(　　)21·世纪*教育网
A.P为∠A与∠B的平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
7.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于(　　)【来源：21·世纪·教育·网】
A.1∶1∶1　　B.1∶2∶3　　C.2∶3∶4　　D.3∶4∶5
8.如图,在△ABC中,∠ABC,∠ACB的平分线的交点P恰好在BC边的高AD上,则△ABC一定是(　　)www-2-1-cnjy-com
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
培优检测
题型1利用角平分线的判定和性质证角平分线
9.如图,BP,CP分别是△ABC的外角平分线,且相交于点P.求证:点P在∠BAC的平分线上.
题型2利用角平分线、线段垂直平分线判定线段位置关系
10.如图,OE,OF分别是△ABC中AB,AC边的中垂线(即垂直平分线),∠OBC,∠OCB的平分线相交于点I,试判断OI与BC的位置关系,并给出证明.2-1-c-n-j-y
参考答案
1.【答案】三边距离
2.【答案】=;=
解：∵点P为△ABC三条角平分线交点，PD⊥AB，PE⊥BC，
∴PD=PE，
同理可得PD=PF，
∴PD=PE=PF．
3.【答案】有道理.连接CO,并延长交AB于点F,则CF即为∠ACB的平分线;三角形的三条角平分线交于一点21教育网
4.【答案】B
5.【答案】D
解：A、AE、BF是△ABC的内角平分线，此选项正确，不合题意；
B、CG也是△ABC的一条内角平分线，此选项正确，不合题意；
C、点O到△ABC三边的距离相等，此选项正确，不合题意；
D、无法得到AO=BO=CO，此选项错误，符合题意．
故选：D．
6.【答案】B
解：P到∠A两边的距离相等——角平分线推论：角平分线上的点到角两边的距离是相等的。（即p到两边的垂线段长相等）
PA=PB——垂直平分线定理：中垂线上的点到线段两端点的距离相等。 所以答案应为B。
【答案】C
解：利用同高不同底的三角形的面积之比就是底之比可知选C．
故选C．
【答案】C
解：∵∠ABC与∠ACB的平分线的交点P，
∴点P是△ABC的内心，
∴AD是顶角的平分线，
又∵AD是BC上的高，
∴△ADB≌△ADC，
∴AB=AC．
∴△ABC一定是等腰三角形．
故答案为：C.
9.证明:过点P分别作PE⊥AB于E,PF⊥AC于F,PG⊥BC于G.∵BP,CP分别是△ABC的外角平分线,∴PE=PG,PG=PF,则PE=PF.∴点P在∠BAC的平分线上.21世纪教育网版权所有
10.解:OI⊥BC.
证明:如图,连接AO,延长OI交BC于点M.∵OE,OF分别为AB,AC的中垂线,∴OA=OB,OA=OC.∴OB=OC.21cnjy.com
又∵BI,CI分别为∠OBC,∠OCB的平分线,∴点I必在∠BOC的平分线上.∴∠BOI=∠COI.2·1·c·n·j·y
在△BOM和△COM中,
∴△BOM≌△COM(SAS).
∴∠BMO=∠CMO.
又∵∠BMO+∠CMO=180°,
∴∠BMO=∠CMO=90°.∴OI⊥BC.