第二章 第二节 不等式的基本性质同步练习
文档属性
| 名称 | 第二章 第二节 不等式的基本性质同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-09 00:00:00 | ||
图片预览



文档简介
第二节 不等式的基本性质
基础检测
知识点1不等式的基本性质1
1.不等式的基本性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变,即如果a>b,那么a±c b±c.?21cnjy.com
知识点2不等式的基本性质2
2.不等式的基本性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变,即如果a>b,c>0,那么ac bc.?
3.已知实数a,b,若a>b,则下列结论正确的是( )
A.a-5C.< D.3a>3b
4.(2015·乐山)下列说法不一定成立的是( )
A.若a>b,则a+c>b+c
B.若a+c>b+c,则a>b
C.若a>b,则ac2>bc2
D.若ac2>bc2,则a>b
5.(2015·南充)若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n
C.> D.m2>n2
知识点3不等式的基本性质3
6.不等式两边乘(或除以)同一个 数,不等号的方向改变,即如果a>b,c<0,那么ac < bc.?21·cn·jy·com
7.给出下列结论:
①由2a>3,得a>;②由2-a<0,得a>2;
③由a>b,得-3a>-3b;④由a>b,得a-9>b-9.
其中,正确的结论共有( )
A.1个 B.2个 C.3个 D.4个
8.(2015·怀化)下列不等式变形正确的是( )
A.由a>b得ac>bc B.由a>b得-2a>-2b
C.由a>b得-a<-b D.由a>b得a-29.实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c B.a+cC.ac>bc D.<
知识点4不等式的对称性、传递性
10.(1)若a b,则b(2)若a>b,b>c,则a c,即不等式具有同向传递性.?
11.若2x>y,则y 2x(填“>”或“<”).?
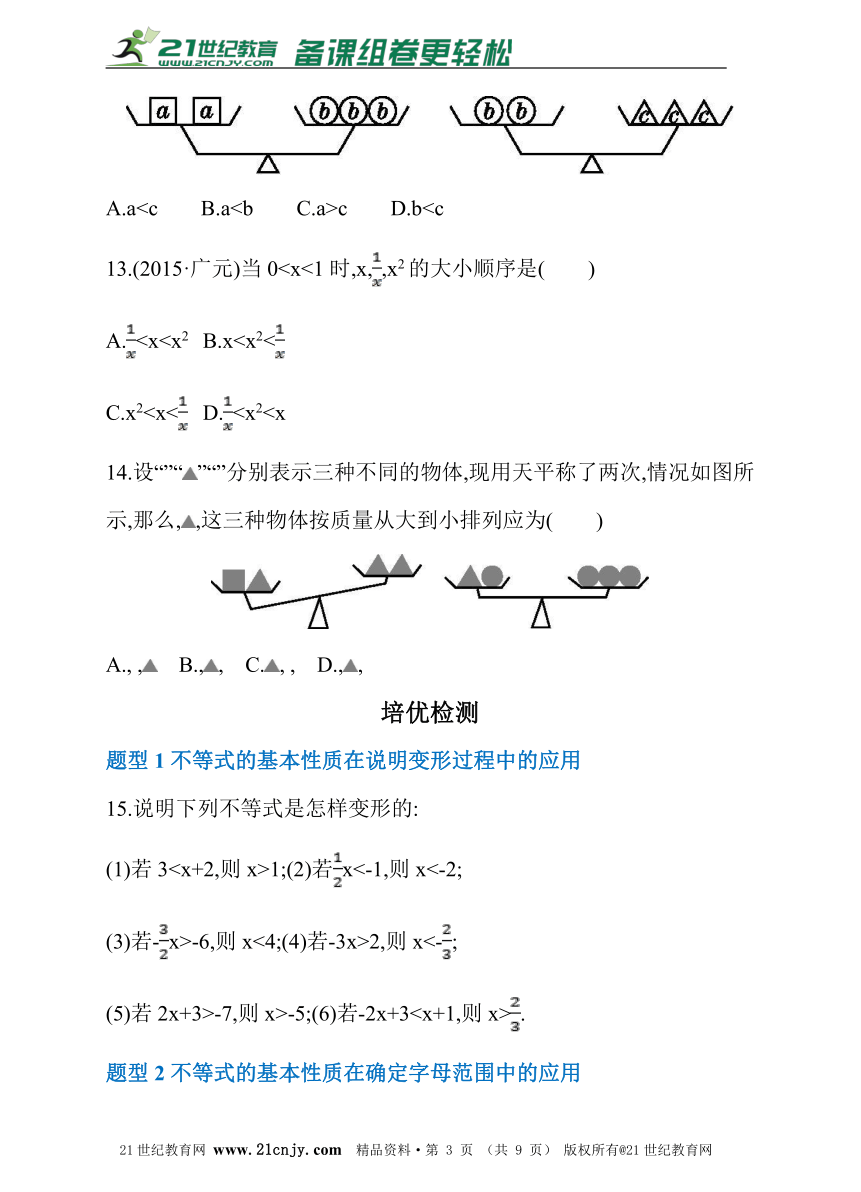
12.如图,a,b,c分别表示三种物体的质量,则下列判断正确的是( )
A.ac D.b13.(2015·广元)当0A.C.x214.设“”“”“”分别表示三种不同的物体,现用天平称了两次,情况如图所示,那么,,这三种物体按质量从大到小排列应为( )
A., , B.,, C., , D.,,
培优检测
题型1不等式的基本性质在说明变形过程中的应用
15.说明下列不等式是怎样变形的:
(1)若31;(2)若x<-1,则x<-2;
(3)若-x>-6,则x<4;(4)若-3x>2,则x<-;
(5)若2x+3>-7,则x>-5;(6)若-2x+3.
题型2不等式的基本性质在确定字母范围中的应用
16.指出下列各式成立的条件:
(1)由mx(2)由amb;
(3)由a>-5,得a2≤-5a;
(4)由3x>4y,得3x-m>4y-m.
题型3不等式的基本性质在化简求值中的应用
已知关于x的不等式(1-a)x>2两边都除以1-a,得x<,试化简:|a-1|+|a+2|.
题型4不等式的基本性质在比较大小中的应用
18.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
(1)若A-B>0,则A B;?
(2)若A-B=0,则A B;?
(3)若A-B<0,则A B.?
这种比较大小的方法称为“作差法”.
请运用这种方法尝试解决下面的问题:
比较4+3a2-2b+b2与3a2-2b+1的大小.
19.现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
(1)利用性质①比较2a与a的大小(a≠0);
(2)利用性质②比较2a与a的大小(a≠0).
参考答案
1.【答案】>
2.【答案】>;>
3.【答案】D
解:A、a>b,则a-5>b-5,选项错误;
B、a>b,则2+a>2+b,选项错误;
C、a>b,则 >,选项错误;
D、正确.故选D.
4.【答案】C
解:A、在不等式a>b的两边同时加上c,不等式仍成立,即a+c>b+c,故本选项错误;
B、在不等式a+c>b+c的两边同时减去c,不等式仍成立,即a>b,故本选项错误;
C、当c=0时,若a>b,则不等式ac2>bc2不成立,故本选项正确;
D、在不等式ac2>bc2的两边同时除以不为0的c2,该不等式仍成立,即a>b,故本选项错误.
故选:C.
5.【答案】D
解:当0>m>n时,不等式的两边都乘以负数,不等号的方向改变,故D错误。选D。
6.【答案】负;<
7.【答案】C
解:∵2a>3,
∴不等式的两边都除以2得:a>,∴(1)正确;
∵2-a<0,
∴-a<-2,
∴a>2,∴(2)正确;
∵a>b,
∴不等式的两边都乘以-3得:-3a<-3b,∴(3)错误;
∵a>b,
∴a-9>b-9,∴(4)正确;
即正确的有3个,
故选C.
8.【答案】B
解:根据不等式的基本性质分别进行判定即可得出答案.
A.由a>b,得ac>bc,当c<0,不等号的方向改变.故此选项错误;
B.由a>b,得-2a<-2b,不等式两边乘以同一个负数,不等号的方向改变,故此选项正确;
C.由a>b,得-a>-b,不等式两边乘(或除以)同一个负数,不等号的方向改变;故此选项错误;
D.由a>b,得a-2<b-2,不等式两边同时减去一个数,不等号方向不改变,故此选项错误.
故选B.
9.【答案】B
解:先根据数轴的特征可得 所以,,,.
10.【答案】(1)> (2)>
11.【答案】<
12.【答案】C
解:∵2a=3b,
∴a>b,
∵2b>3c,
∴b>c,
∴a>b>c.
故答案选C.
13.【答案】C
解:∵0<x<1,
令x=,那么x2=,
=4,
∴x2<x<
故选C
14.【答案】B
解:设▲、●、■的质量为a、b、c,
由图形可得:
由①得:c>a,
由②得:a=2b,
故可得c>a>b.
故选B.
15.解:(1)31;
(2)x<-1,两边乘2,得x<-2;
(3)-x>-6,两边除以-,得x<4;
(4)-3x>2,两边除以-3,得x<-;
(5)2x+3>-7,两边减去3,再除以2,得x>-5;
(6)-2x+3.
16.解:(1)m>0;(2)m<0;(3)-5(4)m为任意实数.
17.解:由已知得1-a<0,即a>1.
则|a-1|+|a+2|=a-1+a+2=2a+1.
18.解:(1)> (2)= (3)<
(4+3a2-2b+b2)-(3a2-2b+1)=b2+3>0,故4+3a2-2b+b2>3a2-2b+1.
19.解:(1)当a>0时,在a>0两边同时加上a,得a+a>a+0,即2a>a;当a<0时,在a<0两边同时加上a,得a+a(2)当a>0时,由2>1,得2·a>1·a,即2a>a;当a<0时,由2>1,得2·a<1·a,即2a
基础检测
知识点1不等式的基本性质1
1.不等式的基本性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变,即如果a>b,那么a±c b±c.?21cnjy.com
知识点2不等式的基本性质2
2.不等式的基本性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变,即如果a>b,c>0,那么ac bc.?
3.已知实数a,b,若a>b,则下列结论正确的是( )
A.a-5
4.(2015·乐山)下列说法不一定成立的是( )
A.若a>b,则a+c>b+c
B.若a+c>b+c,则a>b
C.若a>b,则ac2>bc2
D.若ac2>bc2,则a>b
5.(2015·南充)若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n
C.> D.m2>n2
知识点3不等式的基本性质3
6.不等式两边乘(或除以)同一个 数,不等号的方向改变,即如果a>b,c<0,那么ac < bc.?21·cn·jy·com
7.给出下列结论:
①由2a>3,得a>;②由2-a<0,得a>2;
③由a>b,得-3a>-3b;④由a>b,得a-9>b-9.
其中,正确的结论共有( )
A.1个 B.2个 C.3个 D.4个
8.(2015·怀化)下列不等式变形正确的是( )
A.由a>b得ac>bc B.由a>b得-2a>-2b
C.由a>b得-a<-b D.由a>b得a-2
A.a-c>b-c B.a+c
知识点4不等式的对称性、传递性
10.(1)若a b,则b
11.若2x>y,则y 2x(填“>”或“<”).?
12.如图,a,b,c分别表示三种物体的质量,则下列判断正确的是( )
A.a
A., , B.,, C., , D.,,
培优检测
题型1不等式的基本性质在说明变形过程中的应用
15.说明下列不等式是怎样变形的:
(1)若3
(3)若-x>-6,则x<4;(4)若-3x>2,则x<-;
(5)若2x+3>-7,则x>-5;(6)若-2x+3
题型2不等式的基本性质在确定字母范围中的应用
16.指出下列各式成立的条件:
(1)由mx
(3)由a>-5,得a2≤-5a;
(4)由3x>4y,得3x-m>4y-m.
题型3不等式的基本性质在化简求值中的应用
已知关于x的不等式(1-a)x>2两边都除以1-a,得x<,试化简:|a-1|+|a+2|.
题型4不等式的基本性质在比较大小中的应用
18.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
(1)若A-B>0,则A B;?
(2)若A-B=0,则A B;?
(3)若A-B<0,则A B.?
这种比较大小的方法称为“作差法”.
请运用这种方法尝试解决下面的问题:
比较4+3a2-2b+b2与3a2-2b+1的大小.
19.现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
(1)利用性质①比较2a与a的大小(a≠0);
(2)利用性质②比较2a与a的大小(a≠0).
参考答案
1.【答案】>
2.【答案】>;>
3.【答案】D
解:A、a>b,则a-5>b-5,选项错误;
B、a>b,则2+a>2+b,选项错误;
C、a>b,则 >,选项错误;
D、正确.故选D.
4.【答案】C
解:A、在不等式a>b的两边同时加上c,不等式仍成立,即a+c>b+c,故本选项错误;
B、在不等式a+c>b+c的两边同时减去c,不等式仍成立,即a>b,故本选项错误;
C、当c=0时,若a>b,则不等式ac2>bc2不成立,故本选项正确;
D、在不等式ac2>bc2的两边同时除以不为0的c2,该不等式仍成立,即a>b,故本选项错误.
故选:C.
5.【答案】D
解:当0>m>n时,不等式的两边都乘以负数,不等号的方向改变,故D错误。选D。
6.【答案】负;<
7.【答案】C
解:∵2a>3,
∴不等式的两边都除以2得:a>,∴(1)正确;
∵2-a<0,
∴-a<-2,
∴a>2,∴(2)正确;
∵a>b,
∴不等式的两边都乘以-3得:-3a<-3b,∴(3)错误;
∵a>b,
∴a-9>b-9,∴(4)正确;
即正确的有3个,
故选C.
8.【答案】B
解:根据不等式的基本性质分别进行判定即可得出答案.
A.由a>b,得ac>bc,当c<0,不等号的方向改变.故此选项错误;
B.由a>b,得-2a<-2b,不等式两边乘以同一个负数,不等号的方向改变,故此选项正确;
C.由a>b,得-a>-b,不等式两边乘(或除以)同一个负数,不等号的方向改变;故此选项错误;
D.由a>b,得a-2<b-2,不等式两边同时减去一个数,不等号方向不改变,故此选项错误.
故选B.
9.【答案】B
解:先根据数轴的特征可得 所以,,,.
10.【答案】(1)> (2)>
11.【答案】<
12.【答案】C
解:∵2a=3b,
∴a>b,
∵2b>3c,
∴b>c,
∴a>b>c.
故答案选C.
13.【答案】C
解:∵0<x<1,
令x=,那么x2=,
=4,
∴x2<x<
故选C
14.【答案】B
解:设▲、●、■的质量为a、b、c,
由图形可得:
由①得:c>a,
由②得:a=2b,
故可得c>a>b.
故选B.
15.解:(1)3
(2)x<-1,两边乘2,得x<-2;
(3)-x>-6,两边除以-,得x<4;
(4)-3x>2,两边除以-3,得x<-;
(5)2x+3>-7,两边减去3,再除以2,得x>-5;
(6)-2x+3
16.解:(1)m>0;(2)m<0;(3)-5
17.解:由已知得1-a<0,即a>1.
则|a-1|+|a+2|=a-1+a+2=2a+1.
18.解:(1)> (2)= (3)<
(4+3a2-2b+b2)-(3a2-2b+1)=b2+3>0,故4+3a2-2b+b2>3a2-2b+1.
19.解:(1)当a>0时,在a>0两边同时加上a,得a+a>a+0,即2a>a;当a<0时,在a<0两边同时加上a,得a+a
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
