18.2.1 矩形同步练习

18.2.1 矩形
一、单选题（共8题；共24分）
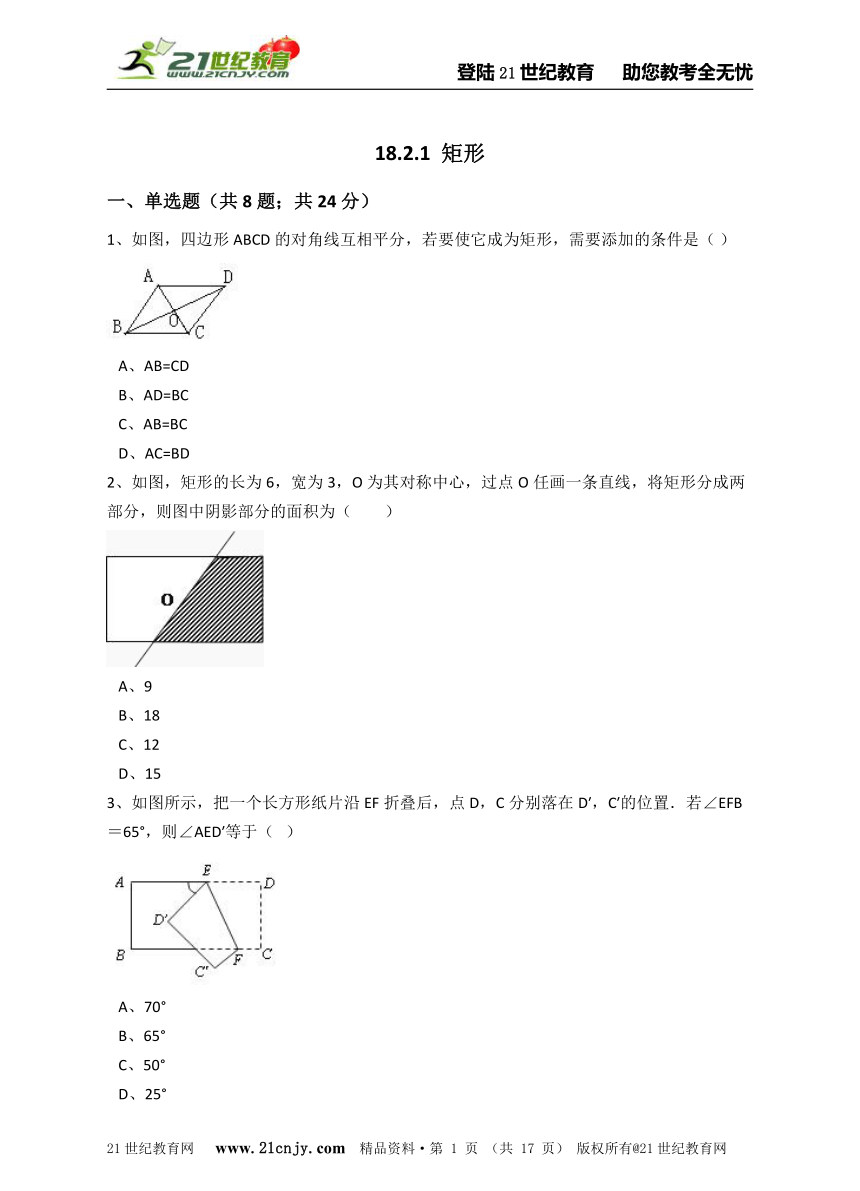
1、如图，四边形ABCD的对角线互相平分，若要使它成为矩形，需要添加的条件是（?）
A、AB=CDB、AD=BCC、AB=BCD、AC=BD
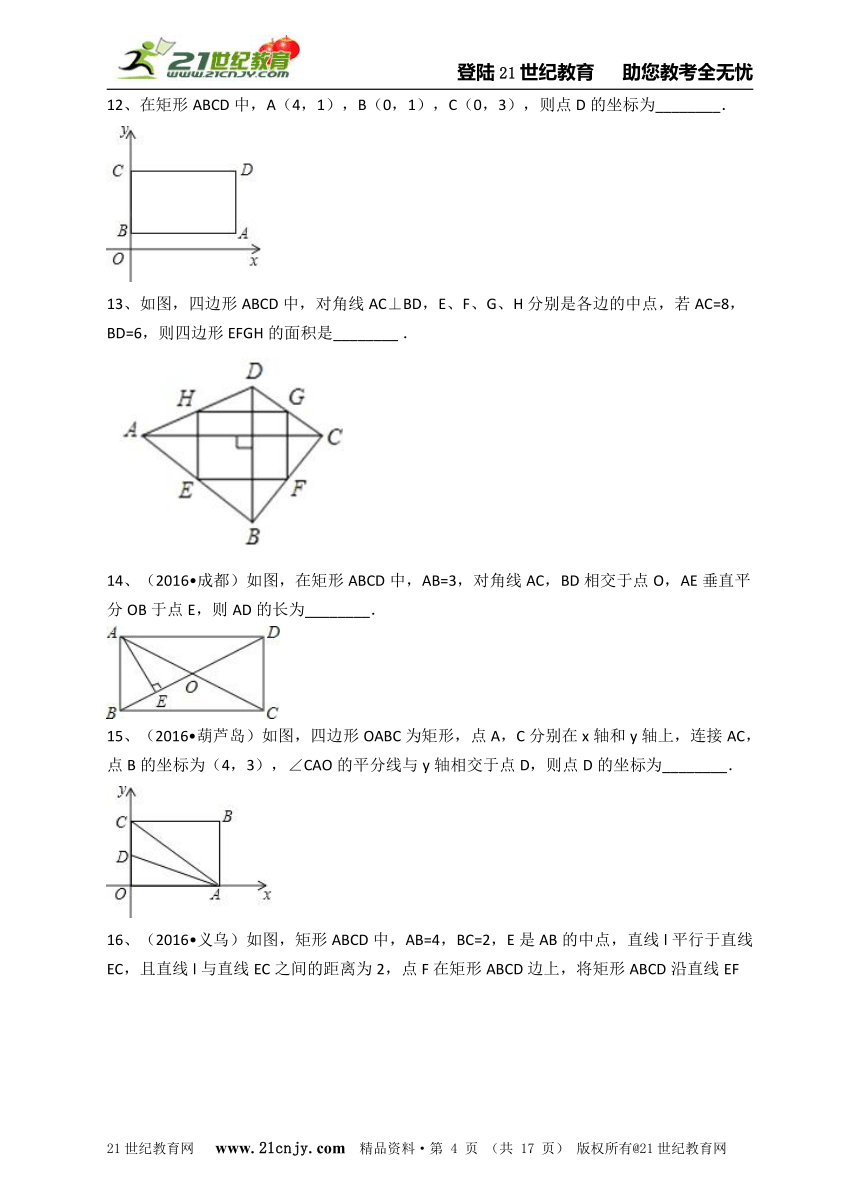
2、如图，矩形的长为6，宽为3，O为其对称中心，过点O任画一条直线，将矩形分成两部分，则图中阴影部分的面积为（　　）www.21-cn-jy.com
A、9B、18C、12D、15
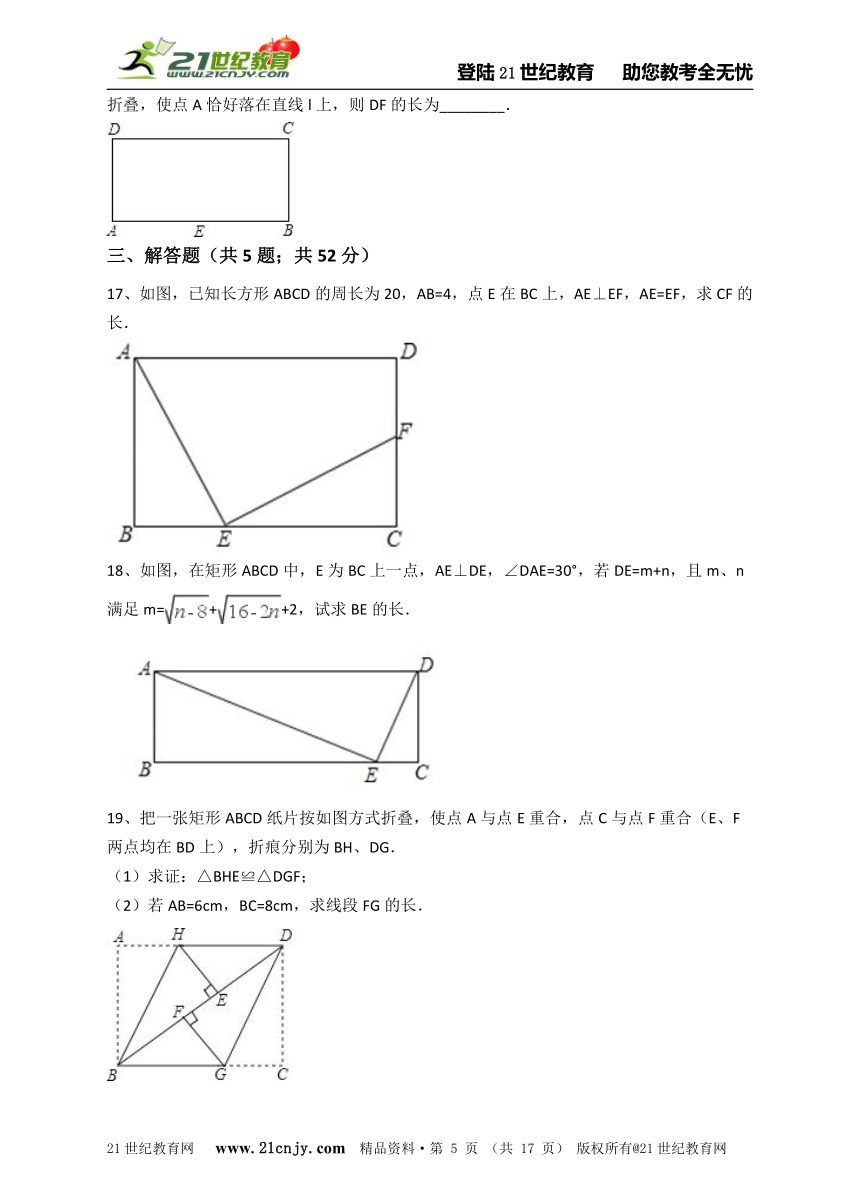
3、如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′等于（???）
A、70°B、65°C、50°D、25°
4、△ABC中，AB=AC=5，BC=6，点D是BC上的一点，那么点D到AB与AC的距离的和为（　　） 21世纪教育网版权所有
A、5B、6C、4D、
5、如图，在Rt△ABC中，∠A＝90°，P为边BC上一动点，PE⊥AB于E ， PF⊥AC于F ， 动点P从点B出发，沿着BC匀速向终点C运动，则线段EF的值大小变化情况是（　　）.
A、一直增大B、一直减小C、先减小后增大D、先增大后减少
6、如图，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AB＝2，则矩形的对角线AC的长是（　　）
A、2B、4C、D、
7、（2016?葫芦岛）如图，在△ABC中，点D，E分别是边AB，AC的中点，AF⊥BC，垂足为点F，∠ADE=30°，DF=4，则BF的长为（? ）
A、4B、8C、2 D、4
8、一次数学课上，老师请同学们在一张长为18厘米，宽为16厘米的矩形纸板上，剪下一个腰长为10厘米的等腰三角形，且要求等腰三角形的一个顶点与矩形的一个顶点重合，其它两个顶点在矩形的边上，则剪下的等腰三角形的面积为多少平方厘米（　　）
A、50B、50或40C、50或40或30D、50或30或20
二、填空题（共8题；共24分）
9、如图所示，已知平行四边形ABCD ， 下列条件：①AC＝BD ， ②AB＝AD ， ③∠1＝∠2，④AB⊥BC中，能说明平行四边形ABCD是矩形的有（填写序号）________? ． 21*cnjy*com
10、在矩形ABCD中，对角线AC ， BD相交于点O ， 若对角线AC＝10cm，边BC＝8cm，则△ABO的周长为________．
11、（2015?宿迁）如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为?________
12、在矩形ABCD中，A（4，1），B（0，1），C（0，3），则点D的坐标为________．
13、如图，四边形ABCD中，对角线AC⊥BD，E、F、G、H分别是各边的中点，若AC=8，BD=6，则四边形EFGH的面积是________?．?
14、（2016?成都）如图，在矩形ABCD中，AB=3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为________．21·世纪*教育网
15、（2016?葫芦岛）如图，四边形OABC为矩形，点A，C分别在x轴和y轴上，连接AC，点B的坐标为（4，3），∠CAO的平分线与y轴相交于点D，则点D的坐标为________．
16、（2016?义乌）如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为________．21教育名师原创作品
三、解答题（共5题；共52分）
17、如图，已知长方形ABCD的周长为20，AB=4，点E在BC上，AE⊥EF，AE=EF，求CF的长．?
18、如图，在矩形ABCD中，E为BC上一点，AE⊥DE，∠DAE=30°，若DE=m+n，且m、n满足m=++2，试求BE的长．
19、把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG．（1）求证：△BHE≌△DGF；（2）若AB=6cm，BC=8cm，求线段FG的长．【来源：21·世纪·教育·网】
20、已知：如图，BE、BF分别是∠ABC与它的邻补角∠ABD的平分线，AE⊥BE，垂足为点E，AF⊥BF，垂足为点F，EF分别交边AB、AC于点M和N．求证：（1）四边形AFBE是矩形；（2）MN=BC．?21教育网
21、如图，在△ABC中，O是AC上的一个动点（不与点A、C重合），过O点作直线MN//BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。（1）试说明：OE=OF。（2）当O点运动到何处时，四边形AECF是矩形？并证明你的结论。

18.2.1 矩形
参考答案
一、单选题
2、【答案】A 【解析】【分析】矩形是中心对称图形．根据中心对称图形的性质易知阴影面积是矩形面积的一半．21·cn·jy·com
【解答】因为O为矩形的对称中心，则阴影部分的面积等于矩形面积的一半．因为矩形的面积为18，所以其面积为9．故选A．【来源：21cnj*y.co*m】
3、【答案】C 【解析】【分析】已知∠EFB=65°，欲求∠AED′，可通过折叠的性质，结合三角形内角和定理求解。根据折叠的性质，折叠前后角相等，即∠DEF=∠FED′，又根据AD∥BC，得∠DEF=∠EFB，因此∠DEF=∠FED′=65°，则∠AED′=180°-65°-65°=50°．故选C． 21*cnjy*com
4、【答案】D 【解析】【分析】作△ABC的高CQ，AH，过C作CZ⊥DE交ED的延长线于Z， ∵AB=AC=5，BC=6，AH⊥BC，∴BH=CH=3，根据勾股定理得：AH=4，根据三角形的面积公式得：BC?AH=AB?CQ，即：6×4=5CQ，解得：CQ=，∵CQ⊥AB，DE⊥AB，CZ⊥DE，∴∠CQE=∠QEZ=∠Z=90°，∴四边形QEZC是矩形，∴CQ=ZE，∵∠QEZ=∠Z=90°，∴∠QEZ+∠Z=180°，∴CZ∥AB，∴∠B=∠ZCB，∵DF⊥AC，CZ⊥DE，∴∠Z=∠DFC=90°，∵AB=AC，∴∠B=∠ACB，∴∠ACB=∠ZCB，∵CD=CD，∠ACB=∠ZCB，∴△ZCD≌△FCD，∴DF=DZ，∴DE+DF=CQ=．故选D． www-2-1-cnjy-com
5、【答案】C 【解析】【解答】如图下图所示，连接AP ， ∵∠A＝90°，PE⊥AB ， PF⊥AC ， ∴四边形AFPE是矩形，∴EF＝AP ， 由垂线段最短可得AP⊥BC时，AP最短，则线段EF的值最小，∴动点P从点B出发，沿着BC匀速向终点C运动，则线段EF的值大小变化情况是先减小后增大；故选C． 【分析】连接CP ， 先判断出四边形CFPE是矩形，根据矩形的对角线相等可得EF＝CP ， 再根据垂线段最短可得CP⊥AB时，线段EF的值最小，即可判断出动点P从点B出发，沿着BC匀速向终点C运动，线段EF的值大小变化情况． 【版权所有：21教育】
6、【答案】B 【解析】【解答】因为在矩形ABCD中，所以AO＝AC＝ BD＝BO，又因为∠AOB＝60°，所以△AOB是等边三角形，所以AO＝AB＝2，所以AC＝2AO＝4．故选B．【分析】本题的关键是利用等边三角形和矩形对角线的性质求长度．本题难度中等，考查矩形的性质．
【分析】先利用直角三角形斜边中线性质求出AB，再在RT△ABF中，利用30角所对的直角边等于斜边的一半，求出AF即可解决问题．本题考查三角形中位线性质、含30度角的直角三角形性质、直角三角形斜边中线性质、勾股定理等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．
8、【答案】C 【解析】【解答】如图四边形ABCD是矩形，AD＝18cm，AB＝16cm；本题可分三种情况：①如图（1）：△AEF中，AE＝AF＝10cm；S△AEF＝?AE?AF＝50cm2； ②如图（2）：△AGH中，AG＝GH＝10cm；在Rt△BGH中，BG＝AB﹣AG＝16﹣10＝6cm；根据勾股定理有：BH＝8cm；∴S△AGH＝ AG?BH＝ ×8×10＝40cm2；③如图（3）：△AMN中，AM＝MN＝10cm；在Rt△DMN中，MD＝AD﹣AM＝18﹣10＝8cm；根据勾股定理有DN＝6cm；∴S△AMN＝ AM?DN＝ ×10×6＝30cm2 ． 故选C．【分析】本题中由于等腰三角形的位置不确定，因此要分三种情况进行讨论求解，①如图（1），②如图（2），③如图（3），分别求得三角形的面积．题主要考查了等腰三角形的性质.矩形的性质.勾股定理等知识，解题的关键在于能够进行正确的讨论．
二、填空题
9、【答案】①④ 【解析】【解答】能说明平行四边形ABCD是矩形的有：①对角线相等的平行四边形是矩形；④有一个角是直角的平行四边形是矩形．【分析】矩形是特殊的平行四边形，矩形有而平行四边形没有的特征是：矩形的四个内角是直角；矩形的对角线相等且互相平分；可根据这些特点来选择条件．
10、【答案】16cm 【解析】【解答】在矩形ABCD中，对角线AC ， BD相交于点O ， 对角线AC＝10cm，∴∠ABC＝90°，OA＝OB＝ AC＝5cm，∵BC＝8cm，∴AB＝ cm，∴△ABO的周长为：OA＋OB＋AB＝16cm． 【分析】根据勾股定理求出边AB的长度是本题的解题关键．
11、【答案】5 【解析】【解答】∵△ABC是直角三角形，CD是斜边的中线，∴CD=AB，又∵EF是△ABC的中位线，∴AB=2CD=2×5=10cm，∴EF=?×10=5cm．故答案为：5．【分析】已知CD是Rt△ABC斜边AB的中线，那么AB=2CD；EF是△ABC的中位线，则EF应等于AB的一半．
12、【答案】（4，3） 【解析】【解答】因为AB＝4，BC＝2，则AD＝BC＝2，CD＝AB＝4．∴D的坐标为（4，3）．故答案为：（4，3）．【分析】画出草图，根据A，B，C的位置与矩形的性质来确定出D的位置．此题主要考查学生对坐标的特点及矩形的性质的掌握情况．
13、【答案】12 【解析】【解答】解：∵E、F、G、H分别是四边形ABCD各边的中点，∴EH∥BD且EH=BD，FG∥BD且=BD，∴EH∥FG，EH=FG，同理EF∥HG，EF=HG，又∵AC⊥BD，∴四边形EFGH是矩形，∴四边形EFGH=EF×EH=AC×BD=×8××6=12．【分析】根据E、F、G、H分别是各边的中点，利用三角形中位线定理求出EH和EF，判定四边形EFGH是矩形，然后即可四边形EFGH的面积．
14、【答案】3 【解析】【解答】解：∵四边形ABCD是矩形，∴OB=OD，OA=OC，AC=BD，∴OA=OB，∵AE垂直平分OB，∴AB=AO，∴OA=AB=OB=3，∴BD=2OB=6，∴AD= =3 ；故答案为：3 ．【分析】由矩形的性质和线段垂直平分线的性质证出OA=AB=OB=3，得出BD=2OB=6，由勾股定理求出AD即可．此题考查了矩形的性质、等边三角形的判定与性质、线段垂直平分线的性质、勾股定理；熟练掌握矩形的性质，证明三角形是等边三角形是解决问题的关键．
15、【答案】（0， ） 【解析】【解答】解：过D作DE⊥AC于E， ∵四边形ABCO是矩形，B（4，3），∴OC=AB=3，OA=BC=4，∠CCOA=90°，∵AD平分∠OAC，∴OD=DE，由勾股定理得：OA2=AD2﹣OD2 ， AE2=AD2﹣DE2 ， ∴OA=AE=4，由勾股定理得：AC= =5，在Rt△DEC中，DE2+EC2=CD2 ， 即OD2+（5﹣4）2=（3﹣OD）2 ， 解得：OD= ，所以D的坐标为（0， ），故答案为：（0， ）．【分析】过D作DE⊥AC于E，根据矩形的性质和B的坐标求出OC=AB=3，OA=BC=4，∠CCOA=90°，求出OD=DE，根据勾股定理求出OA=AE=4，AC=5，在Rt△DEC中，根据勾股定理得出DE2+EC2=CD2 ， 求出OD，即可得出答案．本题考查了矩形的性质，角平分线性质，勾股定理的应用，能根据勾股定理得出关于OD的方程是解此题的关键．
16、【答案】2 或4﹣2 【解析】【解答】解：如图，当直线l在直线CE上方时，连接DE交直线l于M，∵四边形ABCD是矩形，∴∠A=∠B=90°，AD=BC，∵AB=4，AD=BC=2，∴AD=AE=EB=BC=2，∴△ADE、△ECB是等腰直角三角形，∴∠AED=∠BEC=45°，∴∠DEC=90°，∵l∥EC，∴ED⊥l，∴EM=2=AE，∴点A、点M关于直线EF对称，∵∠MDF=∠MFD=45°，∴DM=MF=DE﹣EM=2 ﹣2，∴DF= DM=4﹣2 ．当直线l在直线EC下方时，∵∠DEF1=∠BEF1=∠DF1E，∴DF1=DE=2 ，综上所述DF的长为2 或4﹣2 ．故答案为2 或4﹣2 ． 【分析】本题考查翻折变换、矩形的性质、等腰直角三角形的性质和判定，解题的关键是正确画出图形，注意有两种情形，属于中考常考题型．当直线l在直线CE上方时，连接DE交直线l于M，只要证明△DFM是等腰直角三角形即可利用DF= DM解决问题，当直线l在直线EC下方时，由∠DEF1=∠BEF1=∠DF1E，得到DF1=DE，由此即可解决问题．
三、解答题
17、【答案】解：∵四边形ABCD是矩形，∴∠B=∠C=90°，∵EF⊥AE，∴∠AEF=90°，∴∠AEB+∠BAE=90°，∠AEB+∠CEF=90°，∴∠BAE=∠CEF，在△ABE和△ECF中，?，∴△ABE≌△ECF，∴AB=CE=4，∵矩形的周长为20，∴BC=6，∴CF=BE=BC﹣CE=BC﹣AB=2．? 【解析】【分析】易证△ADE≌△BEF，推出AE=CE=4，根据矩形周长求出BC=6，则CF=BE=BC﹣CE=BC﹣AB=2，问题得解． 21cnjy.com
18、【答案】解：∵m、n满足m=++2，∴，∴n=8，∴m=2，∵DE=m+n，∴DE=10，∵AE⊥DE，∠DAE=30°，∴AD=2DE=20，∠ADE=60°，∵四边形ABCD是矩形，∴∠ADC=90°，BC=AD=20，∴∠CDE=30°，∴CE=DE=5，∴BE=BC﹣CE=20﹣5=15． 【解析】【分析】根据二次根式的意义求出m、n，得出DE，再由含30°角的直角三角形的性质得出AD，由矩形的性质得出∠ADC=90°，BC=AD=20，得出∠CDE=30°，求出CE，即可得出BE的长． 2-1-c-n-j-y
19、【答案】（1）证明：∵四边形ABCD是矩形，∴AB=CD，∠A=∠C=90°，∠ABD=∠BDC，∵△BEH是△BAH翻折而成，∴∠ABH=∠EBH，∠A=∠HEB=90°，AB=BE，∵△DGF是△DGC翻折而成，∴∠FDG=∠CDG，∠C=∠DFG=90°，CD=DF，∴∠DBH=∠ABD，∠BDG=∠BDC，∴∠DBH=∠BDG，∴△BEH与△DFG中，∠HEB=∠DFG，BE=DF，∠DBH=∠BDG，∴△BEH≌△DFG，（2）解：∵四边形ABCD是矩形，AB=6cm，BC=8cm，∴AB=CD=6cm，AD=BC=8cm，∴BD===10，∵由（1）知，FD=CD，CG=FG，∴BF=10-6=4cm，设FG=x，则BG=8-x，在Rt△BGF中，BG2=BF2+FG2 ， 即（8-x）2=42+x2 ， 解得x=3，即FG=3cm． 【解析】【分析】（1）先根据矩形的性质得出∠ABD=∠BDC，再由图形折叠的性质得出∠ABH=∠EBH，∠FDG=∠CDG，∠A=∠HEB=90°，∠C=∠DFG=90°，进而可得出△BEH≌△DFG；（2）先根据勾股定理得出BD的长，进而得出BF的长，由图形翻折变换的性质得出CG=FG，设FG=x，则BG=8-x，再利用勾股定理即可求出x的值． 2·1·c·n·j·y
20、【答案】证明：（1）∵BE、BF分别是△ABC中∠B及它的外角的平分线，∴∠1=∠2，∠3=∠4，∵∠1+∠2+∠3+∠4=180°，∴∠2+∠3=90°，∵AE⊥BE，E为垂足，AF⊥BF，F为垂足，∴∠AFB=∠AEB=90°，∴四边形AEBF为矩形；（2）∵四边形AEBF为矩形，∴BM=MA=ME，∴∠2=∠5，∵∠2=∠1，∴∠1=∠5，∴ME∥BC，∵M是AB的中点，∴N为AC的中点，∴MN=BC．? 【解析】【分析】（1）由BE、BE是角平分线可得∠EBF是90°，进而由条件中的两个垂直可得两个直角，可得四边形AEBF是矩形；（2）由矩形的F质可得∠2=∠5进而利用角平分线的性质可得∠1=∠5，可得ME∥BC，进而可得N为AC中点，根据三角形中位线性质求出即可． 【出处：21教育名师】