第二章 第五节 一元一次不等式与一次函数同步练习
文档属性
| 名称 | 第二章 第五节 一元一次不等式与一次函数同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 440.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-09 09:02:08 | ||
图片预览


文档简介
第五节 一元一次不等式与一次函数
基础检测
知识点1一次函数与一元一次方程
1.一元一次方程kx+b=0(k,b为常数,k≠0)的解即为函数y=______的图象与______的交点的______坐标;反之函数y=kx+b(k,b为常数,k≠0)的图象与______的交点的______坐标即为方程kx+b=0的解.?
2.直线y=-2x+10与x轴的交点坐标是______,则方程-2x+10=0的解是______.?21·世纪*教育网
3.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2 B.y=2 C.x=-1 D.y=-1
4.一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0) B.(3,0) C.(a,0) D.(-b,0)
5.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( )
6.下列说法错误的是( )
A.方程7x+=0的解,就是直线y=7x+与x轴交点的横坐标
B.方程2x+3=4x+7的解,就是直线y=2x+3与直线y=4x+7交点的横坐标
C.方程7x+=0的解,就是一次函数y=7x+当函数值为0时自变量的值
D.方程7x+=0的解,就是直线y=7x+与y轴交点的纵坐标
知识点2一次函数与一元一次不等式
7.一次函数与一元一次不等式的关系:一元一次不等式kx+b>0(或kx+b<0)的解集,就是一次函数______的图象在x轴 (或______)相应的自变量x的取值范围.?www-2-1-cnjy-com
8.已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x______时,y≤0.?2-1-c-n-j-y
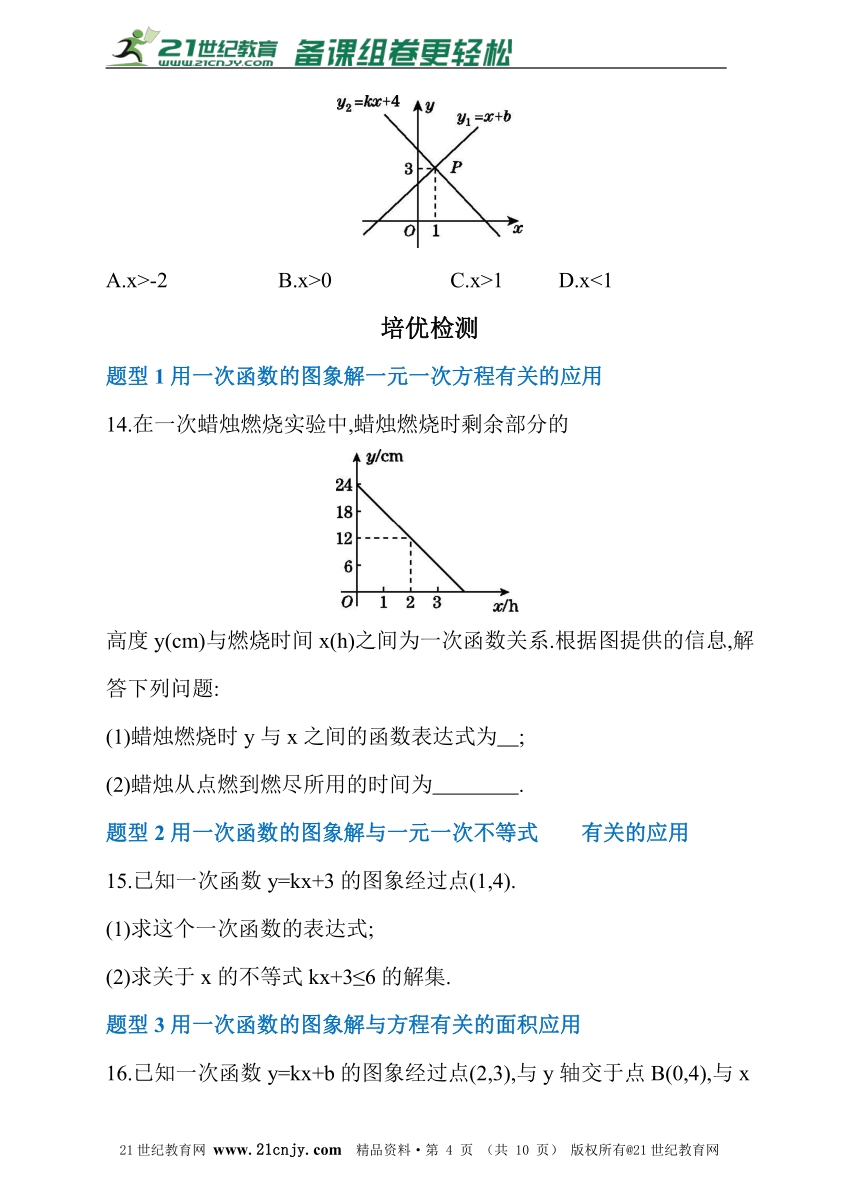
9.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-210.如图,函数y=ax-1的图象过点(1,2),则不等式ax-1>2的解集是( )
A.x<1 B.x>1 C.x<2 D.x>2
11.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式x>kx+b>-2的解集为( )【来源:21cnj*y.co*m】
A.x<2 B.x>-1
C.x<1或x>2 D.-112.若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
A.x<2 B.x>2 C.x<5 D.x>5
13.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )【出处:21教育名师】
A.x>-2 B.x>0 C.x>1 D.x<1
培优检测
题型1用一次函数的图象解一元一次方程有关的应用
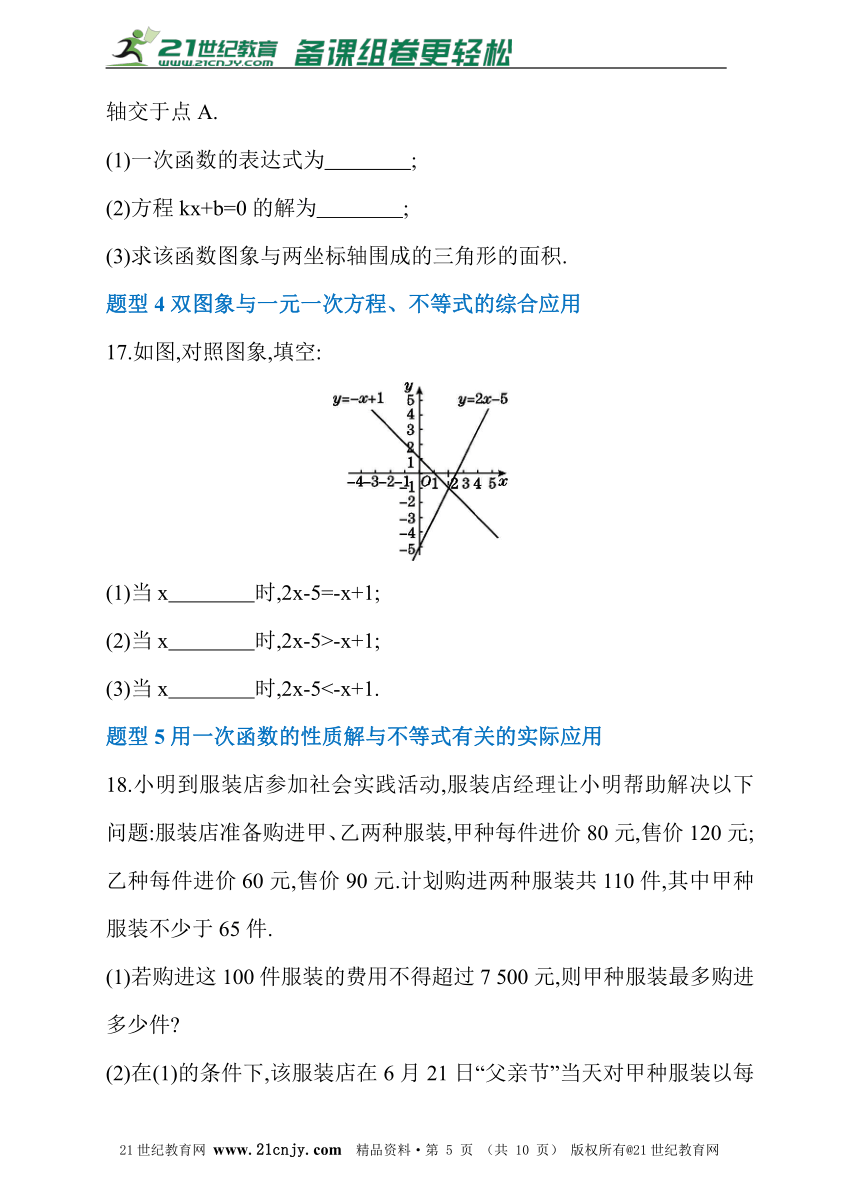
14.在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的
高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图提供的信息,解答下列问题:
(1)蜡烛燃烧时y与x之间的函数表达式为 ;?
(2)蜡烛从点燃到燃尽所用的时间为 .?
题型2用一次函数的图象解与一元一次不等式 有关的应用
15.已知一次函数y=kx+3的图象经过点(1,4).
(1)求这个一次函数的表达式;
(2)求关于x的不等式kx+3≤6的解集.
题型3用一次函数的图象解与方程有关的面积应用
16.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(1)一次函数的表达式为 ;?
(2)方程kx+b=0的解为 ;?
(3)求该函数图象与两坐标轴围成的三角形的面积.
题型4双图象与一元一次方程、不等式的综合应用
17.如图,对照图象,填空:
(1)当x 时,2x-5=-x+1;?
(2)当x 时,2x-5>-x+1;?
(3)当x 时,2x-5<-x+1.?
题型5用一次函数的性质解与不等式有关的实际应用
18.小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共110件,其中甲种服装不少于65件. 21教育网
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店在6月21日“父亲节”当天对甲种服装以每件优惠a(0题型6用一次函数与方程、不等式关系解设计方 案的应用
19.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球.乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店:每买1副球拍赠送1盒乒乓球;乙店:按定价的9折优惠.某班级需购球拍4副、乒乓球若干盒(不少于4盒),请你用学过的知识说明怎样选购合算.
参考答案
1.【答案】kx+b;x轴;横;x轴;横
2.【答案】(5,0);x=5
3.【答案】C
解:kx+b=0
即原函数取y=0代入
看图
当y=0时
x=-1
即方程kx+b=0的解为x=-1
4.【答案】B
解:∵一元一次方程ax-b=0的解x=3,
∴函数y=ax-b的图象与x轴的交点坐标为(3,0),
故选:B.
5.【答案】C
解:∵方程kx+b=0的解是x=3,∴y=kx+b经过点(3,0).故选C.
6.【答案】D
7.【答案】y=kx+b;上方;下方
8.【答案】≥2
解:解:∵一次函数y=kx+b的图象经过两点A(0,1),B(2,0), ∴,解得: 这个一次函数的表达式为y=﹣x+1.解不等式﹣x+1≤0, 解得x≥2. 21·cn·jy·com
9.【答案】-110.【答案】B
解:方法一∵把(1,2)代入y=ax-1得:2=a-1,
解得:a=3,
∴y=3x-1>2,
解得:x>1,
方法二:根据图象可知:y=ax-1>2的x的范围是x>1,
即不等式ax-1>2的解集是x>1,
故答案为B.
11.【答案】D
解:由题意可得方程组,
解得.
一次函数的解析式为:y=x﹣1;
不等式x>kx+b>﹣2即x>x﹣1>﹣2,
可化为,
解得:﹣1<x<2.故选D.
12.【答案】C
解:解:∵一次函数y=kx﹣b经过点(2,0),
∴2k﹣b=0,b=2k.
函数值y随x的增大而减小,则k<0;
解关于k(x﹣3)﹣b>0,
移项得:kx>3k+b,即kx>5k;
两边同时除以k,因为k<0,因而解集是x<5.
故选C.
13.【答案】C
解:解:当x>1时,x+b>kx+4,
即不等式x+b>kx+4的解集为x>1.
故选:C.
14.【答案】(1)y=-6x+24 (2)4 h
15.解:(1)把点(1,4)的坐标代入y=kx+3,得4=k+3,解得k=1,所以这个一次函数的表达式为y=x+3.21世纪教育网版权所有
(2)因为k=1,所以x+3≤6,解得x≤3,即不等式kx+3≤6的解集为x≤3.
16.解:(1)y=-x+4
(2)x=8
(3)S△AOB=×4×8=16.
17.(1)=2 (2)>2 (3)<2
(2)由图象可知,当x>2时,直线y=2x-5落在直线y=-x+1的上方,即2x-5>-x+1.
(3)由图象可知,当x<2时,直线y=2x-5落在直线y=-x+1的下方,即2x-5<-x+1.
18.解:(1)设购进甲种服装x件,由题意可知
80x+60(100-x)≤7 500,解得x≤75.
答:甲种服装最多购进75件.
(2)设总利润为w元,因为甲种服装不少于65件,所以65≤x≤75,且x取正整数.
w=(40-a)x+30(100-x)=(10-a)x+3 000.
方案一:当00,w随x的增大而增大,
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件;
方案二:当a=10时,所有方案获利相同,所以按哪种方案进货都可以;
方案三:当1019.解:设购买x盒乒乓球(x≥4),到甲店购买的付款数为y甲元,到乙店购买的付款数为y乙元.由题意,得www.21-cn-jy.com
y甲=20×4+5(x-4)(x≥4),
y乙=0.9(20×4+5x)(x≥4).
(1)当y甲=y乙时,则20×4+5(x-4)=0.9(20×4+5x),解得x=24;
(2)当y甲(3)当y甲>y乙时,则20×4+5(x-4)>0.9(20×4+5x),解得x>24.
答:当购买乒乓球24盒时,两家商店一样;当购买乒乓球大于或等于4盒并且小于24盒时,去甲店购买合算;当购买乒乓球超过24盒时,去乙店购买合算.【来源:21·世纪·教育·网】
基础检测
知识点1一次函数与一元一次方程
1.一元一次方程kx+b=0(k,b为常数,k≠0)的解即为函数y=______的图象与______的交点的______坐标;反之函数y=kx+b(k,b为常数,k≠0)的图象与______的交点的______坐标即为方程kx+b=0的解.?
2.直线y=-2x+10与x轴的交点坐标是______,则方程-2x+10=0的解是______.?21·世纪*教育网
3.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为( )
A.x=2 B.y=2 C.x=-1 D.y=-1
4.一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0) B.(3,0) C.(a,0) D.(-b,0)
5.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( )
6.下列说法错误的是( )
A.方程7x+=0的解,就是直线y=7x+与x轴交点的横坐标
B.方程2x+3=4x+7的解,就是直线y=2x+3与直线y=4x+7交点的横坐标
C.方程7x+=0的解,就是一次函数y=7x+当函数值为0时自变量的值
D.方程7x+=0的解,就是直线y=7x+与y轴交点的纵坐标
知识点2一次函数与一元一次不等式
7.一次函数与一元一次不等式的关系:一元一次不等式kx+b>0(或kx+b<0)的解集,就是一次函数______的图象在x轴 (或______)相应的自变量x的取值范围.?www-2-1-cnjy-com
8.已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x______时,y≤0.?2-1-c-n-j-y
9.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2
A.x<1 B.x>1 C.x<2 D.x>2
11.如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式x>kx+b>-2的解集为( )【来源:21cnj*y.co*m】
A.x<2 B.x>-1
C.x<1或x>2 D.-1
A.x<2 B.x>2 C.x<5 D.x>5
13.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )【出处:21教育名师】
A.x>-2 B.x>0 C.x>1 D.x<1
培优检测
题型1用一次函数的图象解一元一次方程有关的应用
14.在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的
高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图提供的信息,解答下列问题:
(1)蜡烛燃烧时y与x之间的函数表达式为 ;?
(2)蜡烛从点燃到燃尽所用的时间为 .?
题型2用一次函数的图象解与一元一次不等式 有关的应用
15.已知一次函数y=kx+3的图象经过点(1,4).
(1)求这个一次函数的表达式;
(2)求关于x的不等式kx+3≤6的解集.
题型3用一次函数的图象解与方程有关的面积应用
16.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.
(1)一次函数的表达式为 ;?
(2)方程kx+b=0的解为 ;?
(3)求该函数图象与两坐标轴围成的三角形的面积.
题型4双图象与一元一次方程、不等式的综合应用
17.如图,对照图象,填空:
(1)当x 时,2x-5=-x+1;?
(2)当x 时,2x-5>-x+1;?
(3)当x 时,2x-5<-x+1.?
题型5用一次函数的性质解与不等式有关的实际应用
18.小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共110件,其中甲种服装不少于65件. 21教育网
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店在6月21日“父亲节”当天对甲种服装以每件优惠a(0
19.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球.乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店:每买1副球拍赠送1盒乒乓球;乙店:按定价的9折优惠.某班级需购球拍4副、乒乓球若干盒(不少于4盒),请你用学过的知识说明怎样选购合算.
参考答案
1.【答案】kx+b;x轴;横;x轴;横
2.【答案】(5,0);x=5
3.【答案】C
解:kx+b=0
即原函数取y=0代入
看图
当y=0时
x=-1
即方程kx+b=0的解为x=-1
4.【答案】B
解:∵一元一次方程ax-b=0的解x=3,
∴函数y=ax-b的图象与x轴的交点坐标为(3,0),
故选:B.
5.【答案】C
解:∵方程kx+b=0的解是x=3,∴y=kx+b经过点(3,0).故选C.
6.【答案】D
7.【答案】y=kx+b;上方;下方
8.【答案】≥2
解:解:∵一次函数y=kx+b的图象经过两点A(0,1),B(2,0), ∴,解得: 这个一次函数的表达式为y=﹣x+1.解不等式﹣x+1≤0, 解得x≥2. 21·cn·jy·com
9.【答案】-1
解:方法一∵把(1,2)代入y=ax-1得:2=a-1,
解得:a=3,
∴y=3x-1>2,
解得:x>1,
方法二:根据图象可知:y=ax-1>2的x的范围是x>1,
即不等式ax-1>2的解集是x>1,
故答案为B.
11.【答案】D
解:由题意可得方程组,
解得.
一次函数的解析式为:y=x﹣1;
不等式x>kx+b>﹣2即x>x﹣1>﹣2,
可化为,
解得:﹣1<x<2.故选D.
12.【答案】C
解:解:∵一次函数y=kx﹣b经过点(2,0),
∴2k﹣b=0,b=2k.
函数值y随x的增大而减小,则k<0;
解关于k(x﹣3)﹣b>0,
移项得:kx>3k+b,即kx>5k;
两边同时除以k,因为k<0,因而解集是x<5.
故选C.
13.【答案】C
解:解:当x>1时,x+b>kx+4,
即不等式x+b>kx+4的解集为x>1.
故选:C.
14.【答案】(1)y=-6x+24 (2)4 h
15.解:(1)把点(1,4)的坐标代入y=kx+3,得4=k+3,解得k=1,所以这个一次函数的表达式为y=x+3.21世纪教育网版权所有
(2)因为k=1,所以x+3≤6,解得x≤3,即不等式kx+3≤6的解集为x≤3.
16.解:(1)y=-x+4
(2)x=8
(3)S△AOB=×4×8=16.
17.(1)=2 (2)>2 (3)<2
(2)由图象可知,当x>2时,直线y=2x-5落在直线y=-x+1的上方,即2x-5>-x+1.
(3)由图象可知,当x<2时,直线y=2x-5落在直线y=-x+1的下方,即2x-5<-x+1.
18.解:(1)设购进甲种服装x件,由题意可知
80x+60(100-x)≤7 500,解得x≤75.
答:甲种服装最多购进75件.
(2)设总利润为w元,因为甲种服装不少于65件,所以65≤x≤75,且x取正整数.
w=(40-a)x+30(100-x)=(10-a)x+3 000.
方案一:当0
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件;
方案二:当a=10时,所有方案获利相同,所以按哪种方案进货都可以;
方案三:当10
y甲=20×4+5(x-4)(x≥4),
y乙=0.9(20×4+5x)(x≥4).
(1)当y甲=y乙时,则20×4+5(x-4)=0.9(20×4+5x),解得x=24;
(2)当y甲
答:当购买乒乓球24盒时,两家商店一样;当购买乒乓球大于或等于4盒并且小于24盒时,去甲店购买合算;当购买乒乓球超过24盒时,去乙店购买合算.【来源:21·世纪·教育·网】
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
