3.2 提公因式法 课件
图片预览






文档简介
课件19张PPT。3.2 提公因式法讨 论问题1:630能被哪些数整除?说说你是怎样想的?问题2:a=101,b=99时,求a2 – b2 的值.运用前面所学的知识填空:把下列多项式写 成乘积的形式(1) ma+mb+mc=( )( )
(2) x2 -1 =( )( )
(3) a2 +2ab+b2 =( )2(1) m(a+b+c)=
(2) (x+1)(x-1)=
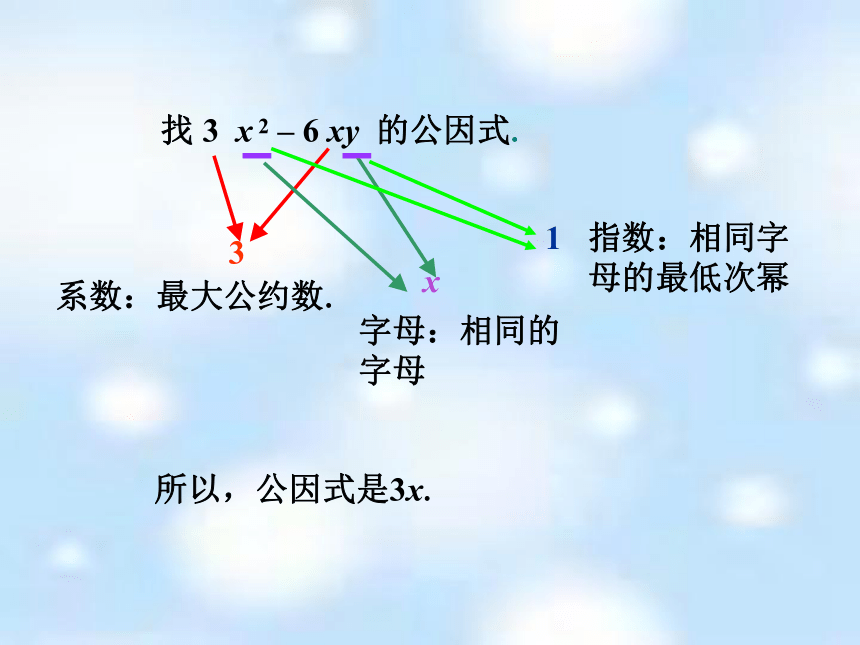
(3) (a+b)2 =ma+mb+mcx2 -1a2 +2ab+b2m a+b+cx+1 x-1a+b 多项式中各项都含有的相同因式,叫做这个多项式的公因式.相同因式m这个多项式有什么特点?找 3 x 2 – 6 xy 的公因式.系数:最大公约数.3字母:相同的字母x 所以,公因式是3x.指数:相同字母的最低次幂1提公因式法 分解因式 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.正确找出多项式各项公因式的关键是:1、定系数:公因式的系数是多项式各项系数的最大公约数.
2、定字母: 字母取多项式各项中都含有的相同的字母.
3、定指数: 相同字母的指数取各项中最小的一个,即字母最低次幂 例1 把5x2-3xy+x因式分解 .分析 多项式各项均含有x,因此公因式为x.第3项将x提出后,括号内的因式为1.解 5x2-3xy+x
= x(5x-3y+1).例2 把4x2 -6x因式分解.分析 先确定公因式的系数,再确定字母. 这两项的系数为4,6,它们的最大公约数是2;两项的字母部分x2与x都含有字母x,且x的最低次数是1,因此公因式为2x.解 4x2 - 6x
= 2x(2x-3) 例3 把8x2y4-12xy2z因式分解. 分析 公因式的系数是8 与12的最大公约数4;公因式含的字母是各项中相同的字母x 和y,它们的指数取各项中次数最低的,因此公因式为4xy2 .解 8x2y4-12xy2z
= (4xy2)·2xy2-(4xy2)·3z
= 4xy2(2xy2-3z).找一找: 下列各多项式的公因式是什么? (3)(a)(a2)(2(m+n))(3mn)(-2xy)(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)4 (m+n) 2 +2(m+n)
(5)9 m 2n-6mn
(6)-6 x 2 y-8 xy 2 (1) 8a3b2 + 12ab3c把下列各式分解因式 分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.(2) 2a(b+c) - 3(b+c)注意:公因式既可以是一个单项式的形式,也可
以是一个多项式的形式整体思想是数学中一种重要而且常用的思想方法.例4 把下列多项式因式分解.(1) x( x -2) – 3(x-2) ;(2)x(x -2)-3( 2-x) .解 x(x-2)-3(x-2)= (x-2)(x-3)(1) x( x -2) – 3(x-2) ;(2)x(x -2)-3( 2-x) .= x(x-2)-3[-(x-2)]解 x(x -2)-3( 2-x) = x( x-2)+3(x-2)= (x-2)(x+3). 例5 把 (a+c)(a-b)2-(a-c)(b-a)2因式分解.解 ( a+c)(a-b)2-(a-c)(b-a)2= (a+c)(a-b)2 -(a-c)(a-b)2= (a-b)2[(a+c)-(a-c)]= (a-b)2(a+c-a+c) = 2c(a-b)2例6 把12xy2(x+y)-18x2y(x+y) 因式分解. 解 12xy2(x+y)- 18x2y(x+y)= 6xy(x+y)(2y-3x).小华解的有误吗?提出负号时括号里的项没变号.诊断注意:首项有负常提负.正确解:原式= - (x2-xy+xz)
=- x(x-y+z)(1) 13.8×0.125+86.2×1/8(2)已知a+b=5,ab=3,求a2b+ab2的值. 解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100
=12.5.解: a2b+ab2 =ab(a+b)=3 × 5=15.巧妙计算
提公因式法分解因式正确的找出多项式各项的公因式.注意:1 多项式是几项,提公因式后也剩几项.
2 当多项式的某一项和公因式相同时提公 因式后剩余的项是1.
3 当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号.课堂小结
(2) x2 -1 =( )( )
(3) a2 +2ab+b2 =( )2(1) m(a+b+c)=
(2) (x+1)(x-1)=
(3) (a+b)2 =ma+mb+mcx2 -1a2 +2ab+b2m a+b+cx+1 x-1a+b 多项式中各项都含有的相同因式,叫做这个多项式的公因式.相同因式m这个多项式有什么特点?找 3 x 2 – 6 xy 的公因式.系数:最大公约数.3字母:相同的字母x 所以,公因式是3x.指数:相同字母的最低次幂1提公因式法 分解因式 如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.正确找出多项式各项公因式的关键是:1、定系数:公因式的系数是多项式各项系数的最大公约数.
2、定字母: 字母取多项式各项中都含有的相同的字母.
3、定指数: 相同字母的指数取各项中最小的一个,即字母最低次幂 例1 把5x2-3xy+x因式分解 .分析 多项式各项均含有x,因此公因式为x.第3项将x提出后,括号内的因式为1.解 5x2-3xy+x
= x(5x-3y+1).例2 把4x2 -6x因式分解.分析 先确定公因式的系数,再确定字母. 这两项的系数为4,6,它们的最大公约数是2;两项的字母部分x2与x都含有字母x,且x的最低次数是1,因此公因式为2x.解 4x2 - 6x
= 2x(2x-3) 例3 把8x2y4-12xy2z因式分解. 分析 公因式的系数是8 与12的最大公约数4;公因式含的字母是各项中相同的字母x 和y,它们的指数取各项中次数最低的,因此公因式为4xy2 .解 8x2y4-12xy2z
= (4xy2)·2xy2-(4xy2)·3z
= 4xy2(2xy2-3z).找一找: 下列各多项式的公因式是什么? (3)(a)(a2)(2(m+n))(3mn)(-2xy)(1) 3x+6y
(2)ab-2ac
(3) a 2 - a 3
(4)4 (m+n) 2 +2(m+n)
(5)9 m 2n-6mn
(6)-6 x 2 y-8 xy 2 (1) 8a3b2 + 12ab3c把下列各式分解因式 分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.(2) 2a(b+c) - 3(b+c)注意:公因式既可以是一个单项式的形式,也可
以是一个多项式的形式整体思想是数学中一种重要而且常用的思想方法.例4 把下列多项式因式分解.(1) x( x -2) – 3(x-2) ;(2)x(x -2)-3( 2-x) .解 x(x-2)-3(x-2)= (x-2)(x-3)(1) x( x -2) – 3(x-2) ;(2)x(x -2)-3( 2-x) .= x(x-2)-3[-(x-2)]解 x(x -2)-3( 2-x) = x( x-2)+3(x-2)= (x-2)(x+3). 例5 把 (a+c)(a-b)2-(a-c)(b-a)2因式分解.解 ( a+c)(a-b)2-(a-c)(b-a)2= (a+c)(a-b)2 -(a-c)(a-b)2= (a-b)2[(a+c)-(a-c)]= (a-b)2(a+c-a+c) = 2c(a-b)2例6 把12xy2(x+y)-18x2y(x+y) 因式分解. 解 12xy2(x+y)- 18x2y(x+y)= 6xy(x+y)(2y-3x).小华解的有误吗?提出负号时括号里的项没变号.诊断注意:首项有负常提负.正确解:原式= - (x2-xy+xz)
=- x(x-y+z)(1) 13.8×0.125+86.2×1/8(2)已知a+b=5,ab=3,求a2b+ab2的值. 解:原式=13.8×0.125+86.2×0.125
=0.125×(13.8+86.2)
=0.125×100
=12.5.解: a2b+ab2 =ab(a+b)=3 × 5=15.巧妙计算
提公因式法分解因式正确的找出多项式各项的公因式.注意:1 多项式是几项,提公因式后也剩几项.
2 当多项式的某一项和公因式相同时提公 因式后剩余的项是1.
3 当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号.课堂小结
