4.4 平行线的判定 课件
图片预览






文档简介
课件24张PPT。4.4 平行线的判定学习目标1、掌握平行线的三种判定方法.并会运
用所学方法来判断两条直线是否平行.
2、会根据判定方法进行简单的推理并学
会用数学符号写出简单的推理过程.
3、体会数学中的转化思想.重点:
1.了解平行线的定义,并能用符号表示.能借助三角板,方格纸等画平行线.
2.探索平行线的基本性质(基本事实).
难点:探索平行线的基本判定方法. 复习提问(1)平面内两条直线的位置关系有几种?(2)怎样过已知直线外一点画已知直线的平行线?相交与平行一、帖(线) 二、靠(尺)三、移(点)四、画(线)过已知直线外一点画它的平行线. 1注意观察!ab.P2如何画平行线?刚才的画法中,三角板起着什么作用?
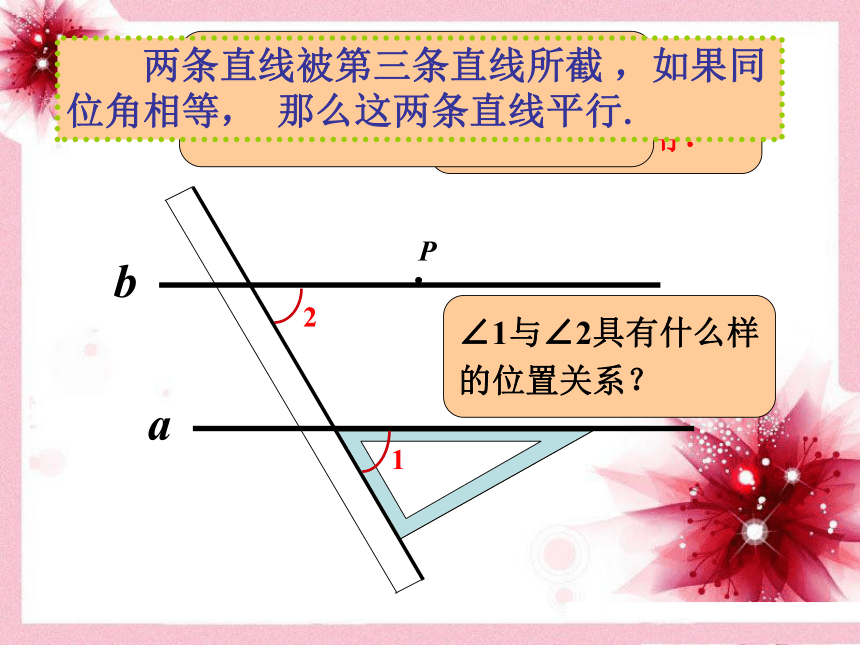
想一想!∠1与∠2具有什么样的位置关系? 我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行. 两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.平行线的判定方法1简单说成:同位角相等,两直线平行.何言
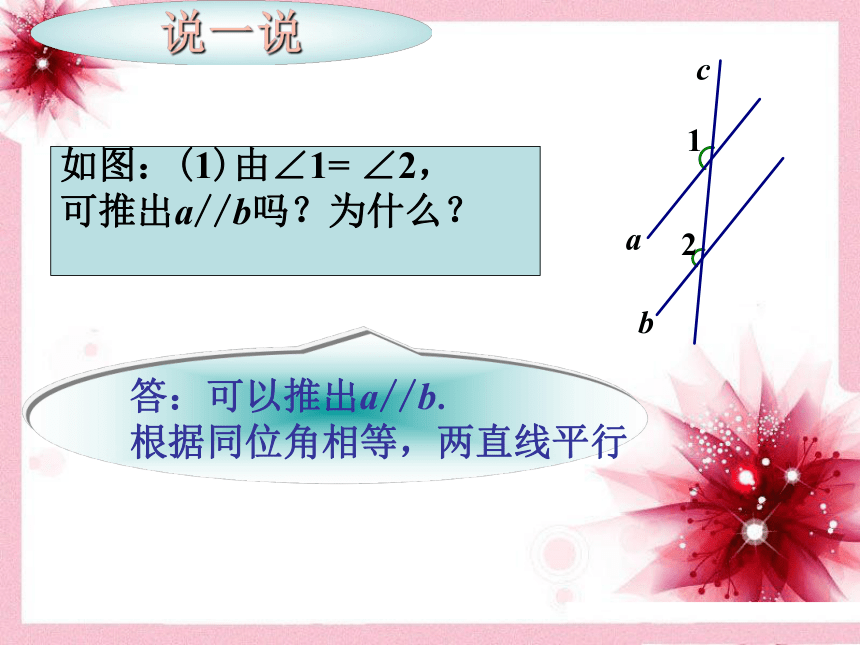
几语(同位角相等,两直线平行)∠1=∠2,AB∥CD.如图:(1)由∠1= ∠2,
可推出a//b吗?为什么?
说一说答:可以推出a//b.
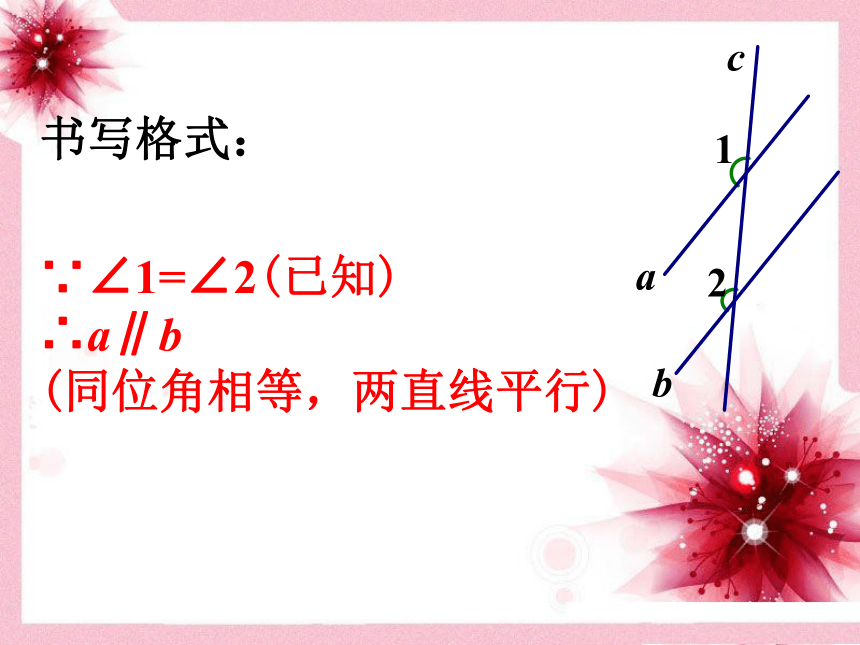
根据同位角相等,两直线平行∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)书写格式:例1 如图4-29,直线 AB,CD被直线EF所截, ∠1+∠2= 180o, AB与CD平行吗?为什么?图 4-29解 因为∠1+∠2=180o,
而∠1+∠3=180o,
所以∠2=∠3.
所以 AB∥CD
(同位角相等,两直线平行).例2 如图4-30,直线 a ,b 被直线c,d 所截, ∠1=∠2,说明为什么∠4=∠5.解 因为∠1=∠2 (已知)
∠2=∠3(对顶角相等)
所以∠1=∠3(等量代换)
所以a∥b(同位角相等, 两直线平行)
因此∠4=∠5(两直线平行,同位角相等) 1.如图,哪两个角相等能判定直线AB∥CD?DB1432AC 理解运用如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12∠1 =∠2(已知),
∠2 =∠3(对顶角相等),∠1 =∠3.AB∥CD(同位角相等,两直线平行). 两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.平行线的判定方法2简单说成:内错角相等,两直线平行.何言
几语(内错角相等,两直线平行)∠1=∠2,AB∥CD.如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?想一想练一练练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么? 如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF12∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),∠1 =∠3(同角的补角相等).探究23如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF132∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),∠1 =∠3(同角的补角相等).探究2 两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.平行线的判定方法3简单说成:同旁内角互补,两直线平行.何言
几语(同旁内角互补,两直线平行)∠1+∠2=180°,AB∥CD.如图:∠B=∠D=45°,∠C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ∠C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC想一想例3 如图 4-33,AB∥DC,∠BAD=∠BCD.
那么 AD∥BC 吗?图4-33解 因为AB∥DC,
所以∠1=∠2
(两直线平行,内错角相等).
又因为∠BAD=∠BCD,
所以∠BAD-∠1=∠BCD- ∠2.
即∠3=∠4.
所以 AD∥BC(内错角相等,两直线平行).例4 如图4-34,∠1=∠2= 50o , AD∥BC,
那么 AB∥DC 吗?图4-34解 因为AD∥BC,
所以∠1 + ∠3 = 180o
(两直线平行,同旁内角互补).
则∠3 = 180o -∠1
= 180o - 50o = 130o .
所以∠2 + ∠3 = 50o + 130o = 180o.
所以 AB∥DC(同旁内角互补,两直线平行).
判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc1234同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结
用所学方法来判断两条直线是否平行.
2、会根据判定方法进行简单的推理并学
会用数学符号写出简单的推理过程.
3、体会数学中的转化思想.重点:
1.了解平行线的定义,并能用符号表示.能借助三角板,方格纸等画平行线.
2.探索平行线的基本性质(基本事实).
难点:探索平行线的基本判定方法. 复习提问(1)平面内两条直线的位置关系有几种?(2)怎样过已知直线外一点画已知直线的平行线?相交与平行一、帖(线) 二、靠(尺)三、移(点)四、画(线)过已知直线外一点画它的平行线. 1注意观察!ab.P2如何画平行线?刚才的画法中,三角板起着什么作用?
想一想!∠1与∠2具有什么样的位置关系? 我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行. 两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.平行线的判定方法1简单说成:同位角相等,两直线平行.何言
几语(同位角相等,两直线平行)∠1=∠2,AB∥CD.如图:(1)由∠1= ∠2,
可推出a//b吗?为什么?
说一说答:可以推出a//b.
根据同位角相等,两直线平行∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)书写格式:例1 如图4-29,直线 AB,CD被直线EF所截, ∠1+∠2= 180o, AB与CD平行吗?为什么?图 4-29解 因为∠1+∠2=180o,
而∠1+∠3=180o,
所以∠2=∠3.
所以 AB∥CD
(同位角相等,两直线平行).例2 如图4-30,直线 a ,b 被直线c,d 所截, ∠1=∠2,说明为什么∠4=∠5.解 因为∠1=∠2 (已知)
∠2=∠3(对顶角相等)
所以∠1=∠3(等量代换)
所以a∥b(同位角相等, 两直线平行)
因此∠4=∠5(两直线平行,同位角相等) 1.如图,哪两个角相等能判定直线AB∥CD?DB1432AC 理解运用如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12∠1 =∠2(已知),
∠2 =∠3(对顶角相等),∠1 =∠3.AB∥CD(同位角相等,两直线平行). 两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.平行线的判定方法2简单说成:内错角相等,两直线平行.何言
几语(内错角相等,两直线平行)∠1=∠2,AB∥CD.如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?想一想练一练练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么? 如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF12∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),∠1 =∠3(同角的补角相等).探究23如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?ABCDEF132∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),∠1 =∠3(同角的补角相等).探究2 两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.平行线的判定方法3简单说成:同旁内角互补,两直线平行.何言
几语(同旁内角互补,两直线平行)∠1+∠2=180°,AB∥CD.如图:∠B=∠D=45°,∠C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ∠C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC想一想例3 如图 4-33,AB∥DC,∠BAD=∠BCD.
那么 AD∥BC 吗?图4-33解 因为AB∥DC,
所以∠1=∠2
(两直线平行,内错角相等).
又因为∠BAD=∠BCD,
所以∠BAD-∠1=∠BCD- ∠2.
即∠3=∠4.
所以 AD∥BC(内错角相等,两直线平行).例4 如图4-34,∠1=∠2= 50o , AD∥BC,
那么 AB∥DC 吗?图4-34解 因为AD∥BC,
所以∠1 + ∠3 = 180o
(两直线平行,同旁内角互补).
则∠3 = 180o -∠1
= 180o - 50o = 130o .
所以∠2 + ∠3 = 50o + 130o = 180o.
所以 AB∥DC(同旁内角互补,两直线平行).
判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc1234同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结
