沪科版七年级下第10章相交线、平行线与平移练习A卷
文档属性
| 名称 | 沪科版七年级下第10章相交线、平行线与平移练习A卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 473.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-09 00:00:00 | ||
图片预览




文档简介
沪科版七年级下第10章相交线、平行线与平移A卷
姓名:__________班级:__________考号:__________
一 、选择题(本大题共12小题)
1.下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
2.如图,OA⊥OB,若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.70°
3.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B. ∠3 C. ∠4 D. ∠5
4.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6 B.∠2=∠6 C.∠1=∠3 D.∠5=∠7
5.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为( )21世纪教育网版权所有
A.50° B.60° C.65° D.70°
6.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )21cnjy.com
A.4个 B. 3个 C. 2个 D. 1个
7.下列说法正确的是( )
A.同位角相等 B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角 D.在同一平面内,如果a∥b,b∥c,则a∥c
8.观察下面图案,在A.B、C、D四幅图案中,能通过如图的图案平移得到的是( )
A.B.C.D.
9.如图,直线a∥b,直线c与a、b相交,∠1=70°,则∠2的大小是( )
A.20° B.50° C.70° D.110°
10.将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2的度数为( )
A.30° B.45° C.50° D.60°
11.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )【来源:21·世纪·教育·网】
A.130° B.138° C.140° D.142°
12.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B. 35° C. 36° D. 40°
二 、填空题(本大题共8小题)
13.如图,已知a∥b,∠1=50°,则∠2= 度.
14.如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1= °.
15.一个角的度数为20°,则它的补角的度数为 .
16.如下图,∠1=∠2,∠A=60°,则∠ADC=_ _度.
17..如图,AB∥CD,AC⊥BC,∠ABC=35°,则∠1的度数为 .
18.如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,则∠D=__________,∠B=__________.
19.如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是 .
20.如图,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为 度(用关于α的代数式表示).www-2-1-cnjy-com
三 、解答题(本大题共8小题)
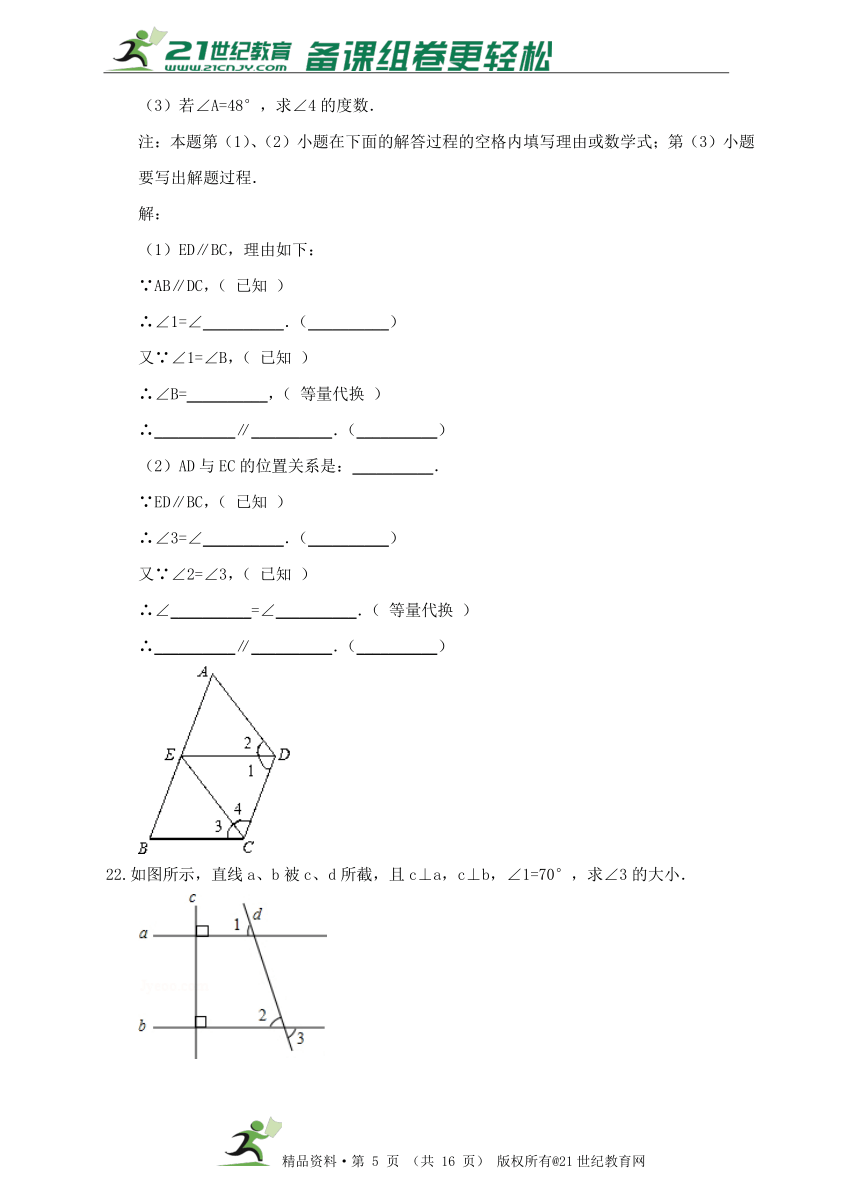
21.如图,AB∥DC,∠1=∠B,∠2=∠3.
(1)ED与BC平行吗?请说明理由;
(2)AD与EC的位置关系如何?为什么?
(3)若∠A=48°,求∠4的度数.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 )
∴∠1=∠__________.(__________)
又∵∠1=∠B,( 已知 )
∴∠B=__________,( 等量代换 )
∴__________∥__________.(__________)
(2)AD与EC的位置关系是:__________.
∵ED∥BC,( 已知 )
∴∠3=∠__________.(__________)
又∵∠2=∠3,( 已知 )
∴∠__________=∠__________.( 等量代换 )
∴__________∥__________.(__________)
22.如图所示,直线a、b被c、d所截,且c⊥a,c⊥b,∠1=70°,求∠3的大小.
23.读下列语句,并画出图形:
直线AB、CD是相交直线,点P是直线AB,CD外一点,直线EF经过点P,且与直线AB平行,与直线CD相交于点E.21*cnjy*com
24.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
25.已知:如图,AB∥EF,BC∥ED,AB,DE交于点G.
求证:∠B=∠E.
26.如图,在四边形ABCD中,∠A=104°﹣∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.21·世纪*教育网
27.如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
28.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
沪科版七年级下第10章相交线、平行线与平移A卷答案解析
一 、选择题
1.分析:根据对顶角的定义对各选项分析判断后利用排除法求解.
解:A.∠1与∠2不是对顶角,故A选项错误;
B、∠1与∠2是对顶角,故B选项正确;
C、∠1与∠2不是对顶角,故C选项错误;
D、∠1与∠2不是对顶角,故D选项错误.
故选:B.
2.分析: 根据两个角的和为 90°,可得两角互余,可得答案
解:∵OA⊥OB,
∴∠AOB=90°
又∵∠1=35°
∴∠2=∠AOB-∠1=90°-35°=55°,
故选C
3. 分析:根据同位角的定义解之
解:∠1的同位角是∠2,
故选:A.
4.分析:利用平行线的判定方法判断即可.
解:∵∠2=∠6(已知),
∴a∥b(同位角相等,两直线平行),
则能使a∥b的条件是∠2=∠6,
故选B
5.分析:根据平行线的性质和角平分线性质可求.
解:∵AB∥CD,
∴∠1+∠BEF=180°,∠2=∠BEG,
∴∠BEF=180°﹣50°=130°,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=65°,
∴∠2=65°.
故选C.
6. 分析:由互余的定义、平行线的性质,利用等量代换求解即可
解:∵斜边与这根直尺平行,
∴∠α=∠2,
又∵∠1+∠2=90°,
∴∠1+∠α=90°,
又∠α+∠3=90°
∴与α互余的角为∠1和∠3.
故选C.
7.. 分析:根据平行线的性质和判定以及对顶角的定义进行判断.
解:A.只有在两直线平行这一前提下,同位角才相等,故A选项错误;
B、在同一平面内,如果a⊥b,b⊥c,则a∥c,故B选项错误;
C、相等的角不一定是对顶角,因为对顶角还有位置限制,故C选项错误;
D、由平行公理的推论知,故D选项正确.
故选:D.
8.分析:根据平移的定义:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移可直接得到答案.www.21-cn-jy.com
解答: 解:根据平移得到的是B.
故选:B.
9.分析:首先根据对顶角相等可得∠1=∠3,进而得到∠3=70°,然后根据两直线平行,同位角相等可得∠2=∠3=70°.21教育名师原创作品
解:∵∠1=70°,
∴∠3=70°,
∵a∥b,
∴∠2=∠3=70°,
故选:C.
10.分析:根据平行线的性质得∠2=∠3,再根据互余得到∠3=60°,所以∠2=60°.
解:∵a∥b,
∴∠2=∠3,
∵∠1+∠3=90°,
∴∠3=90°﹣30°=60°,
∴∠2=60°.
故选:D.
11.分析:根据平行线的判定推出AB∥CD,根据平行线的性质求出∠BPF,即可求出∠2的度数.
解:如图:
∵AB⊥GH,CD⊥GH,
∴∠GMB=∠GOD=90°,
∴AB∥CD,
∴∠BPF=∠1=42°,
∴∠2=180°﹣∠BPF=180°﹣42°=138°,
故选B.
12. 分析:过点A作l1的平行线,过点B作l2的平行线,根据两直线平行,内错角相等可得∠3=∠1,∠4=∠2,再根据两直线平行,同旁内角互补求出∠CAB+∠ABD=180°,然后计算即可得解【来源:21cnj*y.co*m】
解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选A.
二 、填空题
13. 分析:本题直接利用两直线平行,同旁内角互补即可解题.
解:∵a∥b,∠1=50°,
∴∠2=180°﹣∠1=180°﹣50°=130°.
14.分析:先根据两直线平行的性质得到∠3=∠2,再根据平角的定义列方程即可得解.
解:∵AB∥CD,
∴∠3=∠2,
∵∠1=2∠2,
∴∠1=2∠3,
∴3∠3+60°=180°,
∴∠3=40°,
∴∠1=80°,
故答案为:80.
15. 分析:根据邻补角的定义列式求解
解:∵两角互补,和为180°,
∴它的补角=180°-20°=160°
故答案为160°
16.分析:先利用平行线的判定判定AB∥CD,再利用平行线的性质得出结论
解:∵∠1=∠2,
∴AB∥CD.
∴∠A+∠ADC=180°
.∵∠A=60°,
∴∠ADC=120°
17.分析: 首先根据平行线的性质可得∠ABC=∠BCD=35°,再根据垂线的定义可得∠ACB=90°,再利用平角的定义计算出∠1的度数.2-1-c-n-j-y
解答: 解:∵AB∥CD,
∴∠ABC=∠BCD=35°,
∵AC⊥BC,
∴∠ACB=90°,
∴∠1=180°﹣90°﹣35°=55°,
故答案为:55°.
18. 分析:由平行线的性质可知∠D=∠1,根据∠C和∠D互余可求得∠C,最后根据平行线的性质可求得∠B.21*cnjy*com
解答: 解:∵AB∥DC,
∴∠D=∠1=39°.
∵∠C和∠D互余,
∴∠C+∠D=90°.
∴∠C=90°﹣39°=51°.
∵AB∥DC,
∴∠B+∠C=180°.
∴∠B=180°﹣51°=129°.
故答案为:39°;129°.
19.分析:先根据直线a∥b,∠2=65°得出∠FDE的度数,再由EF⊥CD于点F可知∠DFE=90°,故可得出∠1的度数.21教育网
解:∵直线a∥b,∠2=65°,
∴∠FDE=∠2=65°,
∵EF⊥CD于点F,
∴∠DFE=90°,
∴∠1=90°﹣∠FDE=90°﹣65°=25°.
故答案为:25°.
20. 分析:根据∠ECA=α,∠ECA+∠ECB=180°可得:∠ECB=180°-α,根据CD平分∠ECB可得∠DCB=∠ECB=90°-α,根据FG∥CD可得:∠GFB=∠DCB=90°-α.
三 、解答题
21. 分析:只需要根据两直线平行的判定方法及性质填写对应的空即可
解:(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 ),
∴∠1=∠AED( 两直线平行,内错角相等 ),
又∵∠1=∠B( 已知 ),
∴∠B=∠AED( 等量代换 ),
∴ED∥BC( 同位角相等,两直线平行 ),
故答案为:AED,两直线平行,内错角相等,∠AED,ED,BC;
(2)AD与EC的位置关系是:AD∥EC,
∵ED∥BC( 已知 ),
∴∠3=∠CED( 两直线平行,内错角相等 ),
又∵∠2=∠3( 已知 ),
∴∠2=∠CED( 等量代换 ),
∴AD∥EC( 内错角相等,两直线平行 ),
故答案为:AD∥EC,CED,两直线平行,内错角相等,2,CED,AD,EC,内错角相等,两直线平行.2·1·c·n·j·y
22. 分析:根据题意可知a∥b,根据两直线平行同位角相等可知∠1=∠2,再根据对顶角相等即可得出∠3.【出处:21教育名师】
解答: 解:∵c⊥a,c⊥b,
∴a∥b,
∵∠1=70°
∴∠1=∠2=70°,
∴∠2=∠3=70°.
23. 分析:首先画出两条相交直线,然后再在直线AB,CD外确定点P,然后点P作直线EF与直线AB平行即可.【版权所有:21教育】
解答: 解:如图所示:
.
24. 分析:根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
解:BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=∠ABC,∠3=∠4=∠ADC(角平分线的定义).
∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).
25. 分析:由AB∥EF,BC∥ED,根据平行线的性质,即可得∠E=∠AGD,∠B=∠AGD,继而证得结论.
解答: 证明:∵AB∥EF,
∴∠E=∠AGD,
∵BC∥ED,
∴∠B=∠AGD,
∴∠B=∠E.
26. 分析:根据同旁内角互补,两直线平行先求出AD∥BC,然后根据两直线平行,内错角相等求出∠1=∠DBC,再根据垂直于同一直线的两直线互相平行求出BD∥EF,然后根据两直线平行,同位角相等即可得解.
解:能辨认∠1=∠2.
理由如下:∵∠A=104°﹣∠2,∠ABC=76°+∠2,
∴∠A+∠ABC=104°﹣∠2+76°+∠2=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠DBC(两直线平行,内错角相等),
∵BD⊥DC,EF⊥DC,
∴BD∥EF(根据垂直于同一直线的两直线平行),
∴∠2=∠DBC(两直线平行,同位角相等),
∴∠1=∠2.
27.分析:根据对顶角的性质得到BD∥CE的条件,然后根据平行线的性质得到∠B=∠C,已知∠C=∠D,则得到满足AB∥EF的条件,再根据两直线平行,内错角相等得到∠A=∠F.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.
28.分析:(1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;
(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.21·cn·jy·com
解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
姓名:__________班级:__________考号:__________
一 、选择题(本大题共12小题)
1.下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
2.如图,OA⊥OB,若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.70°
3.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B. ∠3 C. ∠4 D. ∠5
4.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6 B.∠2=∠6 C.∠1=∠3 D.∠5=∠7
5.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为( )21世纪教育网版权所有
A.50° B.60° C.65° D.70°
6.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )21cnjy.com
A.4个 B. 3个 C. 2个 D. 1个
7.下列说法正确的是( )
A.同位角相等 B.在同一平面内,如果a⊥b,b⊥c,则a⊥c
C.相等的角是对顶角 D.在同一平面内,如果a∥b,b∥c,则a∥c
8.观察下面图案,在A.B、C、D四幅图案中,能通过如图的图案平移得到的是( )
A.B.C.D.
9.如图,直线a∥b,直线c与a、b相交,∠1=70°,则∠2的大小是( )
A.20° B.50° C.70° D.110°
10.将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2的度数为( )
A.30° B.45° C.50° D.60°
11.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )【来源:21·世纪·教育·网】
A.130° B.138° C.140° D.142°
12.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B. 35° C. 36° D. 40°
二 、填空题(本大题共8小题)
13.如图,已知a∥b,∠1=50°,则∠2= 度.
14.如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1= °.
15.一个角的度数为20°,则它的补角的度数为 .
16.如下图,∠1=∠2,∠A=60°,则∠ADC=_ _度.
17..如图,AB∥CD,AC⊥BC,∠ABC=35°,则∠1的度数为 .
18.如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,则∠D=__________,∠B=__________.
19.如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是 .
20.如图,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为 度(用关于α的代数式表示).www-2-1-cnjy-com
三 、解答题(本大题共8小题)
21.如图,AB∥DC,∠1=∠B,∠2=∠3.
(1)ED与BC平行吗?请说明理由;
(2)AD与EC的位置关系如何?为什么?
(3)若∠A=48°,求∠4的度数.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 )
∴∠1=∠__________.(__________)
又∵∠1=∠B,( 已知 )
∴∠B=__________,( 等量代换 )
∴__________∥__________.(__________)
(2)AD与EC的位置关系是:__________.
∵ED∥BC,( 已知 )
∴∠3=∠__________.(__________)
又∵∠2=∠3,( 已知 )
∴∠__________=∠__________.( 等量代换 )
∴__________∥__________.(__________)
22.如图所示,直线a、b被c、d所截,且c⊥a,c⊥b,∠1=70°,求∠3的大小.
23.读下列语句,并画出图形:
直线AB、CD是相交直线,点P是直线AB,CD外一点,直线EF经过点P,且与直线AB平行,与直线CD相交于点E.21*cnjy*com
24.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
25.已知:如图,AB∥EF,BC∥ED,AB,DE交于点G.
求证:∠B=∠E.
26.如图,在四边形ABCD中,∠A=104°﹣∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.21·世纪*教育网
27.如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
28.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
沪科版七年级下第10章相交线、平行线与平移A卷答案解析
一 、选择题
1.分析:根据对顶角的定义对各选项分析判断后利用排除法求解.
解:A.∠1与∠2不是对顶角,故A选项错误;
B、∠1与∠2是对顶角,故B选项正确;
C、∠1与∠2不是对顶角,故C选项错误;
D、∠1与∠2不是对顶角,故D选项错误.
故选:B.
2.分析: 根据两个角的和为 90°,可得两角互余,可得答案
解:∵OA⊥OB,
∴∠AOB=90°
又∵∠1=35°
∴∠2=∠AOB-∠1=90°-35°=55°,
故选C
3. 分析:根据同位角的定义解之
解:∠1的同位角是∠2,
故选:A.
4.分析:利用平行线的判定方法判断即可.
解:∵∠2=∠6(已知),
∴a∥b(同位角相等,两直线平行),
则能使a∥b的条件是∠2=∠6,
故选B
5.分析:根据平行线的性质和角平分线性质可求.
解:∵AB∥CD,
∴∠1+∠BEF=180°,∠2=∠BEG,
∴∠BEF=180°﹣50°=130°,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=65°,
∴∠2=65°.
故选C.
6. 分析:由互余的定义、平行线的性质,利用等量代换求解即可
解:∵斜边与这根直尺平行,
∴∠α=∠2,
又∵∠1+∠2=90°,
∴∠1+∠α=90°,
又∠α+∠3=90°
∴与α互余的角为∠1和∠3.
故选C.
7.. 分析:根据平行线的性质和判定以及对顶角的定义进行判断.
解:A.只有在两直线平行这一前提下,同位角才相等,故A选项错误;
B、在同一平面内,如果a⊥b,b⊥c,则a∥c,故B选项错误;
C、相等的角不一定是对顶角,因为对顶角还有位置限制,故C选项错误;
D、由平行公理的推论知,故D选项正确.
故选:D.
8.分析:根据平移的定义:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移可直接得到答案.www.21-cn-jy.com
解答: 解:根据平移得到的是B.
故选:B.
9.分析:首先根据对顶角相等可得∠1=∠3,进而得到∠3=70°,然后根据两直线平行,同位角相等可得∠2=∠3=70°.21教育名师原创作品
解:∵∠1=70°,
∴∠3=70°,
∵a∥b,
∴∠2=∠3=70°,
故选:C.
10.分析:根据平行线的性质得∠2=∠3,再根据互余得到∠3=60°,所以∠2=60°.
解:∵a∥b,
∴∠2=∠3,
∵∠1+∠3=90°,
∴∠3=90°﹣30°=60°,
∴∠2=60°.
故选:D.
11.分析:根据平行线的判定推出AB∥CD,根据平行线的性质求出∠BPF,即可求出∠2的度数.
解:如图:
∵AB⊥GH,CD⊥GH,
∴∠GMB=∠GOD=90°,
∴AB∥CD,
∴∠BPF=∠1=42°,
∴∠2=180°﹣∠BPF=180°﹣42°=138°,
故选B.
12. 分析:过点A作l1的平行线,过点B作l2的平行线,根据两直线平行,内错角相等可得∠3=∠1,∠4=∠2,再根据两直线平行,同旁内角互补求出∠CAB+∠ABD=180°,然后计算即可得解【来源:21cnj*y.co*m】
解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选A.
二 、填空题
13. 分析:本题直接利用两直线平行,同旁内角互补即可解题.
解:∵a∥b,∠1=50°,
∴∠2=180°﹣∠1=180°﹣50°=130°.
14.分析:先根据两直线平行的性质得到∠3=∠2,再根据平角的定义列方程即可得解.
解:∵AB∥CD,
∴∠3=∠2,
∵∠1=2∠2,
∴∠1=2∠3,
∴3∠3+60°=180°,
∴∠3=40°,
∴∠1=80°,
故答案为:80.
15. 分析:根据邻补角的定义列式求解
解:∵两角互补,和为180°,
∴它的补角=180°-20°=160°
故答案为160°
16.分析:先利用平行线的判定判定AB∥CD,再利用平行线的性质得出结论
解:∵∠1=∠2,
∴AB∥CD.
∴∠A+∠ADC=180°
.∵∠A=60°,
∴∠ADC=120°
17.分析: 首先根据平行线的性质可得∠ABC=∠BCD=35°,再根据垂线的定义可得∠ACB=90°,再利用平角的定义计算出∠1的度数.2-1-c-n-j-y
解答: 解:∵AB∥CD,
∴∠ABC=∠BCD=35°,
∵AC⊥BC,
∴∠ACB=90°,
∴∠1=180°﹣90°﹣35°=55°,
故答案为:55°.
18. 分析:由平行线的性质可知∠D=∠1,根据∠C和∠D互余可求得∠C,最后根据平行线的性质可求得∠B.21*cnjy*com
解答: 解:∵AB∥DC,
∴∠D=∠1=39°.
∵∠C和∠D互余,
∴∠C+∠D=90°.
∴∠C=90°﹣39°=51°.
∵AB∥DC,
∴∠B+∠C=180°.
∴∠B=180°﹣51°=129°.
故答案为:39°;129°.
19.分析:先根据直线a∥b,∠2=65°得出∠FDE的度数,再由EF⊥CD于点F可知∠DFE=90°,故可得出∠1的度数.21教育网
解:∵直线a∥b,∠2=65°,
∴∠FDE=∠2=65°,
∵EF⊥CD于点F,
∴∠DFE=90°,
∴∠1=90°﹣∠FDE=90°﹣65°=25°.
故答案为:25°.
20. 分析:根据∠ECA=α,∠ECA+∠ECB=180°可得:∠ECB=180°-α,根据CD平分∠ECB可得∠DCB=∠ECB=90°-α,根据FG∥CD可得:∠GFB=∠DCB=90°-α.
三 、解答题
21. 分析:只需要根据两直线平行的判定方法及性质填写对应的空即可
解:(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 ),
∴∠1=∠AED( 两直线平行,内错角相等 ),
又∵∠1=∠B( 已知 ),
∴∠B=∠AED( 等量代换 ),
∴ED∥BC( 同位角相等,两直线平行 ),
故答案为:AED,两直线平行,内错角相等,∠AED,ED,BC;
(2)AD与EC的位置关系是:AD∥EC,
∵ED∥BC( 已知 ),
∴∠3=∠CED( 两直线平行,内错角相等 ),
又∵∠2=∠3( 已知 ),
∴∠2=∠CED( 等量代换 ),
∴AD∥EC( 内错角相等,两直线平行 ),
故答案为:AD∥EC,CED,两直线平行,内错角相等,2,CED,AD,EC,内错角相等,两直线平行.2·1·c·n·j·y
22. 分析:根据题意可知a∥b,根据两直线平行同位角相等可知∠1=∠2,再根据对顶角相等即可得出∠3.【出处:21教育名师】
解答: 解:∵c⊥a,c⊥b,
∴a∥b,
∵∠1=70°
∴∠1=∠2=70°,
∴∠2=∠3=70°.
23. 分析:首先画出两条相交直线,然后再在直线AB,CD外确定点P,然后点P作直线EF与直线AB平行即可.【版权所有:21教育】
解答: 解:如图所示:
.
24. 分析:根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
解:BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=∠ABC,∠3=∠4=∠ADC(角平分线的定义).
∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).
25. 分析:由AB∥EF,BC∥ED,根据平行线的性质,即可得∠E=∠AGD,∠B=∠AGD,继而证得结论.
解答: 证明:∵AB∥EF,
∴∠E=∠AGD,
∵BC∥ED,
∴∠B=∠AGD,
∴∠B=∠E.
26. 分析:根据同旁内角互补,两直线平行先求出AD∥BC,然后根据两直线平行,内错角相等求出∠1=∠DBC,再根据垂直于同一直线的两直线互相平行求出BD∥EF,然后根据两直线平行,同位角相等即可得解.
解:能辨认∠1=∠2.
理由如下:∵∠A=104°﹣∠2,∠ABC=76°+∠2,
∴∠A+∠ABC=104°﹣∠2+76°+∠2=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠DBC(两直线平行,内错角相等),
∵BD⊥DC,EF⊥DC,
∴BD∥EF(根据垂直于同一直线的两直线平行),
∴∠2=∠DBC(两直线平行,同位角相等),
∴∠1=∠2.
27.分析:根据对顶角的性质得到BD∥CE的条件,然后根据平行线的性质得到∠B=∠C,已知∠C=∠D,则得到满足AB∥EF的条件,再根据两直线平行,内错角相等得到∠A=∠F.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.
28.分析:(1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;
(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.21·cn·jy·com
解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
