1.4二次函数与一元二次方程的联系 同步教案 (1)
文档属性
| 名称 | 1.4二次函数与一元二次方程的联系 同步教案 (1) |
|
|
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-10 00:00:00 | ||
图片预览

文档简介
1.4
二次函数与一元二次方程的联系
教案
本节课的主要目的在于建立二次函数与一元二次方程之间的联系,渗透数形结合的思想
探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
你发现方程
x2-3x+2=0
的解x1、x2与A、B的坐标有什么联系?
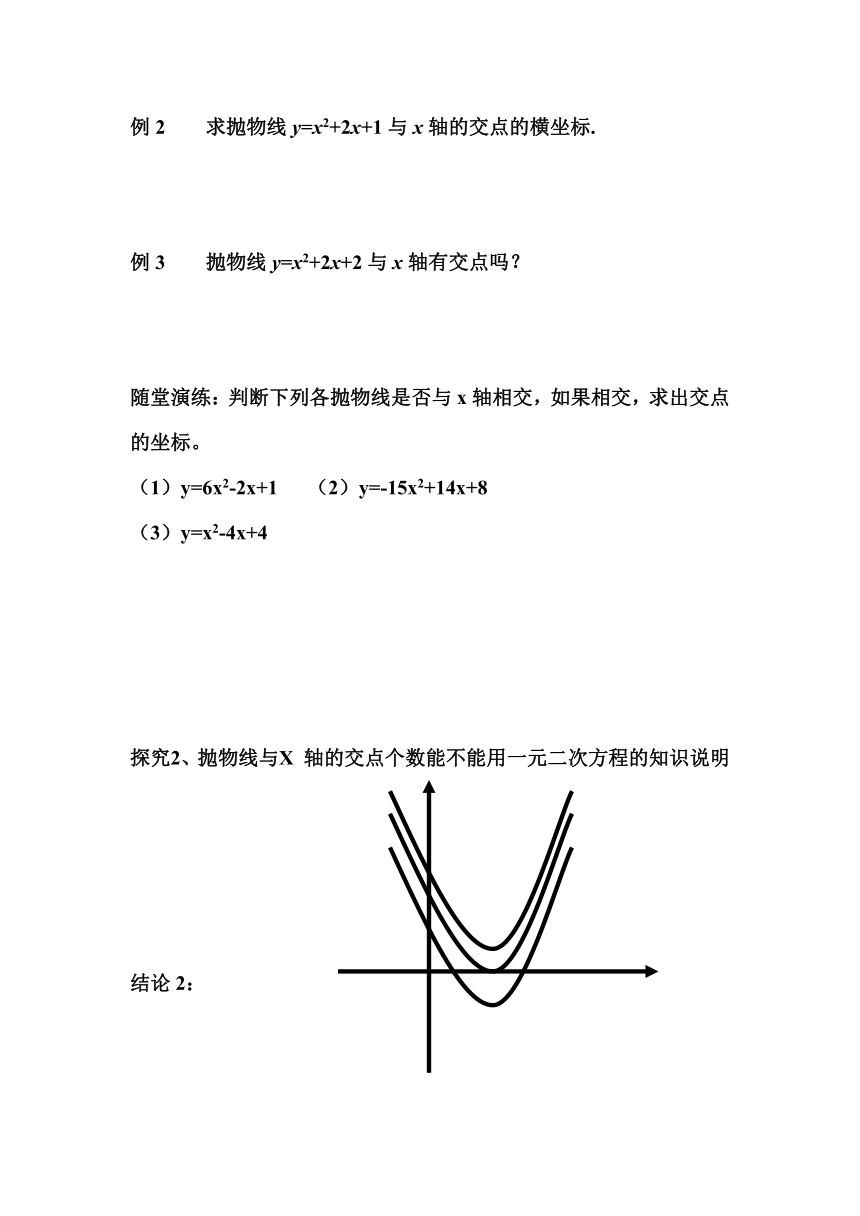
结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。
即:若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A(
),
B(
)
求抛物线y=4x2+12x+5与x轴的交点的横坐标.
求抛物线y=x2+2x+1与x轴的交点的横坐标.
抛物线y=x2+2x+2与x轴有交点吗?
随堂演练:判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4
探究2、抛物线与X
轴的交点个数能不能用一元二次方程的知识说明
结论2:
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
二次函数y=ax2+bx+c的图象与x轴交点
一元二次方程ax2+bx+c=0的根
b2-4ac
有两个交点
有一个交点
无交点
例1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)如果二次函数y=x2-kx-2+k与轴两个交点为A、B,设此抛物线与y轴的交点为C,当k为6时,求S△ABC
.
随堂演练:
1.若抛物线y=x -x+m与x轴没有公共点,则求m的取值范围。
2.求证:抛物线y=x +ax+a-2与x轴总有两个交点。
3.
已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,求m的值。
4
已知二次函数
的图像与X轴有两个不同的交点
(1)
求k的取值范围
(2)
当k为何值时,这两个交点横坐标的平方和等于50
课后作业
3
已知二次函数
(1)判别上述抛物线与X轴交点情况
(2)设抛物线与X轴交点之间距离为
,求k的值
O
A
B
x1
x2
y
x
二次函数与一元二次方程的联系
教案
本节课的主要目的在于建立二次函数与一元二次方程之间的联系,渗透数形结合的思想
探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
你发现方程
x2-3x+2=0
的解x1、x2与A、B的坐标有什么联系?
结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。
即:若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A(
),
B(
)
求抛物线y=4x2+12x+5与x轴的交点的横坐标.
求抛物线y=x2+2x+1与x轴的交点的横坐标.
抛物线y=x2+2x+2与x轴有交点吗?
随堂演练:判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4
探究2、抛物线与X
轴的交点个数能不能用一元二次方程的知识说明
结论2:
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
二次函数y=ax2+bx+c的图象与x轴交点
一元二次方程ax2+bx+c=0的根
b2-4ac
有两个交点
有一个交点
无交点
例1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)如果二次函数y=x2-kx-2+k与轴两个交点为A、B,设此抛物线与y轴的交点为C,当k为6时,求S△ABC
.
随堂演练:
1.若抛物线y=x -x+m与x轴没有公共点,则求m的取值范围。
2.求证:抛物线y=x +ax+a-2与x轴总有两个交点。
3.
已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,求m的值。
4
已知二次函数
的图像与X轴有两个不同的交点
(1)
求k的取值范围
(2)
当k为何值时,这两个交点横坐标的平方和等于50
课后作业
3
已知二次函数
(1)判别上述抛物线与X轴交点情况
(2)设抛物线与X轴交点之间距离为
,求k的值
O
A
B
x1
x2
y
x
