甘肃省天水三中2017届高三(上)第一次模拟数学试卷(文科)(解析版)
文档属性
| 名称 | 甘肃省天水三中2017届高三(上)第一次模拟数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 506.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-12 10:19:49 | ||
图片预览




文档简介
2016-2017学年甘肃省天水三中高三(上)第一次模拟数学试卷(文科)
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).
1.已知集合A={x|﹣1≤x≤1},B={x|x2﹣2x≤0},则A∩B=( )
A.[﹣1,0]
B.[﹣1,2]
C.[0,1]
D.(﹣∞,1]∪[2,+∞)
2.设复数z=1+i(i是虚数单位),则+z2=( )
A.1+i
B.1﹣i
C.﹣1﹣i
D.﹣1+i
3.已知||=1,||=,且⊥(﹣),则向量与向量的夹角为( )
A.
B.
C.
D.
4.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2﹣bc,bc=4,则△ABC的面积为( )
A.
B.1
C.
D.2
5.已知a∈{﹣2,0,1,3,4},b∈{1,2},则函数f(x)=(a2﹣2)x+b为增函数的概率是( )
A.
B.
C.
D.
6.阅读如图所示的程序框图,运行相应的程序,若输出的S为,则判断框中填写的内容可以是( )
A.n=6
B.n<6
C.n≤6
D.n≤8
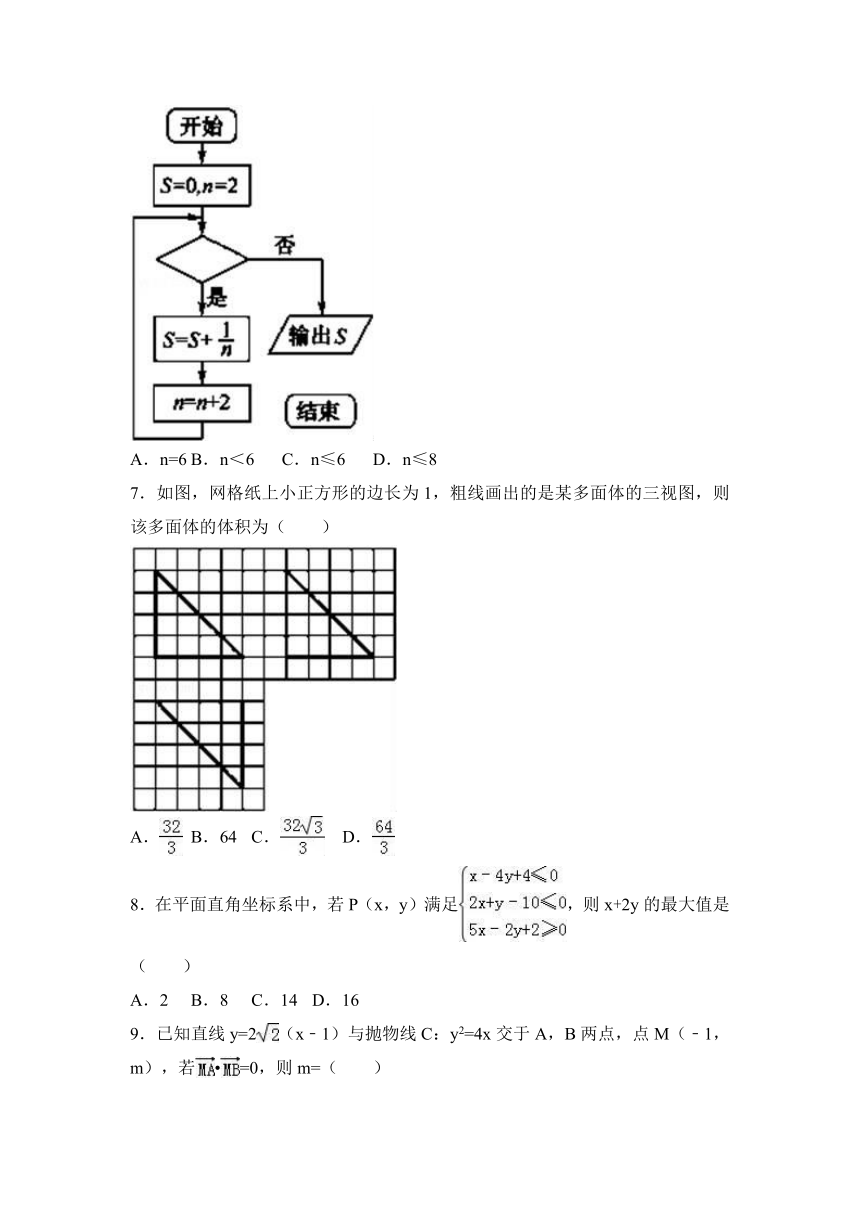
7.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )
A.
B.64
C.
D.
8.在平面直角坐标系中,若P(x,y)满足,则x+2y的最大值是( )
A.2
B.8
C.14
D.16
9.已知直线y=2(x﹣1)与抛物线C:y2=4x交于A,B两点,点M(﹣1,m),若 =0,则m=( )
A.
B.
C.
D.0
10.对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为M函数:
(i)
对任意的x∈[0,1],恒有f(x)≥0;
(ii)
当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.
则下列四个函数中不是M函数的个数是( )
①f(x)=x2②f(x)=x2+1
③f(x)=ln(x2+1)④f(x)=2x﹣1.
A.1
B.2
C.3
D.4
11.已知双曲线=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线左焦点F1(﹣1,0),则双曲线的离心率是( )
A.
B.
C.
D.
12.若对 x,y∈[0,+∞),不等式4ax≤ex+y﹣2+ex﹣y﹣2+2恒成立,则实数a的最大值是( )
A.
B.1
C.2
D.
二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上).
13.函数y=的单调递增区间是 .
14.(x﹣)6的展开式中常数项为 .
15.已知定义在R上的偶函数f(x)在[0,+∞)上单调递增,且f(1)=0,则不等式f(x﹣2)≥0的解集是 .
16.底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.已知同底的两个正三棱锥内接于同一个球.已知两个正三棱锥的底面边长为a,球的半径为R.设两个正三棱锥的侧面与底面所成的角分别为α、β,则tan(α+β)的值是 .
三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤).
17.已知数列{an}中,a1=1,其前n项的和为Sn,且满足an=(n≥2).
(1)求证:数列{}是等差数列;
(2)证明:当n≥2时,S1+S2+S3+…+Sn<.
18.如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
(Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.
19.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生
1号
2号
3号
4号
5号
甲班
6
5
7
9
8
乙班
4
8
9
7
7
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X和Y,试求X和Y的分布列和数学期望.
20.已知椭圆C:
+=1(a>b>0)的上顶点为(0,1),且离心率为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:过椭圆C1:
+=1(m>n>0)上一点Q(x0,y0)的切线方程为+=1;
(Ⅲ)过圆x2+y2=16上一点P向椭圆C引两条切线,切点分别为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求|MN|的最小值.
21.定义在R上的函数f(x)满足,.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较和ex﹣1+a哪个更靠近lnx,并说明理由.
[选修4-1:几何证明选讲]
22.如图所示,AB为圆O的直径,CB,CD为圆O的切线,B,D为切点.
(1)求证:AD∥OC;
(2)若圆O的半径为2,求AD OC的值.
[选修4-4:坐标系与参数方程]
23.在直角坐标系xOy中,圆C的参数方程为(θ为参数).
(1)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(2)已知A(﹣2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.
[选修4-5:不等式选讲]
24.(1)已知a,b都是正数,且a≠b,求证:a3+b3>a2b+ab2;
(2)已知a,b,c都是正数,求证:≥abc.
2016-2017学年甘肃省天水三中高三(上)第一次模拟数学试卷(文科)
参考答案与试题解析
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).
1.已知集合A={x|﹣1≤x≤1},B={x|x2﹣2x≤0},则A∩B=( )
A.[﹣1,0]
B.[﹣1,2]
C.[0,1]
D.(﹣∞,1]∪[2,+∞)
【考点】交集及其运算.
【分析】直接由一元二次不等式化简集合B,则A交B的答案可求.
【解答】解:∵B={x|x2﹣2x≤0}={x|0≤x≤2},
∴A∩B={x|﹣1≤x≤1}∩{x|0≤x≤2}={x|0≤x≤1}.
则A∩B的区间为:[0,1].
故选C.
2.设复数z=1+i(i是虚数单位),则+z2=( )
A.1+i
B.1﹣i
C.﹣1﹣i
D.﹣1+i
【考点】复数代数形式的乘除运算.
【分析】利用复数的运算法则、共轭复数的定义即可得出.
【解答】解:∵复数z=1+i,∴z2=2i,
则+z2===1﹣i+2i=1+i,
故选:A.
3.已知||=1,||=,且⊥(﹣),则向量与向量的夹角为( )
A.
B.
C.
D.
【考点】平面向量数量积的运算.
【分析】根据已知条件即可得到,所以,从而求得cos=,根据向量夹角的范围即可得出向量的夹角.
【解答】解:∵;
;
∴;
∴;
∴向量与的夹角为.
故选B.
4.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2﹣bc,bc=4,则△ABC的面积为( )
A.
B.1
C.
D.2
【考点】余弦定理.
【分析】由已知及余弦定理可求cosA,从而可求sinA的值,结合已知由三角形面积公式即可得解.
【解答】解:∵a2=b2+c2﹣bc,
∴由余弦定理可得:cosA===,又0<A<π,
∴可得A=60°,sinA=,
∵bc=4,
∴S△ABC=bcsinA==.
故选:C.
5.已知a∈{﹣2,0,1,3,4},b∈{1,2},则函数f(x)=(a2﹣2)x+b为增函数的概率是( )
A.
B.
C.
D.
【考点】几何概型.
【分析】首先求出所以事件个数就是集合元素个数5,然后求出满足使函数为增函数的元素个数为3,利用公式可得.
【解答】解:从集合{﹣2,0,1,3,4}中任选一个数有5种选法,使函数f(x)=(a2﹣2)x+b为增函数的是a2﹣2>0解得a>或者a<,所以满足此条件的a有﹣2,3,4共有3个,由古典概型公式得函数f(x)=(a2﹣2)x+b为增函数的概率是;
故选:B.
6.阅读如图所示的程序框图,运行相应的程序,若输出的S为,则判断框中填写的内容可以是( )
A.n=6
B.n<6
C.n≤6
D.n≤8
【考点】程序框图.
【分析】模拟执行程序框图,依次写出每次循环得到的S,n的值,当n=8时,S=,由题意,此时应该不满足条件,退出循环,输出S的值为,故判断框中填写的内容可以是n≤6.
【解答】解:模拟执行程序框图,可得
S=0,n=2
满足条件,S=,n=4
满足条件,S==,n=6
满足条件,S==,n=8
由题意,此时应该不满足条件,退出循环,输出S的值为,
故判断框中填写的内容可以是n≤6,
故选:C.
7.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )
A.
B.64
C.
D.
【考点】由三视图求面积、体积.
【分析】由三视图可知,该几何体是四个面都是直角三角形的三棱锥,利用条件所给数据,代入棱锥体积公式,可得答案.
【解答】解:由三视图,该几何体是四个面都是直角三角形的三棱锥,V==.
故选A.
8.在平面直角坐标系中,若P(x,y)满足,则x+2y的最大值是( )
A.2
B.8
C.14
D.16
【考点】简单线性规划.
【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
【解答】解:作出不等式对应的平面区域,
由z=x+2y,得y=﹣,
平移直线y=﹣,由图象可知当直线y=﹣经过点A时,
直线y=﹣的截距最大,此时z最大.
由,得,
即A(2,6),
此时z的最大值为z=2+2×6=14.
故选:C.
9.已知直线y=2(x﹣1)与抛物线C:y2=4x交于A,B两点,点M(﹣1,m),若 =0,则m=( )
A.
B.
C.
D.0
【考点】直线与圆锥曲线的关系.
【分析】直接利用直线方程与抛物线方程联立方程组求出AB坐标,通过数量积求解m即可.
【解答】解:由题意可得:,8x2﹣20x+8=0,解得x=2或x=,
则A(2,2)、B(,).
点M(﹣1,m),若 =0,
可得(3,2m)(,﹣)=0.
化简2m2﹣2m+1=0,解得m=.
故选:B.
10.对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为M函数:
(i)
对任意的x∈[0,1],恒有f(x)≥0;
(ii)
当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.
则下列四个函数中不是M函数的个数是( )
①f(x)=x2②f(x)=x2+1
③f(x)=ln(x2+1)④f(x)=2x﹣1.
A.1
B.2
C.3
D.4
【考点】函数与方程的综合运用.
【分析】利用已知条件函数的新定义,对四个选项逐一验证两个条件,判断即可.
【解答】解:(i)在[0,1]上,四个函数都满足;(ii)x1≥0,x2≥0,x1+x2≤1;
对于①,,∴①满足;
对于②,
=2x1x2﹣1<0,∴②不满足.
对于③,
=而x1≥0,x2≥0,∴,∴,∴,
∴,∴,∴③满足;
对于④,
=,∴④满足;
故选:A.
11.已知双曲线=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线左焦点F1(﹣1,0),则双曲线的离心率是( )
A.
B.
C.
D.
【考点】利用导数研究曲线上某点切线方程;双曲线的简单性质.
【分析】设出切点坐标,通过导数求出切线方程的斜率,利用斜率相等列出方程,即可求出切点坐标,然后求解双曲线的离心率.
【解答】解:设,函数y=的导数为:y′=,∴切线的斜率为,
又∵在点P处的切线过双曲线左焦点F(﹣1,0),∴,解得x0=1,
∴P(1,1),
双曲线的左焦点F1(﹣1,0),则双曲线的右焦点F2(1,0),既c=1.
则|PF1|﹣|PF2|=2a,既﹣=2a
解得a=
所以离心率e===
12.若对 x,y∈[0,+∞),不等式4ax≤ex+y﹣2+ex﹣y﹣2+2恒成立,则实数a的最大值是( )
A.
B.1
C.2
D.
【考点】函数恒成立问题.
【分析】利用基本不等式和参数分离可得a≤在x>0时恒成立,构造函数g(x)=,通过求导判断单调性求得g(x)的最小值即可得到a的最大值.
【解答】解:当x=0时,不等式即为0≤ey﹣2+e﹣y﹣2+2,显然成立;
当x>0时,设f(x)=ex+y﹣2+ex﹣y﹣2+2,
不等式4ax≤ex+y﹣2+ex﹣y﹣2+2恒成立,
即为不等式4ax≤f(x)恒成立.
即有f(x)=ex﹣2(ey+e﹣y)+2≥ex﹣2 2+2=2+2ex﹣2(当且仅当y=0时,取等号),
由题意可得4ax≤2+2ex﹣2,
即有a≤在x>0时恒成立,
令g(x)=,g′(x)=,
令g′(x)=0,即有(x﹣1)ex﹣2=1,
令h(x)=(x﹣1)ex﹣2,h′(x)=xex﹣2,
当x>0时h(x)递增,
由于h(2)=1,即有(x﹣1)ex﹣2=1的根为2,
当x>2时,g(x)递增,0<x<2时,g(x)递减,
即有x=2时,g(x)取得最小值,为,
则有a≤.
当x=2,y=0时,a取得最大值.
故选:D
二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上).
13.函数y=的单调递增区间是 [0,] .
【考点】两角和与差的余弦函数;正弦函数的图象.
【分析】化简可得y=sin(x+),解不等式2kπ﹣≤x+≤2kπ+可得函数所有的单调递增区间,结合x∈[0,]可得.
【解答】解:化简可得y=sinxcos+cosxsin=sin(x+),
由2kπ﹣≤x+≤2kπ+可得2kπ﹣≤x≤2kπ+,k∈Z,
当k=0时,可得函数的一个单调递增区间为[﹣,],
由x∈[0,]可得x∈[0,],
故答案为:[0,].
14.(x﹣)6的展开式中常数项为 ﹣ .
【考点】二项式系数的性质.
【分析】利用二项展开式的通项公式求出二项展开式的第r+1项,令x的指数为0得常数项.
【解答】解:展开式的通项公式为Tr+1=(﹣)rC6rx6﹣2r,
令6﹣2r=0得r=3,
得常数项为C63(﹣)3=﹣.
故答案为:﹣.
15.已知定义在R上的偶函数f(x)在[0,+∞)上单调递增,且f(1)=0,则不等式f(x﹣2)≥0的解集是 {x|x≥3或x≤1} .
【考点】抽象函数及其应用.
【分析】根据题意,分析可得不等式f(x﹣2)≥0等价为f(|x﹣2|)≥f(1),进而可以将其转化为|x﹣2|≥1,解可得答案.
【解答】解:∵偶函数f(x)在[0,+∞)上为增函数,f(1)=0,
∴不等式f(x﹣2)≥0等价为f(|x﹣2|)≥f(1),
即|x﹣2|≥1,
即x﹣2≥1或x﹣2≤﹣1,
即x≥3或x≤1,
故不等式的解集为{x|x≥3或x≤1},
故答案为:{x|x≥3或x≤1}.
16.底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.已知同底的两个正三棱锥内接于同一个球.已知两个正三棱锥的底面边长为a,球的半径为R.设两个正三棱锥的侧面与底面所成的角分别为α、β,则tan(α+β)的值是 .
【考点】两角和与差的正切函数;球内接多面体.
【分析】由题意画出图象以及过球心的截面圆,由球和正三棱锥的几何特征可得:两个正三棱锥的侧面与底面所成的角分别为α、β,再求出涉及的线段的长度,根据两角和的正切函数和正切函数的定义求出tan(α+β)的值.
【解答】解:由题意画出图象如下图:
由图得,右侧为该球过SA和球心的截面,由于三角形ABC为正三角形,
所以D为BC中点,且AD⊥BC,SD⊥BC,MD⊥BC,
故∠SDA=α,∠MDA=β.
设SM∩平面ABC=P,则点P为三角形ABC的重心,且点P在AD上,SM=2R,AB=a,
∴,
因此
=,
故答案为:.
三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤).
17.已知数列{an}中,a1=1,其前n项的和为Sn,且满足an=(n≥2).
(1)求证:数列{}是等差数列;
(2)证明:当n≥2时,S1+S2+S3+…+Sn<.
【考点】数列递推式;数列的求和.
【分析】(1)当n≥2时,Sn﹣Sn﹣1= Sn﹣Sn﹣1=2Sn Sn﹣1(n≥2),取倒数,可得﹣=2,利用等差数列的定义即可证得:数列{}是等差数列;
(2)由(1)可知,
=+(n﹣1)×2=2n﹣1 Sn=.n≥2时,
<= =(﹣),从而可证当n≥2时,S1+S2+S3+…+Sn<.
【解答】(本题满分12分)
证明:(1)当n≥2时,Sn﹣Sn﹣1=,
整理得:Sn﹣Sn﹣1=2Sn Sn﹣1(n≥2),
﹣=2,从而{}构成以1为首项,2为公差的等差数列.﹣﹣﹣﹣﹣﹣﹣
(2)由(1)可知,
=+(n﹣1)×2=2n﹣1,
∴Sn=.
∴当n≥2时,
<= =(﹣),
∴S1+S2+S3+…+Sn<1+(1﹣+﹣+…+﹣)<﹣<.
18.如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
(Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.
【考点】直线与平面所成的角;直线与平面平行的判定.
【分析】(Ⅰ)首先利用中点引出中位线,进一步得到线线平行,再利用线面平行的判定定理得到结论.
(Ⅱ)根据直线间的两两垂直,尽力空间直角坐标系,再求出平面PAB的法向量,最后利用向量的数量积求出线面的夹角的正弦值.
【解答】解:(Ⅰ)证明:作FM∥CD交PC于M.
∵点F为PD中点,
∴.
∵点E为AB的中点.
∴,
又AE∥FM,
∴四边形AEMF为平行四边形,
∴AF∥EM,
∵AF 平面PEC,EM 平面PEC,
∴直线AF∥平面PEC.
(Ⅱ)已知∠DAB=60°,
进一步求得:DE⊥DC,
则:建立空间直角坐标系,
则
P(0,0,1),C(0,1,0),E(,0,0),
A(,﹣,0),B(,,0).
所以:,.
设平面PAB的一个法向量为:,.
∵,
则:,
解得:,
所以平面PAB的法向量为:
∵,
∴设向量和的夹角为θ,
∴cosθ=,
∴PC平面PAB所成角的正弦值为.
19.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生
1号
2号
3号
4号
5号
甲班
6
5
7
9
8
乙班
4
8
9
7
7
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X和Y,试求X和Y的分布列和数学期望.
【考点】离散型随机变量及其分布列;极差、方差与标准差;离散型随机变量的期望与方差.
【分析】(1)求出两个班数据的平均值都为7,求出甲班的方差,乙班的方差,推出结果即可.
(2)X、Y可能取0,1,2,求出概率,得到分布列,然后分别求解期望.
【解答】解:(1)两个班数据的平均值都为7,
甲班的方差,
乙班的方差,
因为,甲班的方差较小,所以甲班的成绩比较稳定.
(2)X可能取0,1,2,,,,
所以X分布列为:
X
0
1
2
P
数学期望
Y可能取0,1,2,,,,
所以Y分布列为:
Y
0
1
2
P
数学期望.
20.已知椭圆C:
+=1(a>b>0)的上顶点为(0,1),且离心率为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:过椭圆C1:
+=1(m>n>0)上一点Q(x0,y0)的切线方程为+=1;
(Ⅲ)过圆x2+y2=16上一点P向椭圆C引两条切线,切点分别为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求|MN|的最小值.
【考点】直线与圆锥曲线的综合问题;椭圆的简单性质.
【分析】(Ⅰ)运用离心率公式和椭圆的a,b,c的关系,解得a,b,进而得到椭圆方程;
(Ⅱ)讨论直线的斜率不存在和存在,设出直线方程,联立椭圆方程,运用判别式为0,解得方程的一个跟,得到切点坐标和切线的斜率,进而得到切线方程;
(Ⅲ)设点P(xP,yP)为圆x2+y2=16上一点,求得切线PA,PB的方程,进而得到切点弦方程,再由两点的距离公式可得|MN|,结合基本不等式,即可得到最小值.
【解答】解:(Ⅰ)由题意可得b=1,e==,
又a2﹣b2=c2,解得a=2,b=1,
即有椭圆C方程为+y2=1.
(Ⅱ)证明:当斜率存在时,设切线方程为y=kx+t,联立椭圆方程+=1,
可得n2x2+m2(kx+t)2=m2n2,化简可得:
(n2+m2k2)x2+2m2ktx+m2(t2﹣n2)=0,①
由题可得:△=4m4k2t2﹣4m2(n2+m2k2)(t2﹣n2)=0
化简可得:t2=m2k2+n2,①式只有一个根,记作x0,
x0=﹣=﹣,x0为切点的横坐标,
切点的纵坐标y0=kx0+t=,
所以=﹣,所以k=﹣,
所以切线方程为:y﹣y0=k(x﹣x0)
=﹣(x﹣x0),
化简得:
+=1.
当切线斜率不存在时,切线为x=±m,也符合方程+=1,
综上+=1(m>n>0)上一点Q(x0,y0)的切线方程为+=1;
(Ⅲ)设点P(xP,yP)为圆x2+y2=16上一点,
PA,PB是椭圆+y2=1的切线,
切点A(x1,y1),B(x2,y2),过点A的椭圆的切线为+y1y=1,
过点B的椭圆的切线为+y2y=1.
由两切线都过P点,
+y1yP=1,
+y2yP=1
即有切点弦AB所在直线方程为+yyP=1.
M(0,),N(,0),
|MN|2=+=(+)
=(17++)≥(17+2)=,
当且仅当=即xP2=,yP2=时取等,
则|MN|,即|MN|的最小值为.
21.定义在R上的函数f(x)满足,.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较和ex﹣1+a哪个更靠近lnx,并说明理由.
【考点】导数在最大值、最小值问题中的应用;函数解析式的求解及常用方法;利用导数研究函数的单调性.
【分析】(1)求出函数的导数,利用赋值法,求出f′(1)=f′(1)+2﹣2f(0),得到f(0)=1.然后求解f′(1),即可求出函数的解析式.
(2)求出函数的导数g′(x)=ex+a,结合a≥0,a<0,分求解函数的单调区间即可.
(3)构造,通过函数的导数,判断函数的单调性,结合当1≤x≤e时,当1≤x≤e时,推出|p(x)|<|q(x)|,说明比ex﹣1+a更靠近lnx.当x>e时,通过作差,构造新函数,利用二次求导,判断函数的单调性,证明比ex﹣1+a更靠近lnx.
【解答】解:(1)f′(x)=f′(1)e2x﹣2+2x﹣2f(0),所以f′(1)=f′(1)+2﹣2f(0),即f(0)=1.又,
所以f′(1)=2e2,所以f(x)=e2x+x2﹣2x.
(2)∵f(x)=e2x﹣2x+x2,
∴,
∴g′(x)=ex﹣a.
①当a≤0时,g′(x)>0,函数f(x)在R上单调递增;
②当a>0时,由g′(x)=ex﹣a=0得x=lna,
∴x∈(﹣∞,lna)时,g′(x)<0,g(x)单调递减;x∈(lna,+∞)时,g′(x)>0,g(x)单调递增.
综上,当a≤0时,函数g(x)的单调递增区间为(∞,∞);
当a>0时,函数g(x)的单调递增区间为(lna,+∞),单调递减区间为(﹣∞,lna).
(3)解:设,∵,∴p(x)在x∈[1,+∞)上为减函数,又p(e)=0,∴当1≤x≤e时,p(x)≥0,当x>e时,p(x)<0.∵,,∴q′(x)在x∈[1,+∞)上为增函数,又q′(1)=0,∴x∈[1,+∞)时,q'(x)≥0,∴q(x)在x∈[1,+∞)上为增函数,∴q(x)≥q(1)=a+1>0.
①当1≤x≤e时,,
设,则,∴m(x)在x∈[1,+∞)上为减函数,
∴m(x)≤m(1)=e﹣1﹣a,
∵a≥2,∴m(x)<0,∴|p(x)|<|q(x)|,∴比ex﹣1+a更靠近lnx.
②当x>e时,,
设n(x)=2lnx﹣ex﹣1﹣a,则,,∴n′(x)在x>e时为减函数,
∴,∴n(x)在x>e时为减函数,∴n(x)<n(e)=2﹣a﹣ee﹣1<0,
∴|p(x)|<|q(x)|,∴比ex﹣1+a更靠近lnx.
综上:在a≥2,x≥1时,比ex﹣1+a更靠近lnx.
[选修4-1:几何证明选讲]
22.如图所示,AB为圆O的直径,CB,CD为圆O的切线,B,D为切点.
(1)求证:AD∥OC;
(2)若圆O的半径为2,求AD OC的值.
【考点】相似三角形的性质.
【分析】(1)连接BD,OD,利用切线的性质,证明BD⊥OC,利用AB为直径,证明AD⊥DB,即可证明AD∥OC;
(2)证明Rt△BAD∽Rt△COB,可得,即可求AD OC的值
【解答】(1)证明:连接BD,OD,
∵CB,CD是圆O的两条切线,
∴BD⊥OC,
又AB为直径,∴AD⊥DB,
∴AD∥OC.
(2)解:∵AD∥OC,∴∠DAB=∠COB,
∴Rt△BAD∽Rt△COB,
∴,
∴AD OC=AB OB=8.
[选修4-4:坐标系与参数方程]
23.在直角坐标系xOy中,圆C的参数方程为(θ为参数).
(1)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(2)已知A(﹣2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.
【考点】简单曲线的极坐标方程;参数方程化成普通方程.
【分析】(1)圆C的参数方程为,通过三角函数的平方关系式消去参数θ,得到普通方程.通过x=ρcosθ,y=ρsinθ,得到圆C的极坐标方程.
(2)求出点M(x,y)到直线AB:x﹣y+2=0的距离,表示出△ABM的面积,通过两角和的正弦函数,结合绝对值的几何意义,求解△ABM面积的最大值.
【解答】解:(1)圆C的参数方程为(θ为参数)
所以普通方程为(x﹣3)2+(y+4)2=4.,
x=ρcosθ,y=ρsinθ,可得(ρcosθ﹣3)2+(ρsinθ+4)2=4,
化简可得圆C的极坐标方程:ρ2﹣6ρcosθ+8ρsinθ+21=0.
(2)点M(x,y)到直线AB:x﹣y+2=0的距离为
△ABM的面积
所以△ABM面积的最大值为
[选修4-5:不等式选讲]
24.(1)已知a,b都是正数,且a≠b,求证:a3+b3>a2b+ab2;
(2)已知a,b,c都是正数,求证:≥abc.
【考点】不等式的证明.
【分析】(1)由条件a≠b推出:a2﹣2ab+b2>0,通过变形,应用不等式的性质可证出结论;
(2)利用基本不等式,再相加,即可证明结论.
【解答】证明:(1)∵a≠b,∴a﹣b≠0,∴a2﹣2ab+b2>0,∴a2﹣ab+b2>ab.
而a,b均为正数,∴a+b>0,∴(a+b)(a2﹣ab+b2)>ab(a+b)
∴a3+b3>a2b+ab2
成立;
(2)∵a,b,c都是正数,
∴a2b2+b2c2≥2acb2,a2b2+c2a2≥2bca2,c2a2+b2c2≥2abc2,
三式相加可得2(a2b2+b2c2+c2a2)≥2abc(a+b+c),
∴a2b2+b2c2+c2a2)≥abc(a+b+c),
∴≥abc.
2017年2月11日
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).
1.已知集合A={x|﹣1≤x≤1},B={x|x2﹣2x≤0},则A∩B=( )
A.[﹣1,0]
B.[﹣1,2]
C.[0,1]
D.(﹣∞,1]∪[2,+∞)
2.设复数z=1+i(i是虚数单位),则+z2=( )
A.1+i
B.1﹣i
C.﹣1﹣i
D.﹣1+i
3.已知||=1,||=,且⊥(﹣),则向量与向量的夹角为( )
A.
B.
C.
D.
4.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2﹣bc,bc=4,则△ABC的面积为( )
A.
B.1
C.
D.2
5.已知a∈{﹣2,0,1,3,4},b∈{1,2},则函数f(x)=(a2﹣2)x+b为增函数的概率是( )
A.
B.
C.
D.
6.阅读如图所示的程序框图,运行相应的程序,若输出的S为,则判断框中填写的内容可以是( )
A.n=6
B.n<6
C.n≤6
D.n≤8
7.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )
A.
B.64
C.
D.
8.在平面直角坐标系中,若P(x,y)满足,则x+2y的最大值是( )
A.2
B.8
C.14
D.16
9.已知直线y=2(x﹣1)与抛物线C:y2=4x交于A,B两点,点M(﹣1,m),若 =0,则m=( )
A.
B.
C.
D.0
10.对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为M函数:
(i)
对任意的x∈[0,1],恒有f(x)≥0;
(ii)
当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.
则下列四个函数中不是M函数的个数是( )
①f(x)=x2②f(x)=x2+1
③f(x)=ln(x2+1)④f(x)=2x﹣1.
A.1
B.2
C.3
D.4
11.已知双曲线=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线左焦点F1(﹣1,0),则双曲线的离心率是( )
A.
B.
C.
D.
12.若对 x,y∈[0,+∞),不等式4ax≤ex+y﹣2+ex﹣y﹣2+2恒成立,则实数a的最大值是( )
A.
B.1
C.2
D.
二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上).
13.函数y=的单调递增区间是 .
14.(x﹣)6的展开式中常数项为 .
15.已知定义在R上的偶函数f(x)在[0,+∞)上单调递增,且f(1)=0,则不等式f(x﹣2)≥0的解集是 .
16.底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.已知同底的两个正三棱锥内接于同一个球.已知两个正三棱锥的底面边长为a,球的半径为R.设两个正三棱锥的侧面与底面所成的角分别为α、β,则tan(α+β)的值是 .
三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤).
17.已知数列{an}中,a1=1,其前n项的和为Sn,且满足an=(n≥2).
(1)求证:数列{}是等差数列;
(2)证明:当n≥2时,S1+S2+S3+…+Sn<.
18.如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
(Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.
19.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生
1号
2号
3号
4号
5号
甲班
6
5
7
9
8
乙班
4
8
9
7
7
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X和Y,试求X和Y的分布列和数学期望.
20.已知椭圆C:
+=1(a>b>0)的上顶点为(0,1),且离心率为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:过椭圆C1:
+=1(m>n>0)上一点Q(x0,y0)的切线方程为+=1;
(Ⅲ)过圆x2+y2=16上一点P向椭圆C引两条切线,切点分别为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求|MN|的最小值.
21.定义在R上的函数f(x)满足,.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较和ex﹣1+a哪个更靠近lnx,并说明理由.
[选修4-1:几何证明选讲]
22.如图所示,AB为圆O的直径,CB,CD为圆O的切线,B,D为切点.
(1)求证:AD∥OC;
(2)若圆O的半径为2,求AD OC的值.
[选修4-4:坐标系与参数方程]
23.在直角坐标系xOy中,圆C的参数方程为(θ为参数).
(1)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(2)已知A(﹣2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.
[选修4-5:不等式选讲]
24.(1)已知a,b都是正数,且a≠b,求证:a3+b3>a2b+ab2;
(2)已知a,b,c都是正数,求证:≥abc.
2016-2017学年甘肃省天水三中高三(上)第一次模拟数学试卷(文科)
参考答案与试题解析
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).
1.已知集合A={x|﹣1≤x≤1},B={x|x2﹣2x≤0},则A∩B=( )
A.[﹣1,0]
B.[﹣1,2]
C.[0,1]
D.(﹣∞,1]∪[2,+∞)
【考点】交集及其运算.
【分析】直接由一元二次不等式化简集合B,则A交B的答案可求.
【解答】解:∵B={x|x2﹣2x≤0}={x|0≤x≤2},
∴A∩B={x|﹣1≤x≤1}∩{x|0≤x≤2}={x|0≤x≤1}.
则A∩B的区间为:[0,1].
故选C.
2.设复数z=1+i(i是虚数单位),则+z2=( )
A.1+i
B.1﹣i
C.﹣1﹣i
D.﹣1+i
【考点】复数代数形式的乘除运算.
【分析】利用复数的运算法则、共轭复数的定义即可得出.
【解答】解:∵复数z=1+i,∴z2=2i,
则+z2===1﹣i+2i=1+i,
故选:A.
3.已知||=1,||=,且⊥(﹣),则向量与向量的夹角为( )
A.
B.
C.
D.
【考点】平面向量数量积的运算.
【分析】根据已知条件即可得到,所以,从而求得cos=,根据向量夹角的范围即可得出向量的夹角.
【解答】解:∵;
;
∴;
∴;
∴向量与的夹角为.
故选B.
4.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2﹣bc,bc=4,则△ABC的面积为( )
A.
B.1
C.
D.2
【考点】余弦定理.
【分析】由已知及余弦定理可求cosA,从而可求sinA的值,结合已知由三角形面积公式即可得解.
【解答】解:∵a2=b2+c2﹣bc,
∴由余弦定理可得:cosA===,又0<A<π,
∴可得A=60°,sinA=,
∵bc=4,
∴S△ABC=bcsinA==.
故选:C.
5.已知a∈{﹣2,0,1,3,4},b∈{1,2},则函数f(x)=(a2﹣2)x+b为增函数的概率是( )
A.
B.
C.
D.
【考点】几何概型.
【分析】首先求出所以事件个数就是集合元素个数5,然后求出满足使函数为增函数的元素个数为3,利用公式可得.
【解答】解:从集合{﹣2,0,1,3,4}中任选一个数有5种选法,使函数f(x)=(a2﹣2)x+b为增函数的是a2﹣2>0解得a>或者a<,所以满足此条件的a有﹣2,3,4共有3个,由古典概型公式得函数f(x)=(a2﹣2)x+b为增函数的概率是;
故选:B.
6.阅读如图所示的程序框图,运行相应的程序,若输出的S为,则判断框中填写的内容可以是( )
A.n=6
B.n<6
C.n≤6
D.n≤8
【考点】程序框图.
【分析】模拟执行程序框图,依次写出每次循环得到的S,n的值,当n=8时,S=,由题意,此时应该不满足条件,退出循环,输出S的值为,故判断框中填写的内容可以是n≤6.
【解答】解:模拟执行程序框图,可得
S=0,n=2
满足条件,S=,n=4
满足条件,S==,n=6
满足条件,S==,n=8
由题意,此时应该不满足条件,退出循环,输出S的值为,
故判断框中填写的内容可以是n≤6,
故选:C.
7.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )
A.
B.64
C.
D.
【考点】由三视图求面积、体积.
【分析】由三视图可知,该几何体是四个面都是直角三角形的三棱锥,利用条件所给数据,代入棱锥体积公式,可得答案.
【解答】解:由三视图,该几何体是四个面都是直角三角形的三棱锥,V==.
故选A.
8.在平面直角坐标系中,若P(x,y)满足,则x+2y的最大值是( )
A.2
B.8
C.14
D.16
【考点】简单线性规划.
【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
【解答】解:作出不等式对应的平面区域,
由z=x+2y,得y=﹣,
平移直线y=﹣,由图象可知当直线y=﹣经过点A时,
直线y=﹣的截距最大,此时z最大.
由,得,
即A(2,6),
此时z的最大值为z=2+2×6=14.
故选:C.
9.已知直线y=2(x﹣1)与抛物线C:y2=4x交于A,B两点,点M(﹣1,m),若 =0,则m=( )
A.
B.
C.
D.0
【考点】直线与圆锥曲线的关系.
【分析】直接利用直线方程与抛物线方程联立方程组求出AB坐标,通过数量积求解m即可.
【解答】解:由题意可得:,8x2﹣20x+8=0,解得x=2或x=,
则A(2,2)、B(,).
点M(﹣1,m),若 =0,
可得(3,2m)(,﹣)=0.
化简2m2﹣2m+1=0,解得m=.
故选:B.
10.对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为M函数:
(i)
对任意的x∈[0,1],恒有f(x)≥0;
(ii)
当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.
则下列四个函数中不是M函数的个数是( )
①f(x)=x2②f(x)=x2+1
③f(x)=ln(x2+1)④f(x)=2x﹣1.
A.1
B.2
C.3
D.4
【考点】函数与方程的综合运用.
【分析】利用已知条件函数的新定义,对四个选项逐一验证两个条件,判断即可.
【解答】解:(i)在[0,1]上,四个函数都满足;(ii)x1≥0,x2≥0,x1+x2≤1;
对于①,,∴①满足;
对于②,
=2x1x2﹣1<0,∴②不满足.
对于③,
=而x1≥0,x2≥0,∴,∴,∴,
∴,∴,∴③满足;
对于④,
=,∴④满足;
故选:A.
11.已知双曲线=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线左焦点F1(﹣1,0),则双曲线的离心率是( )
A.
B.
C.
D.
【考点】利用导数研究曲线上某点切线方程;双曲线的简单性质.
【分析】设出切点坐标,通过导数求出切线方程的斜率,利用斜率相等列出方程,即可求出切点坐标,然后求解双曲线的离心率.
【解答】解:设,函数y=的导数为:y′=,∴切线的斜率为,
又∵在点P处的切线过双曲线左焦点F(﹣1,0),∴,解得x0=1,
∴P(1,1),
双曲线的左焦点F1(﹣1,0),则双曲线的右焦点F2(1,0),既c=1.
则|PF1|﹣|PF2|=2a,既﹣=2a
解得a=
所以离心率e===
12.若对 x,y∈[0,+∞),不等式4ax≤ex+y﹣2+ex﹣y﹣2+2恒成立,则实数a的最大值是( )
A.
B.1
C.2
D.
【考点】函数恒成立问题.
【分析】利用基本不等式和参数分离可得a≤在x>0时恒成立,构造函数g(x)=,通过求导判断单调性求得g(x)的最小值即可得到a的最大值.
【解答】解:当x=0时,不等式即为0≤ey﹣2+e﹣y﹣2+2,显然成立;
当x>0时,设f(x)=ex+y﹣2+ex﹣y﹣2+2,
不等式4ax≤ex+y﹣2+ex﹣y﹣2+2恒成立,
即为不等式4ax≤f(x)恒成立.
即有f(x)=ex﹣2(ey+e﹣y)+2≥ex﹣2 2+2=2+2ex﹣2(当且仅当y=0时,取等号),
由题意可得4ax≤2+2ex﹣2,
即有a≤在x>0时恒成立,
令g(x)=,g′(x)=,
令g′(x)=0,即有(x﹣1)ex﹣2=1,
令h(x)=(x﹣1)ex﹣2,h′(x)=xex﹣2,
当x>0时h(x)递增,
由于h(2)=1,即有(x﹣1)ex﹣2=1的根为2,
当x>2时,g(x)递增,0<x<2时,g(x)递减,
即有x=2时,g(x)取得最小值,为,
则有a≤.
当x=2,y=0时,a取得最大值.
故选:D
二、填空题(本大题包括4小题,每小题5分,共20分,把正确答案填在答题卡中的横线上).
13.函数y=的单调递增区间是 [0,] .
【考点】两角和与差的余弦函数;正弦函数的图象.
【分析】化简可得y=sin(x+),解不等式2kπ﹣≤x+≤2kπ+可得函数所有的单调递增区间,结合x∈[0,]可得.
【解答】解:化简可得y=sinxcos+cosxsin=sin(x+),
由2kπ﹣≤x+≤2kπ+可得2kπ﹣≤x≤2kπ+,k∈Z,
当k=0时,可得函数的一个单调递增区间为[﹣,],
由x∈[0,]可得x∈[0,],
故答案为:[0,].
14.(x﹣)6的展开式中常数项为 ﹣ .
【考点】二项式系数的性质.
【分析】利用二项展开式的通项公式求出二项展开式的第r+1项,令x的指数为0得常数项.
【解答】解:展开式的通项公式为Tr+1=(﹣)rC6rx6﹣2r,
令6﹣2r=0得r=3,
得常数项为C63(﹣)3=﹣.
故答案为:﹣.
15.已知定义在R上的偶函数f(x)在[0,+∞)上单调递增,且f(1)=0,则不等式f(x﹣2)≥0的解集是 {x|x≥3或x≤1} .
【考点】抽象函数及其应用.
【分析】根据题意,分析可得不等式f(x﹣2)≥0等价为f(|x﹣2|)≥f(1),进而可以将其转化为|x﹣2|≥1,解可得答案.
【解答】解:∵偶函数f(x)在[0,+∞)上为增函数,f(1)=0,
∴不等式f(x﹣2)≥0等价为f(|x﹣2|)≥f(1),
即|x﹣2|≥1,
即x﹣2≥1或x﹣2≤﹣1,
即x≥3或x≤1,
故不等式的解集为{x|x≥3或x≤1},
故答案为:{x|x≥3或x≤1}.
16.底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.已知同底的两个正三棱锥内接于同一个球.已知两个正三棱锥的底面边长为a,球的半径为R.设两个正三棱锥的侧面与底面所成的角分别为α、β,则tan(α+β)的值是 .
【考点】两角和与差的正切函数;球内接多面体.
【分析】由题意画出图象以及过球心的截面圆,由球和正三棱锥的几何特征可得:两个正三棱锥的侧面与底面所成的角分别为α、β,再求出涉及的线段的长度,根据两角和的正切函数和正切函数的定义求出tan(α+β)的值.
【解答】解:由题意画出图象如下图:
由图得,右侧为该球过SA和球心的截面,由于三角形ABC为正三角形,
所以D为BC中点,且AD⊥BC,SD⊥BC,MD⊥BC,
故∠SDA=α,∠MDA=β.
设SM∩平面ABC=P,则点P为三角形ABC的重心,且点P在AD上,SM=2R,AB=a,
∴,
因此
=,
故答案为:.
三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤).
17.已知数列{an}中,a1=1,其前n项的和为Sn,且满足an=(n≥2).
(1)求证:数列{}是等差数列;
(2)证明:当n≥2时,S1+S2+S3+…+Sn<.
【考点】数列递推式;数列的求和.
【分析】(1)当n≥2时,Sn﹣Sn﹣1= Sn﹣Sn﹣1=2Sn Sn﹣1(n≥2),取倒数,可得﹣=2,利用等差数列的定义即可证得:数列{}是等差数列;
(2)由(1)可知,
=+(n﹣1)×2=2n﹣1 Sn=.n≥2时,
<= =(﹣),从而可证当n≥2时,S1+S2+S3+…+Sn<.
【解答】(本题满分12分)
证明:(1)当n≥2时,Sn﹣Sn﹣1=,
整理得:Sn﹣Sn﹣1=2Sn Sn﹣1(n≥2),
﹣=2,从而{}构成以1为首项,2为公差的等差数列.﹣﹣﹣﹣﹣﹣﹣
(2)由(1)可知,
=+(n﹣1)×2=2n﹣1,
∴Sn=.
∴当n≥2时,
<= =(﹣),
∴S1+S2+S3+…+Sn<1+(1﹣+﹣+…+﹣)<﹣<.
18.如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
(Ⅰ)求证:直线AF∥平面PEC;
(Ⅱ)求PC与平面PAB所成角的正弦值.
【考点】直线与平面所成的角;直线与平面平行的判定.
【分析】(Ⅰ)首先利用中点引出中位线,进一步得到线线平行,再利用线面平行的判定定理得到结论.
(Ⅱ)根据直线间的两两垂直,尽力空间直角坐标系,再求出平面PAB的法向量,最后利用向量的数量积求出线面的夹角的正弦值.
【解答】解:(Ⅰ)证明:作FM∥CD交PC于M.
∵点F为PD中点,
∴.
∵点E为AB的中点.
∴,
又AE∥FM,
∴四边形AEMF为平行四边形,
∴AF∥EM,
∵AF 平面PEC,EM 平面PEC,
∴直线AF∥平面PEC.
(Ⅱ)已知∠DAB=60°,
进一步求得:DE⊥DC,
则:建立空间直角坐标系,
则
P(0,0,1),C(0,1,0),E(,0,0),
A(,﹣,0),B(,,0).
所以:,.
设平面PAB的一个法向量为:,.
∵,
则:,
解得:,
所以平面PAB的法向量为:
∵,
∴设向量和的夹角为θ,
∴cosθ=,
∴PC平面PAB所成角的正弦值为.
19.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生
1号
2号
3号
4号
5号
甲班
6
5
7
9
8
乙班
4
8
9
7
7
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作X和Y,试求X和Y的分布列和数学期望.
【考点】离散型随机变量及其分布列;极差、方差与标准差;离散型随机变量的期望与方差.
【分析】(1)求出两个班数据的平均值都为7,求出甲班的方差,乙班的方差,推出结果即可.
(2)X、Y可能取0,1,2,求出概率,得到分布列,然后分别求解期望.
【解答】解:(1)两个班数据的平均值都为7,
甲班的方差,
乙班的方差,
因为,甲班的方差较小,所以甲班的成绩比较稳定.
(2)X可能取0,1,2,,,,
所以X分布列为:
X
0
1
2
P
数学期望
Y可能取0,1,2,,,,
所以Y分布列为:
Y
0
1
2
P
数学期望.
20.已知椭圆C:
+=1(a>b>0)的上顶点为(0,1),且离心率为.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:过椭圆C1:
+=1(m>n>0)上一点Q(x0,y0)的切线方程为+=1;
(Ⅲ)过圆x2+y2=16上一点P向椭圆C引两条切线,切点分别为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求|MN|的最小值.
【考点】直线与圆锥曲线的综合问题;椭圆的简单性质.
【分析】(Ⅰ)运用离心率公式和椭圆的a,b,c的关系,解得a,b,进而得到椭圆方程;
(Ⅱ)讨论直线的斜率不存在和存在,设出直线方程,联立椭圆方程,运用判别式为0,解得方程的一个跟,得到切点坐标和切线的斜率,进而得到切线方程;
(Ⅲ)设点P(xP,yP)为圆x2+y2=16上一点,求得切线PA,PB的方程,进而得到切点弦方程,再由两点的距离公式可得|MN|,结合基本不等式,即可得到最小值.
【解答】解:(Ⅰ)由题意可得b=1,e==,
又a2﹣b2=c2,解得a=2,b=1,
即有椭圆C方程为+y2=1.
(Ⅱ)证明:当斜率存在时,设切线方程为y=kx+t,联立椭圆方程+=1,
可得n2x2+m2(kx+t)2=m2n2,化简可得:
(n2+m2k2)x2+2m2ktx+m2(t2﹣n2)=0,①
由题可得:△=4m4k2t2﹣4m2(n2+m2k2)(t2﹣n2)=0
化简可得:t2=m2k2+n2,①式只有一个根,记作x0,
x0=﹣=﹣,x0为切点的横坐标,
切点的纵坐标y0=kx0+t=,
所以=﹣,所以k=﹣,
所以切线方程为:y﹣y0=k(x﹣x0)
=﹣(x﹣x0),
化简得:
+=1.
当切线斜率不存在时,切线为x=±m,也符合方程+=1,
综上+=1(m>n>0)上一点Q(x0,y0)的切线方程为+=1;
(Ⅲ)设点P(xP,yP)为圆x2+y2=16上一点,
PA,PB是椭圆+y2=1的切线,
切点A(x1,y1),B(x2,y2),过点A的椭圆的切线为+y1y=1,
过点B的椭圆的切线为+y2y=1.
由两切线都过P点,
+y1yP=1,
+y2yP=1
即有切点弦AB所在直线方程为+yyP=1.
M(0,),N(,0),
|MN|2=+=(+)
=(17++)≥(17+2)=,
当且仅当=即xP2=,yP2=时取等,
则|MN|,即|MN|的最小值为.
21.定义在R上的函数f(x)满足,.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较和ex﹣1+a哪个更靠近lnx,并说明理由.
【考点】导数在最大值、最小值问题中的应用;函数解析式的求解及常用方法;利用导数研究函数的单调性.
【分析】(1)求出函数的导数,利用赋值法,求出f′(1)=f′(1)+2﹣2f(0),得到f(0)=1.然后求解f′(1),即可求出函数的解析式.
(2)求出函数的导数g′(x)=ex+a,结合a≥0,a<0,分求解函数的单调区间即可.
(3)构造,通过函数的导数,判断函数的单调性,结合当1≤x≤e时,当1≤x≤e时,推出|p(x)|<|q(x)|,说明比ex﹣1+a更靠近lnx.当x>e时,通过作差,构造新函数,利用二次求导,判断函数的单调性,证明比ex﹣1+a更靠近lnx.
【解答】解:(1)f′(x)=f′(1)e2x﹣2+2x﹣2f(0),所以f′(1)=f′(1)+2﹣2f(0),即f(0)=1.又,
所以f′(1)=2e2,所以f(x)=e2x+x2﹣2x.
(2)∵f(x)=e2x﹣2x+x2,
∴,
∴g′(x)=ex﹣a.
①当a≤0时,g′(x)>0,函数f(x)在R上单调递增;
②当a>0时,由g′(x)=ex﹣a=0得x=lna,
∴x∈(﹣∞,lna)时,g′(x)<0,g(x)单调递减;x∈(lna,+∞)时,g′(x)>0,g(x)单调递增.
综上,当a≤0时,函数g(x)的单调递增区间为(∞,∞);
当a>0时,函数g(x)的单调递增区间为(lna,+∞),单调递减区间为(﹣∞,lna).
(3)解:设,∵,∴p(x)在x∈[1,+∞)上为减函数,又p(e)=0,∴当1≤x≤e时,p(x)≥0,当x>e时,p(x)<0.∵,,∴q′(x)在x∈[1,+∞)上为增函数,又q′(1)=0,∴x∈[1,+∞)时,q'(x)≥0,∴q(x)在x∈[1,+∞)上为增函数,∴q(x)≥q(1)=a+1>0.
①当1≤x≤e时,,
设,则,∴m(x)在x∈[1,+∞)上为减函数,
∴m(x)≤m(1)=e﹣1﹣a,
∵a≥2,∴m(x)<0,∴|p(x)|<|q(x)|,∴比ex﹣1+a更靠近lnx.
②当x>e时,,
设n(x)=2lnx﹣ex﹣1﹣a,则,,∴n′(x)在x>e时为减函数,
∴,∴n(x)在x>e时为减函数,∴n(x)<n(e)=2﹣a﹣ee﹣1<0,
∴|p(x)|<|q(x)|,∴比ex﹣1+a更靠近lnx.
综上:在a≥2,x≥1时,比ex﹣1+a更靠近lnx.
[选修4-1:几何证明选讲]
22.如图所示,AB为圆O的直径,CB,CD为圆O的切线,B,D为切点.
(1)求证:AD∥OC;
(2)若圆O的半径为2,求AD OC的值.
【考点】相似三角形的性质.
【分析】(1)连接BD,OD,利用切线的性质,证明BD⊥OC,利用AB为直径,证明AD⊥DB,即可证明AD∥OC;
(2)证明Rt△BAD∽Rt△COB,可得,即可求AD OC的值
【解答】(1)证明:连接BD,OD,
∵CB,CD是圆O的两条切线,
∴BD⊥OC,
又AB为直径,∴AD⊥DB,
∴AD∥OC.
(2)解:∵AD∥OC,∴∠DAB=∠COB,
∴Rt△BAD∽Rt△COB,
∴,
∴AD OC=AB OB=8.
[选修4-4:坐标系与参数方程]
23.在直角坐标系xOy中,圆C的参数方程为(θ为参数).
(1)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(2)已知A(﹣2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.
【考点】简单曲线的极坐标方程;参数方程化成普通方程.
【分析】(1)圆C的参数方程为,通过三角函数的平方关系式消去参数θ,得到普通方程.通过x=ρcosθ,y=ρsinθ,得到圆C的极坐标方程.
(2)求出点M(x,y)到直线AB:x﹣y+2=0的距离,表示出△ABM的面积,通过两角和的正弦函数,结合绝对值的几何意义,求解△ABM面积的最大值.
【解答】解:(1)圆C的参数方程为(θ为参数)
所以普通方程为(x﹣3)2+(y+4)2=4.,
x=ρcosθ,y=ρsinθ,可得(ρcosθ﹣3)2+(ρsinθ+4)2=4,
化简可得圆C的极坐标方程:ρ2﹣6ρcosθ+8ρsinθ+21=0.
(2)点M(x,y)到直线AB:x﹣y+2=0的距离为
△ABM的面积
所以△ABM面积的最大值为
[选修4-5:不等式选讲]
24.(1)已知a,b都是正数,且a≠b,求证:a3+b3>a2b+ab2;
(2)已知a,b,c都是正数,求证:≥abc.
【考点】不等式的证明.
【分析】(1)由条件a≠b推出:a2﹣2ab+b2>0,通过变形,应用不等式的性质可证出结论;
(2)利用基本不等式,再相加,即可证明结论.
【解答】证明:(1)∵a≠b,∴a﹣b≠0,∴a2﹣2ab+b2>0,∴a2﹣ab+b2>ab.
而a,b均为正数,∴a+b>0,∴(a+b)(a2﹣ab+b2)>ab(a+b)
∴a3+b3>a2b+ab2
成立;
(2)∵a,b,c都是正数,
∴a2b2+b2c2≥2acb2,a2b2+c2a2≥2bca2,c2a2+b2c2≥2abc2,
三式相加可得2(a2b2+b2c2+c2a2)≥2abc(a+b+c),
∴a2b2+b2c2+c2a2)≥abc(a+b+c),
∴≥abc.
2017年2月11日
同课章节目录
