辽宁省铁岭市协作体2017届高三(上)第三次联考数学试卷(文科)(解析版)
文档属性
| 名称 | 辽宁省铁岭市协作体2017届高三(上)第三次联考数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 306.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-12 10:54:11 | ||
图片预览




文档简介
2016-2017学年辽宁省铁岭市协作体高三(上)第三次联考数学试卷(文科)
一.选择题(共12小题,每题5分)
1.已知I为全集,集合M,N I,若M∩N=N,则( )
A.
B.
C.
D.
2.若p:|x|>2,q:x>2,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.下列函数中,最小正周期为π的是( )
A.y=2sinx
B.y=cos2x
C.y=sinx
D.y=2cos(x+)
4.已知=(2,1),=(x,﹣2),且(+)∥(2﹣),则x等于( )
A.﹣6
B.6
C.﹣4
D.4
5.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,可求得该女子第3天所织布的尺数为( )
A.
B.
C.
D.
6.已知实数x、y满足约束条件,则其围成的平面区域的面积为( )
A.1
B.
C.
D.
7.0.80.7,log23,log0.32的大小关系是( )
A.log0.32<0.80.7<log23
B.0.80.7<log23<log0.32
C.0.80.7<log0.32<log23
D.log0.32<log23<0.80.7
8.函数f(x)=x﹣2lnx在区间[1,e]上的最小值和最大值分别是( )
A.1和e﹣2
B.2﹣2ln2和e﹣2
C.﹣1和e﹣2
D.2﹣2ln2和1
9.网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
A.
B.
C.
D.
10.函数y=的图象与函数y=2sinπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
A.2
B.4
C.6
D.8
11.若函数f(x)=x3﹣3x在(a,6﹣a2)上有最大值,则实数a的取值范围是( )
A.(﹣,﹣1)
B.(﹣,﹣1]
C.(﹣,﹣2)
D.(﹣,﹣2]
12.设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
二.填空题(共4小题,每题5分)
13.已知{an}为等差数列,Sn为其前n项和.若a1=6,a3+a5=0,则S6= .
14.已知向量,夹角为45°,且||=1,|2﹣|=,则||= .
15.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是 寸.
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
16.已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导数f′(x)<,则不等式f(x2)<的解集为 .
三.解答题(共7小题,17---21每题12分,22-23选择一个作答,10分)
17.已知函数f(x)=sin2x﹣cos2x.
(Ⅰ)求f(x)的最小周期和最小值;
(Ⅱ)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x∈时,求g(x)的值域.
18.等差数列{an}中,a7=4,a19=2a9,
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=,求数列{bn}的前n项和Sn.
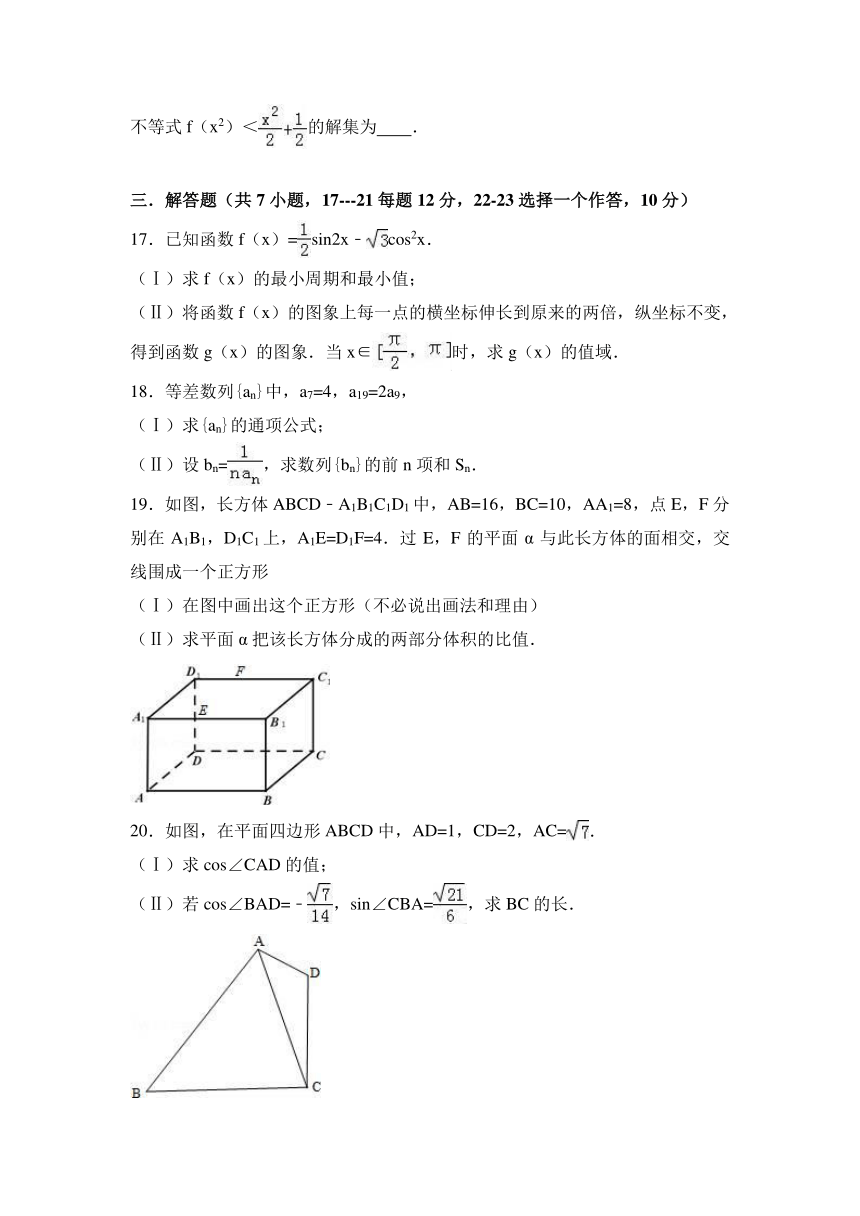
19.如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形
(Ⅰ)在图中画出这个正方形(不必说出画法和理由)
(Ⅱ)求平面α把该长方体分成的两部分体积的比值.
20.如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣,sin∠CBA=,求BC的长.
21.设f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(Ⅰ)令g(x)=f′(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值,求实数a的取值范围.
22.在平面直角坐标系xOy中,曲线C1:(φ为参数,实数a>0),曲线C2:(φ为参数,实数b>0).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α(ρ≥0,0≤α≤)与C1交于O、A两点,与C2交于O、B两点.当α=0时,|OA|=1;当α=时,|OB|=2.
(Ⅰ)求a,b的值;
(Ⅱ)求2|OA|2+|OA| |OB|的最大值.
23.设函数f(x)=|x+|+|x﹣a|(a>0).
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若f(3)<5,求a的取值范围.
2016-2017学年辽宁省铁岭市协作体高三(上)第三次联考数学试卷(文科)
参考答案与试题解析
一.选择题(共12小题,每题5分)
1.已知I为全集,集合M,N I,若M∩N=N,则( )
A.
B.
C.
D.
【考点】集合的包含关系判断及应用.
【分析】根据题意,做出图示,依次分析选项可得答案.
【解答】解:根据题意,若M∩N=N,则N M,
做出图示如图,
分析可得,必有,
故选C.
2.若p:|x|>2,q:x>2,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】充要条件.
【分析】由|x|>2,得x>2或x<﹣2.故x>2是x>2或x<﹣2成立的充分不必要条件,即p是q成立的必要不充分条件.
【解答】解:∵|x|>2∴x>2或x<﹣2.
故x>2是x>2或x<﹣2成立的充分不必要条件,
即p是q成立的必要不充分条件.
故选B.
3.下列函数中,最小正周期为π的是( )
A.y=2sinx
B.y=cos2x
C.y=sinx
D.y=2cos(x+)
【考点】三角函数的周期性及其求法.
【分析】直接求出各个函数的周期,判断满足题意选项即可.
【解答】解:y=2sinx的最小正周期为2π,不满足题意;
y=cos2x的最小正周期是π,满足题意;
y=sinx的最小正周期是=4π,不满足题意;
y=2cos(x+)的最小正周期是2π不满足题意;
故选:B.
4.已知=(2,1),=(x,﹣2),且(+)∥(2﹣),则x等于( )
A.﹣6
B.6
C.﹣4
D.4
【考点】平行向量与共线向量.
【分析】求出向量,利用两个向量共线求出x即可.
【解答】解:∵=(2,1),=(x,﹣2),
∴+=(2+x,﹣1)
2﹣=(4﹣x,4),
∵(+)∥(2﹣),
∴8+4x=﹣4+x,解得x=﹣4.
故选:C.
5.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,可求得该女子第3天所织布的尺数为( )
A.
B.
C.
D.
【考点】等比数列的前n项和.
【分析】设这女子每天分别织布an尺,则数列{an}是等比数列,公比q=2.利用等比数列的通项公式及其前n项公式即可得出.
【解答】解:设这女子每天分别织布an尺,
则数列{an}是等比数列,公比q=2.
则=5,解得.
∴a3==.
故选:A.
6.已知实数x、y满足约束条件,则其围成的平面区域的面积为( )
A.1
B.
C.
D.
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,根据平面区域即可求出面积.
【解答】解:作出不等式组对应的平面区域如图:
则对应的区域为△ABC,
其中A(1,0),B(2,0),
由,解得,即C(,),
则△ABC的面积S==,
故选:D.
7.0.80.7,log23,log0.32的大小关系是( )
A.log0.32<0.80.7<log23
B.0.80.7<log23<log0.32
C.0.80.7<log0.32<log23
D.log0.32<log23<0.80.7
【考点】对数值大小的比较.
【分析】依据对数的性质,指数的性质,分别确定0.80.7,log23,log0.32的数值的范围,然后判定选项.
【解答】解:因为0.80.7∈(0,1);log23>1;log0.32<0
所以log0.32<0.80.7<log23
故选A.
8.函数f(x)=x﹣2lnx在区间[1,e]上的最小值和最大值分别是( )
A.1和e﹣2
B.2﹣2ln2和e﹣2
C.﹣1和e﹣2
D.2﹣2ln2和1
【考点】利用导数求闭区间上函数的最值.
【分析】求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值和最小值即可.
【解答】解:f(x)=x﹣2lnx,f′(x)=1﹣=,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,
∴f(x)在[1,2)递减,在(2,e]递增,
∴f(x)min=f(2)=2﹣2ln2,而f(1)=1>f(e)=e﹣2,
故f(x)在区间[1,e]上的最小值和最大值分别是:2﹣2ln2,1,
故选:D.
9.网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
A.
B.
C.
D.
【考点】由三视图求面积、体积.
【分析】该几何体是有一个侧面PAC垂直于底面,高为,底面是一个等腰直角三角形的三棱锥,这个几何体的外接球的球心O在高线PD上,且是等边三角形PAC的中心,由此能求出这个几何体的外接球的半径R,从而能求出这个几何体的外接球的表面积.
【解答】解:由已知中正视图是一个正三角形,侧视图和俯视图均为三角形,
可得该几何体是有一个侧面PAC垂直于底面,高为,
底面是一个等腰直角三角形的三棱锥,如图.
则这个几何体的外接球的球心O在高线PD上,
且是等边三角形PAC的中心,
这个几何体的外接球的半径R=PD=.
则这个几何体的外接球的表面积为S=4πR2=4π×()2=.
故选:D.
10.函数y=的图象与函数y=2sinπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
A.2
B.4
C.6
D.8
【考点】奇偶函数图象的对称性;三角函数的周期性及其求法;正弦函数的图象.
【分析】的图象由奇函数的图象向右平移1个单位而得,所以它的图象关于点(1,0)中心对称,再由正弦函数的对称中心公式,可得函数y2=2sinπx的图象的一个对称中心也是点(1,0),故交点个数为偶数,且每一对对称点的横坐标之和为2.由此不难得到正确答案.
【解答】解:函数,y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象如图
当1<x≤4时,y1<0
而函数y2在(1,4)上出现1.5个周期的图象,
在和上是减函数;
在和上是增函数.
∴函数y1在(1,4)上函数值为负数,且与y2的图象有四个交点E、F、G、H
相应地,y1在(﹣2,1)上函数值为正数,且与y2的图象有四个交点A、B、C、D
且:xA+xH=xB+xG═xC+xF=xD+xE=2,故所求的横坐标之和为8
故选D
11.若函数f(x)=x3﹣3x在(a,6﹣a2)上有最大值,则实数a的取值范围是( )
A.(﹣,﹣1)
B.(﹣,﹣1]
C.(﹣,﹣2)
D.(﹣,﹣2]
【考点】利用导数求闭区间上函数的最值.
【分析】因为给的是开区间,最大值一定是在该极大值点处取得,因此对原函数求导、求极大值点,求出函数极大值时的x值,然后让极大值点落在区间(a,6﹣a2)内,依此构造不等式.即可求解实数a的值.
【解答】解:由题意f(x)=x3﹣3x,
所以f′(x)=3x2﹣3=3(x+1)(x﹣1),
当x<﹣1或x>1时,f′(x)>0;
当﹣1<x<1时,f′(x)<0,故x=﹣1是函数f(x)的极大值点,f(﹣1)=﹣1+3=2.,x3﹣3x=2,解得x=2,
所以由题意应有:,
解得﹣<a≤2.
故选:D.
12.设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
【考点】导数的运算.
【分析】令g(x)=f(x)﹣x2,由g(﹣x)+g(x)=0,可得函数g(x)为奇函数.利用导数可得函数g(x)在R上是增函数,f(2﹣a)﹣f(a)≥2﹣2a,即g(2﹣a)≥g(a),可得
2﹣a≥a,由此解得a的范围.
【解答】解:∵f(﹣x)+f(x)=x2,∴f(x)﹣x2
+f(﹣x)﹣x2
=0,
令g(x)=f(x)﹣x2,∵g(﹣x)+g(x)=f(﹣x)﹣x2+f(x)﹣x2=0,
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,f′(x)>x.
∴x∈(0,+∞)时,g′(x)=f′(x)﹣x>0,故函数g(x)在(0,+∞)上是增函数,
故函数g(x)在(﹣∞,0)上也是增函数,由f(0)=0,可得g(x)在R上是增函数.
f(2﹣a)﹣f(a)≥2﹣2a,等价于f(2﹣a)﹣≥f(a)﹣,
即g(2﹣a)≥g(a),∴2﹣a≥a,解得a≤1,
故选:B.
二.填空题(共4小题,每题5分)
13.已知{an}为等差数列,Sn为其前n项和.若a1=6,a3+a5=0,则S6= 6 .
【考点】等差数列的前n项和.
【分析】由已知条件利用等差数列的性质求出公差,由此利用等差数列的前n项和公式能求出S6.
【解答】解:∵{an}为等差数列,Sn为其前n项和.
a1=6,a3+a5=0,
∴a1+2d+a1+4d=0,
∴12+6d=0,
解得d=﹣2,
∴S6==36﹣30=6.
故答案为:6.
14.已知向量,夹角为45°,且||=1,|2﹣|=,则||= .
【考点】平面向量数量积的运算.
【分析】利用数量积的性质即可得出.
【解答】解:∵向量,夹角为45°,且||=1,|2﹣|=.
∴=,
化为=10,
化为,
∵,
解得||=.
故答案为:.
15.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是 3 寸.
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
【考点】棱柱、棱锥、棱台的体积.
【分析】由题意得到盆中水面的半径,利用圆台的体积公式求出水的体积,用水的体积除以盆的上地面面积即可得到答案.
【解答】解:如图,由题意可知,天池盆上底面半径为14寸,
下底面半径为6寸,高为18寸.
因为积水深9寸,所以水面半径为寸.
则盆中水的体积为(立方寸).
所以则平地降雨量等于(寸).
故答案为3.
16.已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导数f′(x)<,则不等式f(x2)<的解集为 (﹣∞,﹣1)∪(1,+∞) .
【考点】导数的运算;其他不等式的解法.
【分析】设F(x)=f(x)﹣x,根据题意可得函数F(x)在R上单调递减,然后根据f(x2)<可得f(x2)﹣<f(1)﹣,最后根据单调性可求出x的取值范围.
【解答】解:设F(x)=f(x)﹣x,则F′(x)=f′(x)﹣
∵f′(x)<,∴F′(x)=f′(x)﹣<0
即函数F(x)在R上单调递减
而f(x2)<即f(x2)﹣<f(1)﹣
∴F(x2)<F(1)而函数F(x)在R上单调递减
∴x2>1即x∈(﹣∞,﹣1)∪(1,+∞)
故答案为:(﹣∞,﹣1)∪(1,+∞)
三.解答题(共7小题,17---21每题12分,22-23选择一个作答,10分)
17.已知函数f(x)=sin2x﹣cos2x.
(Ⅰ)求f(x)的最小周期和最小值;
(Ⅱ)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x∈时,求g(x)的值域.
【考点】三角函数中的恒等变换应用;函数y=Asin(ωx+φ)的图象变换.
【分析】(Ⅰ)由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x﹣)﹣,从而可求最小周期和最小值;
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换可得g(x)=sin(x﹣)﹣,由x∈[,π]时,可得x﹣的范围,即可求得g(x)的值域.
【解答】解:(Ⅰ)∵f(x)=sin2x﹣cos2x=sin2x﹣(1+cos2x)=sin(2x﹣)﹣,
∴f(x)的最小周期T==π,最小值为:﹣1﹣=﹣.
(Ⅱ)由条件可知:g(x)=sin(x﹣)﹣
当x∈[,π]时,有x﹣∈[,],从而sin(x﹣)的值域为[,1],那么sin(x﹣)﹣的值域为:[,],
故g(x)在区间[,π]上的值域是[,].
18.等差数列{an}中,a7=4,a19=2a9,
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=,求数列{bn}的前n项和Sn.
【考点】数列的求和;等差数列的通项公式.
【分析】(I)由a7=4,a19=2a9,结合等差数列的通项公式可求a1,d,进而可求an
(II)由==,利用裂项求和即可求解
【解答】解:(I)设等差数列{an}的公差为d
∵a7=4,a19=2a9,
∴
解得,a1=1,d=
∴=
(II)∵==
∴sn=
==
19.如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形
(Ⅰ)在图中画出这个正方形(不必说出画法和理由)
(Ⅱ)求平面α把该长方体分成的两部分体积的比值.
【考点】棱柱、棱锥、棱台的体积;平面的基本性质及推论.
【分析】(Ⅰ)利用平面与平面平行的性质,可在图中画出这个正方形;
(Ⅱ)求出MH==6,AH=10,HB=6,即可求平面a把该长方体分成的两部分体积的比值.
【解答】解:(Ⅰ)交线围成的正方形EFGH如图所示;
(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.
因为EFGH为正方形,所以EH=EF=BC=10,
于是MH==6,AH=10,HB=6.
因为长方体被平面α分成两个高为10的直棱柱,
所以其体积的比值为.
20.如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣,sin∠CBA=,求BC的长.
【考点】解三角形的实际应用.
【分析】(Ⅰ)利用余弦定理,利用已知条件求得cos∠CAD的值.
(Ⅱ)根据cos∠CAD,cos∠BAD的值分别,求得sin∠BAD和sin∠CAD,进而利用两角和公式求得sin∠BAC的值,最后利用正弦定理求得BC.
【解答】解:(Ⅰ)cos∠CAD===.
(Ⅱ)∵cos∠BAD=﹣,
∴sin∠BAD==,
∵cos∠CAD=,
∴sin∠CAD==
∴sin∠BAC=sin(∠BAD﹣∠CAD)=sin∠BADcos∠CAD﹣cos∠BADsin∠CAD=×+×=,
∴由正弦定理知=,
∴BC= sin∠BAC=×=3
21.设f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(Ⅰ)令g(x)=f′(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值,求实数a的取值范围.
【考点】利用导数研究函数的单调性;利用导数研究函数的极值.
【分析】(Ⅰ)先求出g(x)=f′(x)的解析式,然后求函数的导数g′(x),利用函数单调性和导数之间的关系即可求g(x)的单调区间;
(Ⅱ)分别讨论a的取值范围,根据函数极值的定义,进行验证即可得到结论.
【解答】解:(Ⅰ)∵f(x)=xlnx﹣ax2+(2a﹣1)x,
∴g(x)=f′(x)=lnx﹣2ax+2a,x>0,
g′(x)=﹣2a=,
当a≤0,g′(x)>0恒成立,即可g(x)的单调增区间是(0,+∞);
当a>0,当x>时,g′(x)<0,函数为减函数,
当0<x<,g′(x)>0,函数为增函数,
∴当a≤0时,g(x)的单调增区间是(0,+∞);
当a>0时,g(x)的单调增区间是(0,),单调减区间是(,+∞);
(Ⅱ)∵f(x)在x=1处取得极大值,∴f′(1)=0,
①当a≤0时,f′(x)单调递增,
则当0<x<1时,f′(x)<0,f(x)单调递减,
当x>1时,f′(x)>0,f(x)单调递增,∴f(x)在x=1处取得极小值,不合题意,
②当0<a<时,>1,由(1)知,f′(x)在(0,)内单调递增,
当0<x<1时,f′(x)<0,当1<x<时,f′(x)>0,
∴f(x)在(0,1)内单调递减,在(1,)内单调递增,即f(x)在x=1处取得极小值,不合题意.
③当a=时,
=1,f′(x)在(0,1)内单调递增,在(1,+∞)上单调递减,
则当x>0时,f′(x)≤0,f(x)单调递减,不合题意.
④当a>时,0<<1,
当<x<1时,f′(x)>0,f(x)单调递增,当x>1时,f′(x)<0,f(x)单调递减,
∴当x=1时,f(x)取得极大值,满足条件.
综上实数a的取值范围是a>.
22.在平面直角坐标系xOy中,曲线C1:(φ为参数,实数a>0),曲线C2:(φ为参数,实数b>0).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α(ρ≥0,0≤α≤)与C1交于O、A两点,与C2交于O、B两点.当α=0时,|OA|=1;当α=时,|OB|=2.
(Ⅰ)求a,b的值;
(Ⅱ)求2|OA|2+|OA| |OB|的最大值.
【考点】参数方程化成普通方程;简单曲线的极坐标方程.
【分析】(I)由曲线C1:(φ为参数,实数a>0),利用cos2φ+sin2φ=1即可化为普通方程,再利用极坐标与直角坐标互化公式即可得出极坐标方程,进而得出a的值.同理可得b的值.
(II)由(I)可得C1,C2的方程分别为ρ=cosθ,ρ=2sinθ.可得2|OA|2+|OA| |OB|=2cos2θ+2sinθcosθ=+1,利用三角函数的单调性与值域即可得出.
【解答】解:(Ⅰ)由曲线C1:(φ为参数,实数a>0),
化为普通方程为(x﹣a)2+y2=a2,展开为:x2+y2﹣2ax=0,
其极坐标方程为ρ2=2aρcosθ,即ρ=2acosθ,由题意可得当θ=0时,|OA|=ρ=1,∴a=.
曲线C2:(φ为参数,实数b>0),
化为普通方程为x2+(y﹣b)2=b2,展开可得极坐标方程为ρ=2bsinθ,
由题意可得当时,|OB|=ρ=2,∴b=1.
(Ⅱ)由(I)可得C1,C2的方程分别为ρ=cosθ,ρ=2sinθ.
∴2|OA|2+|OA| |OB|=2cos2θ+2sinθcosθ=sin2θ+cos2θ+1=+1,
∵2θ+∈,∴+1的最大值为+1,
当2θ+=时,θ=时取到最大值.
23.设函数f(x)=|x+|+|x﹣a|(a>0).
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若f(3)<5,求a的取值范围.
【考点】绝对值不等式的解法.
【分析】(Ⅰ)由a>0,f(x)=|x+|+|x﹣a|,利用绝对值三角不等式、基本不等式证得f(x)≥2成立.
(Ⅱ)由f(3)=|3+|+|3﹣a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.
【解答】解:(Ⅰ)证明:∵a>0,f(x)=|x+|+|x﹣a|≥|(x+)﹣(x﹣a)|=|a+|=a+≥2=2,
故不等式f(x)≥2成立.
(Ⅱ)∵f(3)=|3+|+|3﹣a|<5,
∴当a>3时,不等式即a+<5,即a2﹣5a+1<0,解得3<a<.
当0<a≤3时,不等式即
6﹣a+<5,即
a2﹣a﹣1>0,求得<a≤3.
综上可得,a的取值范围(,).
2017年2月11日
一.选择题(共12小题,每题5分)
1.已知I为全集,集合M,N I,若M∩N=N,则( )
A.
B.
C.
D.
2.若p:|x|>2,q:x>2,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.下列函数中,最小正周期为π的是( )
A.y=2sinx
B.y=cos2x
C.y=sinx
D.y=2cos(x+)
4.已知=(2,1),=(x,﹣2),且(+)∥(2﹣),则x等于( )
A.﹣6
B.6
C.﹣4
D.4
5.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,可求得该女子第3天所织布的尺数为( )
A.
B.
C.
D.
6.已知实数x、y满足约束条件,则其围成的平面区域的面积为( )
A.1
B.
C.
D.
7.0.80.7,log23,log0.32的大小关系是( )
A.log0.32<0.80.7<log23
B.0.80.7<log23<log0.32
C.0.80.7<log0.32<log23
D.log0.32<log23<0.80.7
8.函数f(x)=x﹣2lnx在区间[1,e]上的最小值和最大值分别是( )
A.1和e﹣2
B.2﹣2ln2和e﹣2
C.﹣1和e﹣2
D.2﹣2ln2和1
9.网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
A.
B.
C.
D.
10.函数y=的图象与函数y=2sinπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
A.2
B.4
C.6
D.8
11.若函数f(x)=x3﹣3x在(a,6﹣a2)上有最大值,则实数a的取值范围是( )
A.(﹣,﹣1)
B.(﹣,﹣1]
C.(﹣,﹣2)
D.(﹣,﹣2]
12.设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
二.填空题(共4小题,每题5分)
13.已知{an}为等差数列,Sn为其前n项和.若a1=6,a3+a5=0,则S6= .
14.已知向量,夹角为45°,且||=1,|2﹣|=,则||= .
15.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是 寸.
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
16.已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导数f′(x)<,则不等式f(x2)<的解集为 .
三.解答题(共7小题,17---21每题12分,22-23选择一个作答,10分)
17.已知函数f(x)=sin2x﹣cos2x.
(Ⅰ)求f(x)的最小周期和最小值;
(Ⅱ)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x∈时,求g(x)的值域.
18.等差数列{an}中,a7=4,a19=2a9,
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=,求数列{bn}的前n项和Sn.
19.如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形
(Ⅰ)在图中画出这个正方形(不必说出画法和理由)
(Ⅱ)求平面α把该长方体分成的两部分体积的比值.
20.如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣,sin∠CBA=,求BC的长.
21.设f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(Ⅰ)令g(x)=f′(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值,求实数a的取值范围.
22.在平面直角坐标系xOy中,曲线C1:(φ为参数,实数a>0),曲线C2:(φ为参数,实数b>0).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α(ρ≥0,0≤α≤)与C1交于O、A两点,与C2交于O、B两点.当α=0时,|OA|=1;当α=时,|OB|=2.
(Ⅰ)求a,b的值;
(Ⅱ)求2|OA|2+|OA| |OB|的最大值.
23.设函数f(x)=|x+|+|x﹣a|(a>0).
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若f(3)<5,求a的取值范围.
2016-2017学年辽宁省铁岭市协作体高三(上)第三次联考数学试卷(文科)
参考答案与试题解析
一.选择题(共12小题,每题5分)
1.已知I为全集,集合M,N I,若M∩N=N,则( )
A.
B.
C.
D.
【考点】集合的包含关系判断及应用.
【分析】根据题意,做出图示,依次分析选项可得答案.
【解答】解:根据题意,若M∩N=N,则N M,
做出图示如图,
分析可得,必有,
故选C.
2.若p:|x|>2,q:x>2,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】充要条件.
【分析】由|x|>2,得x>2或x<﹣2.故x>2是x>2或x<﹣2成立的充分不必要条件,即p是q成立的必要不充分条件.
【解答】解:∵|x|>2∴x>2或x<﹣2.
故x>2是x>2或x<﹣2成立的充分不必要条件,
即p是q成立的必要不充分条件.
故选B.
3.下列函数中,最小正周期为π的是( )
A.y=2sinx
B.y=cos2x
C.y=sinx
D.y=2cos(x+)
【考点】三角函数的周期性及其求法.
【分析】直接求出各个函数的周期,判断满足题意选项即可.
【解答】解:y=2sinx的最小正周期为2π,不满足题意;
y=cos2x的最小正周期是π,满足题意;
y=sinx的最小正周期是=4π,不满足题意;
y=2cos(x+)的最小正周期是2π不满足题意;
故选:B.
4.已知=(2,1),=(x,﹣2),且(+)∥(2﹣),则x等于( )
A.﹣6
B.6
C.﹣4
D.4
【考点】平行向量与共线向量.
【分析】求出向量,利用两个向量共线求出x即可.
【解答】解:∵=(2,1),=(x,﹣2),
∴+=(2+x,﹣1)
2﹣=(4﹣x,4),
∵(+)∥(2﹣),
∴8+4x=﹣4+x,解得x=﹣4.
故选:C.
5.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,可求得该女子第3天所织布的尺数为( )
A.
B.
C.
D.
【考点】等比数列的前n项和.
【分析】设这女子每天分别织布an尺,则数列{an}是等比数列,公比q=2.利用等比数列的通项公式及其前n项公式即可得出.
【解答】解:设这女子每天分别织布an尺,
则数列{an}是等比数列,公比q=2.
则=5,解得.
∴a3==.
故选:A.
6.已知实数x、y满足约束条件,则其围成的平面区域的面积为( )
A.1
B.
C.
D.
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,根据平面区域即可求出面积.
【解答】解:作出不等式组对应的平面区域如图:
则对应的区域为△ABC,
其中A(1,0),B(2,0),
由,解得,即C(,),
则△ABC的面积S==,
故选:D.
7.0.80.7,log23,log0.32的大小关系是( )
A.log0.32<0.80.7<log23
B.0.80.7<log23<log0.32
C.0.80.7<log0.32<log23
D.log0.32<log23<0.80.7
【考点】对数值大小的比较.
【分析】依据对数的性质,指数的性质,分别确定0.80.7,log23,log0.32的数值的范围,然后判定选项.
【解答】解:因为0.80.7∈(0,1);log23>1;log0.32<0
所以log0.32<0.80.7<log23
故选A.
8.函数f(x)=x﹣2lnx在区间[1,e]上的最小值和最大值分别是( )
A.1和e﹣2
B.2﹣2ln2和e﹣2
C.﹣1和e﹣2
D.2﹣2ln2和1
【考点】利用导数求闭区间上函数的最值.
【分析】求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值和最小值即可.
【解答】解:f(x)=x﹣2lnx,f′(x)=1﹣=,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,
∴f(x)在[1,2)递减,在(2,e]递增,
∴f(x)min=f(2)=2﹣2ln2,而f(1)=1>f(e)=e﹣2,
故f(x)在区间[1,e]上的最小值和最大值分别是:2﹣2ln2,1,
故选:D.
9.网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为( )
A.
B.
C.
D.
【考点】由三视图求面积、体积.
【分析】该几何体是有一个侧面PAC垂直于底面,高为,底面是一个等腰直角三角形的三棱锥,这个几何体的外接球的球心O在高线PD上,且是等边三角形PAC的中心,由此能求出这个几何体的外接球的半径R,从而能求出这个几何体的外接球的表面积.
【解答】解:由已知中正视图是一个正三角形,侧视图和俯视图均为三角形,
可得该几何体是有一个侧面PAC垂直于底面,高为,
底面是一个等腰直角三角形的三棱锥,如图.
则这个几何体的外接球的球心O在高线PD上,
且是等边三角形PAC的中心,
这个几何体的外接球的半径R=PD=.
则这个几何体的外接球的表面积为S=4πR2=4π×()2=.
故选:D.
10.函数y=的图象与函数y=2sinπx(﹣2≤x≤4)的图象所有交点的横坐标之和等于( )
A.2
B.4
C.6
D.8
【考点】奇偶函数图象的对称性;三角函数的周期性及其求法;正弦函数的图象.
【分析】的图象由奇函数的图象向右平移1个单位而得,所以它的图象关于点(1,0)中心对称,再由正弦函数的对称中心公式,可得函数y2=2sinπx的图象的一个对称中心也是点(1,0),故交点个数为偶数,且每一对对称点的横坐标之和为2.由此不难得到正确答案.
【解答】解:函数,y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象如图
当1<x≤4时,y1<0
而函数y2在(1,4)上出现1.5个周期的图象,
在和上是减函数;
在和上是增函数.
∴函数y1在(1,4)上函数值为负数,且与y2的图象有四个交点E、F、G、H
相应地,y1在(﹣2,1)上函数值为正数,且与y2的图象有四个交点A、B、C、D
且:xA+xH=xB+xG═xC+xF=xD+xE=2,故所求的横坐标之和为8
故选D
11.若函数f(x)=x3﹣3x在(a,6﹣a2)上有最大值,则实数a的取值范围是( )
A.(﹣,﹣1)
B.(﹣,﹣1]
C.(﹣,﹣2)
D.(﹣,﹣2]
【考点】利用导数求闭区间上函数的最值.
【分析】因为给的是开区间,最大值一定是在该极大值点处取得,因此对原函数求导、求极大值点,求出函数极大值时的x值,然后让极大值点落在区间(a,6﹣a2)内,依此构造不等式.即可求解实数a的值.
【解答】解:由题意f(x)=x3﹣3x,
所以f′(x)=3x2﹣3=3(x+1)(x﹣1),
当x<﹣1或x>1时,f′(x)>0;
当﹣1<x<1时,f′(x)<0,故x=﹣1是函数f(x)的极大值点,f(﹣1)=﹣1+3=2.,x3﹣3x=2,解得x=2,
所以由题意应有:,
解得﹣<a≤2.
故选:D.
12.设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(﹣x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,则实数a的取值范围为( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
【考点】导数的运算.
【分析】令g(x)=f(x)﹣x2,由g(﹣x)+g(x)=0,可得函数g(x)为奇函数.利用导数可得函数g(x)在R上是增函数,f(2﹣a)﹣f(a)≥2﹣2a,即g(2﹣a)≥g(a),可得
2﹣a≥a,由此解得a的范围.
【解答】解:∵f(﹣x)+f(x)=x2,∴f(x)﹣x2
+f(﹣x)﹣x2
=0,
令g(x)=f(x)﹣x2,∵g(﹣x)+g(x)=f(﹣x)﹣x2+f(x)﹣x2=0,
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,f′(x)>x.
∴x∈(0,+∞)时,g′(x)=f′(x)﹣x>0,故函数g(x)在(0,+∞)上是增函数,
故函数g(x)在(﹣∞,0)上也是增函数,由f(0)=0,可得g(x)在R上是增函数.
f(2﹣a)﹣f(a)≥2﹣2a,等价于f(2﹣a)﹣≥f(a)﹣,
即g(2﹣a)≥g(a),∴2﹣a≥a,解得a≤1,
故选:B.
二.填空题(共4小题,每题5分)
13.已知{an}为等差数列,Sn为其前n项和.若a1=6,a3+a5=0,则S6= 6 .
【考点】等差数列的前n项和.
【分析】由已知条件利用等差数列的性质求出公差,由此利用等差数列的前n项和公式能求出S6.
【解答】解:∵{an}为等差数列,Sn为其前n项和.
a1=6,a3+a5=0,
∴a1+2d+a1+4d=0,
∴12+6d=0,
解得d=﹣2,
∴S6==36﹣30=6.
故答案为:6.
14.已知向量,夹角为45°,且||=1,|2﹣|=,则||= .
【考点】平面向量数量积的运算.
【分析】利用数量积的性质即可得出.
【解答】解:∵向量,夹角为45°,且||=1,|2﹣|=.
∴=,
化为=10,
化为,
∵,
解得||=.
故答案为:.
15.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是 3 寸.
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)
【考点】棱柱、棱锥、棱台的体积.
【分析】由题意得到盆中水面的半径,利用圆台的体积公式求出水的体积,用水的体积除以盆的上地面面积即可得到答案.
【解答】解:如图,由题意可知,天池盆上底面半径为14寸,
下底面半径为6寸,高为18寸.
因为积水深9寸,所以水面半径为寸.
则盆中水的体积为(立方寸).
所以则平地降雨量等于(寸).
故答案为3.
16.已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导数f′(x)<,则不等式f(x2)<的解集为 (﹣∞,﹣1)∪(1,+∞) .
【考点】导数的运算;其他不等式的解法.
【分析】设F(x)=f(x)﹣x,根据题意可得函数F(x)在R上单调递减,然后根据f(x2)<可得f(x2)﹣<f(1)﹣,最后根据单调性可求出x的取值范围.
【解答】解:设F(x)=f(x)﹣x,则F′(x)=f′(x)﹣
∵f′(x)<,∴F′(x)=f′(x)﹣<0
即函数F(x)在R上单调递减
而f(x2)<即f(x2)﹣<f(1)﹣
∴F(x2)<F(1)而函数F(x)在R上单调递减
∴x2>1即x∈(﹣∞,﹣1)∪(1,+∞)
故答案为:(﹣∞,﹣1)∪(1,+∞)
三.解答题(共7小题,17---21每题12分,22-23选择一个作答,10分)
17.已知函数f(x)=sin2x﹣cos2x.
(Ⅰ)求f(x)的最小周期和最小值;
(Ⅱ)将函数f(x)的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变,得到函数g(x)的图象.当x∈时,求g(x)的值域.
【考点】三角函数中的恒等变换应用;函数y=Asin(ωx+φ)的图象变换.
【分析】(Ⅰ)由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x﹣)﹣,从而可求最小周期和最小值;
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换可得g(x)=sin(x﹣)﹣,由x∈[,π]时,可得x﹣的范围,即可求得g(x)的值域.
【解答】解:(Ⅰ)∵f(x)=sin2x﹣cos2x=sin2x﹣(1+cos2x)=sin(2x﹣)﹣,
∴f(x)的最小周期T==π,最小值为:﹣1﹣=﹣.
(Ⅱ)由条件可知:g(x)=sin(x﹣)﹣
当x∈[,π]时,有x﹣∈[,],从而sin(x﹣)的值域为[,1],那么sin(x﹣)﹣的值域为:[,],
故g(x)在区间[,π]上的值域是[,].
18.等差数列{an}中,a7=4,a19=2a9,
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=,求数列{bn}的前n项和Sn.
【考点】数列的求和;等差数列的通项公式.
【分析】(I)由a7=4,a19=2a9,结合等差数列的通项公式可求a1,d,进而可求an
(II)由==,利用裂项求和即可求解
【解答】解:(I)设等差数列{an}的公差为d
∵a7=4,a19=2a9,
∴
解得,a1=1,d=
∴=
(II)∵==
∴sn=
==
19.如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形
(Ⅰ)在图中画出这个正方形(不必说出画法和理由)
(Ⅱ)求平面α把该长方体分成的两部分体积的比值.
【考点】棱柱、棱锥、棱台的体积;平面的基本性质及推论.
【分析】(Ⅰ)利用平面与平面平行的性质,可在图中画出这个正方形;
(Ⅱ)求出MH==6,AH=10,HB=6,即可求平面a把该长方体分成的两部分体积的比值.
【解答】解:(Ⅰ)交线围成的正方形EFGH如图所示;
(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.
因为EFGH为正方形,所以EH=EF=BC=10,
于是MH==6,AH=10,HB=6.
因为长方体被平面α分成两个高为10的直棱柱,
所以其体积的比值为.
20.如图,在平面四边形ABCD中,AD=1,CD=2,AC=.
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣,sin∠CBA=,求BC的长.
【考点】解三角形的实际应用.
【分析】(Ⅰ)利用余弦定理,利用已知条件求得cos∠CAD的值.
(Ⅱ)根据cos∠CAD,cos∠BAD的值分别,求得sin∠BAD和sin∠CAD,进而利用两角和公式求得sin∠BAC的值,最后利用正弦定理求得BC.
【解答】解:(Ⅰ)cos∠CAD===.
(Ⅱ)∵cos∠BAD=﹣,
∴sin∠BAD==,
∵cos∠CAD=,
∴sin∠CAD==
∴sin∠BAC=sin(∠BAD﹣∠CAD)=sin∠BADcos∠CAD﹣cos∠BADsin∠CAD=×+×=,
∴由正弦定理知=,
∴BC= sin∠BAC=×=3
21.设f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(Ⅰ)令g(x)=f′(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值,求实数a的取值范围.
【考点】利用导数研究函数的单调性;利用导数研究函数的极值.
【分析】(Ⅰ)先求出g(x)=f′(x)的解析式,然后求函数的导数g′(x),利用函数单调性和导数之间的关系即可求g(x)的单调区间;
(Ⅱ)分别讨论a的取值范围,根据函数极值的定义,进行验证即可得到结论.
【解答】解:(Ⅰ)∵f(x)=xlnx﹣ax2+(2a﹣1)x,
∴g(x)=f′(x)=lnx﹣2ax+2a,x>0,
g′(x)=﹣2a=,
当a≤0,g′(x)>0恒成立,即可g(x)的单调增区间是(0,+∞);
当a>0,当x>时,g′(x)<0,函数为减函数,
当0<x<,g′(x)>0,函数为增函数,
∴当a≤0时,g(x)的单调增区间是(0,+∞);
当a>0时,g(x)的单调增区间是(0,),单调减区间是(,+∞);
(Ⅱ)∵f(x)在x=1处取得极大值,∴f′(1)=0,
①当a≤0时,f′(x)单调递增,
则当0<x<1时,f′(x)<0,f(x)单调递减,
当x>1时,f′(x)>0,f(x)单调递增,∴f(x)在x=1处取得极小值,不合题意,
②当0<a<时,>1,由(1)知,f′(x)在(0,)内单调递增,
当0<x<1时,f′(x)<0,当1<x<时,f′(x)>0,
∴f(x)在(0,1)内单调递减,在(1,)内单调递增,即f(x)在x=1处取得极小值,不合题意.
③当a=时,
=1,f′(x)在(0,1)内单调递增,在(1,+∞)上单调递减,
则当x>0时,f′(x)≤0,f(x)单调递减,不合题意.
④当a>时,0<<1,
当<x<1时,f′(x)>0,f(x)单调递增,当x>1时,f′(x)<0,f(x)单调递减,
∴当x=1时,f(x)取得极大值,满足条件.
综上实数a的取值范围是a>.
22.在平面直角坐标系xOy中,曲线C1:(φ为参数,实数a>0),曲线C2:(φ为参数,实数b>0).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α(ρ≥0,0≤α≤)与C1交于O、A两点,与C2交于O、B两点.当α=0时,|OA|=1;当α=时,|OB|=2.
(Ⅰ)求a,b的值;
(Ⅱ)求2|OA|2+|OA| |OB|的最大值.
【考点】参数方程化成普通方程;简单曲线的极坐标方程.
【分析】(I)由曲线C1:(φ为参数,实数a>0),利用cos2φ+sin2φ=1即可化为普通方程,再利用极坐标与直角坐标互化公式即可得出极坐标方程,进而得出a的值.同理可得b的值.
(II)由(I)可得C1,C2的方程分别为ρ=cosθ,ρ=2sinθ.可得2|OA|2+|OA| |OB|=2cos2θ+2sinθcosθ=+1,利用三角函数的单调性与值域即可得出.
【解答】解:(Ⅰ)由曲线C1:(φ为参数,实数a>0),
化为普通方程为(x﹣a)2+y2=a2,展开为:x2+y2﹣2ax=0,
其极坐标方程为ρ2=2aρcosθ,即ρ=2acosθ,由题意可得当θ=0时,|OA|=ρ=1,∴a=.
曲线C2:(φ为参数,实数b>0),
化为普通方程为x2+(y﹣b)2=b2,展开可得极坐标方程为ρ=2bsinθ,
由题意可得当时,|OB|=ρ=2,∴b=1.
(Ⅱ)由(I)可得C1,C2的方程分别为ρ=cosθ,ρ=2sinθ.
∴2|OA|2+|OA| |OB|=2cos2θ+2sinθcosθ=sin2θ+cos2θ+1=+1,
∵2θ+∈,∴+1的最大值为+1,
当2θ+=时,θ=时取到最大值.
23.设函数f(x)=|x+|+|x﹣a|(a>0).
(Ⅰ)证明:f(x)≥2;
(Ⅱ)若f(3)<5,求a的取值范围.
【考点】绝对值不等式的解法.
【分析】(Ⅰ)由a>0,f(x)=|x+|+|x﹣a|,利用绝对值三角不等式、基本不等式证得f(x)≥2成立.
(Ⅱ)由f(3)=|3+|+|3﹣a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.
【解答】解:(Ⅰ)证明:∵a>0,f(x)=|x+|+|x﹣a|≥|(x+)﹣(x﹣a)|=|a+|=a+≥2=2,
故不等式f(x)≥2成立.
(Ⅱ)∵f(3)=|3+|+|3﹣a|<5,
∴当a>3时,不等式即a+<5,即a2﹣5a+1<0,解得3<a<.
当0<a≤3时,不等式即
6﹣a+<5,即
a2﹣a﹣1>0,求得<a≤3.
综上可得,a的取值范围(,).
2017年2月11日
同课章节目录
