鲁教版五四制七年级上数学当堂达标测试4.1无理数(解析版)
文档属性
| 名称 | 鲁教版五四制七年级上数学当堂达标测试4.1无理数(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 309.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-12 00:00:00 | ||
图片预览



文档简介
〖鲁教版五四制七年级上数学当堂达标〗
4.1无理数
班级:
姓名:
一、选择题:
1. 下列说法中,正确的是(
)
A.
无限不循环小数都是无理数
B.
带根号的数都是无理数
C.
无理数都是带根号的数
D.
无限小数都是无理数
2.(2016广西省贺州市)下列实数中,属于有理数的是( )
A.
B.
C.π
D.
3.下列说法中,正确的是(
)
A.
无理数的相反数还是无理数
B.
不循环小数是无理数
C.
带分数线的数一定是分数
D.
无理数包括正无理数、零、负无理数
4.
不是(
)A.
负数
B.
无理数
C.
分数
D.
小数
5. 下列各数是无理数的是(
)
A.
面积是16的正方形的边长
B.
两直角边分别为7和24的直角三角形的边长
C.
-0.1123583145……(第3个数为前两个数的和,若和为两位数,则仅取个位数)D.
6. (2016贵州省毕节市题)估计的值在(
)
A.2到3之间
B.3到4之间
C.4到5之间
D.5到6之间
二、填空题
7.
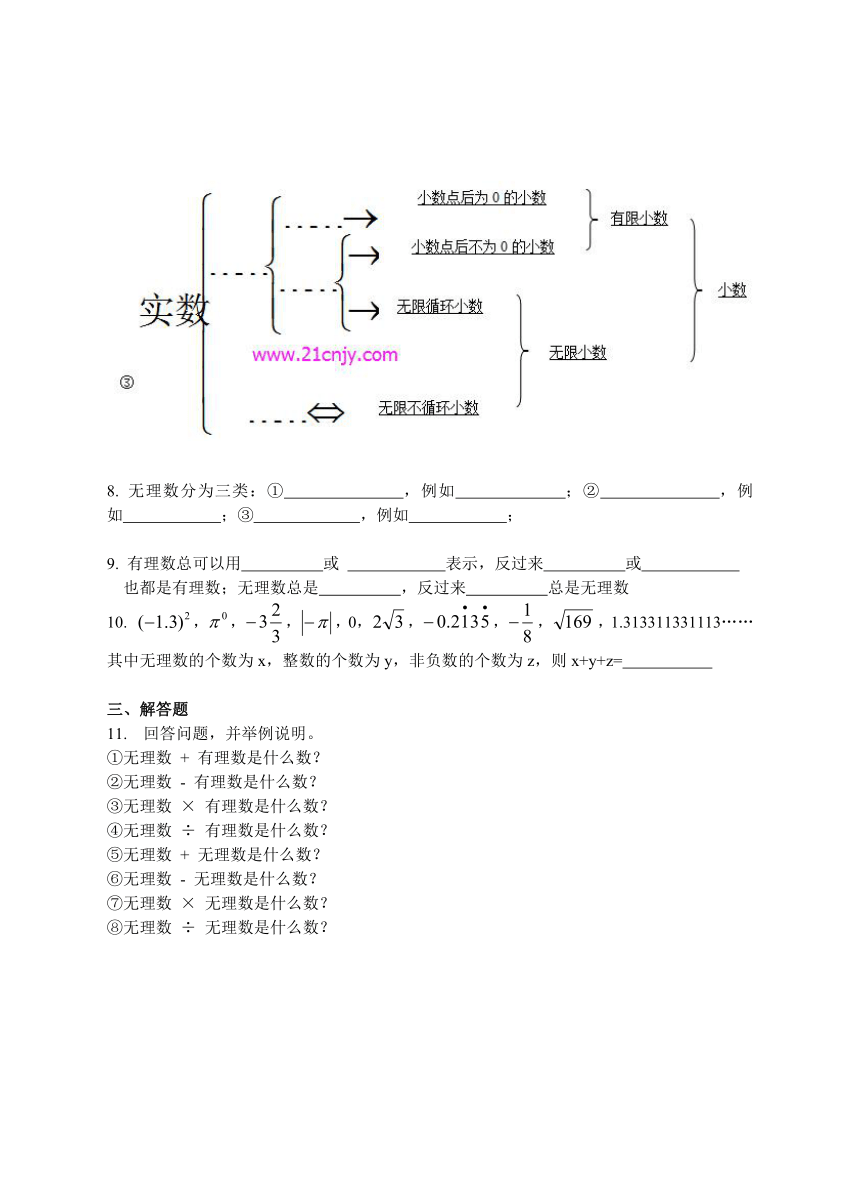
实数的分类:
①
②
8.
无理数分为三类:①
,例如
;②
,例如
;③
,例如
;
9.
有理数总可以用
或
表示,反过来
或
也都是有理数;无理数总是
,反过来
总是无理数
10.
,,,,0,,,,,1.313311331113……其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=
解答题
11.
回答问题,并举例说明。
①无理数
+
有理数是什么数?
②无理数
-
有理数是什么数?
③无理数
×
有理数是什么数?
④无理数
÷
有理数是什么数?
⑤无理数
+
无理数是什么数?
⑥无理数
-
无理数是什么数?
⑦无理数
×
无理数是什么数?
⑧无理数
÷
无理数是什么数?
12.
一个正方形的边长为m,面积为5,求代数式的值。
13.
小明在地面上画了一条数轴,原点为O,用铁丝以O点为圆心,以单位长1为半径制作一个圆环,再拉直圆环,变成一条线段,最后从O点起以此线段截得点A,则A点表示哪一个数?
14.
设面积为的圆半径为.
①是有理数吗?请说明理由。
②请估计的整数部分是几?
③将保留到千分位是几?
15.
如图,把16个边长为1的正方形拼在一起,试解决下列问题:
①连接A到D,C,D的线段,哪几条是无理数?
②是什么三角形,为什么?
〖鲁教版五四制七年级上数学当堂达标〗
4.1无理数
4.【答案】:C
【解析】:π是无限不循环小数,除以3还是无限不循环小数,故是无限不循环小数,不是分数
故选C
5.【答案】:C
【解析】:
面积是16的正方形的边长是4,是有理数
两直角边分别为7和24的直角三角形的边长是25,是有理数
C.
-0.1123583145……(第3个数为前两个数的和,若和为两位数,则仅取个位数)是无理数
D.,是有理数
故选C
6.【答案】:B
【解析】:
试题分析:因为2<<3,所以,3<+1<4,选B
考点:实数的估算
二、填空题
7.【答案】:见解析
【解析】:
①
②
8.【答案】:见解析
【解析】:无理数分为三类:①有一定结构的无限小数,如0.102100210002……②特定意义的数,如π及含π的数③带根号并且开方开不尽的数,如
9.【答案】:见解析
【解析】:有理数总可以用
有限小数
或
无限循环小数表示,反过来
有限小数或
无限循环小数
也都是有理数;无理数总是
无限不循环小数
,反过来
无限不循环小数总是无理数
10.【答案】:13
【解析】:,,,,0,,,,,1.313311331113……其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=
,,1.313311331113……是无理数,所以x=3
,0,是整数,所以y=3
,,,0,,,1.313311331113……是非负数,所以z=7
所以x+y+z=13
三、解答题
11.【答案】:见解析
【解析】:①无理数
+
有理数是无理数,如
②无理数
-
有理数是无理数数,如
③无理数
×
有理数是无理数,如
④无理数
÷
有理数是无理数,如
⑤无理数
+
无理数可能是无理数,如,无理数
+
无理数也可能是有理数,如
⑥无理数
-
无理数可能是无理数,如,无理数
-
无理数也可能是有理数,如
⑦无理数
×
无理数可能是无理数,如
⑧无理数
÷
无理数是什么数?
12.【答案】:-4
【解析】:
∵一个正方形的边长为m,面积为5
∴,
∴
【答案】:
2π或-2π
【解析】:
∵以单位长1为半径制作一个圆环
∴圆环的周长=2π
∴OA=2π,
∵点A的位置如图所示
∴A点表示2π或-2π
14.【答案】:见解析
【解析】:
①∵面积为的圆半径为
∴
∵
∴
∵若是分数,则也是分数,所以不可能是分数
∴所以不可能是有理数
②
③∵
∴=2.4……
∵
∴=2.44……
∵
∴=2.449……
=2.449或2.450
4.1无理数
班级:
姓名:
一、选择题:
1. 下列说法中,正确的是(
)
A.
无限不循环小数都是无理数
B.
带根号的数都是无理数
C.
无理数都是带根号的数
D.
无限小数都是无理数
2.(2016广西省贺州市)下列实数中,属于有理数的是( )
A.
B.
C.π
D.
3.下列说法中,正确的是(
)
A.
无理数的相反数还是无理数
B.
不循环小数是无理数
C.
带分数线的数一定是分数
D.
无理数包括正无理数、零、负无理数
4.
不是(
)A.
负数
B.
无理数
C.
分数
D.
小数
5. 下列各数是无理数的是(
)
A.
面积是16的正方形的边长
B.
两直角边分别为7和24的直角三角形的边长
C.
-0.1123583145……(第3个数为前两个数的和,若和为两位数,则仅取个位数)D.
6. (2016贵州省毕节市题)估计的值在(
)
A.2到3之间
B.3到4之间
C.4到5之间
D.5到6之间
二、填空题
7.
实数的分类:
①
②
8.
无理数分为三类:①
,例如
;②
,例如
;③
,例如
;
9.
有理数总可以用
或
表示,反过来
或
也都是有理数;无理数总是
,反过来
总是无理数
10.
,,,,0,,,,,1.313311331113……其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=
解答题
11.
回答问题,并举例说明。
①无理数
+
有理数是什么数?
②无理数
-
有理数是什么数?
③无理数
×
有理数是什么数?
④无理数
÷
有理数是什么数?
⑤无理数
+
无理数是什么数?
⑥无理数
-
无理数是什么数?
⑦无理数
×
无理数是什么数?
⑧无理数
÷
无理数是什么数?
12.
一个正方形的边长为m,面积为5,求代数式的值。
13.
小明在地面上画了一条数轴,原点为O,用铁丝以O点为圆心,以单位长1为半径制作一个圆环,再拉直圆环,变成一条线段,最后从O点起以此线段截得点A,则A点表示哪一个数?
14.
设面积为的圆半径为.
①是有理数吗?请说明理由。
②请估计的整数部分是几?
③将保留到千分位是几?
15.
如图,把16个边长为1的正方形拼在一起,试解决下列问题:
①连接A到D,C,D的线段,哪几条是无理数?
②是什么三角形,为什么?
〖鲁教版五四制七年级上数学当堂达标〗
4.1无理数
4.【答案】:C
【解析】:π是无限不循环小数,除以3还是无限不循环小数,故是无限不循环小数,不是分数
故选C
5.【答案】:C
【解析】:
面积是16的正方形的边长是4,是有理数
两直角边分别为7和24的直角三角形的边长是25,是有理数
C.
-0.1123583145……(第3个数为前两个数的和,若和为两位数,则仅取个位数)是无理数
D.,是有理数
故选C
6.【答案】:B
【解析】:
试题分析:因为2<<3,所以,3<+1<4,选B
考点:实数的估算
二、填空题
7.【答案】:见解析
【解析】:
①
②
8.【答案】:见解析
【解析】:无理数分为三类:①有一定结构的无限小数,如0.102100210002……②特定意义的数,如π及含π的数③带根号并且开方开不尽的数,如
9.【答案】:见解析
【解析】:有理数总可以用
有限小数
或
无限循环小数表示,反过来
有限小数或
无限循环小数
也都是有理数;无理数总是
无限不循环小数
,反过来
无限不循环小数总是无理数
10.【答案】:13
【解析】:,,,,0,,,,,1.313311331113……其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=
,,1.313311331113……是无理数,所以x=3
,0,是整数,所以y=3
,,,0,,,1.313311331113……是非负数,所以z=7
所以x+y+z=13
三、解答题
11.【答案】:见解析
【解析】:①无理数
+
有理数是无理数,如
②无理数
-
有理数是无理数数,如
③无理数
×
有理数是无理数,如
④无理数
÷
有理数是无理数,如
⑤无理数
+
无理数可能是无理数,如,无理数
+
无理数也可能是有理数,如
⑥无理数
-
无理数可能是无理数,如,无理数
-
无理数也可能是有理数,如
⑦无理数
×
无理数可能是无理数,如
⑧无理数
÷
无理数是什么数?
12.【答案】:-4
【解析】:
∵一个正方形的边长为m,面积为5
∴,
∴
【答案】:
2π或-2π
【解析】:
∵以单位长1为半径制作一个圆环
∴圆环的周长=2π
∴OA=2π,
∵点A的位置如图所示
∴A点表示2π或-2π
14.【答案】:见解析
【解析】:
①∵面积为的圆半径为
∴
∵
∴
∵若是分数,则也是分数,所以不可能是分数
∴所以不可能是有理数
②
③∵
∴=2.4……
∵
∴=2.44……
∵
∴=2.449……
=2.449或2.450
