湖南省长沙市望城一中2016-2017学年高二(上)第一次调研数学试卷(理科)(解析版)
文档属性
| 名称 | 湖南省长沙市望城一中2016-2017学年高二(上)第一次调研数学试卷(理科)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-13 00:00:00 | ||
图片预览




文档简介
2016-2017学年湖南省长沙市望城一中高二(上)第一次调研数学试卷(理科)
一、选择题:本大题共12小题,每小题5分,共60分﹒在每小题给出的四个选项中,只有一项是符合题目要求的﹒
1.命题“ x>0,x2+x>0”的否定是( )
A. x0>0,x02+x0>0
B. x0>0,x02+x0≤0
C. x>0,x2+x≤0
D. x≤0,x2+x>0
2.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
3.若命题“p或q”为真,“非p”为真,则( )
A.p真q真
B.p假q真
C.p真q假
D.p假q假
4.2x2﹣5x﹣3<0的一个必要不充分条件是( )
A.﹣<x<3
B.﹣<x<0
C.﹣3<x<
D.﹣1<x<6
5.下列有关命题的说法错误的是( )
A.命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.若p∧q为假命题,则p、q均为假命题
D.对于命题p: x∈R,使得x2+x+1<0.则¬p: x∈R,均有x2+x+1≥0
6.双曲线=1的渐近线方程是( )
A.y=±x
B.y=±x
C.y=±x
D.y=±x
7.(文科做)椭圆2x2+3y2=1的焦点坐标( )
A.(0,)
B.(0,±1)
C.(±1,0)
D.(,0)
8.若焦点在x轴上的椭圆+=1的离心率是,则m等于( )
A.
B.
C.
D.
9.一动圆与两圆x2+y2=1和x2+y2﹣8x+12=0都外切,则动圆圆心轨迹为( )
A.圆
B.椭圆
C.双曲线的一支
D.抛物线
10.已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2]
B.(1,2)
C.[2,+∞)
D.(2,+∞)
11.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|=( )
A.10
B.9
C.8
D.6
12.在平面直角坐标系xOy中.已知向量、,||=||=1,
=0,点Q满足=(+),曲线C={P|=cosθ+sinθ,0≤θ≤2π},区域Ω={P|0<r≤||≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
A.1<r<R<3
B.1<r<3≤R
C.r≤1<R<3
D.1<r<3<R
二、填空题:本大题共4小题,每小题5分,共20分﹒
13.抛物线x2+12y=0的准线方程是 .
14.存在实数x,使得x2﹣4bx+3b<0成立,则b的取值范围是 .
15.椭圆+=1(a为定值,且a>)的左焦点为F,直线x=m与椭圆交于点A,B,△FAB的周长的最大值是12,则该椭圆的离心率是 .
16.对于曲线C:
=1,给出下面四个命题:
①由线C不可能表示椭圆;
②当1<k<4时,曲线C表示椭圆;
③若曲线C表示双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<
其中所有正确命题的序号为 .
三、解答题:本大题共6小题,共70分﹒解答应写出文字说明、证明过程或演算步骤﹒
17.分别求出下列曲线的方程:
(1)椭圆的两个焦点的坐标分别是(﹣4,0),(4,0),椭圆上任意一点P到两焦点的距离之和等于10,求椭圆的标准方程.
(2)双曲线C经过点(2,2),且与﹣x2=1具有相同的渐近线,求双曲线C的标准方程.
18.已知命题p:(x+1)(x﹣5)≤0,命题q:1﹣m≤x<1+m(m>0).
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“p∨q”为真命题,“p∧q”为假命题,求实数x的取值范围.
19.已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为,求b,c.
20.已知椭圆4x2+y2=1及直线y=x+m.
(1)当直线与椭圆有公共点时,求实数m的取值范围.
(2)求被椭圆截得的最长弦所在直线方程.
21.已知点A(0,﹣2),B(0,4),动点P(x,y)满足;
(1)求动点P的轨迹方程;
(2)设(1)中所求轨迹方程与直线y=x+2交于C、D两点;求证OC⊥OD(O为坐标原点).
22.已知双曲线E:﹣=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
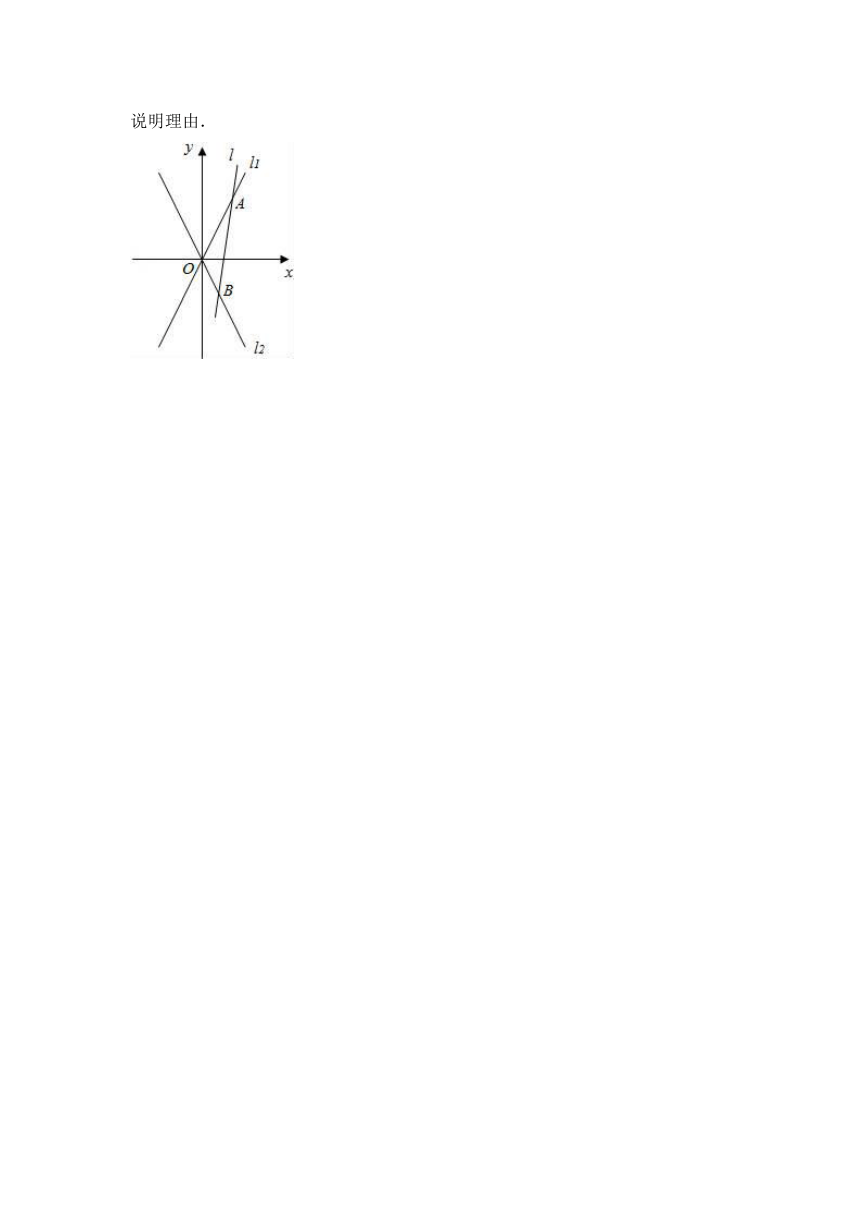
(2)如图,O点为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
2016-2017学年湖南省长沙市望城一中高二(上)第一次调研数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分﹒在每小题给出的四个选项中,只有一项是符合题目要求的﹒
1.命题“ x>0,x2+x>0”的否定是( )
A. x0>0,x02+x0>0
B. x0>0,x02+x0≤0
C. x>0,x2+x≤0
D. x≤0,x2+x>0
【考点】命题的否定.
【分析】直接利用全称命题的否定是特称命题写出结果即可.
【解答】解:因为全称命题的否定是特称命题,
所以命题“ x>0,x2+x>0”的否定为: x0>0,x02+x0≤0.
故选:B.
2.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】先根据mn>0看能否得出方程mx2+ny2=1的曲线是椭圆;这里可以利用举出特值的方法来验证,再看方程mx2+ny2=1的曲线是椭圆,根据椭圆的方程的定义,可以得出mn>0,即可得到结论.
【解答】解:当mn>0时,方程mx2+ny2=1的曲线不一定是椭圆,
例如:当m=n=1时,方程mx2+ny2=1的曲线不是椭圆而是圆;或者是m,n都是负数,曲线表示的也不是椭圆;
故前者不是后者的充分条件;
当方程mx2+ny2=1的曲线是椭圆时,应有m,n都大于0,且两个量不相等,得到mn>0;
由上可得:“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的必要不充分条件.
故选B.
3.若命题“p或q”为真,“非p”为真,则( )
A.p真q真
B.p假q真
C.p真q假
D.p假q假
【考点】复合命题的真假.
【分析】根据“非p”为真,得到p假,根据命题“p或q”为真,则p真或q真,从而得到答案.
【解答】解:若命题“p或q”为真,则p真或q真,
若“非p”为真,则p为假,
∴p假q真,
故选:B.
4.2x2﹣5x﹣3<0的一个必要不充分条件是( )
A.﹣<x<3
B.﹣<x<0
C.﹣3<x<
D.﹣1<x<6
【考点】必要条件、充分条件与充要条件的判断;一元二次不等式的解法.
【分析】通过解二次不等式求出2x2﹣5x﹣3<0的充要条件,通过对四个选项的范围与充要条件的范围间的包含关系的判断,得到2x2﹣5x﹣3<0的一个必要不充分条件.
【解答】解:2x2﹣5x﹣3<0的充要条件为
对于A是2x2﹣5x﹣3<0的充要条件
对于B,是2x2﹣5x﹣3<0的充分不必要条件
对于C,2x2﹣5x﹣3<0的不充分不必要条件
对于D,是2x2﹣5x﹣3<0的一个必要不充分条件
故选D
5.下列有关命题的说法错误的是( )
A.命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.若p∧q为假命题,则p、q均为假命题
D.对于命题p: x∈R,使得x2+x+1<0.则¬p: x∈R,均有x2+x+1≥0
【考点】命题的真假判断与应用;四种命题间的逆否关系;必要条件、充分条件与充要条件的判断.
【分析】根据四种命题的定义,我们可以判断A的真假;根据充要条件的定义,我们可以判断B的真假;根据复合命题的真值表,我们可以判断C的真假;根据特称命题的否定方法,我们可以判断D的真假,进而得到答案.
【解答】解:命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”故A为真命题;
“x=1”是“x2﹣3x+2=0”的充分不必要条件.故B为真命题;
若p∧q为假命题,则p、q存在至少一个假命题,但p、q不一定均为假命题,故C为假命题;
命题p: x∈R,使得x2+x+1<0.则非p: x∈R,均有x2+x+1≥0,故D为真命题;
故选C.
6.双曲线=1的渐近线方程是( )
A.y=±x
B.y=±x
C.y=±x
D.y=±x
【考点】双曲线的简单性质.
【分析】由双曲线的方程,得到a=5且b=2,利用双曲线渐近线方程的公式加以计算,可得答案.
【解答】解:由于双曲线,
则a=5且b=2,双曲线的渐近线方程为y=±x,
即y=x.
故选:A.
7.(文科做)椭圆2x2+3y2=1的焦点坐标( )
A.(0,)
B.(0,±1)
C.(±1,0)
D.(,0)
【考点】椭圆的简单性质.
【分析】先把椭圆方程化为标准方程,再确定其几何量,从而求出椭圆的焦点坐标.
【解答】解:椭圆方程化为标准方程为:
∵
∴椭圆的焦点在x轴上,且
∴
∴
故椭圆2x2+3y2=1的焦点坐标为
故选D.
8.若焦点在x轴上的椭圆+=1的离心率是,则m等于( )
A.
B.
C.
D.
【考点】椭圆的简单性质.
【分析】先根据椭圆的标准方程求得a,b,c,再结合椭圆的离心率公式列出关于m的方程,解之即得答案.
【解答】解:由题意,则
,
化简后得m=1.5,
故选A
9.一动圆与两圆x2+y2=1和x2+y2﹣8x+12=0都外切,则动圆圆心轨迹为( )
A.圆
B.椭圆
C.双曲线的一支
D.抛物线
【考点】双曲线的定义.
【分析】设动圆P的半径为r,然后根据⊙P与⊙O:x2+y2=1,⊙F:x2+y2﹣8x+12=0都外切得|PF|=2+r、|PO|=1+r,再两式相减消去参数r,则满足双曲线的定义,问题解决.
【解答】解:设动圆的圆心为P,半径为r,
而圆x2+y2=1的圆心为O(0,0),半径为1;
圆x2+y2﹣8x+12=0的圆心为F(4,0),半径为2.
依题意得|PF|=2+r|,|PO|=1+r,
则|PF|﹣|PO|=(2+r)﹣(1+r)=1<|FO|,
所以点P的轨迹是双曲线的一支.
故选C.
10.已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2]
B.(1,2)
C.[2,+∞)
D.(2,+∞)
【考点】双曲线的简单性质.
【分析】若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率.根据这个结论可以求出双曲线离心率的取值范围.
【解答】解:已知双曲线的右焦点为F,
若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,
则该直线的斜率的绝对值小于等于渐近线的斜率,
∴≥,离心率e2=,
∴e≥2,故选C
11.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|=( )
A.10
B.9
C.8
D.6
【考点】抛物线的简单性质.
【分析】抛物线
y2=4x
的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点,故|AB|=x1+x2+2,由此易得弦长值.
【解答】解:由题意,p=2,故抛物线的准线方程是x=﹣1,
∵抛物线
y2=4x
的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点
∴|AB|=x1+x2+2,
又x1+x2=6
∴∴|AB|=x1+x2+2=8
故选C.
12.在平面直角坐标系xOy中.已知向量、,||=||=1,
=0,点Q满足=(+),曲线C={P|=cosθ+sinθ,0≤θ≤2π},区域Ω={P|0<r≤||≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
A.1<r<R<3
B.1<r<3≤R
C.r≤1<R<3
D.1<r<3<R
【考点】向量在几何中的应用.
【分析】不妨令=(1,0),=(0,1),则P点的轨迹为单位圆,Ω={P|(0<r≤||≤R,r<R}表示的平面区域为:以Q点为圆心,内径为r,外径为R的圆环,若C∩Ω为两段分离的曲线,则单位圆与圆环的内外圆均相交,进而根据圆圆相交的充要条件得到答案.
【解答】解:∵平面直角坐标系xOy中.已知向量、,||=||=1,
=0,
不妨令=(1,0),=(0,1),
则=(+)=(,),
=cosθ+sinθ=(cosθ,sinθ),
故P点的轨迹为单位圆,
Ω={P|(0<r≤||≤R,r<R}表示的平面区域为:
以Q点为圆心,内径为r,外径为R的圆环,
若C∩Ω为两段分离的曲线,
则单位圆与圆环的内外圆均相交,
故|OQ|﹣1<r<R<|OQ|+1,
∵|OQ|=2,
故1<r<R<3,
故选:A
二、填空题:本大题共4小题,每小题5分,共20分﹒
13.抛物线x2+12y=0的准线方程是 y=3 .
【考点】抛物线的简单性质.
【分析】抛物线x2+12y=0化为x2=﹣12y,即可得到抛物线的准线方程.
【解答】解:抛物线x2+12y=0可化为x2=﹣12y,则2p=12,∴=3
∴抛物线x2+12y=0的准线方程是y=3
故答案为:y=3.
14.存在实数x,使得x2﹣4bx+3b<0成立,则b的取值范围是 b>或b<0 .
【考点】函数恒成立问题.
【分析】先把原命题等价转化为存在实数x,使得函数y=x2﹣4bx+3b的图象在X轴下方,再利用开口向上的二次函数图象的特点,转化为函数与X轴有两个交点,对应判别式大于0即可解题.
【解答】解:因为命题:存在实数x,使得x2﹣4bx+3b<0成立的等价说法是:
存在实数x,使得函数y=x2﹣4bx+3b的图象在X轴下方,
即函数与X轴有两个交点,故对应的△=(﹣4b)2﹣4×3b>0 b<0或b>.
故答案为:b<0或b>.
15.椭圆+=1(a为定值,且a>)的左焦点为F,直线x=m与椭圆交于点A,B,△FAB的周长的最大值是12,则该椭圆的离心率是 .
【考点】椭圆的简单性质.
【分析】先画出图象,结合图象以及椭圆的定义求出△FAB的周长的表达式,进而求出何时周长最大,即可求出椭圆的离心率.
【解答】解:设椭圆的右焦点E.如图:
由椭圆的定义得:△FAB的周长为:AB+AF+BF=AB+(2a﹣AE)+(2a﹣BE)=4a+AB﹣AE﹣BE;
∵AE+BE≥AB;
∴AB﹣AE﹣BE≤0,当AB过点E时取等号;
∴△FAB的周长:AB+AF+BF=4a+AB﹣AE﹣BE≤4a;
∴△FAB的周长的最大值是4a=12 a=3;
∴e===.
故答案:.
16.对于曲线C:
=1,给出下面四个命题:
①由线C不可能表示椭圆;
②当1<k<4时,曲线C表示椭圆;
③若曲线C表示双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<
其中所有正确命题的序号为 ③④ .
【考点】椭圆的标准方程;双曲线的标准方程.
【分析】据椭圆方程的特点列出不等式求出k的范围判断出①②错,据双曲线方程的特点列出不等式求出k的范围,判断出③对;据椭圆方程的特点列出不等式求出t的范围,判断出④错.
【解答】解:若C为椭圆应该满足即1<k<4
且k≠故①②错
若C为双曲线应该满足(4﹣k)(k﹣1)<0即k>4或k<1
故③对
若C表示椭圆,且长轴在x轴上应该满足4﹣k>k﹣1>0则
1<k<,故④对
故答案为:③④.
三、解答题:本大题共6小题,共70分﹒解答应写出文字说明、证明过程或演算步骤﹒
17.分别求出下列曲线的方程:
(1)椭圆的两个焦点的坐标分别是(﹣4,0),(4,0),椭圆上任意一点P到两焦点的距离之和等于10,求椭圆的标准方程.
(2)双曲线C经过点(2,2),且与﹣x2=1具有相同的渐近线,求双曲线C的标准方程.
【考点】椭圆的简单性质.
【分析】(1)由题意可知:设椭圆的方程:(a>b>0),则c=4,由椭圆的定义可知:2a=10,a=5,b2=a2﹣c2=9,即可求得椭圆的标准方程;
(2)设与﹣x2=1具有相同的渐近线的方程为﹣x2=λ,(λ≠0),将(2,2),代入椭圆方程即可求得λ=﹣4,即可求得双曲线C的标准方程.
【解答】解:(1)由椭圆的焦点在x轴上,设椭圆的方程:(a>b>0),
椭圆的两个焦点的坐标分别是(﹣4,0),(4,0),则c=4,
由椭圆的定义可知:2a=10,a=5,
b2=a2﹣c2=9,
∴椭圆的标准方程为:;
(2)设与﹣x2=1具有相同的渐近线的方程为﹣x2=λ,(λ≠0)
由双曲线C经过点(2,2),代入可知:λ=﹣4,
∴双曲线C的标准方程,
双曲线C的标准方程.
18.已知命题p:(x+1)(x﹣5)≤0,命题q:1﹣m≤x<1+m(m>0).
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“p∨q”为真命题,“p∧q”为假命题,求实数x的取值范围.
【考点】复合命题的真假.
【分析】(1)由于p是q的充分条件,可得[﹣1,5] [1﹣m,1+m),解出即可;
(2)由于“p∨q”为真命题,“p∧q”为假命题,可得命题p,q为一真一假.即可即可.
【解答】解:(1)由命题p:(x+1)(x﹣5)≤0,化为﹣1≤x≤5.
命题q:1﹣m≤x<1+m(m>0).
∵p是q的充分条件,
∴[﹣1,5] [1﹣m,1+m),
∴,解得m>4.
则实数m的取值范围为(4,+∞).
(2)∵m=5,∴命题q:﹣4≤x<6.
∵“p∨q”为真命题,“p∧q”为假命题,
∴命题p,q为一真一假.
当p真q假时,可得,解得x∈ .
当q真p假时,可得,解得﹣4≤x<﹣1或5<x<6.
因此x的取值范围是[﹣4,﹣1)∪(5,6).
19.已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为,求b,c.
【考点】解三角形.
【分析】(1)由正弦定理有:
sinAsinC﹣sinCcosA﹣sinC=0,可以求出A;
(2)有三角形面积以及余弦定理,可以求出b、c.
【解答】解:(1)c=asinC﹣ccosA,由正弦定理有:
sinAsinC﹣sinCcosA﹣sinC=0,即sinC (sinA﹣cosA﹣1)=0,
又,sinC≠0,
所以sinA﹣cosA﹣1=0,即2sin(A﹣)=1,
所以A=;
(2)S△ABC=bcsinA=,所以bc=4,
a=2,由余弦定理得:a2=b2+c2﹣2bccosA,即4=b2+c2﹣bc,
即有,
解得b=c=2.
20.已知椭圆4x2+y2=1及直线y=x+m.
(1)当直线与椭圆有公共点时,求实数m的取值范围.
(2)求被椭圆截得的最长弦所在直线方程.
【考点】直线与圆锥曲线的关系.
【分析】(1)当直线与椭圆有公共点时,直线方程与椭圆方程构成的方程组有解,等价于消掉y后得到x的二次方程有解,故△≥0,解出即可;
(2)设所截弦的两端点为A(x1,y1),B(x2,y2),由(1)及韦达定理可把弦长|AB|表示为关于m的函数,根据函数表达式易求弦长最大时m的值;
【解答】解:(1)由得5x2+2mx+m2﹣1=0,
当直线与椭圆有公共点时,△=4m2﹣4×5(m2﹣1)≥0,即﹣4m2+5≥0,
解得﹣,
所以实数m的取值范围是﹣;
(2)设所截弦的两端点为A(x1,y1),B(x2,y2),
由(1)知,,,
所以弦长|AB|=== =,
当m=0时|AB|最大,此时所求直线方程为y=x.
21.已知点A(0,﹣2),B(0,4),动点P(x,y)满足;
(1)求动点P的轨迹方程;
(2)设(1)中所求轨迹方程与直线y=x+2交于C、D两点;求证OC⊥OD(O为坐标原点).
【考点】直线与圆锥曲线的关系;轨迹方程.
【分析】(1)由,,代入可求
(2)联立,设C(x1,y1),D(x2,y2),则根据方程的根与系数关系可求x1+x2,x1x2,由y1y2=(x1+2)(x2+2)=x1x2+2(x1+x2)+4,代入到=x1x2+y1y2可证OC⊥OD
【解答】解:(1)∵A(0,﹣2),B(0,4),P(x,y)
∴,
∵
∴﹣x(﹣x)+(4﹣y)(﹣2﹣y)=y2﹣8
整理可得,x2=2y
(2)联立可得x2﹣2x﹣4=0
设C(x1,y1),D(x2,y2),则x1+x2=2,x1x2=﹣4,
∴y1y2=(x1+2)(x2+2)=x1x2+2(x1+x2)+4=4
∵=x1x2+y1y2=0
∴OC⊥OD
22.已知双曲线E:﹣=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O点为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
【考点】直线与圆锥曲线的综合问题.
【分析】(1)依题意,可知=2,易知c=a,从而可求双曲线E的离心率;
(2)由(1)知,双曲线E的方程为﹣=1,设直线l与x轴相交于点C,分l⊥x轴与直线l不与x轴垂直讨论,当l⊥x轴时,易求双曲线E的方程为﹣=1.当直线l不与x轴垂直时,设直线l的方程为y=kx+m,与双曲线E的方程联立,利用由S△OAB=|OC| |y1﹣y2|=8可证得:双曲线E的方程为﹣=1,从而可得答案.
【解答】解:(1)因为双曲线E的渐近线分别为l1:y=2x,l2:y=﹣2x,
所以=2.
所以=2.
故c=a,
从而双曲线E的离心率e==.
(2)由(1)知,双曲线E的方程为﹣=1.
设直线l与x轴相交于点C,
当l⊥x轴时,若直线l与双曲线E有且只有一个公共点,则|OC|=a,|AB|=4a,
所以|OC| |AB|=8,
因此a 4a=8,解得a=2,此时双曲线E的方程为﹣=1.
以下证明:当直线l不与x轴垂直时,双曲线E的方程为﹣=1也满足条件.
设直线l的方程为y=kx+m,依题意,得k>2或k<﹣2;
则C(﹣,0),记A(x1,y1),B(x2,y2),
由得y1=,同理得y2=,
由S△OAB=|OC| |y1﹣y2|得:
|﹣| |﹣|=8,即m2=4|4﹣k2|=4(k2﹣4).
由得:(4﹣k2)x2﹣2kmx﹣m2﹣16=0,
因为4﹣k2<0,
所以△=4k2m2+4(4﹣k2)(m2+16)=﹣16(4k2﹣m2﹣16),
又因为m2=4(k2﹣4),
所以△=0,即直线l与双曲线E有且只有一个公共点.
因此,存在总与直线l有且只有一个公共点的双曲线E,且E的方程为﹣=1.
2017年2月13日
一、选择题:本大题共12小题,每小题5分,共60分﹒在每小题给出的四个选项中,只有一项是符合题目要求的﹒
1.命题“ x>0,x2+x>0”的否定是( )
A. x0>0,x02+x0>0
B. x0>0,x02+x0≤0
C. x>0,x2+x≤0
D. x≤0,x2+x>0
2.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
3.若命题“p或q”为真,“非p”为真,则( )
A.p真q真
B.p假q真
C.p真q假
D.p假q假
4.2x2﹣5x﹣3<0的一个必要不充分条件是( )
A.﹣<x<3
B.﹣<x<0
C.﹣3<x<
D.﹣1<x<6
5.下列有关命题的说法错误的是( )
A.命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.若p∧q为假命题,则p、q均为假命题
D.对于命题p: x∈R,使得x2+x+1<0.则¬p: x∈R,均有x2+x+1≥0
6.双曲线=1的渐近线方程是( )
A.y=±x
B.y=±x
C.y=±x
D.y=±x
7.(文科做)椭圆2x2+3y2=1的焦点坐标( )
A.(0,)
B.(0,±1)
C.(±1,0)
D.(,0)
8.若焦点在x轴上的椭圆+=1的离心率是,则m等于( )
A.
B.
C.
D.
9.一动圆与两圆x2+y2=1和x2+y2﹣8x+12=0都外切,则动圆圆心轨迹为( )
A.圆
B.椭圆
C.双曲线的一支
D.抛物线
10.已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2]
B.(1,2)
C.[2,+∞)
D.(2,+∞)
11.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|=( )
A.10
B.9
C.8
D.6
12.在平面直角坐标系xOy中.已知向量、,||=||=1,
=0,点Q满足=(+),曲线C={P|=cosθ+sinθ,0≤θ≤2π},区域Ω={P|0<r≤||≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
A.1<r<R<3
B.1<r<3≤R
C.r≤1<R<3
D.1<r<3<R
二、填空题:本大题共4小题,每小题5分,共20分﹒
13.抛物线x2+12y=0的准线方程是 .
14.存在实数x,使得x2﹣4bx+3b<0成立,则b的取值范围是 .
15.椭圆+=1(a为定值,且a>)的左焦点为F,直线x=m与椭圆交于点A,B,△FAB的周长的最大值是12,则该椭圆的离心率是 .
16.对于曲线C:
=1,给出下面四个命题:
①由线C不可能表示椭圆;
②当1<k<4时,曲线C表示椭圆;
③若曲线C表示双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<
其中所有正确命题的序号为 .
三、解答题:本大题共6小题,共70分﹒解答应写出文字说明、证明过程或演算步骤﹒
17.分别求出下列曲线的方程:
(1)椭圆的两个焦点的坐标分别是(﹣4,0),(4,0),椭圆上任意一点P到两焦点的距离之和等于10,求椭圆的标准方程.
(2)双曲线C经过点(2,2),且与﹣x2=1具有相同的渐近线,求双曲线C的标准方程.
18.已知命题p:(x+1)(x﹣5)≤0,命题q:1﹣m≤x<1+m(m>0).
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“p∨q”为真命题,“p∧q”为假命题,求实数x的取值范围.
19.已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为,求b,c.
20.已知椭圆4x2+y2=1及直线y=x+m.
(1)当直线与椭圆有公共点时,求实数m的取值范围.
(2)求被椭圆截得的最长弦所在直线方程.
21.已知点A(0,﹣2),B(0,4),动点P(x,y)满足;
(1)求动点P的轨迹方程;
(2)设(1)中所求轨迹方程与直线y=x+2交于C、D两点;求证OC⊥OD(O为坐标原点).
22.已知双曲线E:﹣=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O点为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
2016-2017学年湖南省长沙市望城一中高二(上)第一次调研数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分﹒在每小题给出的四个选项中,只有一项是符合题目要求的﹒
1.命题“ x>0,x2+x>0”的否定是( )
A. x0>0,x02+x0>0
B. x0>0,x02+x0≤0
C. x>0,x2+x≤0
D. x≤0,x2+x>0
【考点】命题的否定.
【分析】直接利用全称命题的否定是特称命题写出结果即可.
【解答】解:因为全称命题的否定是特称命题,
所以命题“ x>0,x2+x>0”的否定为: x0>0,x02+x0≤0.
故选:B.
2.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】先根据mn>0看能否得出方程mx2+ny2=1的曲线是椭圆;这里可以利用举出特值的方法来验证,再看方程mx2+ny2=1的曲线是椭圆,根据椭圆的方程的定义,可以得出mn>0,即可得到结论.
【解答】解:当mn>0时,方程mx2+ny2=1的曲线不一定是椭圆,
例如:当m=n=1时,方程mx2+ny2=1的曲线不是椭圆而是圆;或者是m,n都是负数,曲线表示的也不是椭圆;
故前者不是后者的充分条件;
当方程mx2+ny2=1的曲线是椭圆时,应有m,n都大于0,且两个量不相等,得到mn>0;
由上可得:“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的必要不充分条件.
故选B.
3.若命题“p或q”为真,“非p”为真,则( )
A.p真q真
B.p假q真
C.p真q假
D.p假q假
【考点】复合命题的真假.
【分析】根据“非p”为真,得到p假,根据命题“p或q”为真,则p真或q真,从而得到答案.
【解答】解:若命题“p或q”为真,则p真或q真,
若“非p”为真,则p为假,
∴p假q真,
故选:B.
4.2x2﹣5x﹣3<0的一个必要不充分条件是( )
A.﹣<x<3
B.﹣<x<0
C.﹣3<x<
D.﹣1<x<6
【考点】必要条件、充分条件与充要条件的判断;一元二次不等式的解法.
【分析】通过解二次不等式求出2x2﹣5x﹣3<0的充要条件,通过对四个选项的范围与充要条件的范围间的包含关系的判断,得到2x2﹣5x﹣3<0的一个必要不充分条件.
【解答】解:2x2﹣5x﹣3<0的充要条件为
对于A是2x2﹣5x﹣3<0的充要条件
对于B,是2x2﹣5x﹣3<0的充分不必要条件
对于C,2x2﹣5x﹣3<0的不充分不必要条件
对于D,是2x2﹣5x﹣3<0的一个必要不充分条件
故选D
5.下列有关命题的说法错误的是( )
A.命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.若p∧q为假命题,则p、q均为假命题
D.对于命题p: x∈R,使得x2+x+1<0.则¬p: x∈R,均有x2+x+1≥0
【考点】命题的真假判断与应用;四种命题间的逆否关系;必要条件、充分条件与充要条件的判断.
【分析】根据四种命题的定义,我们可以判断A的真假;根据充要条件的定义,我们可以判断B的真假;根据复合命题的真值表,我们可以判断C的真假;根据特称命题的否定方法,我们可以判断D的真假,进而得到答案.
【解答】解:命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”故A为真命题;
“x=1”是“x2﹣3x+2=0”的充分不必要条件.故B为真命题;
若p∧q为假命题,则p、q存在至少一个假命题,但p、q不一定均为假命题,故C为假命题;
命题p: x∈R,使得x2+x+1<0.则非p: x∈R,均有x2+x+1≥0,故D为真命题;
故选C.
6.双曲线=1的渐近线方程是( )
A.y=±x
B.y=±x
C.y=±x
D.y=±x
【考点】双曲线的简单性质.
【分析】由双曲线的方程,得到a=5且b=2,利用双曲线渐近线方程的公式加以计算,可得答案.
【解答】解:由于双曲线,
则a=5且b=2,双曲线的渐近线方程为y=±x,
即y=x.
故选:A.
7.(文科做)椭圆2x2+3y2=1的焦点坐标( )
A.(0,)
B.(0,±1)
C.(±1,0)
D.(,0)
【考点】椭圆的简单性质.
【分析】先把椭圆方程化为标准方程,再确定其几何量,从而求出椭圆的焦点坐标.
【解答】解:椭圆方程化为标准方程为:
∵
∴椭圆的焦点在x轴上,且
∴
∴
故椭圆2x2+3y2=1的焦点坐标为
故选D.
8.若焦点在x轴上的椭圆+=1的离心率是,则m等于( )
A.
B.
C.
D.
【考点】椭圆的简单性质.
【分析】先根据椭圆的标准方程求得a,b,c,再结合椭圆的离心率公式列出关于m的方程,解之即得答案.
【解答】解:由题意,则
,
化简后得m=1.5,
故选A
9.一动圆与两圆x2+y2=1和x2+y2﹣8x+12=0都外切,则动圆圆心轨迹为( )
A.圆
B.椭圆
C.双曲线的一支
D.抛物线
【考点】双曲线的定义.
【分析】设动圆P的半径为r,然后根据⊙P与⊙O:x2+y2=1,⊙F:x2+y2﹣8x+12=0都外切得|PF|=2+r、|PO|=1+r,再两式相减消去参数r,则满足双曲线的定义,问题解决.
【解答】解:设动圆的圆心为P,半径为r,
而圆x2+y2=1的圆心为O(0,0),半径为1;
圆x2+y2﹣8x+12=0的圆心为F(4,0),半径为2.
依题意得|PF|=2+r|,|PO|=1+r,
则|PF|﹣|PO|=(2+r)﹣(1+r)=1<|FO|,
所以点P的轨迹是双曲线的一支.
故选C.
10.已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2]
B.(1,2)
C.[2,+∞)
D.(2,+∞)
【考点】双曲线的简单性质.
【分析】若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率.根据这个结论可以求出双曲线离心率的取值范围.
【解答】解:已知双曲线的右焦点为F,
若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,
则该直线的斜率的绝对值小于等于渐近线的斜率,
∴≥,离心率e2=,
∴e≥2,故选C
11.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|=( )
A.10
B.9
C.8
D.6
【考点】抛物线的简单性质.
【分析】抛物线
y2=4x
的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点,故|AB|=x1+x2+2,由此易得弦长值.
【解答】解:由题意,p=2,故抛物线的准线方程是x=﹣1,
∵抛物线
y2=4x
的焦点作直线交抛物线于A(x1,y1)B(x2,y2)两点
∴|AB|=x1+x2+2,
又x1+x2=6
∴∴|AB|=x1+x2+2=8
故选C.
12.在平面直角坐标系xOy中.已知向量、,||=||=1,
=0,点Q满足=(+),曲线C={P|=cosθ+sinθ,0≤θ≤2π},区域Ω={P|0<r≤||≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
A.1<r<R<3
B.1<r<3≤R
C.r≤1<R<3
D.1<r<3<R
【考点】向量在几何中的应用.
【分析】不妨令=(1,0),=(0,1),则P点的轨迹为单位圆,Ω={P|(0<r≤||≤R,r<R}表示的平面区域为:以Q点为圆心,内径为r,外径为R的圆环,若C∩Ω为两段分离的曲线,则单位圆与圆环的内外圆均相交,进而根据圆圆相交的充要条件得到答案.
【解答】解:∵平面直角坐标系xOy中.已知向量、,||=||=1,
=0,
不妨令=(1,0),=(0,1),
则=(+)=(,),
=cosθ+sinθ=(cosθ,sinθ),
故P点的轨迹为单位圆,
Ω={P|(0<r≤||≤R,r<R}表示的平面区域为:
以Q点为圆心,内径为r,外径为R的圆环,
若C∩Ω为两段分离的曲线,
则单位圆与圆环的内外圆均相交,
故|OQ|﹣1<r<R<|OQ|+1,
∵|OQ|=2,
故1<r<R<3,
故选:A
二、填空题:本大题共4小题,每小题5分,共20分﹒
13.抛物线x2+12y=0的准线方程是 y=3 .
【考点】抛物线的简单性质.
【分析】抛物线x2+12y=0化为x2=﹣12y,即可得到抛物线的准线方程.
【解答】解:抛物线x2+12y=0可化为x2=﹣12y,则2p=12,∴=3
∴抛物线x2+12y=0的准线方程是y=3
故答案为:y=3.
14.存在实数x,使得x2﹣4bx+3b<0成立,则b的取值范围是 b>或b<0 .
【考点】函数恒成立问题.
【分析】先把原命题等价转化为存在实数x,使得函数y=x2﹣4bx+3b的图象在X轴下方,再利用开口向上的二次函数图象的特点,转化为函数与X轴有两个交点,对应判别式大于0即可解题.
【解答】解:因为命题:存在实数x,使得x2﹣4bx+3b<0成立的等价说法是:
存在实数x,使得函数y=x2﹣4bx+3b的图象在X轴下方,
即函数与X轴有两个交点,故对应的△=(﹣4b)2﹣4×3b>0 b<0或b>.
故答案为:b<0或b>.
15.椭圆+=1(a为定值,且a>)的左焦点为F,直线x=m与椭圆交于点A,B,△FAB的周长的最大值是12,则该椭圆的离心率是 .
【考点】椭圆的简单性质.
【分析】先画出图象,结合图象以及椭圆的定义求出△FAB的周长的表达式,进而求出何时周长最大,即可求出椭圆的离心率.
【解答】解:设椭圆的右焦点E.如图:
由椭圆的定义得:△FAB的周长为:AB+AF+BF=AB+(2a﹣AE)+(2a﹣BE)=4a+AB﹣AE﹣BE;
∵AE+BE≥AB;
∴AB﹣AE﹣BE≤0,当AB过点E时取等号;
∴△FAB的周长:AB+AF+BF=4a+AB﹣AE﹣BE≤4a;
∴△FAB的周长的最大值是4a=12 a=3;
∴e===.
故答案:.
16.对于曲线C:
=1,给出下面四个命题:
①由线C不可能表示椭圆;
②当1<k<4时,曲线C表示椭圆;
③若曲线C表示双曲线,则k<1或k>4;
④若曲线C表示焦点在x轴上的椭圆,则1<k<
其中所有正确命题的序号为 ③④ .
【考点】椭圆的标准方程;双曲线的标准方程.
【分析】据椭圆方程的特点列出不等式求出k的范围判断出①②错,据双曲线方程的特点列出不等式求出k的范围,判断出③对;据椭圆方程的特点列出不等式求出t的范围,判断出④错.
【解答】解:若C为椭圆应该满足即1<k<4
且k≠故①②错
若C为双曲线应该满足(4﹣k)(k﹣1)<0即k>4或k<1
故③对
若C表示椭圆,且长轴在x轴上应该满足4﹣k>k﹣1>0则
1<k<,故④对
故答案为:③④.
三、解答题:本大题共6小题,共70分﹒解答应写出文字说明、证明过程或演算步骤﹒
17.分别求出下列曲线的方程:
(1)椭圆的两个焦点的坐标分别是(﹣4,0),(4,0),椭圆上任意一点P到两焦点的距离之和等于10,求椭圆的标准方程.
(2)双曲线C经过点(2,2),且与﹣x2=1具有相同的渐近线,求双曲线C的标准方程.
【考点】椭圆的简单性质.
【分析】(1)由题意可知:设椭圆的方程:(a>b>0),则c=4,由椭圆的定义可知:2a=10,a=5,b2=a2﹣c2=9,即可求得椭圆的标准方程;
(2)设与﹣x2=1具有相同的渐近线的方程为﹣x2=λ,(λ≠0),将(2,2),代入椭圆方程即可求得λ=﹣4,即可求得双曲线C的标准方程.
【解答】解:(1)由椭圆的焦点在x轴上,设椭圆的方程:(a>b>0),
椭圆的两个焦点的坐标分别是(﹣4,0),(4,0),则c=4,
由椭圆的定义可知:2a=10,a=5,
b2=a2﹣c2=9,
∴椭圆的标准方程为:;
(2)设与﹣x2=1具有相同的渐近线的方程为﹣x2=λ,(λ≠0)
由双曲线C经过点(2,2),代入可知:λ=﹣4,
∴双曲线C的标准方程,
双曲线C的标准方程.
18.已知命题p:(x+1)(x﹣5)≤0,命题q:1﹣m≤x<1+m(m>0).
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“p∨q”为真命题,“p∧q”为假命题,求实数x的取值范围.
【考点】复合命题的真假.
【分析】(1)由于p是q的充分条件,可得[﹣1,5] [1﹣m,1+m),解出即可;
(2)由于“p∨q”为真命题,“p∧q”为假命题,可得命题p,q为一真一假.即可即可.
【解答】解:(1)由命题p:(x+1)(x﹣5)≤0,化为﹣1≤x≤5.
命题q:1﹣m≤x<1+m(m>0).
∵p是q的充分条件,
∴[﹣1,5] [1﹣m,1+m),
∴,解得m>4.
则实数m的取值范围为(4,+∞).
(2)∵m=5,∴命题q:﹣4≤x<6.
∵“p∨q”为真命题,“p∧q”为假命题,
∴命题p,q为一真一假.
当p真q假时,可得,解得x∈ .
当q真p假时,可得,解得﹣4≤x<﹣1或5<x<6.
因此x的取值范围是[﹣4,﹣1)∪(5,6).
19.已知a,b,c分别为△ABC三个内角A,B,C的对边,c=asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为,求b,c.
【考点】解三角形.
【分析】(1)由正弦定理有:
sinAsinC﹣sinCcosA﹣sinC=0,可以求出A;
(2)有三角形面积以及余弦定理,可以求出b、c.
【解答】解:(1)c=asinC﹣ccosA,由正弦定理有:
sinAsinC﹣sinCcosA﹣sinC=0,即sinC (sinA﹣cosA﹣1)=0,
又,sinC≠0,
所以sinA﹣cosA﹣1=0,即2sin(A﹣)=1,
所以A=;
(2)S△ABC=bcsinA=,所以bc=4,
a=2,由余弦定理得:a2=b2+c2﹣2bccosA,即4=b2+c2﹣bc,
即有,
解得b=c=2.
20.已知椭圆4x2+y2=1及直线y=x+m.
(1)当直线与椭圆有公共点时,求实数m的取值范围.
(2)求被椭圆截得的最长弦所在直线方程.
【考点】直线与圆锥曲线的关系.
【分析】(1)当直线与椭圆有公共点时,直线方程与椭圆方程构成的方程组有解,等价于消掉y后得到x的二次方程有解,故△≥0,解出即可;
(2)设所截弦的两端点为A(x1,y1),B(x2,y2),由(1)及韦达定理可把弦长|AB|表示为关于m的函数,根据函数表达式易求弦长最大时m的值;
【解答】解:(1)由得5x2+2mx+m2﹣1=0,
当直线与椭圆有公共点时,△=4m2﹣4×5(m2﹣1)≥0,即﹣4m2+5≥0,
解得﹣,
所以实数m的取值范围是﹣;
(2)设所截弦的两端点为A(x1,y1),B(x2,y2),
由(1)知,,,
所以弦长|AB|=== =,
当m=0时|AB|最大,此时所求直线方程为y=x.
21.已知点A(0,﹣2),B(0,4),动点P(x,y)满足;
(1)求动点P的轨迹方程;
(2)设(1)中所求轨迹方程与直线y=x+2交于C、D两点;求证OC⊥OD(O为坐标原点).
【考点】直线与圆锥曲线的关系;轨迹方程.
【分析】(1)由,,代入可求
(2)联立,设C(x1,y1),D(x2,y2),则根据方程的根与系数关系可求x1+x2,x1x2,由y1y2=(x1+2)(x2+2)=x1x2+2(x1+x2)+4,代入到=x1x2+y1y2可证OC⊥OD
【解答】解:(1)∵A(0,﹣2),B(0,4),P(x,y)
∴,
∵
∴﹣x(﹣x)+(4﹣y)(﹣2﹣y)=y2﹣8
整理可得,x2=2y
(2)联立可得x2﹣2x﹣4=0
设C(x1,y1),D(x2,y2),则x1+x2=2,x1x2=﹣4,
∴y1y2=(x1+2)(x2+2)=x1x2+2(x1+x2)+4=4
∵=x1x2+y1y2=0
∴OC⊥OD
22.已知双曲线E:﹣=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O点为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
【考点】直线与圆锥曲线的综合问题.
【分析】(1)依题意,可知=2,易知c=a,从而可求双曲线E的离心率;
(2)由(1)知,双曲线E的方程为﹣=1,设直线l与x轴相交于点C,分l⊥x轴与直线l不与x轴垂直讨论,当l⊥x轴时,易求双曲线E的方程为﹣=1.当直线l不与x轴垂直时,设直线l的方程为y=kx+m,与双曲线E的方程联立,利用由S△OAB=|OC| |y1﹣y2|=8可证得:双曲线E的方程为﹣=1,从而可得答案.
【解答】解:(1)因为双曲线E的渐近线分别为l1:y=2x,l2:y=﹣2x,
所以=2.
所以=2.
故c=a,
从而双曲线E的离心率e==.
(2)由(1)知,双曲线E的方程为﹣=1.
设直线l与x轴相交于点C,
当l⊥x轴时,若直线l与双曲线E有且只有一个公共点,则|OC|=a,|AB|=4a,
所以|OC| |AB|=8,
因此a 4a=8,解得a=2,此时双曲线E的方程为﹣=1.
以下证明:当直线l不与x轴垂直时,双曲线E的方程为﹣=1也满足条件.
设直线l的方程为y=kx+m,依题意,得k>2或k<﹣2;
则C(﹣,0),记A(x1,y1),B(x2,y2),
由得y1=,同理得y2=,
由S△OAB=|OC| |y1﹣y2|得:
|﹣| |﹣|=8,即m2=4|4﹣k2|=4(k2﹣4).
由得:(4﹣k2)x2﹣2kmx﹣m2﹣16=0,
因为4﹣k2<0,
所以△=4k2m2+4(4﹣k2)(m2+16)=﹣16(4k2﹣m2﹣16),
又因为m2=4(k2﹣4),
所以△=0,即直线l与双曲线E有且只有一个公共点.
因此,存在总与直线l有且只有一个公共点的双曲线E,且E的方程为﹣=1.
2017年2月13日
同课章节目录
