第三章 图形的平移与旋转 单元测试卷
文档属性
| 名称 | 第三章 图形的平移与旋转 单元测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 620.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-13 13:08:27 | ||
图片预览


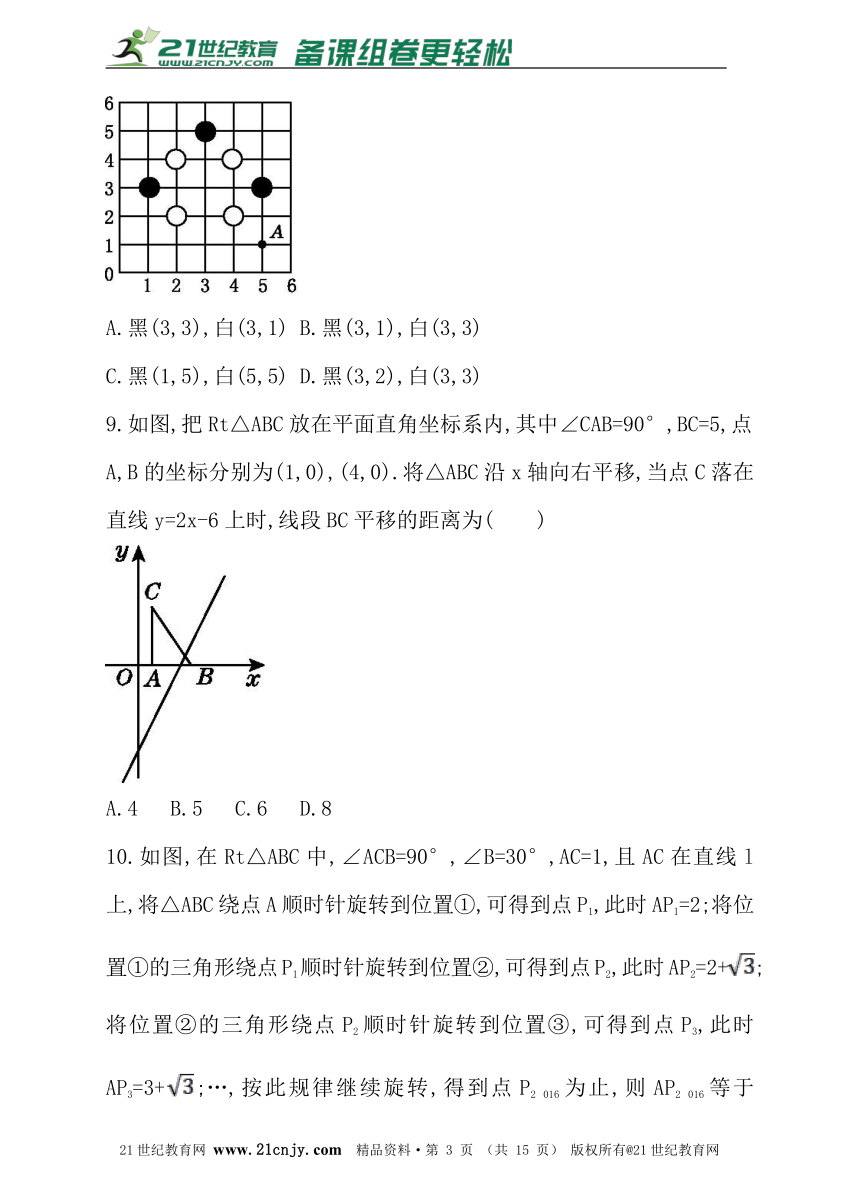
文档简介
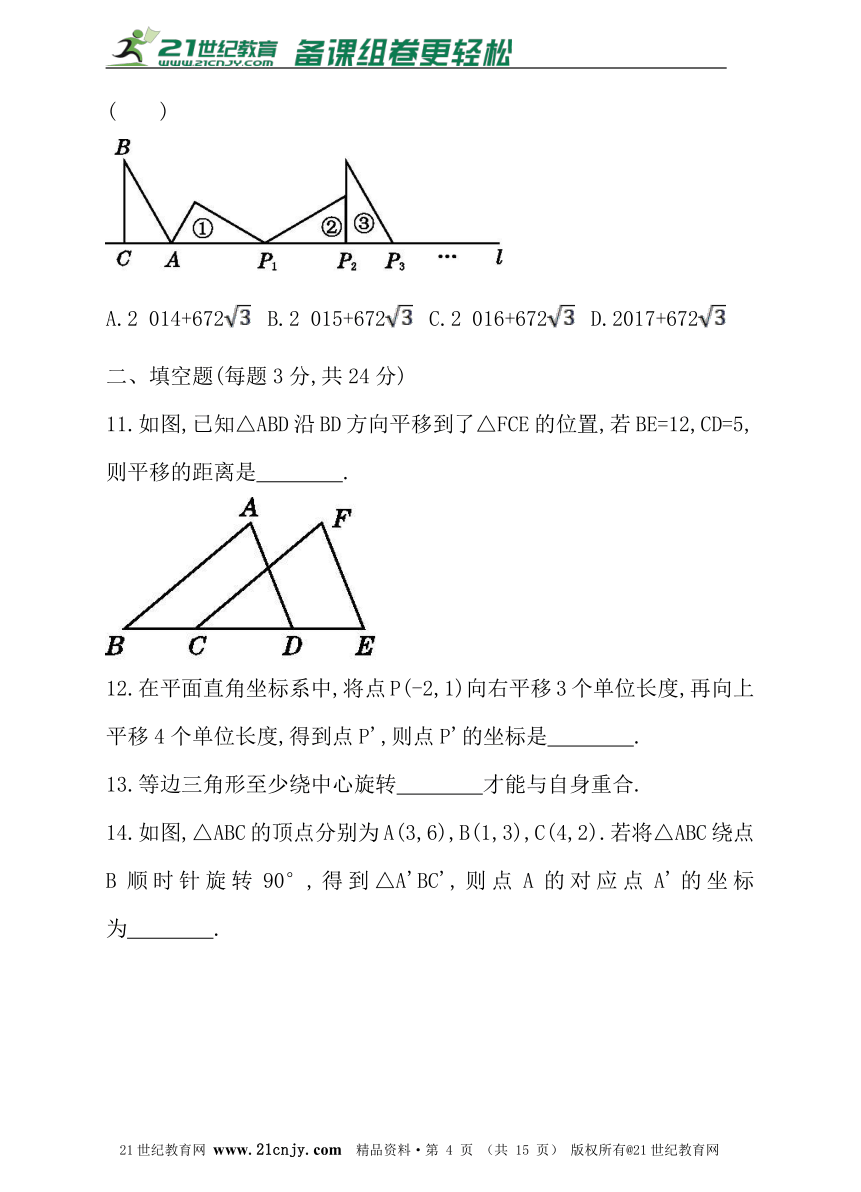
第三章 图形的平移与旋转 单元测试卷
一、选择题(每题3分,共30分)
1.下列各组图形中,可以通过平移变换由一个图形得到另一个图形的是( )
2.下面的图形是天气预报使用的图标,从左到右分别代表“霾”、“浮尘”、“扬沙”和“阴”,其中是中心对称图形的是( )
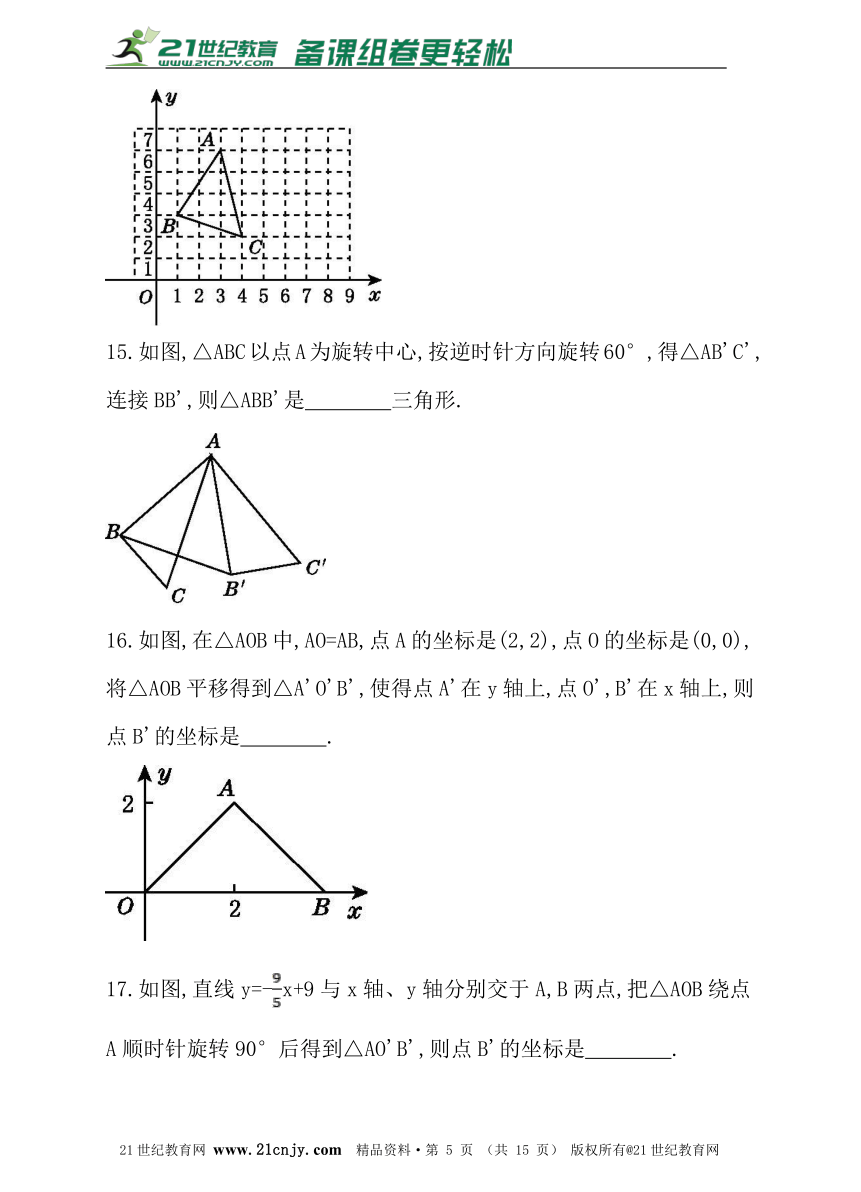
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.将点A(-2,-3)向右平移3个单位长度得到点B,则点B所处的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在Rt△ABO中,∠ABO=90°,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得△A'B'O,那么点A'的坐标为( )
A.(-,1) B.(-2,) C.(-1,) D.(-,2)
6.如果两个图形可通过旋转而相互得到,则下列说法中正确的个数是( )
①对应点连线的中垂线必经过旋转中心;②这两个图形的大小、形状相同;③对应线段一定相等且平行;
④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1 B.2 C.3 D.4
7.如图,∠AOB=80°,∠B=35°,将△AOB绕点O顺时针旋转,旋转角为α,得到△A'OB',若点A'在AB上,则旋转角α的大小是( )
A.40° B.50° C.75° D.90°
8.用棋子摆出的图案如图所示,棋子的位置用有序数对表示,如A点用(5,1)表示,如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A.黑(3,3),白(3,1) B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5) D.黑(3,2),白(3,3)
9.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC平移的距离为( )www.21-cn-jy.com
A.4 B.5 C.6 D.8
10.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+;…,按此规律继续旋转,得到点P2 016为止,则AP2 016等于( )【来源:21·世纪·教育·网】
A.2 014+672 B.2 015+672 C.2 016+672 D.2017+672
二、填空题(每题3分,共24分)
11.如图,已知△ABD沿BD方向平移到了△FCE的位置,若BE=12,CD=5,则平移的距离是 .21·世纪*教育网
12.在平面直角坐标系中,将点P(-2,1)向右平移3个单位长度,再向上平移4个单位长度,得到点P',则点P'的坐标是 .?
13.等边三角形至少绕中心旋转 才能与自身重合.?
14.如图,△ABC的顶点分别为A(3,6),B(1,3),C(4,2).若将△ABC绕点B顺时针旋转90°,得到△A'BC',则点A的对应点A'的坐标为 .2-1-c-n-j-y
15.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB'C',连接BB',则△ABB'是 三角形.【来源:21cnj*y.co*m】
16.如图,在△AOB中,AO=AB,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A'O'B',使得点A'在y轴上,点O',B'在x轴上,则点B'的坐标是 .【版权所有:21教育】
?
17.如图,直线y=-x+9与x轴、y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO'B',则点B'的坐标是 .
18.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后得到△AFB,连接EF,则有下列结论:①△AED≌△AEF;②BE+DC=DE;③S△ABE+S△ACD>S△AED;④BE2+DC2=DE2.其中正确的是 .(填入所有正确结论的序号)21教育名师原创作品
?
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.21*cnjy*com
20.如图,在直角三角形ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,△ABC沿AB方向平移至△DEF,若AE=8 cm,BD=2 cm.求:
(1)△ABC沿AB方向平移的距离;
(2)四边形AEFC的周长.
21.如图,△ABC和△DCE均是等边三角形,点B,C,E在同一直线上.连接AE,BD,AE交CD于点N,BD交AC于点M.2·1·c·n·j·y
(1)求证:△ACE≌△BCD.
(2)△BCM绕着点C顺时针旋转可得到哪个三角形?
(3)你还能找到两个可以通过旋转得到的三角形吗?若能,请你写出来.
22.实践与操作:现有如图①所示的两种瓷砖,请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼铺的图案是轴对称图形或中心对称图形(如图②所示).
(1)分别在图③、图④中各设计一种与图②不同的拼法,使其中的一个是轴对称图形而不是中心对称图形,另一个是中心对称图形而不是轴对称图形;【出处:21教育名师】
(2)分别在图⑤、图⑥中各设计一个拼铺图案,使这两个图案都既是轴对称图形又是中心对称图形,且互不相同(两个图案之间若能通过轴对称、平移、旋转变换相互得到,则视为相同图案).
23.如图①,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF,BE.
(1)线段AF和BE有怎样的数量关系?请说明理由.
(2)将图①中的△CEF绕点C旋转一定的角度,得到图②,(1)中的结论还成立吗?作出判断并说明理由.21*cnjy*com
24.如图,△ABC和△DEF为大小一样的等腰直角三角形,∠ACB=∠DFE=90°,AC=DF.将△DEF的顶点D置于△ABC的斜边AB的中点处,使△DEF绕点D沿顺时针方向旋转.
(1)当△DEF旋转到DF过直角顶点C时,如图①,DF与AC的交点H与点C重合,试判断∠DGB与∠DGH的关系,并说明理由.
(2)在(1)的条件下,将△DEF继续旋转,旋转角为α(0°<α<45°),如图②,(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
参考答案
一、1.【答案】A 2.【答案】A 3.【答案】A 4.【答案】D
5.【答案】C
解:在Rt△ABO中,∠ABO=90°,OA=2,AB=1,所以
OB=OB'=,A'B'=AB=1.因为点A'在第二象限,所以点A'的坐标为(-1,).故选C.
6.【答案】C
解:根据旋转的性质可知,对应点连线的中垂线必经过旋转中心,①正确;这两个图形的大小、形状相同,②正确;对应线段一定相等但不一定平行,所以③错误;将一个图形绕旋转中心旋转某个定角后必与另一个图形重合,④正确.故正确的说法有3个.故选C.
7.【答案】B
解:由旋转知,AO=A'O,在△AOB中,由∠AOB=80°,∠B=35°,得∠A=65°,所以∠AOA'=180°-2×65°=50°.
8.【答案】B
解:当摆放黑(3,3),白(3,1)时,组成的图案是轴对称图形但不是中心对称图形,故A项错误;当摆放黑(3,1),白(3,3)时,组成的图案是轴对称图形也是中心对称图形,故B项正确;当摆放黑(1,5),白(5,5)时,组成的图案既不是轴对称图形也不是中心对称图形,故C项错误;当摆放黑(3,2),白(3,3)时,组成的图案是轴对称图形不是中心对称图形,故D项错误.故选B.
9.【答案】A
解:∵点A,B的坐标分别为(1,0),(4,0),∴AB=3.∵∠CAB=90°,BC=5,∴AC=4.当点C落在直线y=2x-6上时,令2x-6=4,解得x=5,故线段BC平移的距离为5-1=4.
10.【答案】C
解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,∴AB=2.∴BC=.由题意知,AP1=2,AP2=2+,AP3=2++1=3+,每三次旋转为一个循环,又∵2 016÷3=672,∴AP2 016=672(3+)=2 016+672.故选C.
二、
11.【答案】3.5 12.【答案】(1,5) 13.【答案】120°
14.【答案】(4,1) 15.【答案】等边 16.【答案】(2,0)
17.【答案】(14,5)
解:易得A(5,0),B(0,9),旋转后点B'的纵坐标为5,横坐标为OA+O'B'=5+9=14,故点B'的坐标是(14,5).21教育网
18.【答案】①③④
解:由旋转知AF=AD,BF=CD,∠FBA=∠DCA,∠FAD=∠BAC=90°,∴∠FAE=∠EAD=45°.又AE=AE,∴△AED≌△AEF.∴DE=EF.∵∠EBF=∠FBA+∠ABE=∠ACD+∠ABE=90°,www-2-1-cnjy-com
∴、BE2+BF2=BE2+DC2=EF2=DE2.S△ABE+S△ACD=S△ABE+S△AFB>S△AED,BE+DC=BE+FB>EF=ED,∴正确的结论是①③④.
三、19.解:(1)如图所示.
(2)如图所示.
20.解:(1)∵△ABC沿AB方向平移至△DEF,
∴AD=BE.
∵AE=8 cm,DB=2 cm,
∴AD==3(cm),
即△ABC沿AB方向平移的距离是3 cm.
(2)由平移的特征及(1)得,
CF=AD=3 cm,EF=BC=3 cm.
又AE=8 cm,AC=4 cm,
∴四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
21.(1)证明:∵△ABC与△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°.
∴∠BCD=∠ACE.
∴△ACE≌△BCD.
(2)解:△BCM绕着点C顺时针旋转60°可得△ACN.
(3)解:能,△CMD绕着点C顺时针旋转60°可得到△CNE.△BCD绕着点C顺时针旋转60°可得到△ACE.21世纪教育网版权所有
22.解:(1)如图①是轴对称图形而不是中心对称图形.
如图②是中心对称图形而不是轴对称图形.
(2)如图③、图④、图⑤既是轴对称图形又是中心对称图形(画出其中的两个即可).
解:本题答案不唯一.
23.解:(1)AF=BE.
理由如下:∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACF=∠BCE=60°.即在△AFC与△BEC中,21cnjy.com
∴△AFC≌△BEC(SAS).
∴AF=BE.
(2)成立.
理由:∵△ABC和△CEF是等边三角形,
∴AC=BC,CF=CE,∠ACB=∠FCE=60°.∴∠ACB-∠FCB=∠FCE-∠FCB,即∠ACF=∠BCE.21·cn·jy·com
即在△AFC与△BEC中,
∴△AFC≌△BEC(SAS).
∴AF=BE.
24.解:(1)∠DGB=∠DGH.
理由如下:在等腰直角三角形ABC中,D是AB的中点,AC=BC,
∴∠BCD=∠ACD=45°.
又∵∠FDE=45°,∴∠CGD=90°.
∴∠DGB=∠DGH.
(2)(1)中的结论仍然成立,∠DGB=∠DGH.
证明:如图,连接DC,在BC上截取BI=CH,连接DI.易证DB=DC.
又∵∠DBI=∠DCH=45°,∴△DBI≌△DCH.
∴DI=DH,∠IDB=∠HDC.
∴∠HDI=∠CDB=90°.∴∠GDI=90°-∠FDE=45°=∠HDG.
又∵DG=DG,DH=DI,∴△DGH≌△DGI.∴∠DGB=∠DGH.
一、选择题(每题3分,共30分)
1.下列各组图形中,可以通过平移变换由一个图形得到另一个图形的是( )
2.下面的图形是天气预报使用的图标,从左到右分别代表“霾”、“浮尘”、“扬沙”和“阴”,其中是中心对称图形的是( )
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.将点A(-2,-3)向右平移3个单位长度得到点B,则点B所处的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在Rt△ABO中,∠ABO=90°,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°,得△A'B'O,那么点A'的坐标为( )
A.(-,1) B.(-2,) C.(-1,) D.(-,2)
6.如果两个图形可通过旋转而相互得到,则下列说法中正确的个数是( )
①对应点连线的中垂线必经过旋转中心;②这两个图形的大小、形状相同;③对应线段一定相等且平行;
④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合.
A.1 B.2 C.3 D.4
7.如图,∠AOB=80°,∠B=35°,将△AOB绕点O顺时针旋转,旋转角为α,得到△A'OB',若点A'在AB上,则旋转角α的大小是( )
A.40° B.50° C.75° D.90°
8.用棋子摆出的图案如图所示,棋子的位置用有序数对表示,如A点用(5,1)表示,如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A.黑(3,3),白(3,1) B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5) D.黑(3,2),白(3,3)
9.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC平移的距离为( )www.21-cn-jy.com
A.4 B.5 C.6 D.8
10.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+;…,按此规律继续旋转,得到点P2 016为止,则AP2 016等于( )【来源:21·世纪·教育·网】
A.2 014+672 B.2 015+672 C.2 016+672 D.2017+672
二、填空题(每题3分,共24分)
11.如图,已知△ABD沿BD方向平移到了△FCE的位置,若BE=12,CD=5,则平移的距离是 .21·世纪*教育网
12.在平面直角坐标系中,将点P(-2,1)向右平移3个单位长度,再向上平移4个单位长度,得到点P',则点P'的坐标是 .?
13.等边三角形至少绕中心旋转 才能与自身重合.?
14.如图,△ABC的顶点分别为A(3,6),B(1,3),C(4,2).若将△ABC绕点B顺时针旋转90°,得到△A'BC',则点A的对应点A'的坐标为 .2-1-c-n-j-y
15.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB'C',连接BB',则△ABB'是 三角形.【来源:21cnj*y.co*m】
16.如图,在△AOB中,AO=AB,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A'O'B',使得点A'在y轴上,点O',B'在x轴上,则点B'的坐标是 .【版权所有:21教育】
?
17.如图,直线y=-x+9与x轴、y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO'B',则点B'的坐标是 .
18.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后得到△AFB,连接EF,则有下列结论:①△AED≌△AEF;②BE+DC=DE;③S△ABE+S△ACD>S△AED;④BE2+DC2=DE2.其中正确的是 .(填入所有正确结论的序号)21教育名师原创作品
?
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.21*cnjy*com
20.如图,在直角三角形ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,△ABC沿AB方向平移至△DEF,若AE=8 cm,BD=2 cm.求:
(1)△ABC沿AB方向平移的距离;
(2)四边形AEFC的周长.
21.如图,△ABC和△DCE均是等边三角形,点B,C,E在同一直线上.连接AE,BD,AE交CD于点N,BD交AC于点M.2·1·c·n·j·y
(1)求证:△ACE≌△BCD.
(2)△BCM绕着点C顺时针旋转可得到哪个三角形?
(3)你还能找到两个可以通过旋转得到的三角形吗?若能,请你写出来.
22.实践与操作:现有如图①所示的两种瓷砖,请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼铺的图案是轴对称图形或中心对称图形(如图②所示).
(1)分别在图③、图④中各设计一种与图②不同的拼法,使其中的一个是轴对称图形而不是中心对称图形,另一个是中心对称图形而不是轴对称图形;【出处:21教育名师】
(2)分别在图⑤、图⑥中各设计一个拼铺图案,使这两个图案都既是轴对称图形又是中心对称图形,且互不相同(两个图案之间若能通过轴对称、平移、旋转变换相互得到,则视为相同图案).
23.如图①,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF,BE.
(1)线段AF和BE有怎样的数量关系?请说明理由.
(2)将图①中的△CEF绕点C旋转一定的角度,得到图②,(1)中的结论还成立吗?作出判断并说明理由.21*cnjy*com
24.如图,△ABC和△DEF为大小一样的等腰直角三角形,∠ACB=∠DFE=90°,AC=DF.将△DEF的顶点D置于△ABC的斜边AB的中点处,使△DEF绕点D沿顺时针方向旋转.
(1)当△DEF旋转到DF过直角顶点C时,如图①,DF与AC的交点H与点C重合,试判断∠DGB与∠DGH的关系,并说明理由.
(2)在(1)的条件下,将△DEF继续旋转,旋转角为α(0°<α<45°),如图②,(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
参考答案
一、1.【答案】A 2.【答案】A 3.【答案】A 4.【答案】D
5.【答案】C
解:在Rt△ABO中,∠ABO=90°,OA=2,AB=1,所以
OB=OB'=,A'B'=AB=1.因为点A'在第二象限,所以点A'的坐标为(-1,).故选C.
6.【答案】C
解:根据旋转的性质可知,对应点连线的中垂线必经过旋转中心,①正确;这两个图形的大小、形状相同,②正确;对应线段一定相等但不一定平行,所以③错误;将一个图形绕旋转中心旋转某个定角后必与另一个图形重合,④正确.故正确的说法有3个.故选C.
7.【答案】B
解:由旋转知,AO=A'O,在△AOB中,由∠AOB=80°,∠B=35°,得∠A=65°,所以∠AOA'=180°-2×65°=50°.
8.【答案】B
解:当摆放黑(3,3),白(3,1)时,组成的图案是轴对称图形但不是中心对称图形,故A项错误;当摆放黑(3,1),白(3,3)时,组成的图案是轴对称图形也是中心对称图形,故B项正确;当摆放黑(1,5),白(5,5)时,组成的图案既不是轴对称图形也不是中心对称图形,故C项错误;当摆放黑(3,2),白(3,3)时,组成的图案是轴对称图形不是中心对称图形,故D项错误.故选B.
9.【答案】A
解:∵点A,B的坐标分别为(1,0),(4,0),∴AB=3.∵∠CAB=90°,BC=5,∴AC=4.当点C落在直线y=2x-6上时,令2x-6=4,解得x=5,故线段BC平移的距离为5-1=4.
10.【答案】C
解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,∴AB=2.∴BC=.由题意知,AP1=2,AP2=2+,AP3=2++1=3+,每三次旋转为一个循环,又∵2 016÷3=672,∴AP2 016=672(3+)=2 016+672.故选C.
二、
11.【答案】3.5 12.【答案】(1,5) 13.【答案】120°
14.【答案】(4,1) 15.【答案】等边 16.【答案】(2,0)
17.【答案】(14,5)
解:易得A(5,0),B(0,9),旋转后点B'的纵坐标为5,横坐标为OA+O'B'=5+9=14,故点B'的坐标是(14,5).21教育网
18.【答案】①③④
解:由旋转知AF=AD,BF=CD,∠FBA=∠DCA,∠FAD=∠BAC=90°,∴∠FAE=∠EAD=45°.又AE=AE,∴△AED≌△AEF.∴DE=EF.∵∠EBF=∠FBA+∠ABE=∠ACD+∠ABE=90°,www-2-1-cnjy-com
∴、BE2+BF2=BE2+DC2=EF2=DE2.S△ABE+S△ACD=S△ABE+S△AFB>S△AED,BE+DC=BE+FB>EF=ED,∴正确的结论是①③④.
三、19.解:(1)如图所示.
(2)如图所示.
20.解:(1)∵△ABC沿AB方向平移至△DEF,
∴AD=BE.
∵AE=8 cm,DB=2 cm,
∴AD==3(cm),
即△ABC沿AB方向平移的距离是3 cm.
(2)由平移的特征及(1)得,
CF=AD=3 cm,EF=BC=3 cm.
又AE=8 cm,AC=4 cm,
∴四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
21.(1)证明:∵△ABC与△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°.
∴∠BCD=∠ACE.
∴△ACE≌△BCD.
(2)解:△BCM绕着点C顺时针旋转60°可得△ACN.
(3)解:能,△CMD绕着点C顺时针旋转60°可得到△CNE.△BCD绕着点C顺时针旋转60°可得到△ACE.21世纪教育网版权所有
22.解:(1)如图①是轴对称图形而不是中心对称图形.
如图②是中心对称图形而不是轴对称图形.
(2)如图③、图④、图⑤既是轴对称图形又是中心对称图形(画出其中的两个即可).
解:本题答案不唯一.
23.解:(1)AF=BE.
理由如下:∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACF=∠BCE=60°.即在△AFC与△BEC中,21cnjy.com
∴△AFC≌△BEC(SAS).
∴AF=BE.
(2)成立.
理由:∵△ABC和△CEF是等边三角形,
∴AC=BC,CF=CE,∠ACB=∠FCE=60°.∴∠ACB-∠FCB=∠FCE-∠FCB,即∠ACF=∠BCE.21·cn·jy·com
即在△AFC与△BEC中,
∴△AFC≌△BEC(SAS).
∴AF=BE.
24.解:(1)∠DGB=∠DGH.
理由如下:在等腰直角三角形ABC中,D是AB的中点,AC=BC,
∴∠BCD=∠ACD=45°.
又∵∠FDE=45°,∴∠CGD=90°.
∴∠DGB=∠DGH.
(2)(1)中的结论仍然成立,∠DGB=∠DGH.
证明:如图,连接DC,在BC上截取BI=CH,连接DI.易证DB=DC.
又∵∠DBI=∠DCH=45°,∴△DBI≌△DCH.
∴DI=DH,∠IDB=∠HDC.
∴∠HDI=∠CDB=90°.∴∠GDI=90°-∠FDE=45°=∠HDG.
又∵DG=DG,DH=DI,∴△DGH≌△DGI.∴∠DGB=∠DGH.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
