17.2 勾股定理的逆定理 第1课时同步练习
文档属性
| 名称 | 17.2 勾股定理的逆定理 第1课时同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 397.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:33:42 | ||
图片预览


文档简介
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
基础训练
知识点1逆命题、逆定理
1.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
2.已知下列命题:①若a>b,则ac>bc;②若a=1,则=a;③内错角相等.其中原命题与逆命题均为真命题的个数是( )21·cn·jy·com
A.0 B.1 C.2 D.3
3.下列定理中,没有逆定理的是( )
A.直角三角形的两锐角互余
B.若三角形三边长a,b,c(其中aC.全等三角形的对应角相等
D.互为相反数的两数之和为0
知识点2 勾股定理的逆定理
4.(2016·南京)下列长度的三条线段能组成直角三角形的是( )
A.3,4,4 B.3,4,5
C.3,4,6 D.3,4,7
5.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠B为直角
C.∠C为直角 D.△ABC不是直角三角形
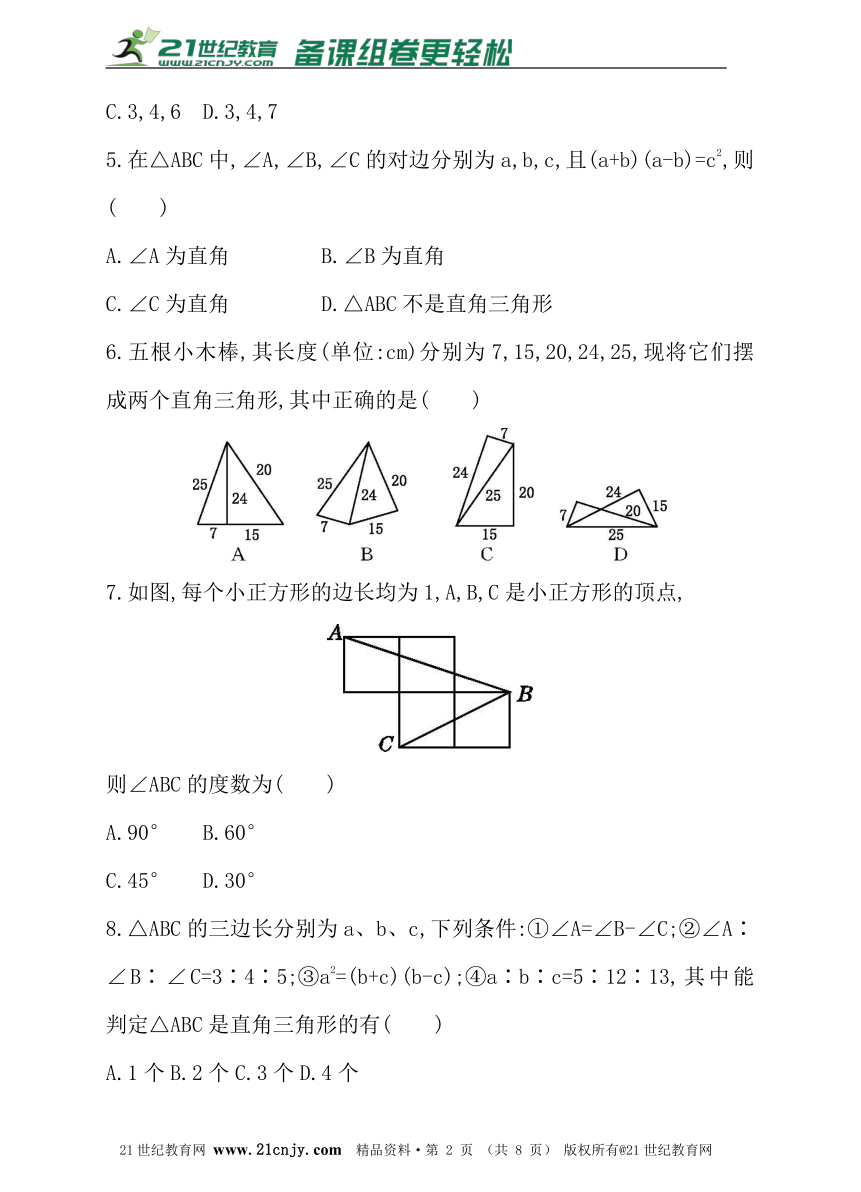
6.五根小木棒,其长度(单位:cm)分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )21·世纪*教育网
7.如图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,
则∠ABC的度数为( )
A.90° B.60°
C.45° D.30°
8.△ABC的三边长分别为a、b、c,下列条件:①∠A=∠B-∠C;②∠A∶∠B∶∠C=3∶4∶5;③a2=(b+c)(b-c);④a∶b∶c=5∶12∶13,其中能判定△ABC是直角三角形的有( )21*cnjy*com
A.1个 B.2个 C.3个 D.4个
知识点3 勾股数
9.下面几组数中,为勾股数的一组是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1
10.下列几组数:①9,12,15;②8,15,17;③7,24,25;④n2-1,2n,n2+1(n是大于1的整数),其中是勾股数的有( )www-2-1-cnjy-com
A.1组 B.2组 C.3组 D.4组
11.给出下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是一组勾股数;
②如果直角三角形的两边长分别是3和4,那么另一边长的平方必为25;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a是斜边长,那么a2∶b2∶c2=2∶1∶1.其中正确的是( )【来源:21cnj*y.co*m】
A.①② B.①③ C.①④ D.②④
易错点 忽视勾股数是正整数这一条件
12.下列各组数能构成勾股数的是 .(填序号)?
①6,8,10; ②7,8,10; ③,,1.
提升训练
考查角度1 利用三角形三边的数量关系求网格中三角形的面积和角度
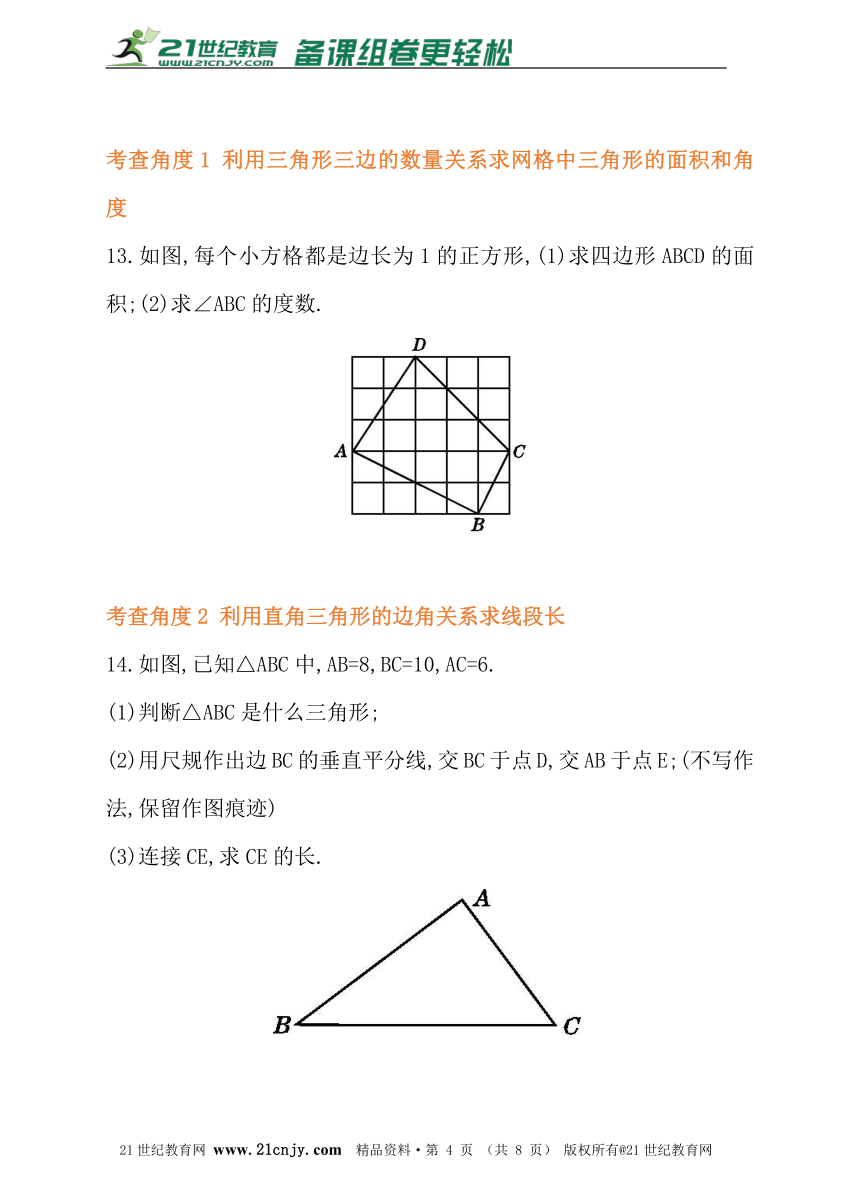
13.如图,每个小方格都是边长为1的正方形,(1)求四边形ABCD的面积;(2)求∠ABC的度数.
考查角度2 利用直角三角形的边角关系求线段长
14.如图,已知△ABC中,AB=8,BC=10,AC=6.
(1)判断△ABC是什么三角形;
(2)用尺规作出边BC的垂直平分线,交BC于点D,交AB于点E;(不写作法,保留作图痕迹)
(3)连接CE,求CE的长.
探究培优
拔尖角度1 利用勾股数的特征探究勾股数(从特殊到一般的思想)
15.观察下列勾股数:
①3,4,5,且32=4+5;
②5,12,13,且52=12+13;
③7,24,25,且72=24+25;
④9,b,c,且92=b+c;
…
(1)请你根据上述规律,并结合相关知识可得:
b= ,c= ;?
(2)猜想第n组勾股数(n为正整数),并证明你的猜想.
拔尖角度2 利用勾股定理的逆定理求角的度数(旋转法)
16.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数.21世纪教育网版权所有
参考答案
1.【答案】B
2.【答案】A
解:试题分析:①若a>b,则ac>bc是假命题,逆命题:若ac>bc,则a>b也是假命题;②若a=1,则=a是真命题,逆命题:若=a,则a=1是假命题;③内错角相等是假命题,逆命题:相等的角是内错角也是假命题;故选A.【来源:21·世纪·教育·网】
3.【答案】C 4.【答案】C
5.【答案】A
解:∵(a+b)(a-b)=c2,
∴a2-b2=c2,即c2+b2=a2,故此三角形是直角三角形,a为直角三角形的斜边,∴∠A为直角.故选A.2-1-c-n-j-y
6.【答案】C
7.【答案】C
解:连接AC,根据勾股定理可以得到AC2=BC2=5,
AB2=10.
即AC2+BC2=AB2,
所以△ABC是等腰直角三角形.
所以∠ABC=45°.故选C.
8.【答案】C
解:①中,∵∠A=∠B-∠C,∠A+∠B+∠C=180°,
∴∠B=90°,∴△ABC是直角三角形;②中,由∠A∶∠B∶∠C=3∶4∶5得△ABC中最大角∠C=180°×=75°,则△ABC为锐角三角形;③中,a2=(b+c)(b-c)=b2-c2,即a2+c2=b2,所以△ABC是直角三角形;④中,因为a∶b∶c=5∶12∶13,所以a2+b2=c2,故△ABC是直角三角形,故选C.www.21-cn-jy.com
9.【答案】B
解:A中虽然4,5,6均为正整数,但42+52≠62;C中虽然(-10)2+242=262,但-10<0;D中虽然满足2.42+4.52=5.12,但不是整数.2·1·c·n·j·y
方法总结:勾股数的特征:勾股数为三个正整数,且满足两个较小数的平方和等于最大数的平方.常见的勾股数
有:3,4,5;5,12,13;8,15,17;9,40,41.记住常见的勾股数可以提高做题速度.
10.【答案】D 11.【答案】C
12.【答案】①
易错总结:首先要注意到勾股数必须是一组正整数,其次要满足两个较小数的平方和等于最大数的平方.本题易误认为③也是勾股数.
13.解:(1)S四边形ABCD=S△ABC+S△ACD=×5×2+×5×3=.
(2)因为AB2=22+42=20,BC2=12+22=5,AC2=52=25,
所以AB2+BC2=AC2.
所以∠ABC=90°.
14.解:(1)因为AB=8,BC=10,AC=6,102=82+62,所以BC2=AB2+AC2,所以△ABC是直角三角形.21教育网
(2)如图所示.
(3)如图,设CE=x,因为DE垂直平分BC,所以BE=CE=x,在Rt△ACE中,可得:CE2=AE2+AC2,即:x2=(8-x)2+62,21cnjy.com
解得:x=6.25.
所以CE的长为6.25.
15.解:(1)40;41
(2)猜想第n组勾股数为2n+1,2n2+2n,2n2+2n+1.
证明如下:因为
(2n+1)2+(2n2+2n)2=4n4+8n3+8n2+4n+1,(2n2+2n+1)2=4n4+8n3+8n2+4n+1,
所以(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.
因为n是正整数,所以2n+1,2n2+2n,2n2+2n+1是一组勾股数.
16.解:如图,将△CPB绕点C顺时针旋转90°,得△CP'A,则
P'C=PC=2,P'A=PB=1,连接PP'.∵∠PCP'=90°,∴PP'2=22+22=8.又
P'A=1,PA=3,而PP'2+P'A2=8+1=9,PA2=9,∴PP'2+P'A2=PA2.
∴∠AP'P=90°,又∠CP'P=45°.
∴∠BPC=∠CP'A=135°.
第1课时 勾股定理的逆定理
基础训练
知识点1逆命题、逆定理
1.下列说法正确的是( )
A.每个定理都有逆定理
B.每个命题都有逆命题
C.原命题是假命题,则它的逆命题也是假命题
D.真命题的逆命题是真命题
2.已知下列命题:①若a>b,则ac>bc;②若a=1,则=a;③内错角相等.其中原命题与逆命题均为真命题的个数是( )21·cn·jy·com
A.0 B.1 C.2 D.3
3.下列定理中,没有逆定理的是( )
A.直角三角形的两锐角互余
B.若三角形三边长a,b,c(其中a
D.互为相反数的两数之和为0
知识点2 勾股定理的逆定理
4.(2016·南京)下列长度的三条线段能组成直角三角形的是( )
A.3,4,4 B.3,4,5
C.3,4,6 D.3,4,7
5.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠B为直角
C.∠C为直角 D.△ABC不是直角三角形
6.五根小木棒,其长度(单位:cm)分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )21·世纪*教育网
7.如图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,
则∠ABC的度数为( )
A.90° B.60°
C.45° D.30°
8.△ABC的三边长分别为a、b、c,下列条件:①∠A=∠B-∠C;②∠A∶∠B∶∠C=3∶4∶5;③a2=(b+c)(b-c);④a∶b∶c=5∶12∶13,其中能判定△ABC是直角三角形的有( )21*cnjy*com
A.1个 B.2个 C.3个 D.4个
知识点3 勾股数
9.下面几组数中,为勾股数的一组是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1
10.下列几组数:①9,12,15;②8,15,17;③7,24,25;④n2-1,2n,n2+1(n是大于1的整数),其中是勾股数的有( )www-2-1-cnjy-com
A.1组 B.2组 C.3组 D.4组
11.给出下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是一组勾股数;
②如果直角三角形的两边长分别是3和4,那么另一边长的平方必为25;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a是斜边长,那么a2∶b2∶c2=2∶1∶1.其中正确的是( )【来源:21cnj*y.co*m】
A.①② B.①③ C.①④ D.②④
易错点 忽视勾股数是正整数这一条件
12.下列各组数能构成勾股数的是 .(填序号)?
①6,8,10; ②7,8,10; ③,,1.
提升训练
考查角度1 利用三角形三边的数量关系求网格中三角形的面积和角度
13.如图,每个小方格都是边长为1的正方形,(1)求四边形ABCD的面积;(2)求∠ABC的度数.
考查角度2 利用直角三角形的边角关系求线段长
14.如图,已知△ABC中,AB=8,BC=10,AC=6.
(1)判断△ABC是什么三角形;
(2)用尺规作出边BC的垂直平分线,交BC于点D,交AB于点E;(不写作法,保留作图痕迹)
(3)连接CE,求CE的长.
探究培优
拔尖角度1 利用勾股数的特征探究勾股数(从特殊到一般的思想)
15.观察下列勾股数:
①3,4,5,且32=4+5;
②5,12,13,且52=12+13;
③7,24,25,且72=24+25;
④9,b,c,且92=b+c;
…
(1)请你根据上述规律,并结合相关知识可得:
b= ,c= ;?
(2)猜想第n组勾股数(n为正整数),并证明你的猜想.
拔尖角度2 利用勾股定理的逆定理求角的度数(旋转法)
16.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数.21世纪教育网版权所有
参考答案
1.【答案】B
2.【答案】A
解:试题分析:①若a>b,则ac>bc是假命题,逆命题:若ac>bc,则a>b也是假命题;②若a=1,则=a是真命题,逆命题:若=a,则a=1是假命题;③内错角相等是假命题,逆命题:相等的角是内错角也是假命题;故选A.【来源:21·世纪·教育·网】
3.【答案】C 4.【答案】C
5.【答案】A
解:∵(a+b)(a-b)=c2,
∴a2-b2=c2,即c2+b2=a2,故此三角形是直角三角形,a为直角三角形的斜边,∴∠A为直角.故选A.2-1-c-n-j-y
6.【答案】C
7.【答案】C
解:连接AC,根据勾股定理可以得到AC2=BC2=5,
AB2=10.
即AC2+BC2=AB2,
所以△ABC是等腰直角三角形.
所以∠ABC=45°.故选C.
8.【答案】C
解:①中,∵∠A=∠B-∠C,∠A+∠B+∠C=180°,
∴∠B=90°,∴△ABC是直角三角形;②中,由∠A∶∠B∶∠C=3∶4∶5得△ABC中最大角∠C=180°×=75°,则△ABC为锐角三角形;③中,a2=(b+c)(b-c)=b2-c2,即a2+c2=b2,所以△ABC是直角三角形;④中,因为a∶b∶c=5∶12∶13,所以a2+b2=c2,故△ABC是直角三角形,故选C.www.21-cn-jy.com
9.【答案】B
解:A中虽然4,5,6均为正整数,但42+52≠62;C中虽然(-10)2+242=262,但-10<0;D中虽然满足2.42+4.52=5.12,但不是整数.2·1·c·n·j·y
方法总结:勾股数的特征:勾股数为三个正整数,且满足两个较小数的平方和等于最大数的平方.常见的勾股数
有:3,4,5;5,12,13;8,15,17;9,40,41.记住常见的勾股数可以提高做题速度.
10.【答案】D 11.【答案】C
12.【答案】①
易错总结:首先要注意到勾股数必须是一组正整数,其次要满足两个较小数的平方和等于最大数的平方.本题易误认为③也是勾股数.
13.解:(1)S四边形ABCD=S△ABC+S△ACD=×5×2+×5×3=.
(2)因为AB2=22+42=20,BC2=12+22=5,AC2=52=25,
所以AB2+BC2=AC2.
所以∠ABC=90°.
14.解:(1)因为AB=8,BC=10,AC=6,102=82+62,所以BC2=AB2+AC2,所以△ABC是直角三角形.21教育网
(2)如图所示.
(3)如图,设CE=x,因为DE垂直平分BC,所以BE=CE=x,在Rt△ACE中,可得:CE2=AE2+AC2,即:x2=(8-x)2+62,21cnjy.com
解得:x=6.25.
所以CE的长为6.25.
15.解:(1)40;41
(2)猜想第n组勾股数为2n+1,2n2+2n,2n2+2n+1.
证明如下:因为
(2n+1)2+(2n2+2n)2=4n4+8n3+8n2+4n+1,(2n2+2n+1)2=4n4+8n3+8n2+4n+1,
所以(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.
因为n是正整数,所以2n+1,2n2+2n,2n2+2n+1是一组勾股数.
16.解:如图,将△CPB绕点C顺时针旋转90°,得△CP'A,则
P'C=PC=2,P'A=PB=1,连接PP'.∵∠PCP'=90°,∴PP'2=22+22=8.又
P'A=1,PA=3,而PP'2+P'A2=8+1=9,PA2=9,∴PP'2+P'A2=PA2.
∴∠AP'P=90°,又∠CP'P=45°.
∴∠BPC=∠CP'A=135°.
