18.1.1 平行四边形的对角线性质 同步练习
文档属性
| 名称 | 18.1.1 平行四边形的对角线性质 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 475.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:17:04 | ||
图片预览

文档简介
18.1 平行四边形
第2课时 平行四边形的对角线性质
基础训练
知识点1 平行四边形的性质——对角线互相平分
1.如图,?ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB
2.如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交
于点O,则OA的取值范围是( )
A.2 cmC.1 cm3.(2016·丽水)如图,?ABCD的对角线AC,BD交于点O,已知
AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13 B.17 C.20 D.26
4.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若
AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
5.如图,在?ABCD中,对角线AC与BD交于点O,AE⊥BD于E,CF⊥BD于F,则图中全等的三角形共有( )2·1·c·n·j·y
A.7对 B.6对
C.5对 D.4对
6.如图,?ABCD的对角线AC与BD相交于O,OE⊥BD于O交BC于E,连接DE,若△CED的周长是21 cm,则?ABCD的周长是 .?
知识点2 平行四边形的面积
7.将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )
A.1种 B.2种 C.4种 D.无数种
8.如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD的面积为( )
A.2 B. C. D.15
9.如图,过?ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的?AEMG的面积S1与?HCFM的面积S2的大小关系是( )【来源:21·世纪·教育·网】
A.S1>S2 B.S1C.S1=S2 D.2S1=S2
10.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )21·世纪*教育网
A.3 B.6 C.12 D.24
易错点 容易把未知条件当作已知条件使用
11.如图,在平行四边形ABCD中,AC和BD相交于点O,OE⊥AD于点E,OF⊥BC于点F.
试说明:OE=OF.
提升训练
考查角度1 利用平行四边形的对角线性质证明线段相等(构造法)
12.如图,已知?ABCD和?EBFD的顶点A,E,F,C在一条直线上,求证:AE=CF.
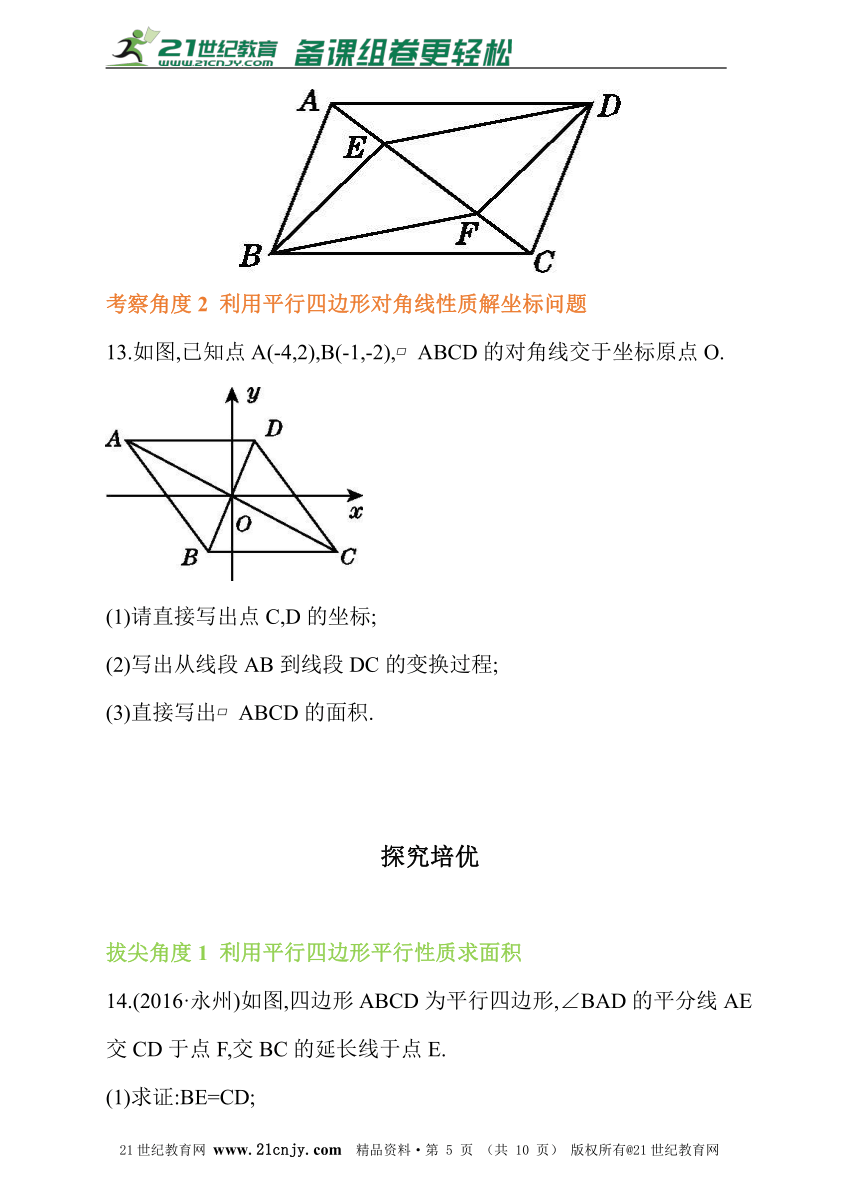
考察角度2 利用平行四边形对角线性质解坐标问题
13.如图,已知点A(-4,2),B(-1,-2),?ABCD的对角线交于坐标原点O.
(1)请直接写出点C,D的坐标;
(2)写出从线段AB到线段DC的变换过程;
(3)直接写出?ABCD的面积.
探究培优
拔尖角度1 利用平行四边形平行性质求面积
14.(2016·永州)如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E.21世纪教育网版权所有
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求?ABCD的面积.
拔尖角度2 利用平行四边形对角线性质探究面积
15.探究:如图①,?ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是否将?ABCD的面积分成二等份?试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.www.21-cn-jy.com
参考答案
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】C
解:在?ABCD中,OA=OC,OB=OD,所以AO=AC=3.在Rt△AOB中,根据勾股定理得OB===5,所以BD=2OB=2×5=10.
5.【答案】A
6.【答案】42 cm
7.【答案】D
解:此题易错选B,原因是只注意到对角线平分平行四边形的面积,而忽略任意一条过平行四边形对角线交点的直线都平分这个平行四边形的面积,实际上这样的折纸方法有无数种.21cnjy.com
8.【答案】C 9.【答案】C
10.【答案】C
解:本题运用了割补法,将分散的阴影部分通过割补转化为规则的几何阴影图形,从而求出面积.
11.错解:∵四边形ABCD为平行四边形,
∴OA=OC,∵OE⊥AD于点E,OF⊥BC于点F,
∴∠AEO=∠CFO=90°,
又∠AOE=∠COF,∴△AOE≌△COF,∴OE=OF.
诊断:错解误认为E,O,F三点共线,从而得到∠AOE=∠COF,而已知条件中并没有这个.E,O,F三点共线需要在解题过程中加以推理,否则就犯了逻辑错误.21·cn·jy·com
正解:∵四边形ABCD为平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
∴△AOE≌△COF,∴OE=OF.
12.证明:如图,连接BD交AC于O,
∵四边形ABCD和四边形EBFD都为平行四边形,∴OA=OC,OE=OF,
∴OA-OE=OC-OF,即AE=CF.
13.解:(1)C(4,-2),D(1,2).
(2)线段AB向右平移5个单位长度得到线段DC.
(3)S?ABCD=20.
14.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,BA=CD.
∴∠DAE=∠E.
又∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠BAE=∠E.
∴BA=BE,∴BE=CD.
(2)解:∵∠BEA=60°,BA=BE,
∴△ABE为等边三角形.
∵BF⊥AE,∴F为AE的中点,
∴AF=EF.
在△AFD和△EFC中,
∴△AFD≌△EFC(ASA).
∴△AFD的面积等于△EFC的面积.
∴?ABCD的面积等于△ABE的面积.
在Rt△ABF中,AB=4,AF=EF=2,∴BF=2.
∴△ABE的面积为×4×2=4.
∴?ABCD的面积为4.
15.探究:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC.
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF.∴AE=CF.同理可证△DOE≌△BOF,
∴DE=BF.又∵AB=DC,
∴AE+EF+BF+AB=CF+EF+DE+DC.
即四边形AEFB与四边形DEFC的周长相等.
(2)解:是.理由如下:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠OAB=∠OCD.
又∵∠AOB=∠COD,
∴△AOB≌△COD.
∴S△AOB=S△COD.由(1)知,△AOE≌△COF,△DOE≌△BOF,∴S△AOE=S△COF,S△DOE=S△BOF.∴S△AOE+S△AOB+S△BOF=S△COF+S△COD+S△DOE,即直线EF将?ABCD的面积分成二等份.21教育网
应用:连接AC,BD交于点O,作直线OP,则直线OP两旁的四边形面积相等.
第2课时 平行四边形的对角线性质
基础训练
知识点1 平行四边形的性质——对角线互相平分
1.如图,?ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB
2.如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交
于点O,则OA的取值范围是( )
A.2 cm
AD=8,BD=12,AC=6,则△OBC的周长为( )
A.13 B.17 C.20 D.26
4.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若
AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
5.如图,在?ABCD中,对角线AC与BD交于点O,AE⊥BD于E,CF⊥BD于F,则图中全等的三角形共有( )2·1·c·n·j·y
A.7对 B.6对
C.5对 D.4对
6.如图,?ABCD的对角线AC与BD相交于O,OE⊥BD于O交BC于E,连接DE,若△CED的周长是21 cm,则?ABCD的周长是 .?
知识点2 平行四边形的面积
7.将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )
A.1种 B.2种 C.4种 D.无数种
8.如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD的面积为( )
A.2 B. C. D.15
9.如图,过?ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的?AEMG的面积S1与?HCFM的面积S2的大小关系是( )【来源:21·世纪·教育·网】
A.S1>S2 B.S1
10.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )21·世纪*教育网
A.3 B.6 C.12 D.24
易错点 容易把未知条件当作已知条件使用
11.如图,在平行四边形ABCD中,AC和BD相交于点O,OE⊥AD于点E,OF⊥BC于点F.
试说明:OE=OF.
提升训练
考查角度1 利用平行四边形的对角线性质证明线段相等(构造法)
12.如图,已知?ABCD和?EBFD的顶点A,E,F,C在一条直线上,求证:AE=CF.
考察角度2 利用平行四边形对角线性质解坐标问题
13.如图,已知点A(-4,2),B(-1,-2),?ABCD的对角线交于坐标原点O.
(1)请直接写出点C,D的坐标;
(2)写出从线段AB到线段DC的变换过程;
(3)直接写出?ABCD的面积.
探究培优
拔尖角度1 利用平行四边形平行性质求面积
14.(2016·永州)如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E.21世纪教育网版权所有
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求?ABCD的面积.
拔尖角度2 利用平行四边形对角线性质探究面积
15.探究:如图①,?ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是否将?ABCD的面积分成二等份?试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.www.21-cn-jy.com
参考答案
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】C
解:在?ABCD中,OA=OC,OB=OD,所以AO=AC=3.在Rt△AOB中,根据勾股定理得OB===5,所以BD=2OB=2×5=10.
5.【答案】A
6.【答案】42 cm
7.【答案】D
解:此题易错选B,原因是只注意到对角线平分平行四边形的面积,而忽略任意一条过平行四边形对角线交点的直线都平分这个平行四边形的面积,实际上这样的折纸方法有无数种.21cnjy.com
8.【答案】C 9.【答案】C
10.【答案】C
解:本题运用了割补法,将分散的阴影部分通过割补转化为规则的几何阴影图形,从而求出面积.
11.错解:∵四边形ABCD为平行四边形,
∴OA=OC,∵OE⊥AD于点E,OF⊥BC于点F,
∴∠AEO=∠CFO=90°,
又∠AOE=∠COF,∴△AOE≌△COF,∴OE=OF.
诊断:错解误认为E,O,F三点共线,从而得到∠AOE=∠COF,而已知条件中并没有这个.E,O,F三点共线需要在解题过程中加以推理,否则就犯了逻辑错误.21·cn·jy·com
正解:∵四边形ABCD为平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
∴△AOE≌△COF,∴OE=OF.
12.证明:如图,连接BD交AC于O,
∵四边形ABCD和四边形EBFD都为平行四边形,∴OA=OC,OE=OF,
∴OA-OE=OC-OF,即AE=CF.
13.解:(1)C(4,-2),D(1,2).
(2)线段AB向右平移5个单位长度得到线段DC.
(3)S?ABCD=20.
14.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,BA=CD.
∴∠DAE=∠E.
又∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠BAE=∠E.
∴BA=BE,∴BE=CD.
(2)解:∵∠BEA=60°,BA=BE,
∴△ABE为等边三角形.
∵BF⊥AE,∴F为AE的中点,
∴AF=EF.
在△AFD和△EFC中,
∴△AFD≌△EFC(ASA).
∴△AFD的面积等于△EFC的面积.
∴?ABCD的面积等于△ABE的面积.
在Rt△ABF中,AB=4,AF=EF=2,∴BF=2.
∴△ABE的面积为×4×2=4.
∴?ABCD的面积为4.
15.探究:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC.
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF.∴AE=CF.同理可证△DOE≌△BOF,
∴DE=BF.又∵AB=DC,
∴AE+EF+BF+AB=CF+EF+DE+DC.
即四边形AEFB与四边形DEFC的周长相等.
(2)解:是.理由如下:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠OAB=∠OCD.
又∵∠AOB=∠COD,
∴△AOB≌△COD.
∴S△AOB=S△COD.由(1)知,△AOE≌△COF,△DOE≌△BOF,∴S△AOE=S△COF,S△DOE=S△BOF.∴S△AOE+S△AOB+S△BOF=S△COF+S△COD+S△DOE,即直线EF将?ABCD的面积分成二等份.21教育网
应用:连接AC,BD交于点O,作直线OP,则直线OP两旁的四边形面积相等.
