18.1.1平行四边形的边、角性质 同步练习
文档属性
| 名称 | 18.1.1平行四边形的边、角性质 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:15:20 | ||
图片预览


文档简介
18.1 平行四边形
第1课时 平行四边形的边、角性质
基础训练
知识点1 平行四边形的定义
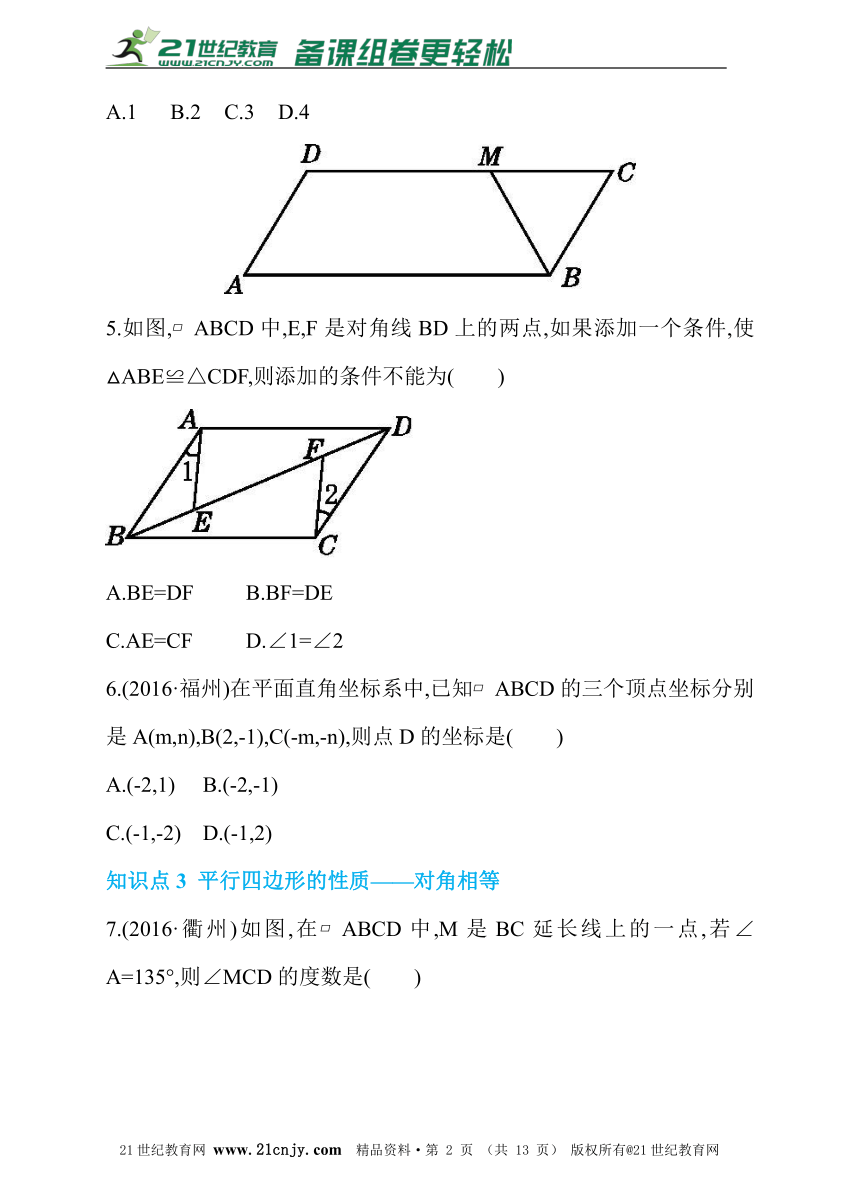
1.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,EF与HN相交于点O,则图中共有平行四边形( )2·1·c·n·j·y21世纪教育网版权所有
A.12个 B.9个 C.7个 D.5个
2.(2016·泰安)如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )21·世纪*教育网
A.2 B.3 C.4 D.6
知识点2 平行四边形的性质——对边相等
3.已知?ABCD的周长为32,AB=4,则BC等于( )
A.4 B.12 C.24 D.28
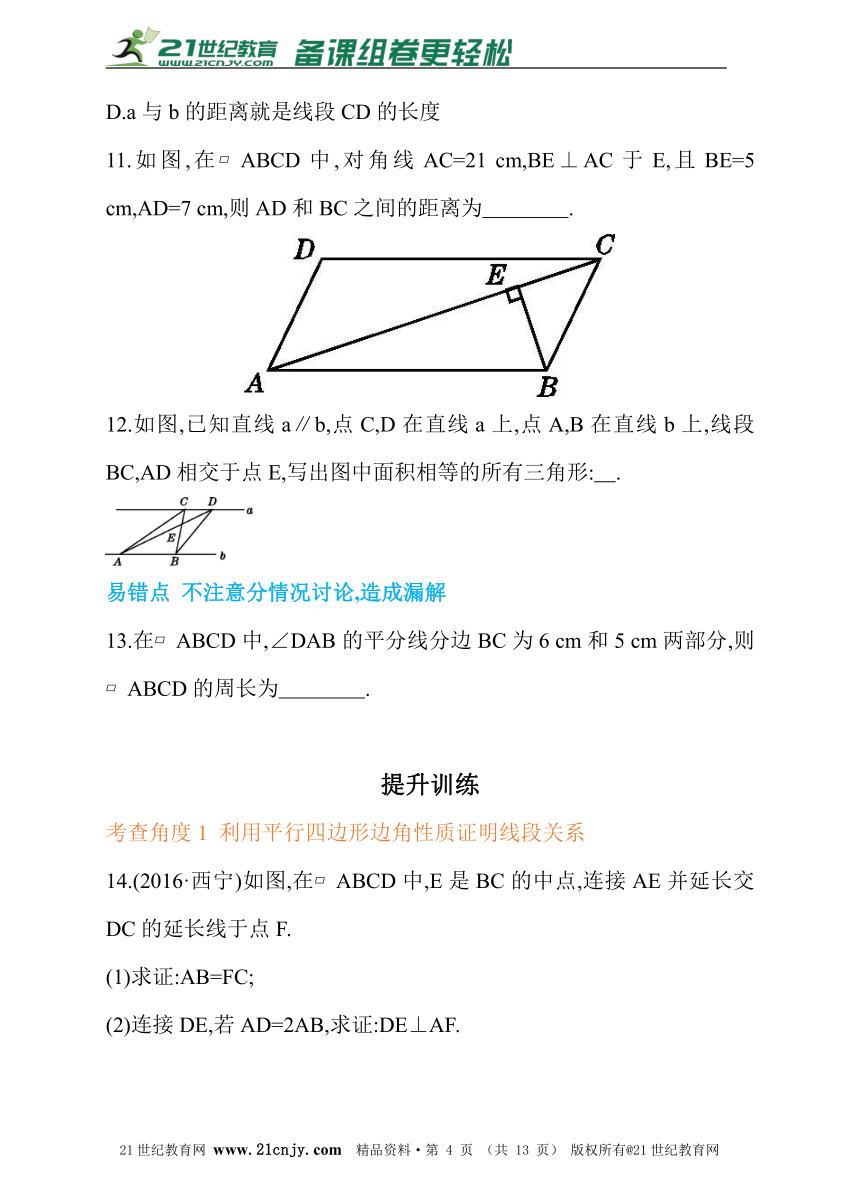
4.如图,在?ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )2-1-c-n-j-y21教育网
A.1 B.2 C.3 D.4
5.如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )21*cnjy*com【来源:21·世纪·教育·网】
A.BE=DF B.BF=DE
C.AE=CF D.∠1=∠2
6.(2016·福州)在平面直角坐标系中,已知?ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )【来源:21cnj*y.co*m】
A.(-2,1) B.(-2,-1)
C.(-1,-2) D.(-1,2)
知识点3 平行四边形的性质——对角相等
7.(2016·衢州)如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )21cnjy.comwww.21-cn-jy.com
A.45° B.55° C.65° D.75°
8.如图,在?ABCD中,CE⊥AB,E为垂足,如果∠A=120°,那么∠BCE的度数是( )
A.80° B.50° C.40° D.30°
9.已知?ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
知识点4 平行线之间的距离
10.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法不正确的是( )
A.AB=CD
B.EC=FG
C.A,B两点间的距离就是线段AB的长度
D.a与b的距离就是线段CD的长度
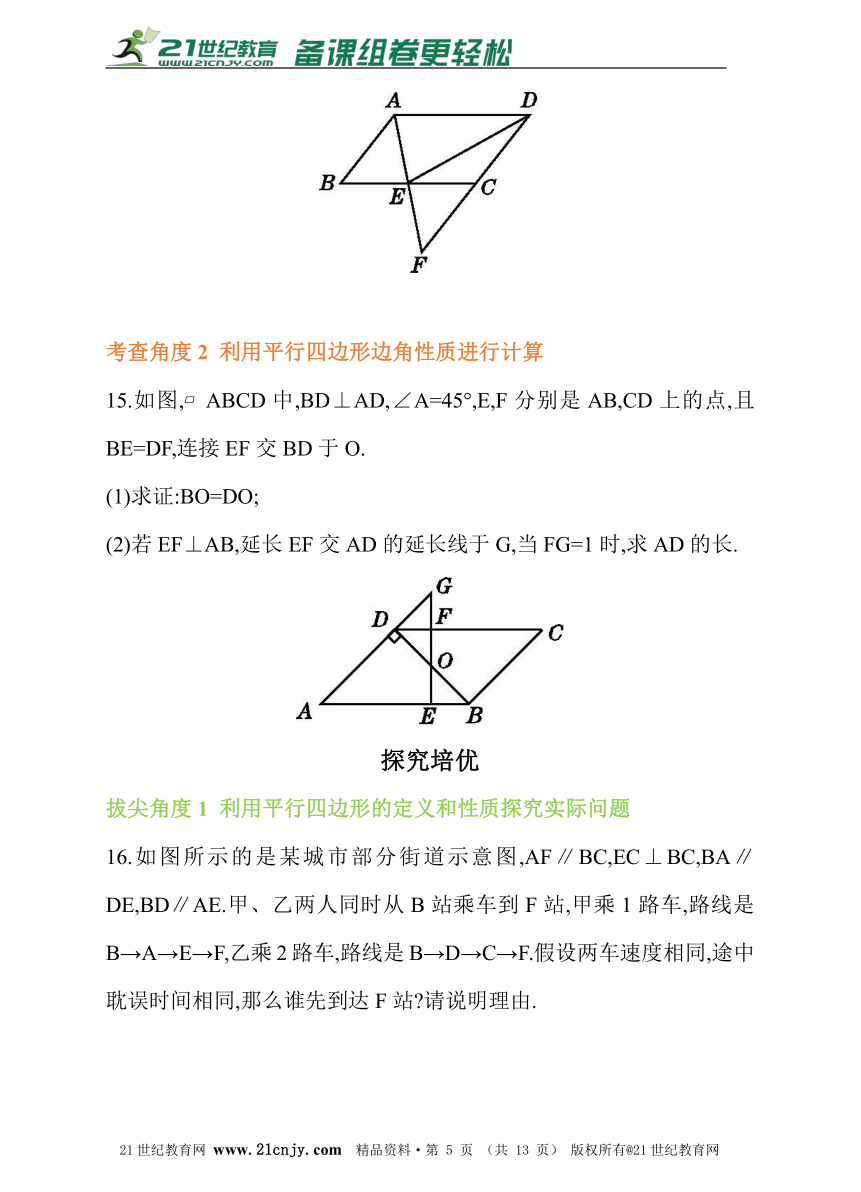
11.如图,在?ABCD中,对角线AC=21 cm,BE⊥AC于E,且BE=5 cm,AD=7 cm,则AD和BC之间的距离为 .?21世纪21世纪教育网有
12.如图,已知直线a∥b,点C,D在直线a上,点A,B在直线b上,线段BC,AD相交于点E,写出图中面积相等的所有三角形: .?
易错点 不注意分情况讨论,造成漏解
13.在?ABCD中,∠DAB的平分线分边BC为6 cm和5 cm两部分,则?ABCD的周长为 .?【出处:21教育名师】21cnjy.com
提升训练
考查角度1 利用平行四边形边角性质证明线段关系
14.(2016·西宁)如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=FC;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
考查角度2 利用平行四边形边角性质进行计算
15.如图,?ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.21教育名师原创作品21·世纪*教育网
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
探究培优
拔尖角度1 利用平行四边形的定义和性质探究实际问题
16.如图所示的是某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站?请说明理由.【版权所有:21教育】
拔尖角度2 利用平行四边形的定义和性质探究线段的和的问题(归一法)
17. 如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由.21*cnjy*com2-1-c-n-j-y
参考答案
1.【答案】B
解:此题易错在平行四边形数不全.解决的技巧是有序思维,即在思考问题时一定要有顺序.此题可按照平行四边形的组成来数,独立的平行四边形有:四边形AEOH,四边形HOFD,四边形EBNO,四边形ONCF;由两个平行四边形组成的平行四边形有:四边形AEFD,四边形EBCF,四边形ABNH,四边形HNCD;由四个平行四边形组成的平行四边形是四边形ABCD,所以共有9个.21·cn·jy·com2·1·c·n·j·y
2.【答案】C
解:由平行四边形的性质和角平分线的定义得出∠F=∠FCB,所以BF=BC=8,同理,DE=CD=6,求出AF=BF-AB=2,AE=AD-DE=2,即可得出结果.21*cnjy*com
3.【答案】B
解:根据平行四边形对边相等可知BC===12.
4.【答案】C
5.【答案】C
解:A.当BE=DF时,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS),故此选项不符合题意;
B.当BF=DE时,
可得BE=DF,
同选项A可证明△ABE≌△CDF(SAS),故此选项不符合题意;
C.当AE=CF时无法得出△ABE≌△CDF,故此选项符合题意;
D.当∠1=∠2时,
∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),故此选项不符合题意;
故选C.
6.【答案】A
解:由点的坐标特征得出点A和点C关于原点对称,由平行四边形的性质得出点D和点B关于原点对称,即可得出点D的坐标.
7.【答案】A
8.【答案】D
解:因为四边形ABCD为平行四边形,所以AB∥CD.因为∠A=120°,CE⊥AB,所以∠DCB=120°,∠ECD=90°.所以∠BCE=∠DCB-∠ECD=120°-90°=30°.21教育网21·cn·jy·com
9.【答案】C
解:根据∠A与∠C为平行四边形ABCD的对角且∠A+∠C=200°,可知∠A=100°.又∵∠A+∠B=180°,∴∠B=80°.【来源:21·世纪·教育·网】
10.【答案】D
11.【答案】15 cm
12.【答案】△ACB与△ADB,△ACD与△CBD,△ACE与△BDE
13.【答案】32 cm或34 cm
解:情况一,如图①,BE=5 cm,CE=6 cm.
∵四边形ABCD为平行四边形,
∴AD=BC,AB=CD,AD∥BC,
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE=5 cm,
∴平行四边形ABCD的周长=(5+5+6)×2=32(cm).
情况二,如图②,BE=6 cm,CE=5 cm.
同理可得AB=BE=6 cm,
∴平行四边形ABCD的周长=(6+6+5)×2=34(cm).
本题利用了分类讨论思想,AE把BC分成5 cm,6 cm两部分,没有明确哪部分是5 cm,所以分两种情况.www-2-1-cnjy-comwww-2-1-cnjy-com
14.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF.∴∠ABE=∠FCE.
∵E为BC中点,∴BE=CE.
在△ABE与△FCE中,
∴△ABE≌△FCE(ASA).
∴AB=FC.
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF.
∵△ABE≌△FCE,
∴AE=FE.∴DE⊥AF.
15.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE.
在△ODF和△OBE中,
∴△ODF≌△OBE(AAS),
∴BO=DO.
(2)解:∵BD⊥AD,
∴∠ADB=90°,
又∵∠A=45°,
∴△ABD是等腰直角三角形,
∴AD=BD.
∵EF⊥AB,∠A=45°,
∴∠G=∠A=45°,
又∵BD⊥AD,
∴△ODG是等腰直角三角形,
∴DO=DG.
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
又∵∠G=45°,
∴△DFG是等腰直角三角形,
∴DF=FG=1,
∴DG==.
又DO=DG,
∴DO=,由(1)知DO=BO,
∴BD=BO+DO=2DO=2,
又AD=BD,∴AD=2.
16.解:两人同时到达F站.理由如下:
∵BA∥DE,BD∥AE,
∴四边形ABDE是平行四边形.
∴BA=DE,BD=AE,
①且S△ABD=S△ADE.
∵AF∥BC,EC⊥BC,∴EC⊥AF.
∴EF为△ADE的边AD上的高,CF与△ABD的边AD上的高相等.
∴S△ABD=AD·CF,
S△ADE=AD·EF.
∵S△ABD=S△ADE,∴CF=EF.②
∴DF为EC的垂直平分线,
∴DC=DE.
又BA=DE,∴DC=BA.③
由①②③得BA+AE+EF=BD+DC+CF.
又∵两人同时出发,两车速度相同,途中耽误时间相同,∴两人同时到达F站.
17.解:EF+GH+MN=2a,EF+GH+MN的值不随点P位置的改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵GH∥BC,∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形,
∴GH=AG=AM+MG.①
同理△BMN是等边三角形,
∴MN=MB=MG+GB.②
∵MN∥AC,EF∥AB,
∴四边形AMPE是平行四边形,
∴PE=AM.
同理可证四边形BFPG是平行四边形.∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得
EF+GH+MN=(AM+GB)+(AM+MG)+(MG+GB)=2(AM+MG+GB)=2AB=2a,是一个定值,不随点P位置的改变而改变.21世纪教育网21-cn-jy.com
第1课时 平行四边形的边、角性质
基础训练
知识点1 平行四边形的定义
1.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,EF与HN相交于点O,则图中共有平行四边形( )2·1·c·n·j·y21世纪教育网版权所有
A.12个 B.9个 C.7个 D.5个
2.(2016·泰安)如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )21·世纪*教育网
A.2 B.3 C.4 D.6
知识点2 平行四边形的性质——对边相等
3.已知?ABCD的周长为32,AB=4,则BC等于( )
A.4 B.12 C.24 D.28
4.如图,在?ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )2-1-c-n-j-y21教育网
A.1 B.2 C.3 D.4
5.如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )21*cnjy*com【来源:21·世纪·教育·网】
A.BE=DF B.BF=DE
C.AE=CF D.∠1=∠2
6.(2016·福州)在平面直角坐标系中,已知?ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )【来源:21cnj*y.co*m】
A.(-2,1) B.(-2,-1)
C.(-1,-2) D.(-1,2)
知识点3 平行四边形的性质——对角相等
7.(2016·衢州)如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )21cnjy.comwww.21-cn-jy.com
A.45° B.55° C.65° D.75°
8.如图,在?ABCD中,CE⊥AB,E为垂足,如果∠A=120°,那么∠BCE的度数是( )
A.80° B.50° C.40° D.30°
9.已知?ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160° C.80° D.60°
知识点4 平行线之间的距离
10.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法不正确的是( )
A.AB=CD
B.EC=FG
C.A,B两点间的距离就是线段AB的长度
D.a与b的距离就是线段CD的长度
11.如图,在?ABCD中,对角线AC=21 cm,BE⊥AC于E,且BE=5 cm,AD=7 cm,则AD和BC之间的距离为 .?21世纪21世纪教育网有
12.如图,已知直线a∥b,点C,D在直线a上,点A,B在直线b上,线段BC,AD相交于点E,写出图中面积相等的所有三角形: .?
易错点 不注意分情况讨论,造成漏解
13.在?ABCD中,∠DAB的平分线分边BC为6 cm和5 cm两部分,则?ABCD的周长为 .?【出处:21教育名师】21cnjy.com
提升训练
考查角度1 利用平行四边形边角性质证明线段关系
14.(2016·西宁)如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=FC;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
考查角度2 利用平行四边形边角性质进行计算
15.如图,?ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.21教育名师原创作品21·世纪*教育网
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
探究培优
拔尖角度1 利用平行四边形的定义和性质探究实际问题
16.如图所示的是某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站?请说明理由.【版权所有:21教育】
拔尖角度2 利用平行四边形的定义和性质探究线段的和的问题(归一法)
17. 如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由.21*cnjy*com2-1-c-n-j-y
参考答案
1.【答案】B
解:此题易错在平行四边形数不全.解决的技巧是有序思维,即在思考问题时一定要有顺序.此题可按照平行四边形的组成来数,独立的平行四边形有:四边形AEOH,四边形HOFD,四边形EBNO,四边形ONCF;由两个平行四边形组成的平行四边形有:四边形AEFD,四边形EBCF,四边形ABNH,四边形HNCD;由四个平行四边形组成的平行四边形是四边形ABCD,所以共有9个.21·cn·jy·com2·1·c·n·j·y
2.【答案】C
解:由平行四边形的性质和角平分线的定义得出∠F=∠FCB,所以BF=BC=8,同理,DE=CD=6,求出AF=BF-AB=2,AE=AD-DE=2,即可得出结果.21*cnjy*com
3.【答案】B
解:根据平行四边形对边相等可知BC===12.
4.【答案】C
5.【答案】C
解:A.当BE=DF时,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS),故此选项不符合题意;
B.当BF=DE时,
可得BE=DF,
同选项A可证明△ABE≌△CDF(SAS),故此选项不符合题意;
C.当AE=CF时无法得出△ABE≌△CDF,故此选项符合题意;
D.当∠1=∠2时,
∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),故此选项不符合题意;
故选C.
6.【答案】A
解:由点的坐标特征得出点A和点C关于原点对称,由平行四边形的性质得出点D和点B关于原点对称,即可得出点D的坐标.
7.【答案】A
8.【答案】D
解:因为四边形ABCD为平行四边形,所以AB∥CD.因为∠A=120°,CE⊥AB,所以∠DCB=120°,∠ECD=90°.所以∠BCE=∠DCB-∠ECD=120°-90°=30°.21教育网21·cn·jy·com
9.【答案】C
解:根据∠A与∠C为平行四边形ABCD的对角且∠A+∠C=200°,可知∠A=100°.又∵∠A+∠B=180°,∴∠B=80°.【来源:21·世纪·教育·网】
10.【答案】D
11.【答案】15 cm
12.【答案】△ACB与△ADB,△ACD与△CBD,△ACE与△BDE
13.【答案】32 cm或34 cm
解:情况一,如图①,BE=5 cm,CE=6 cm.
∵四边形ABCD为平行四边形,
∴AD=BC,AB=CD,AD∥BC,
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE=5 cm,
∴平行四边形ABCD的周长=(5+5+6)×2=32(cm).
情况二,如图②,BE=6 cm,CE=5 cm.
同理可得AB=BE=6 cm,
∴平行四边形ABCD的周长=(6+6+5)×2=34(cm).
本题利用了分类讨论思想,AE把BC分成5 cm,6 cm两部分,没有明确哪部分是5 cm,所以分两种情况.www-2-1-cnjy-comwww-2-1-cnjy-com
14.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF.∴∠ABE=∠FCE.
∵E为BC中点,∴BE=CE.
在△ABE与△FCE中,
∴△ABE≌△FCE(ASA).
∴AB=FC.
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF.
∵△ABE≌△FCE,
∴AE=FE.∴DE⊥AF.
15.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE.
在△ODF和△OBE中,
∴△ODF≌△OBE(AAS),
∴BO=DO.
(2)解:∵BD⊥AD,
∴∠ADB=90°,
又∵∠A=45°,
∴△ABD是等腰直角三角形,
∴AD=BD.
∵EF⊥AB,∠A=45°,
∴∠G=∠A=45°,
又∵BD⊥AD,
∴△ODG是等腰直角三角形,
∴DO=DG.
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
又∵∠G=45°,
∴△DFG是等腰直角三角形,
∴DF=FG=1,
∴DG==.
又DO=DG,
∴DO=,由(1)知DO=BO,
∴BD=BO+DO=2DO=2,
又AD=BD,∴AD=2.
16.解:两人同时到达F站.理由如下:
∵BA∥DE,BD∥AE,
∴四边形ABDE是平行四边形.
∴BA=DE,BD=AE,
①且S△ABD=S△ADE.
∵AF∥BC,EC⊥BC,∴EC⊥AF.
∴EF为△ADE的边AD上的高,CF与△ABD的边AD上的高相等.
∴S△ABD=AD·CF,
S△ADE=AD·EF.
∵S△ABD=S△ADE,∴CF=EF.②
∴DF为EC的垂直平分线,
∴DC=DE.
又BA=DE,∴DC=BA.③
由①②③得BA+AE+EF=BD+DC+CF.
又∵两人同时出发,两车速度相同,途中耽误时间相同,∴两人同时到达F站.
17.解:EF+GH+MN=2a,EF+GH+MN的值不随点P位置的改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵GH∥BC,∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形,
∴GH=AG=AM+MG.①
同理△BMN是等边三角形,
∴MN=MB=MG+GB.②
∵MN∥AC,EF∥AB,
∴四边形AMPE是平行四边形,
∴PE=AM.
同理可证四边形BFPG是平行四边形.∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得
EF+GH+MN=(AM+GB)+(AM+MG)+(MG+GB)=2(AM+MG+GB)=2AB=2a,是一个定值,不随点P位置的改变而改变.21世纪教育网21-cn-jy.com
