第三章 第一节 图形的平移 课时1同步练习
文档属性
| 名称 | 第三章 第一节 图形的平移 课时1同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 491.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 13:04:06 | ||
图片预览

文档简介
第一节 图形的平移
第1课时 平移的认识
基础检测
知识点1平移的定义
1.在平面内,把一个图形整体沿着某一________移动,会得到一个新的图形,这种移动叫做________.________是运动的一种形式,是图形变换的一种.?21世纪教育网版权所有
2.以下现象:①水管里水的流动;②滑雪运动员在平坦的雪地上滑行;③射出的子弹;④火车在笔直的铁轨上行驶.其中是平移的是( )
A.①② B.①③ C.②③ D.②④
3.在下列四个汽车标志图案中,能用平移变换来分析其形成过程的是( )
4.下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
知识点2平移的性质
5.在平移的过程中,新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是________.连接各组对应点的线段________;?
新图形与原图形上的对应线段________、对应角________?
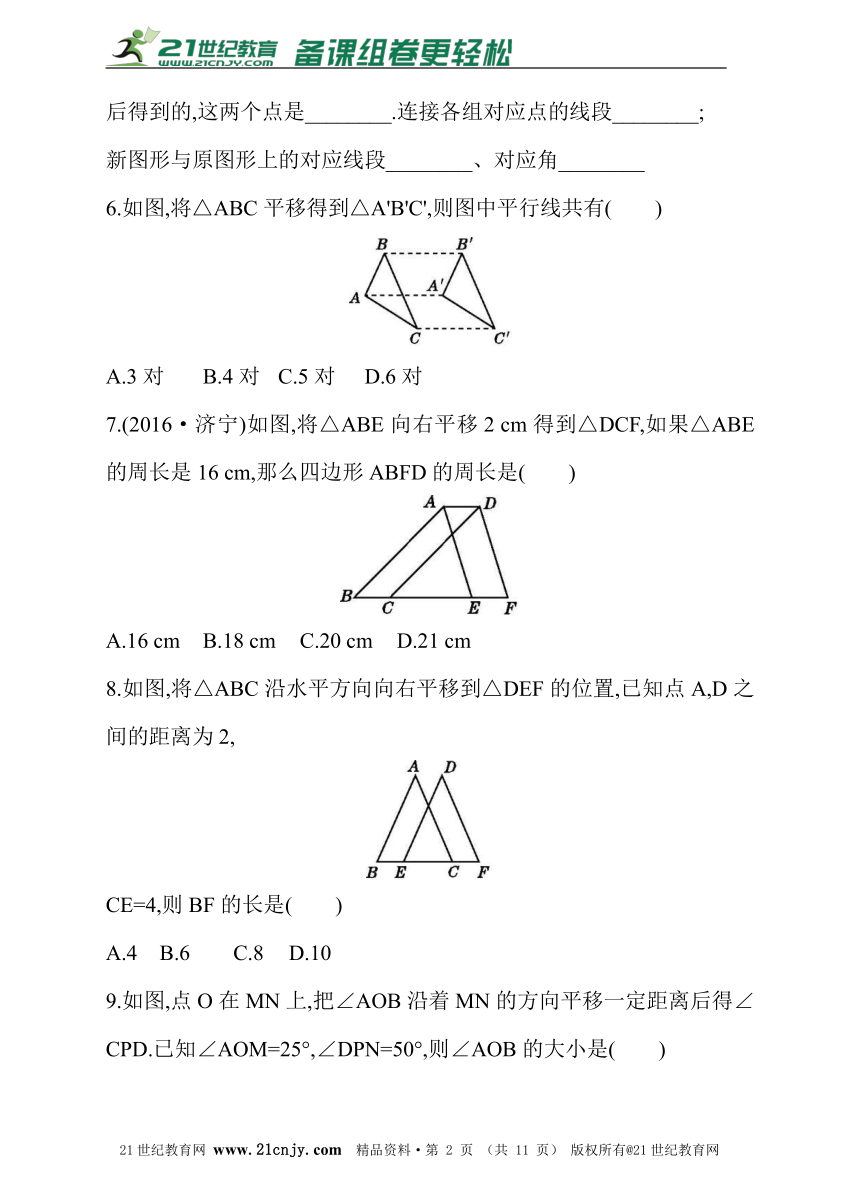
6.如图,将△ABC平移得到△A'B'C',则图中平行线共有( )
A.3对 B.4对 C.5对 D.6对
7.(2016·济宁)如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16 cm,那么四边形ABFD的周长是( )21cnjy.com
A.16 cm B.18 cm C.20 cm D.21 cm
8.如图,将△ABC沿水平方向向右平移到△DEF的位置,已知点A,D之间的距离为2,
CE=4,则BF的长是( )
A.4 B.6 C.8 D.10
9.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的大小是( )
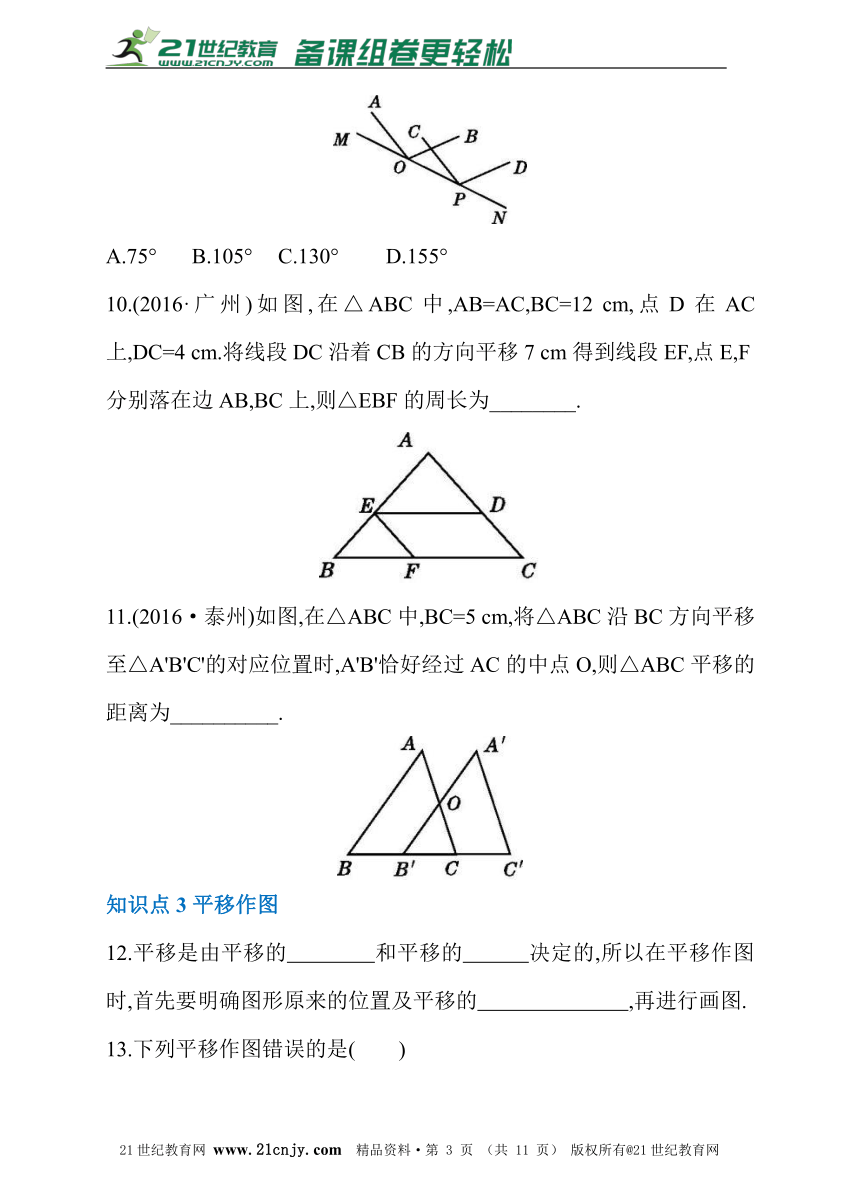
A.75° B.105° C.130° D.155°
10.(2016·广州)如图,在△ABC中,AB=AC,BC=12 cm,点D在AC上,DC=4 cm.将线段DC沿着CB的方向平移7 cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为________.?21·cn·jy·com
11.(2016·泰州)如图,在△ABC中,BC=5 cm,将△ABC沿BC方向平移至△A'B'C'的对应位置时,A'B'恰好经过AC的中点O,则△ABC平移的距离为__________.?www.21-cn-jy.com
知识点3平移作图
12.平移是由平移的 和平移的 决定的,所以在平移作图时,首先要明确图形原来的位置及平移的 ,再进行画图.?
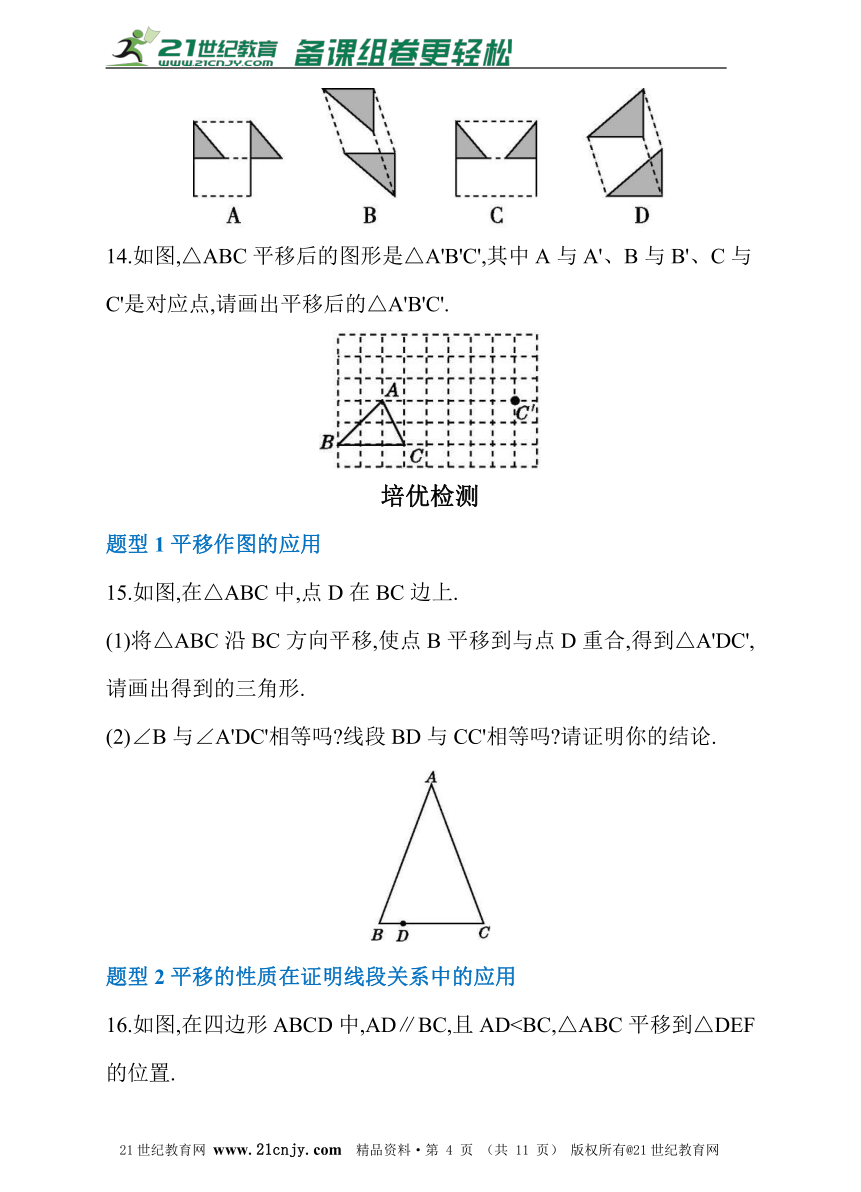
13.下列平移作图错误的是( )
14.如图,△ABC平移后的图形是△A'B'C',其中A与A'、B与B'、C与C'是对应点,请画出平移后的△A'B'C'.【来源:21·世纪·教育·网】
培优检测
题型1平移作图的应用
15.如图,在△ABC中,点D在BC边上.
(1)将△ABC沿BC方向平移,使点B平移到与点D重合,得到△A'DC',请画出得到的三角形.
(2)∠B与∠A'DC'相等吗?线段BD与CC'相等吗?请证明你的结论.
题型2平移的性质在证明线段关系中的应用
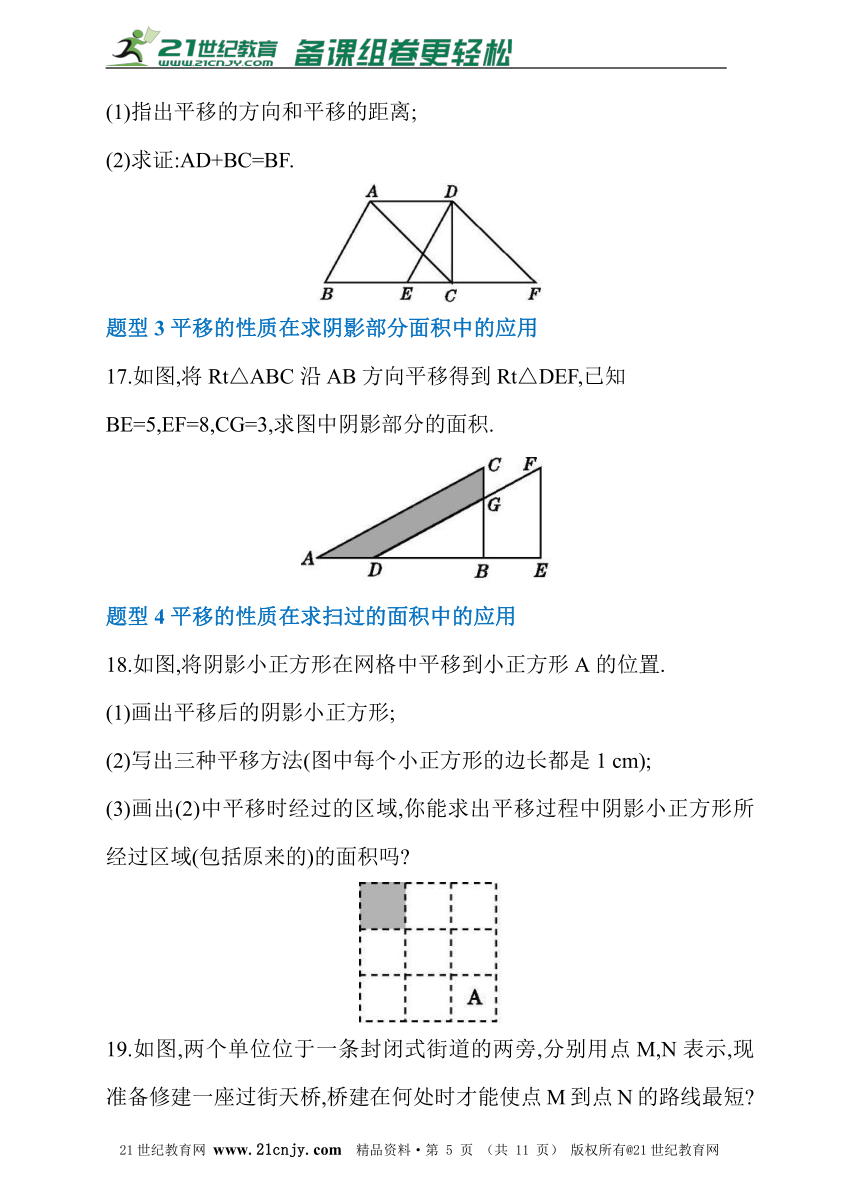
16.如图,在四边形ABCD中,AD∥BC,且AD(1)指出平移的方向和平移的距离;
(2)求证:AD+BC=BF.
题型3平移的性质在求阴影部分面积中的应用
17.如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知
BE=5,EF=8,CG=3,求图中阴影部分的面积.
题型4平移的性质在求扫过的面积中的应用
18.如图,将阴影小正方形在网格中平移到小正方形A的位置.
(1)画出平移后的阴影小正方形;
(2)写出三种平移方法(图中每个小正方形的边长都是1 cm);
(3)画出(2)中平移时经过的区域,你能求出平移过程中阴影小正方形所经过区域(包括原来的)的面积吗?2·1·c·n·j·y
19.如图,两个单位位于一条封闭式街道的两旁,分别用点M,N表示,现准备修建一座过街天桥,桥建在何处时才能使点M到点N的路线最短?请说明理由.(注意:桥必须和街道垂直) 21·世纪*教育网
参考答案
1.【答案】直线方向;平移;平移
2. 【答案】D
解:(1)水管不一定是笔直的,故错误;
(2)符合平移的定义,故正确;
(3)射出的子弹改变了运动方向,不符合平移的定义,故错误;
(4)火车在笔直的铁轨上行使,符合平移的定义,故正确.
所以(2)(4)正确.
故选D.
【答案】D
【答案】C
解:由分析可知:在图形的平移中,下列说法中错误的是:图形上可能存在不动点;故选:C.
5. 【答案】对应点;平行(或在同一条直线上)且相等;平行(或在同一条直线上)且相等;相等
6. 【答案】D
解:∵△ABC平移得到△EFG,A的对应点为E,B的对应点为F,C的对应点为G,
∴AB∥EF,BC∥FG,AC∥EG,AE∥CG,AE∥BF,BF∥CG,共6对.故选D.
【答案】C
解:∵△ABE向右平移2cm得到△DCF,
∴EF=AD=2cm,AE=DF,
∵△ABE的周长为16cm,
∴AB+BE+AE=16cm,
∴四边形ABFD的周长=AB+BE+EF+DF+AD
=AB+BE+AE+EF+AD
=16cm+2cm+2cm
=20cm.
故选C.
【答案】C
解:试题分析:根据平移的基本性质可得BE=CF=AD=2,再结合CE=4即可求得结果.
由题意得BE=CF=AD=2,所以BF=BE+CE+CF=8
故选C.
【答案】B
解:∵∠AOB沿中MN9方向平移一定距离后得∠CPD,
∴BO∥DP,
∴∠BON=∠DPN=50°,
∵∠AOM+∠AOB+∠BON=1y0°,
∴∠AOB=1y0°-55°-50°=105°.
故选B.
10. 【答案】13 cm
11. 【答案】2.5 cm
12. 【答案】方向;距离;方向和距离
13. 【答案】C
14.解:如图所示.
15.解:(1)所作图形如图所示.
(2)相等;相等.
证明:由平移的性质可得∠A'DC'=∠B,BC=DC'.
∵BC=BD+DC,DC'=DC+CC',
∴BD=CC'.
16.(1)解:平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)证明:∵△ABC平移到△DEF的位置,∴CF=AD.
∵CF+BC=BF,∴AD+BC=BF.
17.解:∵Rt△ABC沿AB方向平移得到Rt△DEF,
∴△ABC的面积与△DEF的面积相等,BC=EF.
∴△ABC的面积-△DBG的面积=△DEF的面积-△DBG的面积.
∴阴影部分的面积与梯形GBEF的面积相等.
∵EF=8,CG=3,∴BG=BC-CG=EF-CG=5.
又∵BE=5,
∴阴影部分的面积=(5+8)×5×=32.5.
18.解:(1)如图所示.
(1)题
(2)如图,方法有很多,具体如下(答案不唯一):
图①将阴影小正方形先向右平移2 cm,再向下平移2 cm;
图②将阴影小正方形向右下45°方向平移2 cm;
图③将阴影小正方形先向右平移1 cm,再向下平移2 cm,再向右平移1 cm.
(2)题
(3)如图所示(方法不唯一).∵每个小正方形的边长都为1 cm,∴每个小正方形的面积都是1 cm2.21教育网
(3)题
图①中平移所经过区域的面积是5×1=5(cm2);
图②中平移所经过区域的面积是3×1+×1×1×4=5(cm2);
图③中平移所经过区域的面积是5×1=5(cm2).
19.解:作法如下:
(1)作NE⊥AB于点E,交CD于点F;
(2)在NE上截取NN'=EF;
(3)连接MN',交AB于点P;
(4)过点P作PQ⊥AB,交CD于点Q,如图,则PQ为过街天桥应建的位置.
理由:如图,连接QN.
∵PQ⊥AB,NE⊥AB,∴PQ∥NE.
又∵NN'=EF,EF=PQ,
∴PQ=NN'(相当于将PQ平移到NN').
∴QN=PN'.
∴MP+PN'最短(两点之间线段最短),PQ为定值.
∴桥建在PQ处时才能使点M到点N的路线最短.
第1课时 平移的认识
基础检测
知识点1平移的定义
1.在平面内,把一个图形整体沿着某一________移动,会得到一个新的图形,这种移动叫做________.________是运动的一种形式,是图形变换的一种.?21世纪教育网版权所有
2.以下现象:①水管里水的流动;②滑雪运动员在平坦的雪地上滑行;③射出的子弹;④火车在笔直的铁轨上行驶.其中是平移的是( )
A.①② B.①③ C.②③ D.②④
3.在下列四个汽车标志图案中,能用平移变换来分析其形成过程的是( )
4.下列关于图形平移的说法中,错误的是( )
A.图形上所有点移动的方向都相同
B.图形上所有点移动的距离都相等
C.图形上可能存在不动点
D.对应点所连的线段相等
知识点2平移的性质
5.在平移的过程中,新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是________.连接各组对应点的线段________;?
新图形与原图形上的对应线段________、对应角________?
6.如图,将△ABC平移得到△A'B'C',则图中平行线共有( )
A.3对 B.4对 C.5对 D.6对
7.(2016·济宁)如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16 cm,那么四边形ABFD的周长是( )21cnjy.com
A.16 cm B.18 cm C.20 cm D.21 cm
8.如图,将△ABC沿水平方向向右平移到△DEF的位置,已知点A,D之间的距离为2,
CE=4,则BF的长是( )
A.4 B.6 C.8 D.10
9.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的大小是( )
A.75° B.105° C.130° D.155°
10.(2016·广州)如图,在△ABC中,AB=AC,BC=12 cm,点D在AC上,DC=4 cm.将线段DC沿着CB的方向平移7 cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为________.?21·cn·jy·com
11.(2016·泰州)如图,在△ABC中,BC=5 cm,将△ABC沿BC方向平移至△A'B'C'的对应位置时,A'B'恰好经过AC的中点O,则△ABC平移的距离为__________.?www.21-cn-jy.com
知识点3平移作图
12.平移是由平移的 和平移的 决定的,所以在平移作图时,首先要明确图形原来的位置及平移的 ,再进行画图.?
13.下列平移作图错误的是( )
14.如图,△ABC平移后的图形是△A'B'C',其中A与A'、B与B'、C与C'是对应点,请画出平移后的△A'B'C'.【来源:21·世纪·教育·网】
培优检测
题型1平移作图的应用
15.如图,在△ABC中,点D在BC边上.
(1)将△ABC沿BC方向平移,使点B平移到与点D重合,得到△A'DC',请画出得到的三角形.
(2)∠B与∠A'DC'相等吗?线段BD与CC'相等吗?请证明你的结论.
题型2平移的性质在证明线段关系中的应用
16.如图,在四边形ABCD中,AD∥BC,且AD
(2)求证:AD+BC=BF.
题型3平移的性质在求阴影部分面积中的应用
17.如图,将Rt△ABC沿AB方向平移得到Rt△DEF,已知
BE=5,EF=8,CG=3,求图中阴影部分的面积.
题型4平移的性质在求扫过的面积中的应用
18.如图,将阴影小正方形在网格中平移到小正方形A的位置.
(1)画出平移后的阴影小正方形;
(2)写出三种平移方法(图中每个小正方形的边长都是1 cm);
(3)画出(2)中平移时经过的区域,你能求出平移过程中阴影小正方形所经过区域(包括原来的)的面积吗?2·1·c·n·j·y
19.如图,两个单位位于一条封闭式街道的两旁,分别用点M,N表示,现准备修建一座过街天桥,桥建在何处时才能使点M到点N的路线最短?请说明理由.(注意:桥必须和街道垂直) 21·世纪*教育网
参考答案
1.【答案】直线方向;平移;平移
2. 【答案】D
解:(1)水管不一定是笔直的,故错误;
(2)符合平移的定义,故正确;
(3)射出的子弹改变了运动方向,不符合平移的定义,故错误;
(4)火车在笔直的铁轨上行使,符合平移的定义,故正确.
所以(2)(4)正确.
故选D.
【答案】D
【答案】C
解:由分析可知:在图形的平移中,下列说法中错误的是:图形上可能存在不动点;故选:C.
5. 【答案】对应点;平行(或在同一条直线上)且相等;平行(或在同一条直线上)且相等;相等
6. 【答案】D
解:∵△ABC平移得到△EFG,A的对应点为E,B的对应点为F,C的对应点为G,
∴AB∥EF,BC∥FG,AC∥EG,AE∥CG,AE∥BF,BF∥CG,共6对.故选D.
【答案】C
解:∵△ABE向右平移2cm得到△DCF,
∴EF=AD=2cm,AE=DF,
∵△ABE的周长为16cm,
∴AB+BE+AE=16cm,
∴四边形ABFD的周长=AB+BE+EF+DF+AD
=AB+BE+AE+EF+AD
=16cm+2cm+2cm
=20cm.
故选C.
【答案】C
解:试题分析:根据平移的基本性质可得BE=CF=AD=2,再结合CE=4即可求得结果.
由题意得BE=CF=AD=2,所以BF=BE+CE+CF=8
故选C.
【答案】B
解:∵∠AOB沿中MN9方向平移一定距离后得∠CPD,
∴BO∥DP,
∴∠BON=∠DPN=50°,
∵∠AOM+∠AOB+∠BON=1y0°,
∴∠AOB=1y0°-55°-50°=105°.
故选B.
10. 【答案】13 cm
11. 【答案】2.5 cm
12. 【答案】方向;距离;方向和距离
13. 【答案】C
14.解:如图所示.
15.解:(1)所作图形如图所示.
(2)相等;相等.
证明:由平移的性质可得∠A'DC'=∠B,BC=DC'.
∵BC=BD+DC,DC'=DC+CC',
∴BD=CC'.
16.(1)解:平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)证明:∵△ABC平移到△DEF的位置,∴CF=AD.
∵CF+BC=BF,∴AD+BC=BF.
17.解:∵Rt△ABC沿AB方向平移得到Rt△DEF,
∴△ABC的面积与△DEF的面积相等,BC=EF.
∴△ABC的面积-△DBG的面积=△DEF的面积-△DBG的面积.
∴阴影部分的面积与梯形GBEF的面积相等.
∵EF=8,CG=3,∴BG=BC-CG=EF-CG=5.
又∵BE=5,
∴阴影部分的面积=(5+8)×5×=32.5.
18.解:(1)如图所示.
(1)题
(2)如图,方法有很多,具体如下(答案不唯一):
图①将阴影小正方形先向右平移2 cm,再向下平移2 cm;
图②将阴影小正方形向右下45°方向平移2 cm;
图③将阴影小正方形先向右平移1 cm,再向下平移2 cm,再向右平移1 cm.
(2)题
(3)如图所示(方法不唯一).∵每个小正方形的边长都为1 cm,∴每个小正方形的面积都是1 cm2.21教育网
(3)题
图①中平移所经过区域的面积是5×1=5(cm2);
图②中平移所经过区域的面积是3×1+×1×1×4=5(cm2);
图③中平移所经过区域的面积是5×1=5(cm2).
19.解:作法如下:
(1)作NE⊥AB于点E,交CD于点F;
(2)在NE上截取NN'=EF;
(3)连接MN',交AB于点P;
(4)过点P作PQ⊥AB,交CD于点Q,如图,则PQ为过街天桥应建的位置.
理由:如图,连接QN.
∵PQ⊥AB,NE⊥AB,∴PQ∥NE.
又∵NN'=EF,EF=PQ,
∴PQ=NN'(相当于将PQ平移到NN').
∴QN=PN'.
∴MP+PN'最短(两点之间线段最短),PQ为定值.
∴桥建在PQ处时才能使点M到点N的路线最短.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
