3.2.2 图形的旋转 同步练习

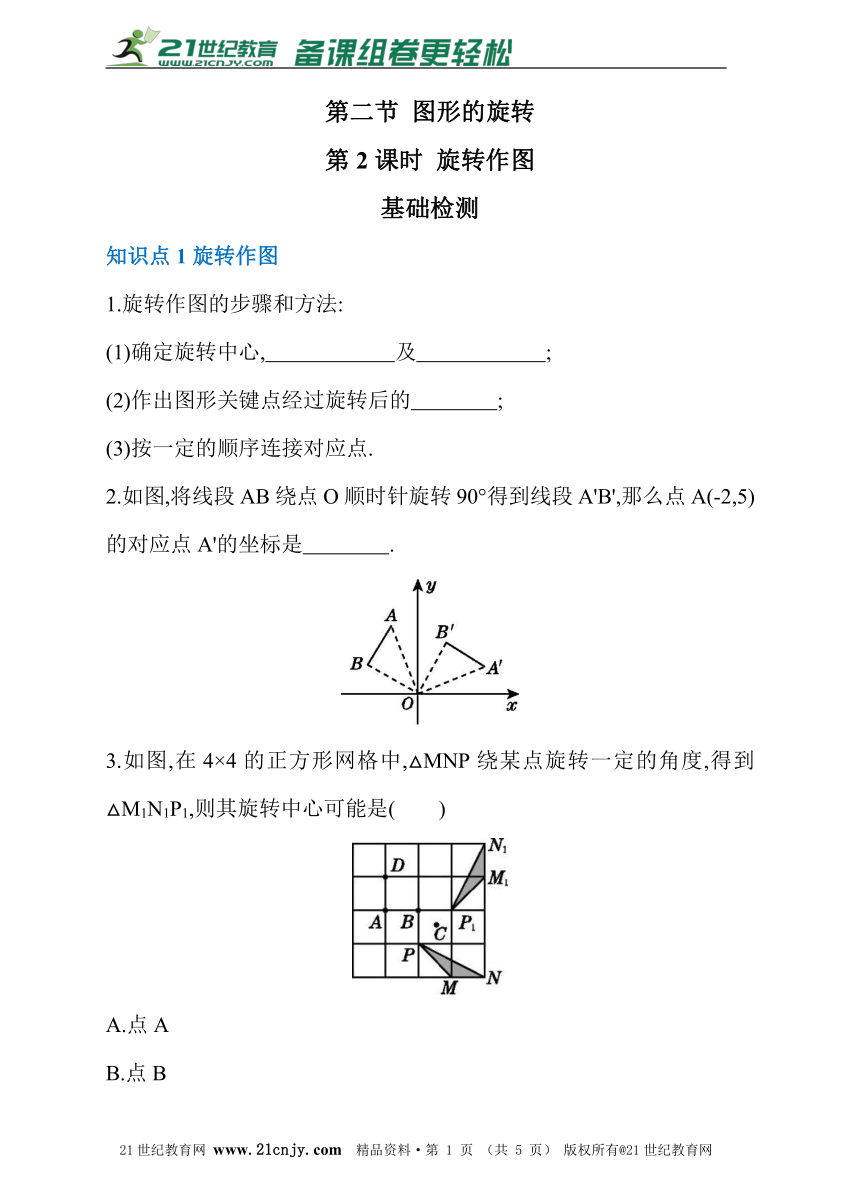
第二节 图形的旋转
第2课时 旋转作图
基础检测
知识点1旋转作图
1.旋转作图的步骤和方法:
(1)确定旋转中心,　　　　　　及　　　　　　;?
(2)作出图形关键点经过旋转后的　　　　;?
(3)按一定的顺序连接对应点.
2.如图,将线段AB绕点O顺时针旋转90°得到线段A'B',那么点A(-2,5)的对应点A'的坐标是　　　　.?21教育网
3.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是(　　)21cnjy.com
A.点A
B.点B
C.点C
D.点D
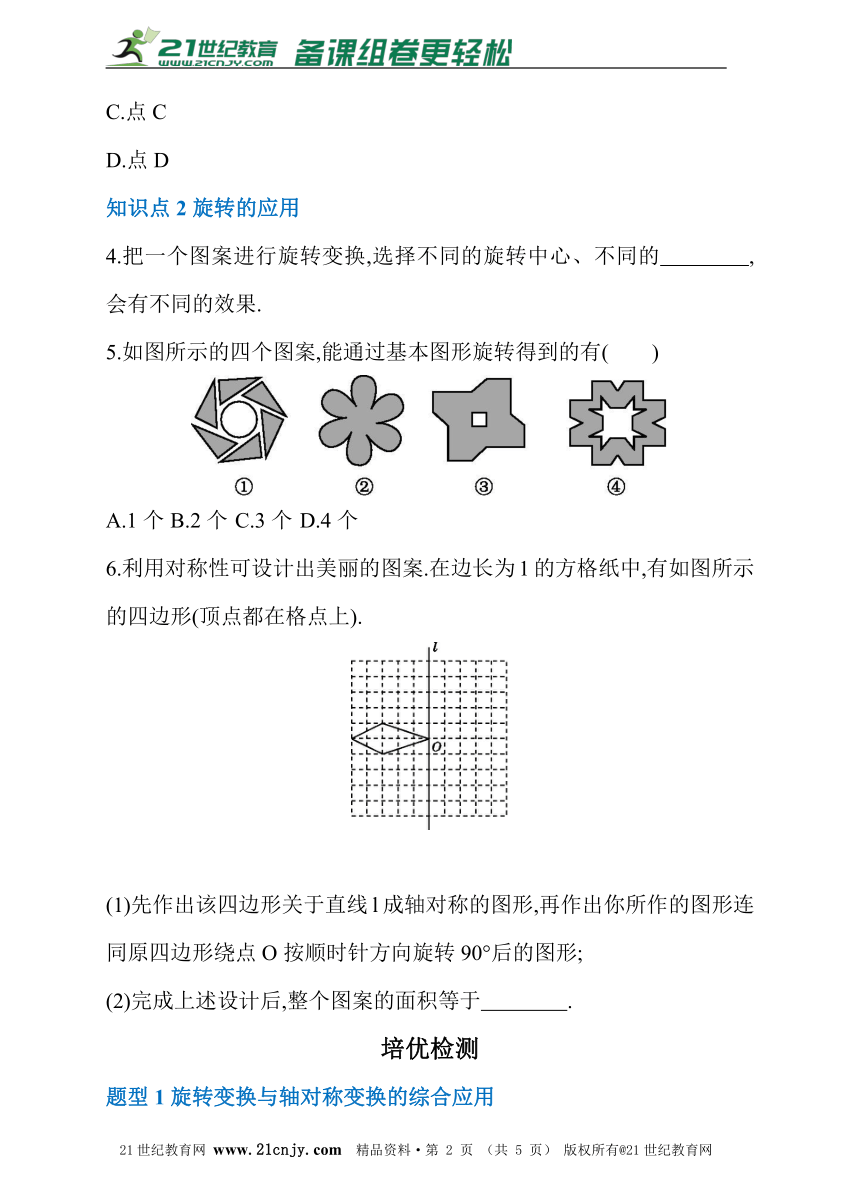
知识点2旋转的应用
4.把一个图案进行旋转变换,选择不同的旋转中心、不同的　　　　,会有不同的效果.?
5.如图所示的四个图案,能通过基本图形旋转得到的有(　　)
A.1个 B.2个 C.3个 D.4个
6.利用对称性可设计出美丽的图案.在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上).
　
(1)先作出该四边形关于直线l成轴对称的图形,再作出你所作的图形连同原四边形绕点O按顺时针方向旋转90°后的图形;21·cn·jy·com
(2)完成上述设计后,整个图案的面积等于　　　　.?
培优检测
题型1旋转变换与轴对称变换的综合应用
7.(2016·齐齐哈尔)如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到的△A2B2O;
(3)在x轴上存在一点P,满足点P到点A1与点A2的距离之和最小,请直接写出P点的坐标.
题型2旋转变换在解题中的应用
8.如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)求证:△COD是等边三角形.
(2)当α=150°时,试判断△AOD的形状.
(3)探究:当α为多少度时,△AOD是等腰三角形?
参考答案
1.【答案】(1)旋转角度;旋转方向　(2)对应点
2. 【答案】(5,2)
3. 【答案】B
解: 根据旋转的性质，知：旋转中心，一定在对应点所连线段的垂直平分线上．
则其旋转中心是NN1和PP1的垂直平分线的交点，即点B．
4. 【答案】旋转角
5. 【答案】D
解: A、B、C、D都可以可以通过旋转，又可以通过轴对称得到，故都正确；选D.
6.解:(1)如图所示.　(2)20
7.解:(1)如图,△A1B1C1为所求作的三角形.
(2)如图,△A2B2O为所求作的三角形.
(3)P点的坐标为.
8.(1)证明:由旋转的性质知△ADC≌△BOC,∴DC=OC.
又∵∠DCO=60°,∴△COD是等边三角形.
(2)解:∵α=∠ADC=150°,∠ODC=60°,∴∠ADO=90°.
∴△AOD是直角三角形.
(3)解:∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,∠
DAO=180°-(190°-α)-(α-60°)=50°.若∠ADO=∠AOD,即α-60°=190°-α,∴α=125°;21世纪教育网版权所有
若∠ADO=∠DAO,即α-60°=50°,∴α=110°;
若∠AOD=∠DAO,即190°-α=50°.∴α=140°.
综上所述,当α=125°或110°或140°时,△AOD是等腰三角形.