3.2.1 图形的旋转 同步练习

第二节 图形的旋转
第1课时 旋转的认识
基础检测
知识点1旋转及相关概念
1.在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动叫做_____,这个定点叫做_____,转动的角叫做_____角.?
2.如图,△AOB绕着点O旋转至△A'OB'的位置,此时:
(1)点B的对应点是_____;?
(2)旋转中心是_____,旋转角为_____;?
(3)∠A的对应角是_____,线段OB的对应线段是线段_____.?
3.(2016·呼和浩特)将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是(　　)
A.96 B.69 C.66 D.99
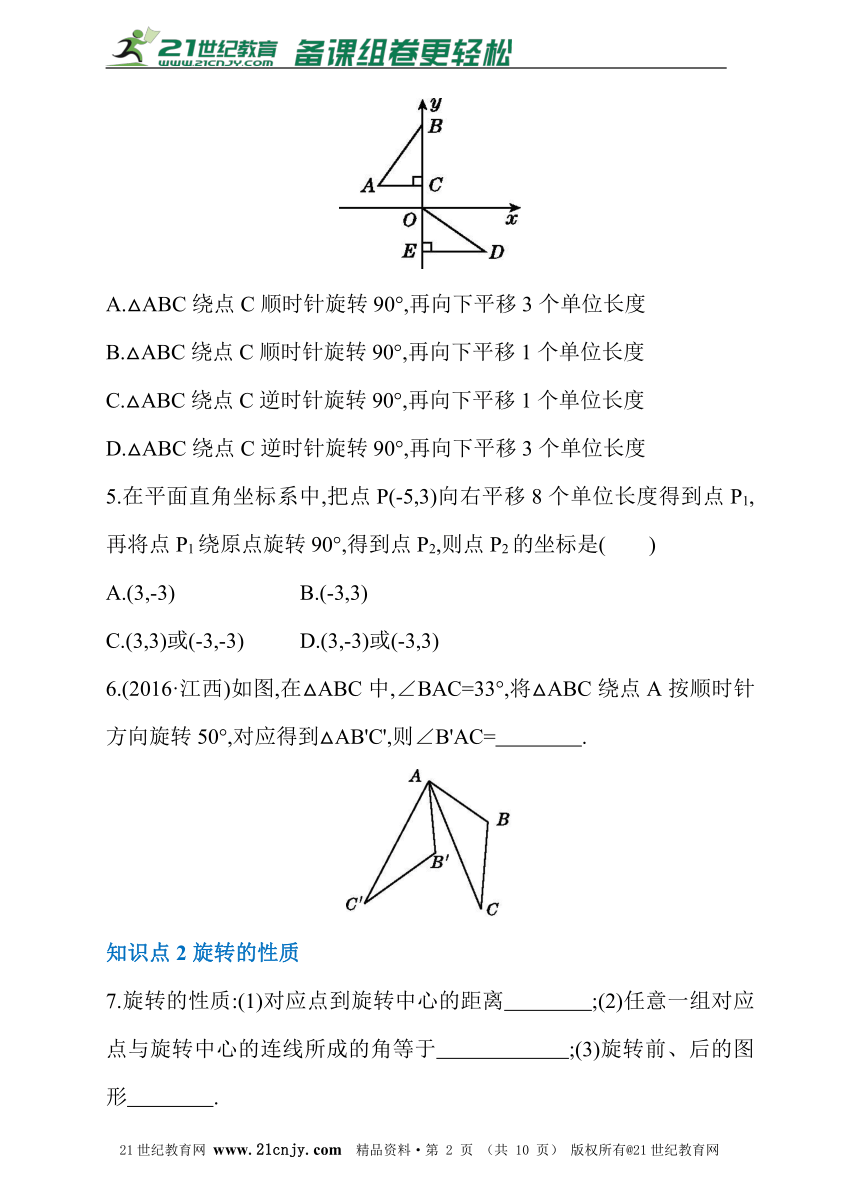
4.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是(　　)
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度
5.在平面直角坐标系中,把点P(-5,3)向右平移8个单位长度得到点P1,再将点P1绕原点旋转90°,得到点P2,则点P2的坐标是(　　)
A.(3,-3) B.(-3,3)
C.(3,3)或(-3,-3) D.(3,-3)或(-3,3)
6.(2016·江西)如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC=　　　　.?21·世纪*教育网
知识点2旋转的性质
7.旋转的性质:(1)对应点到旋转中心的距离　　　　;(2)任意一组对应点与旋转中心的连线所成的角等于　　　　　　;(3)旋转前、后的图形　　　　.?21教育网
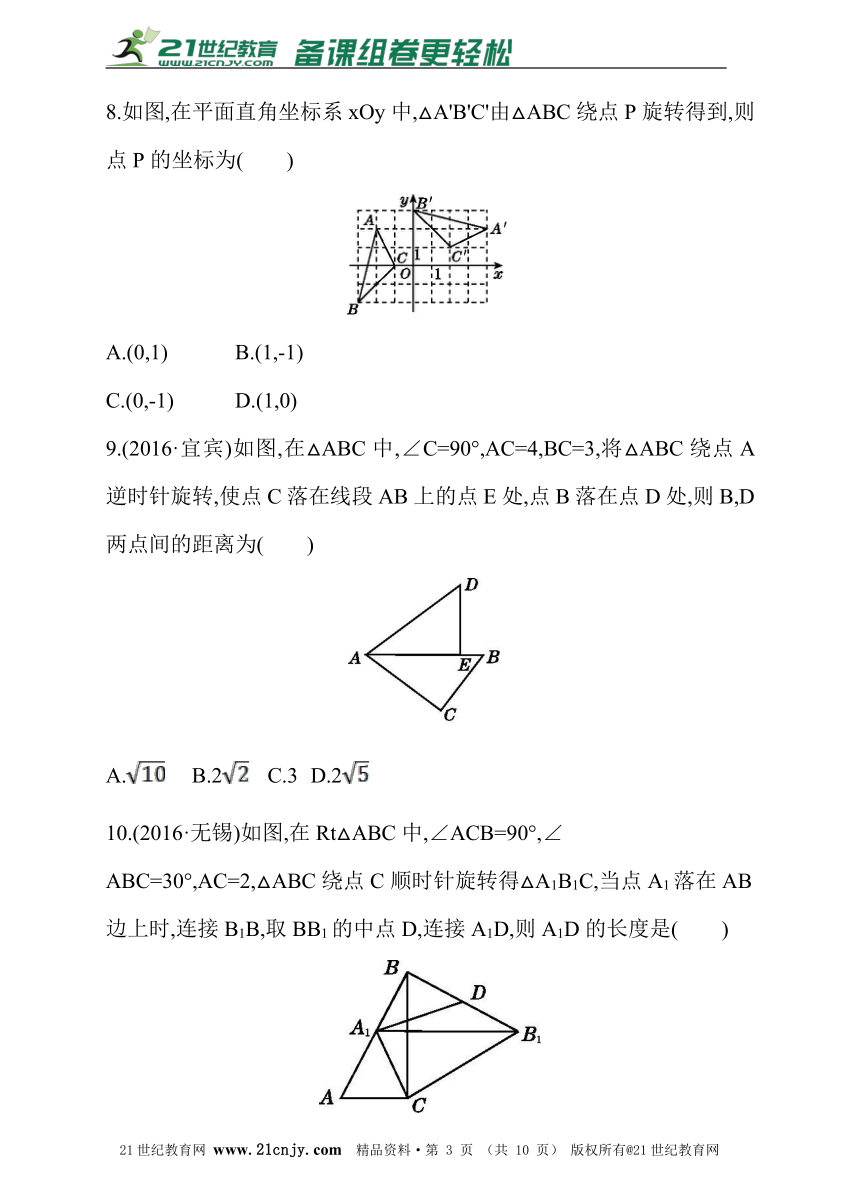
8.如图,在平面直角坐标系xOy中,△A'B'C'由△ABC绕点P旋转得到,则点P的坐标为(　　)
A.(0,1)　　 B.(1,-1)
C.(0,-1) D.(1,0)
9.(2016·宜宾)如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为(　　)21世纪教育网版权所有
A. B.2 C.3 D.2
10.(2016·无锡)如图,在Rt△ABC中,∠ACB=90°,∠
ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当点A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是(　　)
A. B.2 C.3 D.2
11.如图,在△ABO中,AB⊥OB,OB=,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为(　　)www.21-cn-jy.com
A.(-1,) 　　　 B.(-1,)或(1,-)
C.(-1,-) 　　　 D.(-1,-)或(-,-1)
培优检测
题型1旋转的性质在求角中的应用
12.(2016·荆门)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.　【来源：21·世纪·教育·网】
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
题型2旋转的性质在判定图形形状中的应用
13.如图,P为等边三角形ABC内部一点,△ABP旋转后能与△CBP'重合.
(1)旋转中心是哪一点?旋转角是多少度?
(2)连接PP',△BPP'是什么三角形?并说明你的理由.
14.问题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系. 2-1-c-n-j-y
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG的位置,从而发现EF=BE+FD,请你利用图①证明上述结论.　21*cnjy*com
【类比引申】
如图②,在四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E,F分别在边BC,CD上,则当∠EAF与∠BAD满足　　　　　　　关系时,仍有EF=BE+FD.请说明理由.?www-2-1-cnjy-com
【探究应用】
如图③,在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80 m,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC,CD上分别有景点E,F,且AE⊥AD,DF=40(-1)m,现要在E,F之间修一条笔直的道路,求这条道路EF的长(结果精确到1 m,参考数据:≈1.41,≈1.73).
参考答案
1.【答案】旋转;旋转中心;旋转
2. 【答案】(1)点B'　(2)点O;∠AOA'或∠BOB'　(3)∠A';OB'
3. 【答案】B　
解：将两位数“69”看作整体，旋转180°，得到的数字是69．
4. 【答案】A　
5. 【答案】D　
6. 【答案】17°
7. 【答案】(1)相等　(2)旋转角　(3)全等　
8.【答案】B
9. 【答案】A
解：∵在△ABC中，∠C=90°，AC=4，BC=3，
∴AB=5，
∵将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，
∴AE=4，DE=3，
∴BE=1，
在Rt△BED中，
BD==．
故选：A．
10. 【答案】A
11. 【答案】B
12.(1)解:补全图形,如图所示.
(2)证明:由旋转的性质得:∠DCF=90°,DC=FC,BC=EC,∴∠DCE+∠ECF=90°.21cnjy.com
∵∠ACB=90°,
∴∠DCE+∠BCD=90°.
∴∠ECF=∠BCD.
∵EF∥DC,
∴∠EFC+∠DCF=180°.
∴∠EFC=90°,
在△BDC和△EFC中,
∴△BDC≌△EFC(SAS).
∴∠BDC=∠EFC=90°.
13.解:(1)旋转中心是点B,旋转角是60°.
(2)△BPP'是等边三角形.理由:由题意知△ABP绕点B顺时针旋转60°后得到△CBP',∴BP=BP',∠PBP'=60°.∴△BPP'是等边三角形.
14.【发现证明】证明:由旋转的性质可得AE=AG,BE=DG,∠B=∠ADG=90°, ∠EAG=90°.21·cn·jy·com
∵∠B+∠ADC=180°,
∴∠ADC+∠ADG=180°.
∴G,D,C三点共线.
∵∠EAF=45°,∴∠GAF=45°,
∴∠GAF=∠EAF.
又∵AF=AF,∴△AFG≌△AFE(SAS).
∴GF=EF.
∵GF=DG+FD=BE+FD,
∴EF=BE+FD.
【类比引申】解:∠EAF=∠BAD
理由:如图①,将△ABE绕点A逆时针旋转至△ADG的位置,由旋转的性质可得AE=AG,BE=DG,∠B=∠ADG, ∠BAE=∠DAG.
∵∠B+∠ADC=180°,∴∠ADC+∠ADG=180°.
∴G,D,C三点共线.
∵∠BAE=∠DAG,∴∠BAD=∠EAG.
∵∠EAF=∠BAD,∴∠GAF=∠EAF.
又∵AF=AF,∴△AFG≌△AFE(SAS).
∴GF=EF.
∵GF=DG+FD=BE+FD,∴EF=BE+FD.
故答案为∠EAF=∠BAD.
【探究应用】解:∵AE⊥AD,∴∠DAE=90°.
∵∠BAD=150°,∴∠BAE=60°.
又∵∠B=60°,∴△ABE是等边三角形.
∴BE=AB=80 m.
如图②,连接AF,过点A作AH⊥CD交CD的延长线于H.
在Rt△AHD中,∠ADH=180°-∠ADC=60°,AD=80 m,
∴∠HAD=30°.
∴HD=AD=40 m,∴AH==40 m.
∵DF=40(-1) m,∴HF=HD+DF=40+40(-1)=40(m).
∴在Rt△AHF中,AH=HF,∴∠HAF=45°.∴∠DAF=15°.
∴∠EAF=90°-15°=75°.∴∠EAF=∠BAD.
运用上面的结论可得EF=BE+DF=80+40(-1)=40+40≈109(m).即这条道路EF的长约为109 m.2·1·c·n·j·y