18.2 .1 矩形的判定 同步练习
图片预览


文档简介
18.2 特殊的平行四边形
第2课时 矩形的判定
基础训练
知识点1 由对角线的关系判定矩形
1.(2016·黑龙江)如图,在?ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你添加一个条件,使四边形DBCE是矩形.
2.下列四边形:①对角线互相平分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线互相平分且相等的四边形.其中一定是矩形的个数是( )www.21-cn-jy.com
A.1个 B.2个
C.3个 D.4个
3.在?ABCD中,对角线AC,BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是( )2·1·c·n·j·y
A.AB=AD B.OA=OB
C.AC=BD D.DC⊥BC
知识点2 由直角的个数判定矩形
4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AC⊥BD
C.∠ABC=∠BAD
D.∠1=∠2
5.对于四边形ABCD,给出下列6组条件:
①∠A=90°,∠B=∠C=∠D;
②∠A=∠B=90°,∠C=∠D;
③∠A=∠B=∠C=∠D;
④∠A=∠B=∠C=90°;
⑤AC=BD;
⑥AB∥CD,AD∥BC.
其中能得到“四边形ABCD是矩形”的有( )
A.1组 B.2组 C.3组 D.4组
6.在?ABCD中,添加下列条件中的一个,就能判定它是矩形的是( )
A.∠A+∠C=180° B.AB=BC
C.AC⊥BD D.AC=2AB
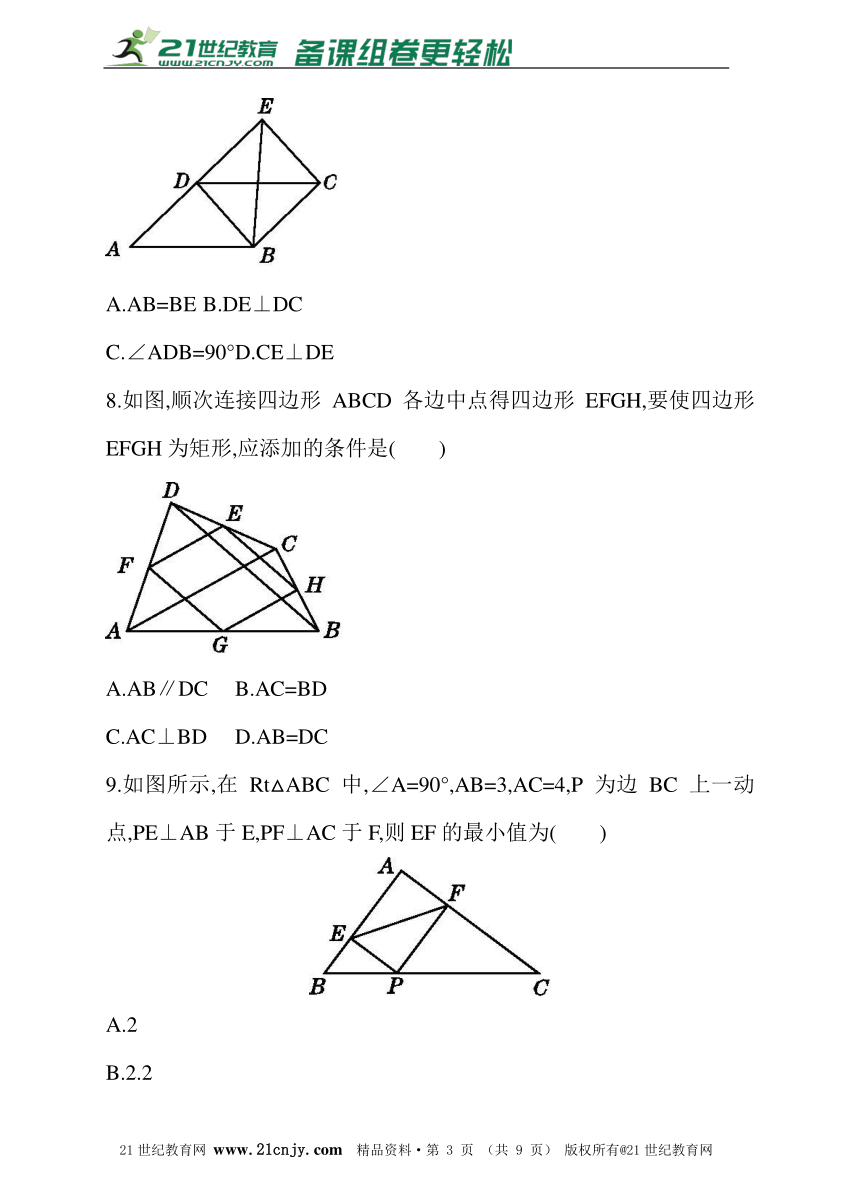
7.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC
C.∠ADB=90° D.CE⊥DE
8.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )21cnjy.com
A.AB∥DC B.AC=BD
C.AC⊥BD D.AB=DC
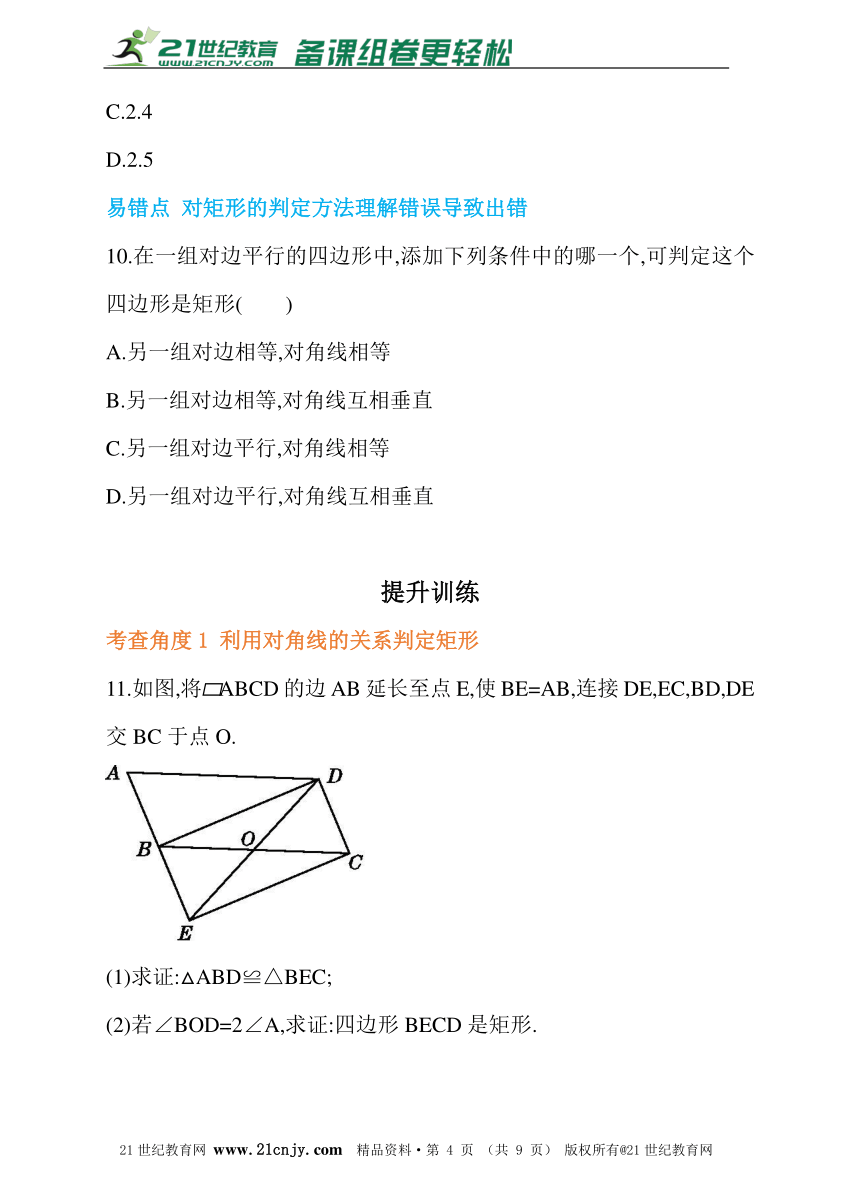
9.如图所示,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.2
B.2.2
C.2.4
D.2.5
易错点 对矩形的判定方法理解错误导致出错
10.在一组对边平行的四边形中,添加下列条件中的哪一个,可判定这个四边形是矩形( )
A.另一组对边相等,对角线相等
B.另一组对边相等,对角线互相垂直
C.另一组对边平行,对角线相等
D.另一组对边平行,对角线互相垂直
提升训练
考查角度1 利用对角线的关系判定矩形
11.如图,将?ABCD的边AB延长至点E,使BE=AB,连接DE,EC,BD,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
考查角度2 利用直角的个数判定矩形
12.如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:
(1)△ADE≌△CBF;
(2)四边形DEBF为矩形.
探究培优
拔尖角度1 利用矩形的性质和判定探究面积关系(作差法)
13.(2016·台州)如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形PEDH和四边形PFBG都是矩形,并写出它们面积之间的关系.
拔尖角度2 利用矩形的判定探究动点的位置(逆向思维法)
14.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F. 21世纪教育网版权所有
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
参考答案
1.【答案】EB=DC
解:利用平行四边形的性质与判定得到四边形DBCE为平行四边形,结合矩形的判定来添加条件即可,本题答案不唯一.21教育网
2.【答案】B 3.【答案】A 4.【答案】C 5.【答案】D
6.【答案】A
解:由平行四边形的对角相等,知∠A=∠C,再结合∠A+∠C=180°,可求出∠C=90°.根据有一个角是直角的平行四边形是矩形,可判定?ABCD是矩形.【来源:21·世纪·教育·网】
7.【答案】B
8.【答案】C
解:此题由中点会想到三角形的中位线,易知EF∥AC∥HG,EH∥BD∥FG,所以四边形EFGH是平行四边形,要使四边形EFGH为矩形,根据矩形的判定(有一个角为直角的平行四边形是矩形),可知当AC⊥BD时,∠EFG=90°,因此四边形EFGH为矩形.故选C.21·世纪*教育网
9.【答案】C 10.【答案】C
11.证明:(1)在平行四边形ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,∴BE=DC.
∴四边形BECD为平行四边形.
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS).
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,
∴∠A=∠BCD.即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC.∴OC=OD.
∴OC+OB=OD+OE,即BC=ED.
∴四边形BECD为矩形.
12.证明:(1)∵四边形ABCD是平行四边形,∴∠A=∠C,AD=BC.
又∵DE⊥AB,BF⊥CD,
∴∠DEA=∠BFC=90°.
∴△ADE≌△CBF.
(2)∵△ADE≌△CBF,∴AE=CF.
∵CD=AB,∴DF=BE.
又∵CD∥AB,
∴四边形DEBF为平行四边形.
又∵∠DEB=90°,
∴四边形DEBF为矩形.
13.证明:(1)∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC.
∵PF∥AB,PH∥AD,
∴PF∥CD,PH∥BC.
∴∠CPF=∠PCH,∠PCF=∠CPH.
在△PHC和△CFP中,
∴△PHC≌△CFP(ASA).
(2)∵四边形ABCD为矩形,
∴∠D=∠B=90°,S△ACD=S△CAB.
又∵EF∥AB∥CD,GH∥AD∥BC,
∴四边形PEDH、四边形PFBG、四边形PEAG和四边形PFCH都是矩形.
∴S△APE=S△PAG,S△PCH=S△CPF.
∴S△ACD-S△APE-S△PCH=S△CAB-S△PAG-S△CPF,即S矩形PEDH=S矩形PFBG.
14.(1)证明:∵CF平分∠ACD,且MN∥BD,
∴∠ACF=∠FCD=∠CFO.
∴OF=OC.
同理,得OC=OE,∴OE=OF.
(2)解:∵∠ACB+∠ACD=180°,CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ECO+∠OCF=∠ACB+∠ACD=(∠ACB+∠ACD)=90°.∴EF===13,21·cn·jy·com
由(1)知,OE=OF,∴OC=EF,
∴OC=.
(3)解:当点O运动到AC的中点时,四边形AECF为矩形.理由如下:
由(1)知OE=OF.当点O运动到AC的中点时,有OA=OC,
∴四边形AECF为平行四边形.
又∵∠ECF=90°,
∴四边形AECF为矩形.
第2课时 矩形的判定
基础训练
知识点1 由对角线的关系判定矩形
1.(2016·黑龙江)如图,在?ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你添加一个条件,使四边形DBCE是矩形.
2.下列四边形:①对角线互相平分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线互相平分且相等的四边形.其中一定是矩形的个数是( )www.21-cn-jy.com
A.1个 B.2个
C.3个 D.4个
3.在?ABCD中,对角线AC,BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是( )2·1·c·n·j·y
A.AB=AD B.OA=OB
C.AC=BD D.DC⊥BC
知识点2 由直角的个数判定矩形
4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AC⊥BD
C.∠ABC=∠BAD
D.∠1=∠2
5.对于四边形ABCD,给出下列6组条件:
①∠A=90°,∠B=∠C=∠D;
②∠A=∠B=90°,∠C=∠D;
③∠A=∠B=∠C=∠D;
④∠A=∠B=∠C=90°;
⑤AC=BD;
⑥AB∥CD,AD∥BC.
其中能得到“四边形ABCD是矩形”的有( )
A.1组 B.2组 C.3组 D.4组
6.在?ABCD中,添加下列条件中的一个,就能判定它是矩形的是( )
A.∠A+∠C=180° B.AB=BC
C.AC⊥BD D.AC=2AB
7.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC
C.∠ADB=90° D.CE⊥DE
8.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )21cnjy.com
A.AB∥DC B.AC=BD
C.AC⊥BD D.AB=DC
9.如图所示,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.2
B.2.2
C.2.4
D.2.5
易错点 对矩形的判定方法理解错误导致出错
10.在一组对边平行的四边形中,添加下列条件中的哪一个,可判定这个四边形是矩形( )
A.另一组对边相等,对角线相等
B.另一组对边相等,对角线互相垂直
C.另一组对边平行,对角线相等
D.另一组对边平行,对角线互相垂直
提升训练
考查角度1 利用对角线的关系判定矩形
11.如图,将?ABCD的边AB延长至点E,使BE=AB,连接DE,EC,BD,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
考查角度2 利用直角的个数判定矩形
12.如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:
(1)△ADE≌△CBF;
(2)四边形DEBF为矩形.
探究培优
拔尖角度1 利用矩形的性质和判定探究面积关系(作差法)
13.(2016·台州)如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形PEDH和四边形PFBG都是矩形,并写出它们面积之间的关系.
拔尖角度2 利用矩形的判定探究动点的位置(逆向思维法)
14.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F. 21世纪教育网版权所有
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
参考答案
1.【答案】EB=DC
解:利用平行四边形的性质与判定得到四边形DBCE为平行四边形,结合矩形的判定来添加条件即可,本题答案不唯一.21教育网
2.【答案】B 3.【答案】A 4.【答案】C 5.【答案】D
6.【答案】A
解:由平行四边形的对角相等,知∠A=∠C,再结合∠A+∠C=180°,可求出∠C=90°.根据有一个角是直角的平行四边形是矩形,可判定?ABCD是矩形.【来源:21·世纪·教育·网】
7.【答案】B
8.【答案】C
解:此题由中点会想到三角形的中位线,易知EF∥AC∥HG,EH∥BD∥FG,所以四边形EFGH是平行四边形,要使四边形EFGH为矩形,根据矩形的判定(有一个角为直角的平行四边形是矩形),可知当AC⊥BD时,∠EFG=90°,因此四边形EFGH为矩形.故选C.21·世纪*教育网
9.【答案】C 10.【答案】C
11.证明:(1)在平行四边形ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,∴BE=DC.
∴四边形BECD为平行四边形.
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS).
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,
∴∠A=∠BCD.即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC.∴OC=OD.
∴OC+OB=OD+OE,即BC=ED.
∴四边形BECD为矩形.
12.证明:(1)∵四边形ABCD是平行四边形,∴∠A=∠C,AD=BC.
又∵DE⊥AB,BF⊥CD,
∴∠DEA=∠BFC=90°.
∴△ADE≌△CBF.
(2)∵△ADE≌△CBF,∴AE=CF.
∵CD=AB,∴DF=BE.
又∵CD∥AB,
∴四边形DEBF为平行四边形.
又∵∠DEB=90°,
∴四边形DEBF为矩形.
13.证明:(1)∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC.
∵PF∥AB,PH∥AD,
∴PF∥CD,PH∥BC.
∴∠CPF=∠PCH,∠PCF=∠CPH.
在△PHC和△CFP中,
∴△PHC≌△CFP(ASA).
(2)∵四边形ABCD为矩形,
∴∠D=∠B=90°,S△ACD=S△CAB.
又∵EF∥AB∥CD,GH∥AD∥BC,
∴四边形PEDH、四边形PFBG、四边形PEAG和四边形PFCH都是矩形.
∴S△APE=S△PAG,S△PCH=S△CPF.
∴S△ACD-S△APE-S△PCH=S△CAB-S△PAG-S△CPF,即S矩形PEDH=S矩形PFBG.
14.(1)证明:∵CF平分∠ACD,且MN∥BD,
∴∠ACF=∠FCD=∠CFO.
∴OF=OC.
同理,得OC=OE,∴OE=OF.
(2)解:∵∠ACB+∠ACD=180°,CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ECO+∠OCF=∠ACB+∠ACD=(∠ACB+∠ACD)=90°.∴EF===13,21·cn·jy·com
由(1)知,OE=OF,∴OC=EF,
∴OC=.
(3)解:当点O运动到AC的中点时,四边形AECF为矩形.理由如下:
由(1)知OE=OF.当点O运动到AC的中点时,有OA=OC,
∴四边形AECF为平行四边形.
又∵∠ECF=90°,
∴四边形AECF为矩形.
