18.2.3 正方形及其性质 同步练习
文档属性
| 名称 | 18.2.3 正方形及其性质 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 459.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:13:20 | ||
图片预览


文档简介
18.2 特殊的平行四边形
第5课时 正方形及其性质
基础训练
知识点1 正方形的定义
1.下面四个定义中不正确的是( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
2.下列说法错误的是( )
A.正方形是平行四边形 B.正方形是菱形
C.正方形是矩形 D.菱形和矩形都是正方形
3.已知,在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )21·cn·jy·com
A.∠D=90° B.AB=CD
C.AD=BC D.BC=CD
知识点2 正方形边的性质
4.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.四条边相等
C.对角线相等 D.对角线互相平分
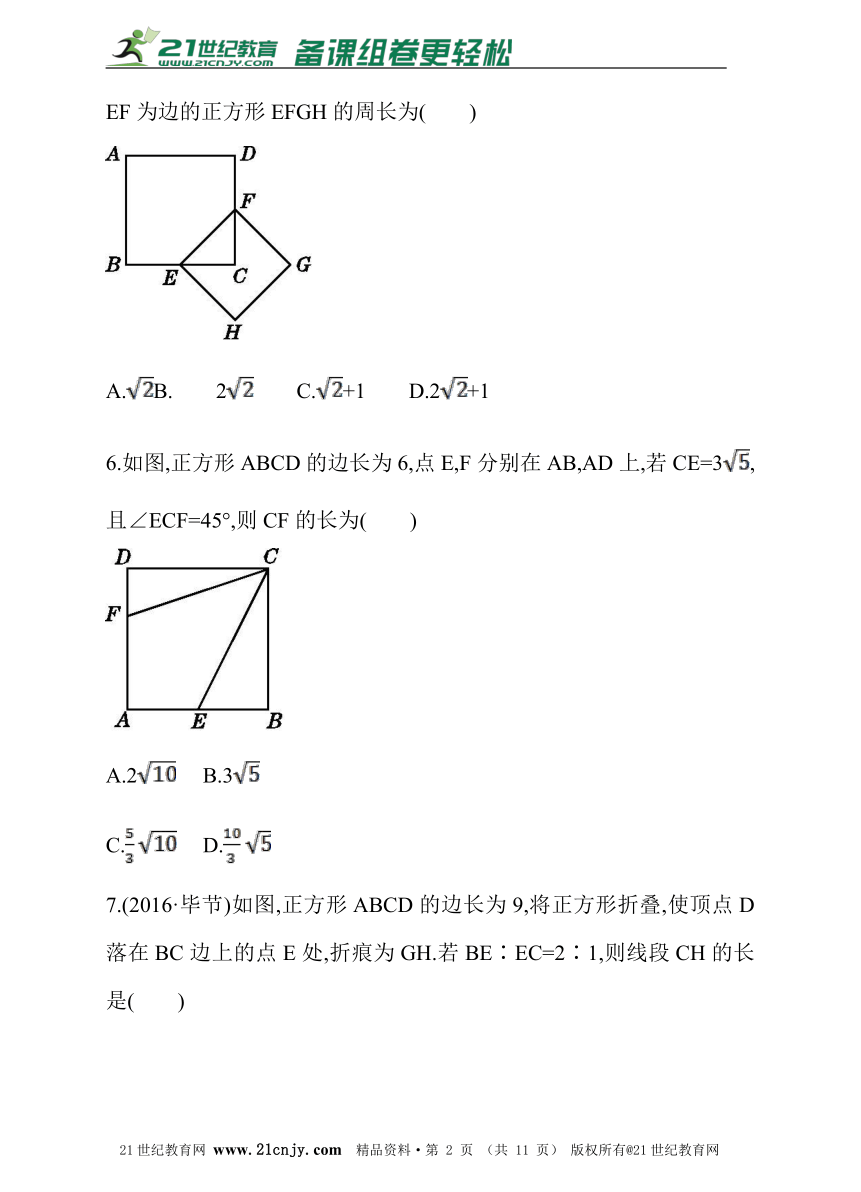
5.(2016·广东)如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )【来源:21·世纪·教育·网】
A.B. 2 C.+1 D.2+1
6.如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为( )21·世纪*教育网
A.2 B.3
C. D.
7.(2016·毕节)如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )www-2-1-cnjy-com
A.3 B.4 C.5 D.6
知识点3 正方形角的性质
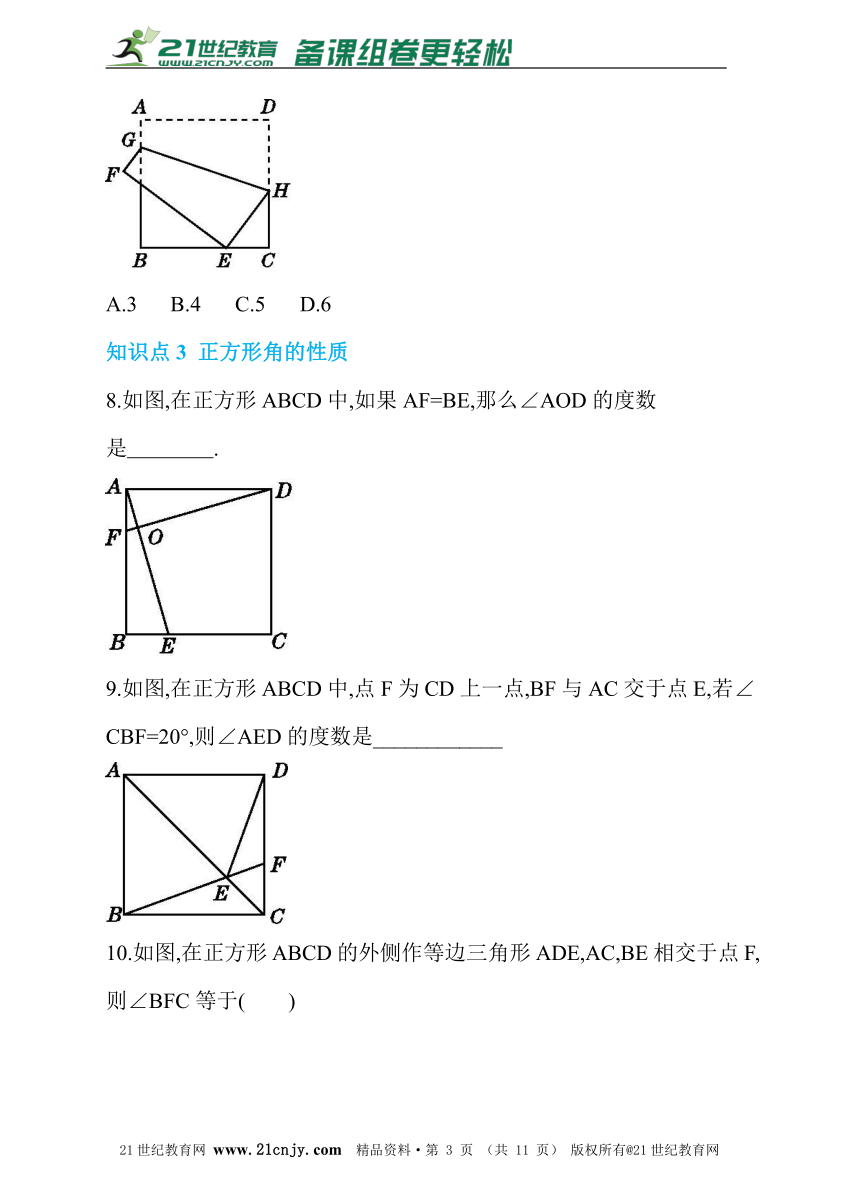
8.如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数
是 .?
9.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED的度数是____________?2-1-c-n-j-y
10.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC等于( )
A.45° B.55° C.60° D.75°
易错点 不能将两线段和转化为一条线段而致错
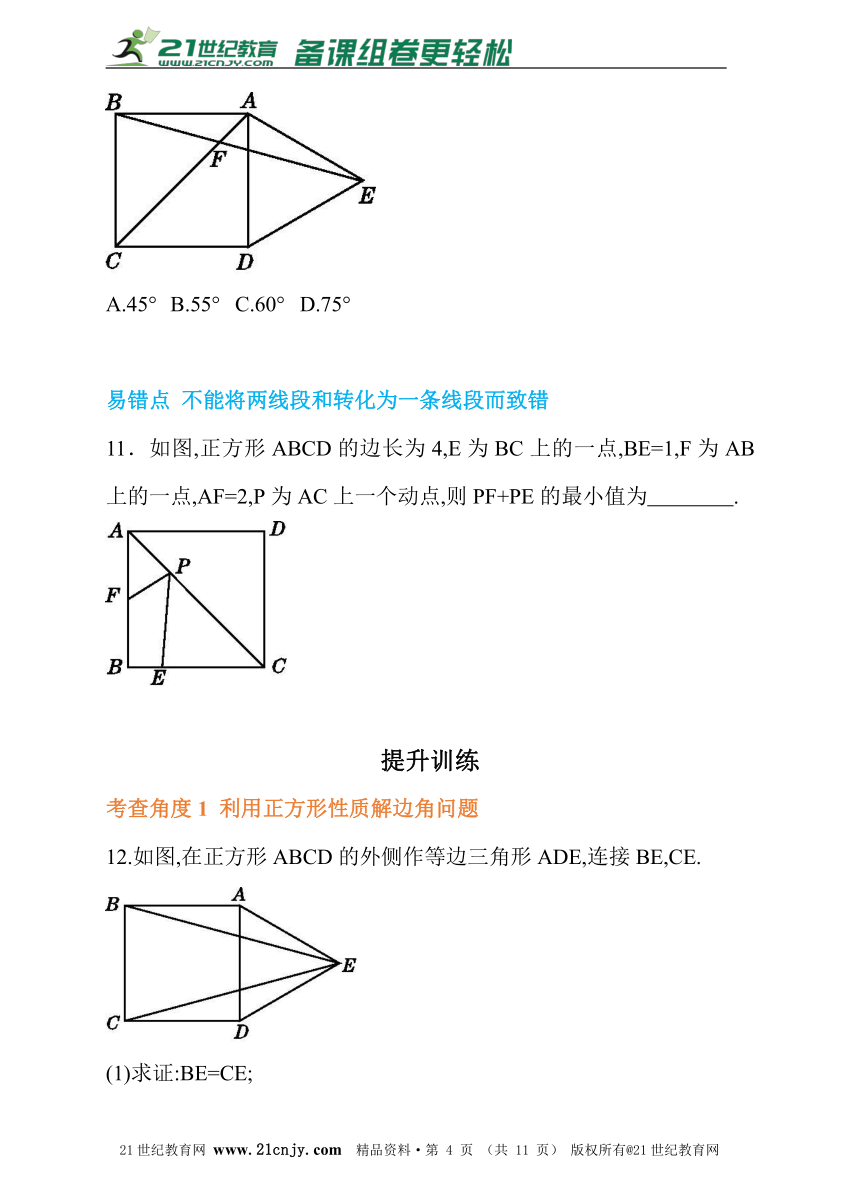
11.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .?
提升训练
考查角度1 利用正方形性质解边角问题
12.如图,在正方形ABCD的外侧作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE;
(2)求∠BEC的度数.
考查角度2 利用正方形性质判定图形形状
13.(2016·贵阳)如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE,CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
探究培优
拔尖角度1 利用三角形、正方形的性质探究两线段间的关系
14.如图①,在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 .?
(2)如图②,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并说明理由.21cnjy.com
(3)若△ADE和△DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.21教育网
拔尖角度2 利用正方形的性质探究改变条件时的结论情况(类比思想)
15.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F. www.21-cn-jy.com
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.21世纪教育网版权所有
参考答案
1.【答案】B 2.【答案】D 3.【答案】D 4.【答案】B
5.【答案】B
解:由正方形的性质和已知条件得出BC=CD=1,∠BCD=90°,CE=CF=,所以△CEF是等腰直角三角形.再利用勾股定理求出EF的长,即可得出正方形EFGH的周长.2·1·c·n·j·y
6.【答案】A
解:延长AB至点F',使BF'=DF,连接CF',EF,先证明Rt△CDF≌Rt△CBF',再证明△ECF≌△ECF',得出EF=EF',最后在Rt△AEF中,利用勾股定理、方程思想解决问题.21*cnjy*com
7.【答案】B
解:根据折叠的性质可得DH=EH,在Rt△CEH中,若设CH=x,则DH=EH=9-x,EC=3,可以根据勾股定理列出方程,从而得出CH的长.
8.【答案】90° 9.【答案】65° 10.【答案】C
11.【答案】
解:在AD上取一点M,使得AM=2,连接EM,交AC于点P,易得此时PF+PE的值最小,即EM的长为PF+PE的最小值.过点M作MN⊥BC于N,由题意可知EN=BN-BE=AM-BE=2-1=1,MN=4,所以EM===. 【来源:21cnj*y.co*m】
易错解:此类问题容易出错的地方是不能将两条线段的和转化为一条线段.
方法规律:正方形是特殊的平行四边形,由于正方形是轴对称图形,求线段和的最小值,往往要通过轴对称的方式将同侧两点转化为异侧两点,通过两点间线段最短求得两线段和的最小值.【出处:21教育名师】
12.(1)证明:∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°.
∵三角形ADE为等边三角形,
∴AE=AD=DE,∠EAD=∠EDA=60°.
∴∠BAE=∠CDE=150°.
∴△BAE≌△CDE.∴BE=CE.
(2)解:∵AB=AD,AD=AE,
∴AB=AE.
∴∠ABE=∠AEB.
又∵∠BAE=150°,
∴∠ABE=∠AEB=15°.
同理可得∠CED=15°,
∴∠BEC=60°-15°×2=30°.
13.(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°.
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF.
∴∠ABC-∠CBF=∠EBF-∠CBF.
∴∠ABF=∠CBE.
在△ABF和△CBE中,
有
∴△ABF≌△CBE(SAS).
(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°.
∴∠AFB=180°-∠BFE=135°.
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°.
∴∠CEF=∠CEB-∠FEB=135°-45°=90°.
∴△CEF是直角三角形.
14.解:(1)AF=BE;AF⊥BE
(2)结论成立.
理由:∵四边形ABCD是正方形,
∴BA=AD=DC,∠BAD=∠ADC=90°.
在△EAD和△FDC中,
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,即∠BAE=∠ADF.
在△BAE和△ADF中,
∴△BAE≌△ADF.
∴BE=AF,∠ABE=∠DAF.
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°.
∴AF⊥BE.
(3)结论都能成立.
15.(1)证明:方法一:∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP.
在△ADP和△CDP中,
∴△ADP≌△CDP.∴PA=PC.
∵PA=PE,∴PC=PE.
方法二:∵四边形ABCD是正方形,
∴直线BD是此正方形的一条对称轴,点A,C关于直线BD对称.
又∵P是BD上一点,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)解:∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠CDE=90°.
∴∠E+∠DFE=90°.
∵PA=PE,∴∠PAD=∠E.
又∵△ADP≌△CDP,
∴∠PAD=∠PCD.
∴∠PCD=∠E.
∵∠PFC=∠DFE,∴∠PCD+∠PFC=∠E+∠DFE=90°.
∴∠CPE=90°.
(3)解:CE=AP.理由:
易证△ADP≌△CDP,
∴PA=PC,∠PAD=∠PCD.
∵PA=PE,
∴PC=PE,∠PAE=∠PEA.
∴∠PEA=∠PCD.
∵∠EFC=∠CPE+∠PCD=∠CDE+∠PEA,
∴∠CPE=∠CDE.
∵四边形ABCD为菱形,∠ABC=120°,∴∠ADC=120°.
∴∠CDE=60°.∴∠CPE=60°.
∵PC=PE,∴△PCE是等边三角形.∴CE=PE.
∵PE=PA,∴CE=AP.
第5课时 正方形及其性质
基础训练
知识点1 正方形的定义
1.下面四个定义中不正确的是( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
2.下列说法错误的是( )
A.正方形是平行四边形 B.正方形是菱形
C.正方形是矩形 D.菱形和矩形都是正方形
3.已知,在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )21·cn·jy·com
A.∠D=90° B.AB=CD
C.AD=BC D.BC=CD
知识点2 正方形边的性质
4.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.四条边相等
C.对角线相等 D.对角线互相平分
5.(2016·广东)如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )【来源:21·世纪·教育·网】
A.B. 2 C.+1 D.2+1
6.如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为( )21·世纪*教育网
A.2 B.3
C. D.
7.(2016·毕节)如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )www-2-1-cnjy-com
A.3 B.4 C.5 D.6
知识点3 正方形角的性质
8.如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数
是 .?
9.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠AED的度数是____________?2-1-c-n-j-y
10.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC等于( )
A.45° B.55° C.60° D.75°
易错点 不能将两线段和转化为一条线段而致错
11.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .?
提升训练
考查角度1 利用正方形性质解边角问题
12.如图,在正方形ABCD的外侧作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE;
(2)求∠BEC的度数.
考查角度2 利用正方形性质判定图形形状
13.(2016·贵阳)如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE,CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
探究培优
拔尖角度1 利用三角形、正方形的性质探究两线段间的关系
14.如图①,在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 .?
(2)如图②,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并说明理由.21cnjy.com
(3)若△ADE和△DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.21教育网
拔尖角度2 利用正方形的性质探究改变条件时的结论情况(类比思想)
15.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F. www.21-cn-jy.com
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.21世纪教育网版权所有
参考答案
1.【答案】B 2.【答案】D 3.【答案】D 4.【答案】B
5.【答案】B
解:由正方形的性质和已知条件得出BC=CD=1,∠BCD=90°,CE=CF=,所以△CEF是等腰直角三角形.再利用勾股定理求出EF的长,即可得出正方形EFGH的周长.2·1·c·n·j·y
6.【答案】A
解:延长AB至点F',使BF'=DF,连接CF',EF,先证明Rt△CDF≌Rt△CBF',再证明△ECF≌△ECF',得出EF=EF',最后在Rt△AEF中,利用勾股定理、方程思想解决问题.21*cnjy*com
7.【答案】B
解:根据折叠的性质可得DH=EH,在Rt△CEH中,若设CH=x,则DH=EH=9-x,EC=3,可以根据勾股定理列出方程,从而得出CH的长.
8.【答案】90° 9.【答案】65° 10.【答案】C
11.【答案】
解:在AD上取一点M,使得AM=2,连接EM,交AC于点P,易得此时PF+PE的值最小,即EM的长为PF+PE的最小值.过点M作MN⊥BC于N,由题意可知EN=BN-BE=AM-BE=2-1=1,MN=4,所以EM===. 【来源:21cnj*y.co*m】
易错解:此类问题容易出错的地方是不能将两条线段的和转化为一条线段.
方法规律:正方形是特殊的平行四边形,由于正方形是轴对称图形,求线段和的最小值,往往要通过轴对称的方式将同侧两点转化为异侧两点,通过两点间线段最短求得两线段和的最小值.【出处:21教育名师】
12.(1)证明:∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°.
∵三角形ADE为等边三角形,
∴AE=AD=DE,∠EAD=∠EDA=60°.
∴∠BAE=∠CDE=150°.
∴△BAE≌△CDE.∴BE=CE.
(2)解:∵AB=AD,AD=AE,
∴AB=AE.
∴∠ABE=∠AEB.
又∵∠BAE=150°,
∴∠ABE=∠AEB=15°.
同理可得∠CED=15°,
∴∠BEC=60°-15°×2=30°.
13.(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°.
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF.
∴∠ABC-∠CBF=∠EBF-∠CBF.
∴∠ABF=∠CBE.
在△ABF和△CBE中,
有
∴△ABF≌△CBE(SAS).
(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°.
∴∠AFB=180°-∠BFE=135°.
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°.
∴∠CEF=∠CEB-∠FEB=135°-45°=90°.
∴△CEF是直角三角形.
14.解:(1)AF=BE;AF⊥BE
(2)结论成立.
理由:∵四边形ABCD是正方形,
∴BA=AD=DC,∠BAD=∠ADC=90°.
在△EAD和△FDC中,
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,即∠BAE=∠ADF.
在△BAE和△ADF中,
∴△BAE≌△ADF.
∴BE=AF,∠ABE=∠DAF.
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°.
∴AF⊥BE.
(3)结论都能成立.
15.(1)证明:方法一:∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP.
在△ADP和△CDP中,
∴△ADP≌△CDP.∴PA=PC.
∵PA=PE,∴PC=PE.
方法二:∵四边形ABCD是正方形,
∴直线BD是此正方形的一条对称轴,点A,C关于直线BD对称.
又∵P是BD上一点,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)解:∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠CDE=90°.
∴∠E+∠DFE=90°.
∵PA=PE,∴∠PAD=∠E.
又∵△ADP≌△CDP,
∴∠PAD=∠PCD.
∴∠PCD=∠E.
∵∠PFC=∠DFE,∴∠PCD+∠PFC=∠E+∠DFE=90°.
∴∠CPE=90°.
(3)解:CE=AP.理由:
易证△ADP≌△CDP,
∴PA=PC,∠PAD=∠PCD.
∵PA=PE,
∴PC=PE,∠PAE=∠PEA.
∴∠PEA=∠PCD.
∵∠EFC=∠CPE+∠PCD=∠CDE+∠PEA,
∴∠CPE=∠CDE.
∵四边形ABCD为菱形,∠ABC=120°,∴∠ADC=120°.
∴∠CDE=60°.∴∠CPE=60°.
∵PC=PE,∴△PCE是等边三角形.∴CE=PE.
∵PE=PA,∴CE=AP.
