18.2 .3 正方形的判定 同步练习
文档属性
| 名称 | 18.2 .3 正方形的判定 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 484.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:13:01 | ||
图片预览

文档简介
18.2 特殊的平行四边形
第6课时 正方形的判定
基础训练
知识点1 正方形面积的性质
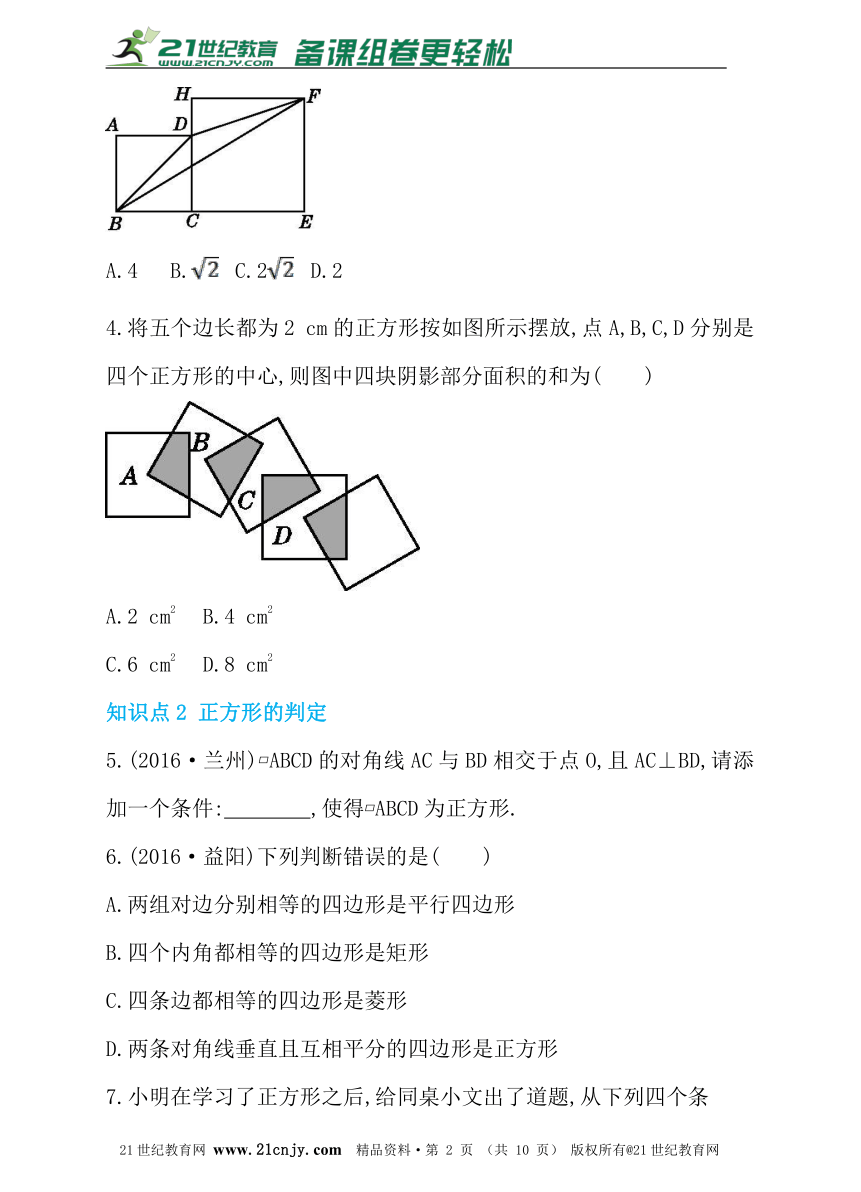
1.(2016·南京)如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为___________.21世纪教育网版权所有
2.如图,点E在正方形ABCD的对角线AC上,E为AC中点,直角三角形FEG的两条直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则阴影部分即四边形EMCN的面积为( )21cnjy.com
A.a2 B.a2 C.a2 D.a2
3.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )www.21-cn-jy.com
A.4 B. C.2 D.2
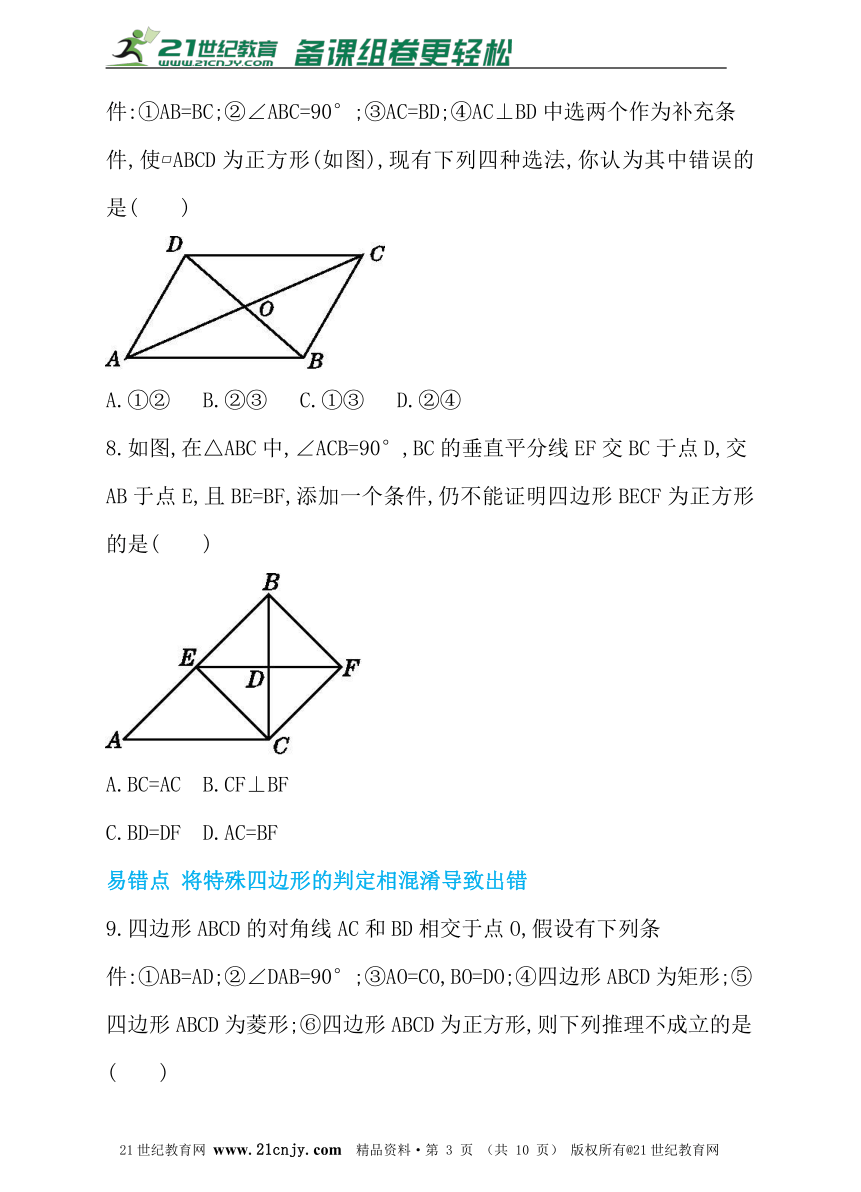
4.将五个边长都为2 cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2 B.4 cm2
C.6 cm2 D.8 cm2
知识点2 正方形的判定
5.(2016·兰州)?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得?ABCD为正方形.【来源:21·世纪·教育·网】
6.(2016·益阳)下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
7.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条
件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条
件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
8.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交
AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
易错点 将特殊四边形的判定相混淆导致出错
9.四边形ABCD的对角线AC和BD相交于点O,假设有下列条
件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④四边形ABCD为矩形;⑤
四边形ABCD为菱形;⑥四边形ABCD为正方形,则下列推理不成立的是
( )
A.①④?⑥ B.①③?⑤
C.①②?⑥ D.②③?④
提升训练
考查角度1 利用矩形为基础判定正方形
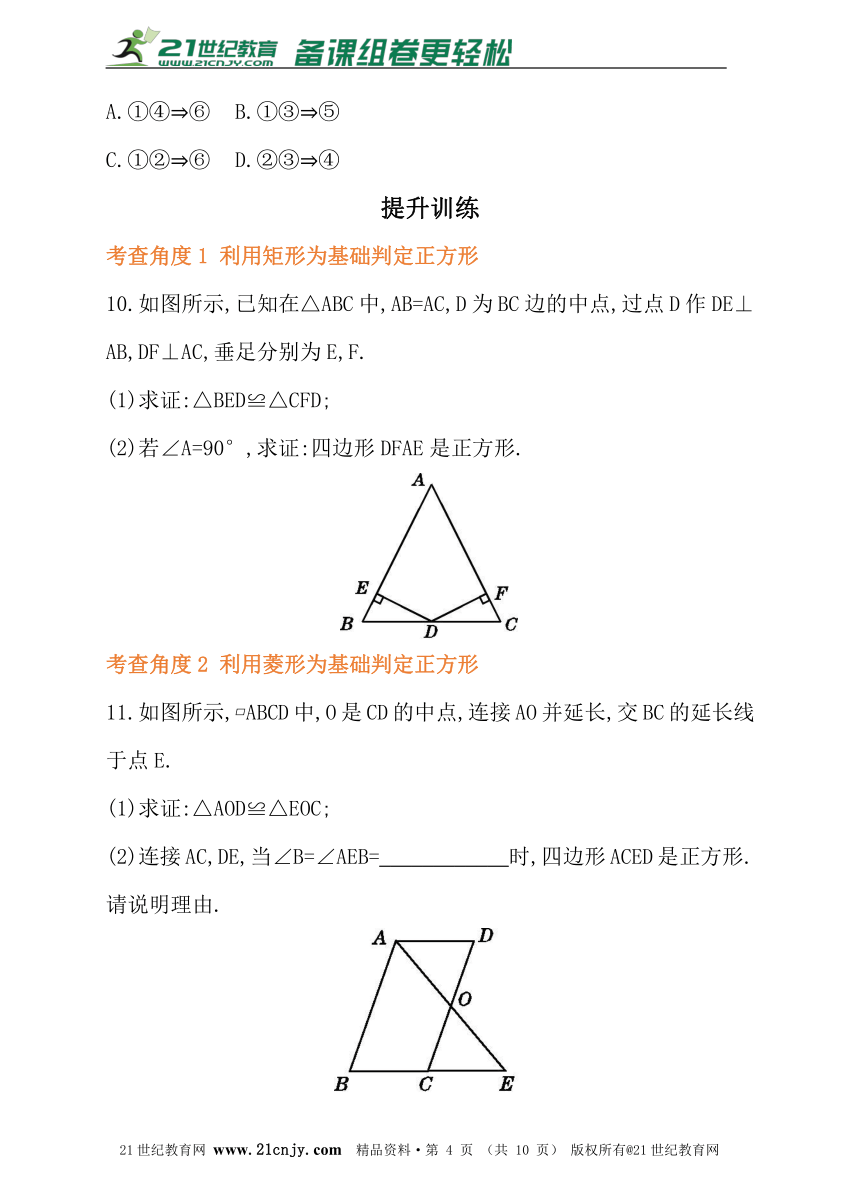
10.如图所示,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.21·cn·jy·com
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
考查角度2 利用菱形为基础判定正方形
11.如图所示,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=____________时,四边形ACED是正方形.请说明理由.?21·世纪*教育网
探究培优
拔尖角度1 利用特殊四边形的判定说明四边形的形状
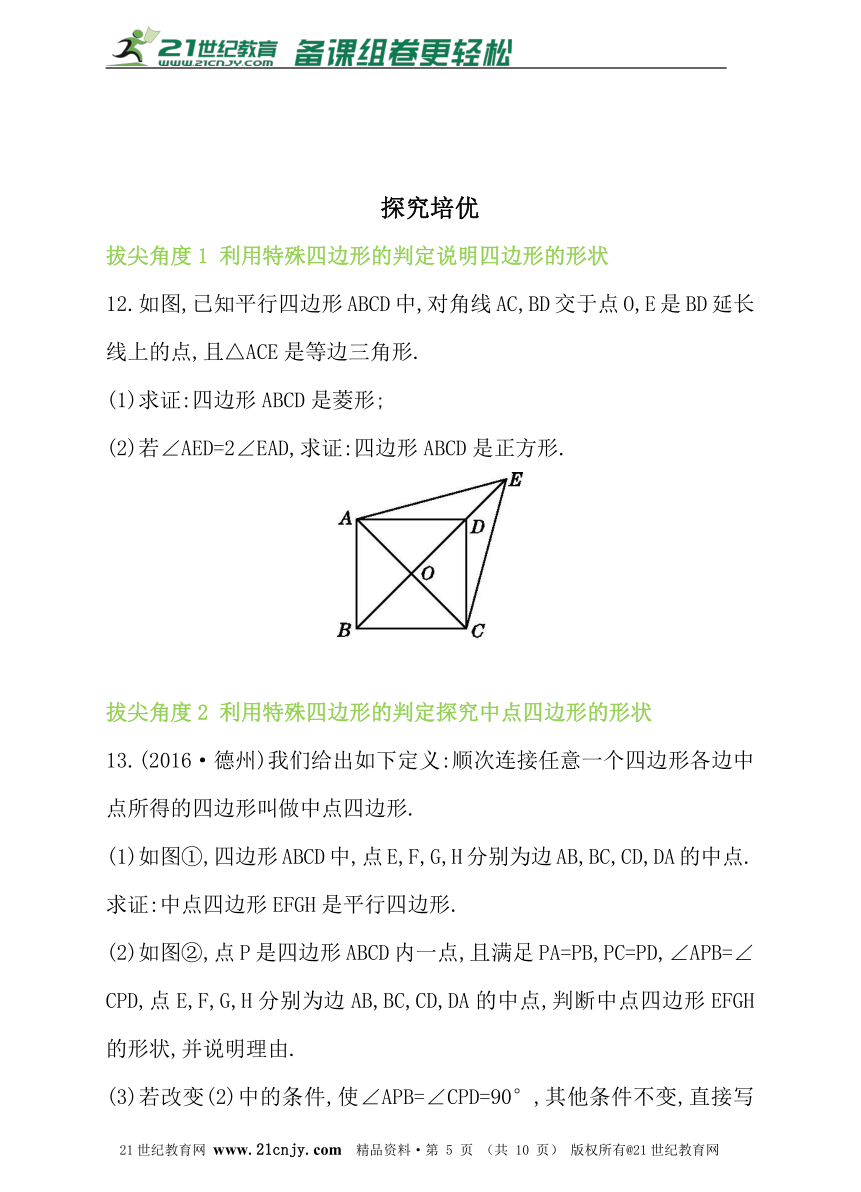
12.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.www-2-1-cnjy-com
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
拔尖角度2 利用特殊四边形的判定探究中点四边形的形状
13.(2016·德州)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2-1-c-n-j-y
(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形.
(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,判断中点四边形EFGH的形状,并说明理由.2·1·c·n·j·y
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)21*cnjy*com
参考答案
1.【答案】13 cm
解:连接AC,BD.因为正方形AECF的面积为50 cm2,
所以AC===10(cm).
因为菱形ABCD的面积为120 cm2,
所以BD==24(cm).
所以菱形的边长为=13(cm).
2.【答案】B
3.【答案】D
解:如图,连接CF,则∠DBC=∠FCE=45°,∴CF∥BD.∴△BDF与△BDC
同底等高.∴S△BDF=S△BCD=×2×2=2.故选D.
4.【答案】B
5.【答案】∠BAD=90°(答案不唯一)
6.【答案】D
解:两条对角线垂直且互相平分的四边形只能判定为菱形,只有两条对角线垂直、互相平分且相等的四边形才为正方形.21教育网
7.【答案】B 8.【答案】D 9.【答案】C
10.证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,∴BD=CD.
∴△BED≌△CFD;
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵∠A=90°,
∴四边形DFAE为矩形.
∵△BED≌△CFD,∴DE=DF.
∴四边形DFAE为正方形.
11.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
又∵O是CD的中点,∴OD=OC,
∴△AOD≌△EOC.
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.理由如下:
如图,∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴?ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.∴菱形ACED是正方形.
12.证明:(1)∵四边形ABCD为平行四边形,
∴AO=OC.
∵△ACE为等边三角形.
∴OE⊥AC,∴四边形ABCD为菱形.
(2)∵△ACE是等边三角形,
∴∠AED=×60°=30°.
∴∠EAD=15°,
∴∠DAC=60°-15°=45°.
∵AO=CO,OE⊥AC,
∴AD=DC,∴∠ADC=90°.
∴四边形ABCD为正方形.
13.(1)证明:如图①,连接BD.
∵点E,H分别为边AB,DA的中点,
∴EH∥BD,EH=BD.
∵点F,G分别为边BC,CD的中点,
∴FG∥BD,FG=BD.
∴EH∥FG,EH=FG.
∴中点四边形EFGH是平行四边形.
(2)解:四边形EFGH是菱形.理由如下:
如图②,连接AC,BD.
∵∠APB=∠CPD,
∴∠APB+∠APD=∠CPD+∠APD,
即∠APC=∠BPD.
在△APC和△BPD中,
∴△APC≌△BPD(SAS).
∴AC=BD.
∵点E,F,G分别为边AB,BC,CD的中点,
∴EF=AC,FG=BD.
∴EF=FG.
又由(1)中结论知四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
(3)解:四边形EFGH是正方形.
第6课时 正方形的判定
基础训练
知识点1 正方形面积的性质
1.(2016·南京)如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为___________.21世纪教育网版权所有
2.如图,点E在正方形ABCD的对角线AC上,E为AC中点,直角三角形FEG的两条直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则阴影部分即四边形EMCN的面积为( )21cnjy.com
A.a2 B.a2 C.a2 D.a2
3.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )www.21-cn-jy.com
A.4 B. C.2 D.2
4.将五个边长都为2 cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2 B.4 cm2
C.6 cm2 D.8 cm2
知识点2 正方形的判定
5.(2016·兰州)?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得?ABCD为正方形.【来源:21·世纪·教育·网】
6.(2016·益阳)下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
7.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条
件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条
件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
8.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交
AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
易错点 将特殊四边形的判定相混淆导致出错
9.四边形ABCD的对角线AC和BD相交于点O,假设有下列条
件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④四边形ABCD为矩形;⑤
四边形ABCD为菱形;⑥四边形ABCD为正方形,则下列推理不成立的是
( )
A.①④?⑥ B.①③?⑤
C.①②?⑥ D.②③?④
提升训练
考查角度1 利用矩形为基础判定正方形
10.如图所示,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.21·cn·jy·com
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
考查角度2 利用菱形为基础判定正方形
11.如图所示,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=____________时,四边形ACED是正方形.请说明理由.?21·世纪*教育网
探究培优
拔尖角度1 利用特殊四边形的判定说明四边形的形状
12.如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.www-2-1-cnjy-com
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
拔尖角度2 利用特殊四边形的判定探究中点四边形的形状
13.(2016·德州)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2-1-c-n-j-y
(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形.
(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,判断中点四边形EFGH的形状,并说明理由.2·1·c·n·j·y
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)21*cnjy*com
参考答案
1.【答案】13 cm
解:连接AC,BD.因为正方形AECF的面积为50 cm2,
所以AC===10(cm).
因为菱形ABCD的面积为120 cm2,
所以BD==24(cm).
所以菱形的边长为=13(cm).
2.【答案】B
3.【答案】D
解:如图,连接CF,则∠DBC=∠FCE=45°,∴CF∥BD.∴△BDF与△BDC
同底等高.∴S△BDF=S△BCD=×2×2=2.故选D.
4.【答案】B
5.【答案】∠BAD=90°(答案不唯一)
6.【答案】D
解:两条对角线垂直且互相平分的四边形只能判定为菱形,只有两条对角线垂直、互相平分且相等的四边形才为正方形.21教育网
7.【答案】B 8.【答案】D 9.【答案】C
10.证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC的中点,∴BD=CD.
∴△BED≌△CFD;
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵∠A=90°,
∴四边形DFAE为矩形.
∵△BED≌△CFD,∴DE=DF.
∴四边形DFAE为正方形.
11.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
又∵O是CD的中点,∴OD=OC,
∴△AOD≌△EOC.
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.理由如下:
如图,∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴?ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.∴菱形ACED是正方形.
12.证明:(1)∵四边形ABCD为平行四边形,
∴AO=OC.
∵△ACE为等边三角形.
∴OE⊥AC,∴四边形ABCD为菱形.
(2)∵△ACE是等边三角形,
∴∠AED=×60°=30°.
∴∠EAD=15°,
∴∠DAC=60°-15°=45°.
∵AO=CO,OE⊥AC,
∴AD=DC,∴∠ADC=90°.
∴四边形ABCD为正方形.
13.(1)证明:如图①,连接BD.
∵点E,H分别为边AB,DA的中点,
∴EH∥BD,EH=BD.
∵点F,G分别为边BC,CD的中点,
∴FG∥BD,FG=BD.
∴EH∥FG,EH=FG.
∴中点四边形EFGH是平行四边形.
(2)解:四边形EFGH是菱形.理由如下:
如图②,连接AC,BD.
∵∠APB=∠CPD,
∴∠APB+∠APD=∠CPD+∠APD,
即∠APC=∠BPD.
在△APC和△BPD中,
∴△APC≌△BPD(SAS).
∴AC=BD.
∵点E,F,G分别为边AB,BC,CD的中点,
∴EF=AC,FG=BD.
∴EF=FG.
又由(1)中结论知四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
(3)解:四边形EFGH是正方形.
