27.2.1相似三角形的判定3 课件
图片预览




文档简介
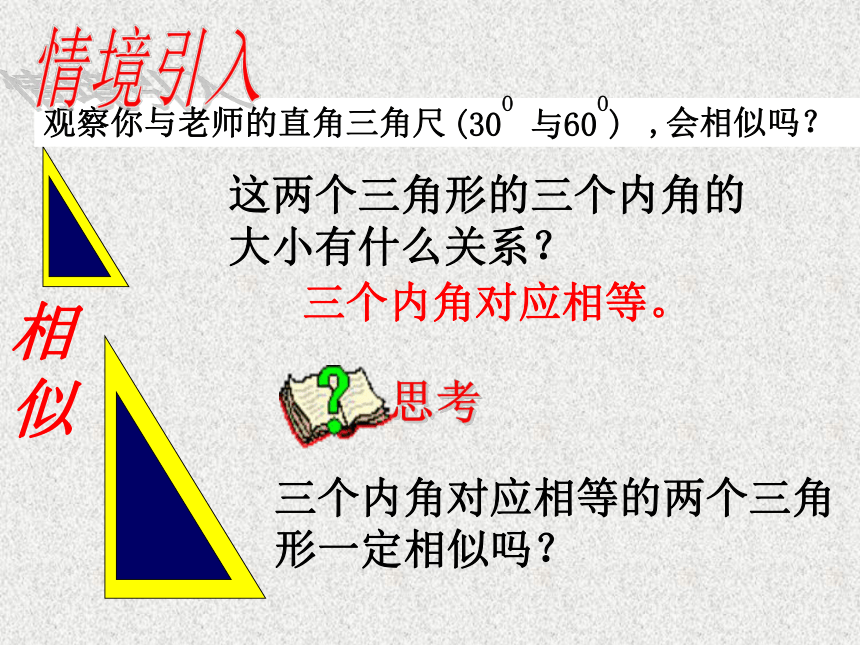
课件17张PPT。27.2.1.3相似三角形的判定3知识回顾相似三角形的识别方法有那些?方法1:通过定义方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角。这两个三角形的三个内角的大小有什么关系?三个内角对应相等的两个三角形一定相似吗?三个内角对应相等。观察你与老师的直角三角尺 ,会相似吗?(30O 与60O) 相
似情境引入 画△ ,使三个角分别为60°,45°, 75° 。①同桌分别量出两个三角形三边的长度;
②同桌这两个三角形相似吗? 即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
一定需三个角吗? 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.相似三角形的识别方法:思 考
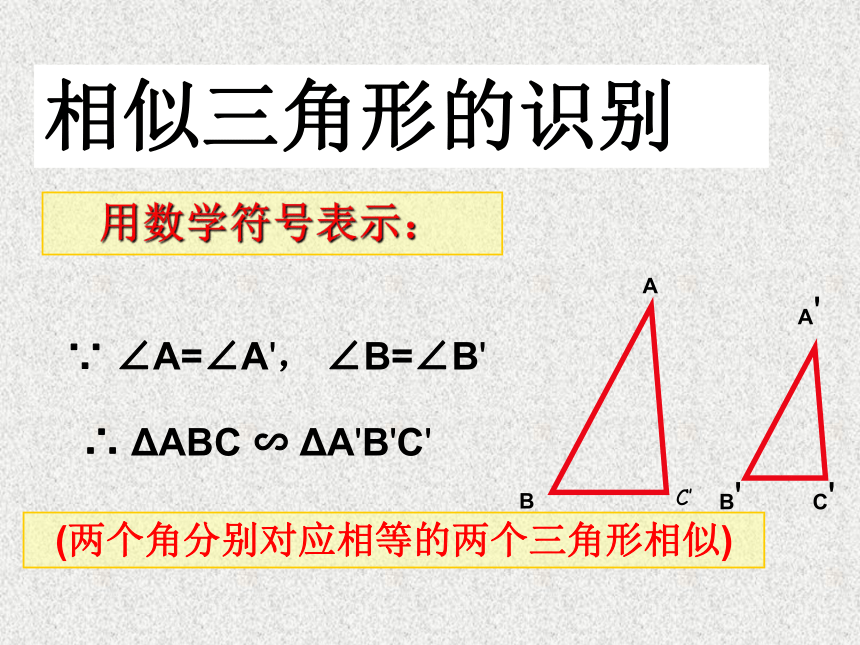
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似? 相似不一定相似C'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(两个角分别对应相等的两个三角形相似)C’新知探究例2 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC
上一点,AE=5,ED⊥AB,垂足为D。求AD的长,解:∵ ED⊥AB
∴∠EDB=90°.
又∠C=90°, ∠A= ∠A
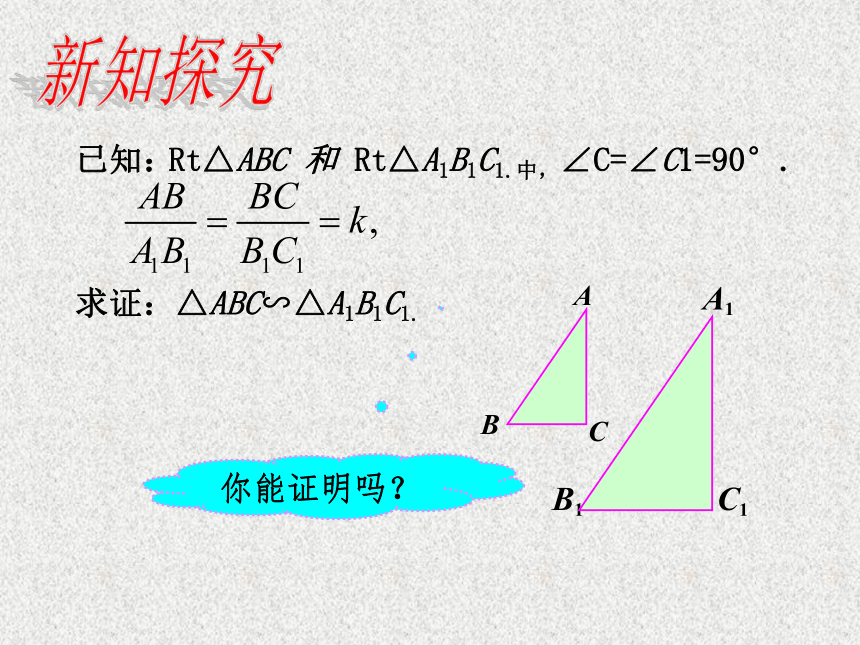
∴△AED∽△ABC新知探究已知:△ABC∽△A1B1C1.求证:Rt△ABC 和 Rt△A1B1C1.中,∠C=∠C1=90°.
你能证明吗? 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。判定三角形相似的定理之HL△ABC∽△A1B1C1.在Rt△ABC 和 Rt△A1B1C1中符号语言:知识梳理本节课学习了什么知识? 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。课堂小结 相似图形三角形的判定方法: 通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例(三边对应成比例,三角相等)(SSS)(AA)(SAS)(HL)例1.弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.ABCDPO证明:连接AC、BD.∵∠A、∠D都是CB所对的圆周角,⌒∴ ∠A=∠D.同理: ∠C=∠B.∴△PAC∽△PDB.即PA·PB=PC·PD.新知应用解: ∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.例2. 已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB. 新知应用随堂练习1.找出图中所有的相似三角形△ACD ∽ △ CBD∽ △ ABC你能写出对应边的比例式吗?CADB2、填一填
(1)如图3,点D在AB上,当∠ =∠ 时, △ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
DBACD或∠ ACB或∠ ADCDBCA
(1)所有的等腰直角三角形都相似。
(2)有一个角是100 °的两个等腰三角形都相似。
(3)有一个角是70 °的两个等腰三角形都相似。
(4)若两个三角形相似比为1,则它们必全等。
(5)相似的两个三角形一定大小不等。4、 判断下列说法是否正确?并说明理由。在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条? 我们来试一试…
似情境引入 画△ ,使三个角分别为60°,45°, 75° 。①同桌分别量出两个三角形三边的长度;
②同桌这两个三角形相似吗? 即:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
一定需三个角吗? 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.相似三角形的识别方法:思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似? 相似不一定相似C'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(两个角分别对应相等的两个三角形相似)C’新知探究例2 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC
上一点,AE=5,ED⊥AB,垂足为D。求AD的长,解:∵ ED⊥AB
∴∠EDB=90°.
又∠C=90°, ∠A= ∠A
∴△AED∽△ABC新知探究已知:△ABC∽△A1B1C1.求证:Rt△ABC 和 Rt△A1B1C1.中,∠C=∠C1=90°.
你能证明吗? 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。判定三角形相似的定理之HL△ABC∽△A1B1C1.在Rt△ABC 和 Rt△A1B1C1中符号语言:知识梳理本节课学习了什么知识? 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。课堂小结 相似图形三角形的判定方法: 通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例(三边对应成比例,三角相等)(SSS)(AA)(SAS)(HL)例1.弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.ABCDPO证明:连接AC、BD.∵∠A、∠D都是CB所对的圆周角,⌒∴ ∠A=∠D.同理: ∠C=∠B.∴△PAC∽△PDB.即PA·PB=PC·PD.新知应用解: ∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.例2. 已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB. 新知应用随堂练习1.找出图中所有的相似三角形△ACD ∽ △ CBD∽ △ ABC你能写出对应边的比例式吗?CADB2、填一填
(1)如图3,点D在AB上,当∠ =∠ 时, △ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
DBACD或∠ ACB或∠ ADCDBCA
(1)所有的等腰直角三角形都相似。
(2)有一个角是100 °的两个等腰三角形都相似。
(3)有一个角是70 °的两个等腰三角形都相似。
(4)若两个三角形相似比为1,则它们必全等。
(5)相似的两个三角形一定大小不等。4、 判断下列说法是否正确?并说明理由。在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条? 我们来试一试…
