19.1 函数 第2课时 函数 同步练习
文档属性
| 名称 | 19.1 函数 第2课时 函数 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-14 21:55:03 | ||
图片预览



文档简介
19.1 函数
第2课时 函数
基础训练
知识点1函数的定义
1.下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:菱形的周长,x:这个菱形的边长
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数
2.下列关系式中,y不是x的函数的是( )
A.y=±(x>0) B.y=x2
C.y=-(x>0) D.y=()2(x>0)
3.下列关于变量x,y的关系式:①3x-2y=5;②y=|x+1|;③2x-y2=10,其中表示y是x的函数关系的是( )21教育网
A.①②③ B.①②
C.①③ D.②③
4.(2016·南宁)下列各曲线中表示y是x的函数的是( )
5.下列说法正确的是( )
A.变量x,y满足y2=x,则y是x的函数
B.变量x,y满足x+3y=1,则y是x的函数
C.变量x,y满足|y|=x,则y是x的函数
D.在V=πr3中,是常量,r是自变量,V是r的函数
知识点2自变量的取值范围
6.(2016·无锡)函数y=中自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≤2 D.x≠2
7.如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
A.y=x+2 B.y=x2+2
C.y= D.y=
8.(2016·黄冈)在函数y=中,自变量x的取值范围是( )
A.x>0 B.x≥-4
C.x≥-4且x≠0 D.x>-4且x≠0
9.在函数y=+(x-2)0中,自变量x的取值范围是___________.?
知识点3函数值
10.下列关系式中,当自变量x=-1时,函数值y=6的是( )
A.y=3x+3 B.y=-3x+3
C.y=3x-3 D.y=-3x-3
11.已知函数y=当x=2时,函数值y为( )
A.5 B.6 C.7 D.8
12.若函数y=则当函数值y=8时,自变量x的值是( )
A.± B.4
C.±或4 D.4或-
13.如果两个变量x,y之间的函数关系如图所示,则函数值y的取值范围是( )
A.-3≤y≤3 B.0≤y≤2 C.1≤y≤3 D.0≤y≤3
易错点 用函数关系式表示实际问题时弄错自变量的取值范围
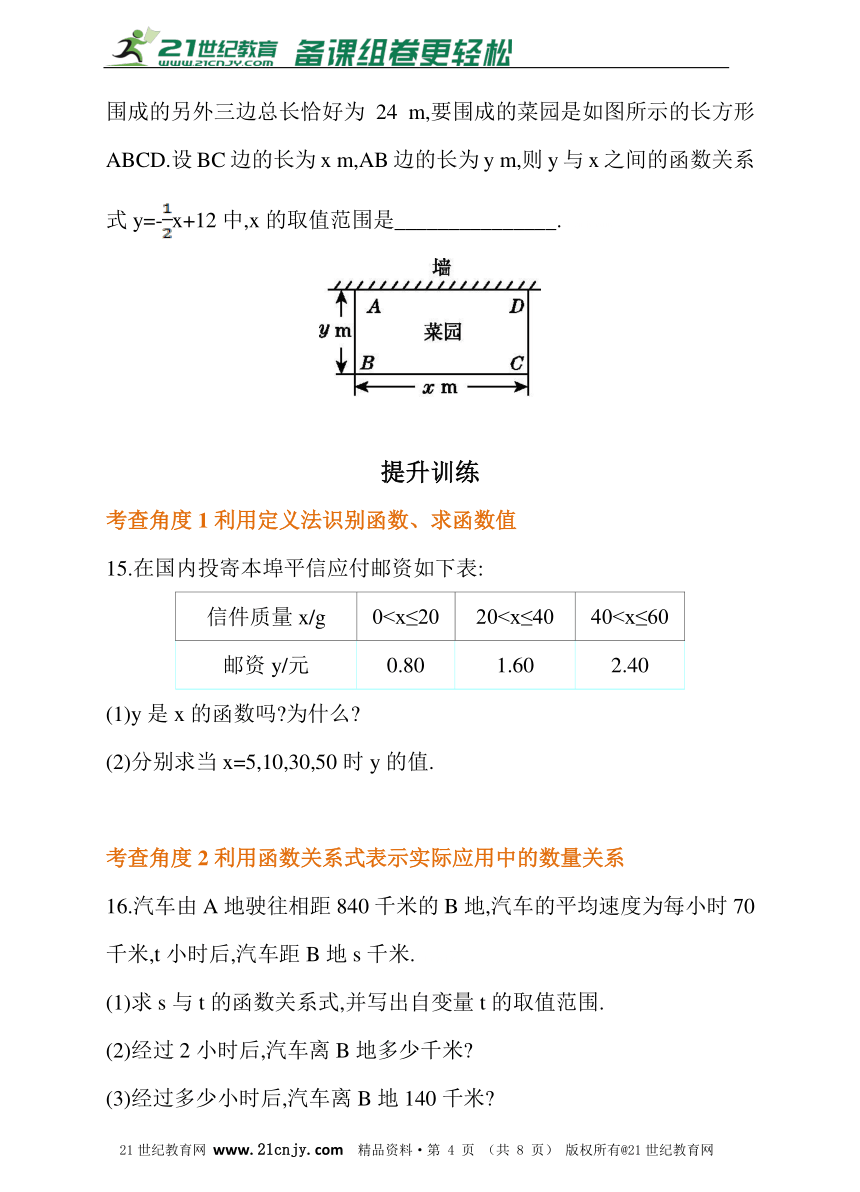
14.李大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长恰好为24 m,要围成的菜园是如图所示的长方形ABCD.设BC边的长为x m,AB边的长为y m,则y与x之间的函数关系式y=-x+12中,x的取值范围是_______________.21·cn·jy·com
提升训练
考查角度1利用定义法识别函数、求函数值
15.在国内投寄本埠平信应付邮资如下表:
信件质量x/g
02040邮资y/元
0.80
1.60
2.40
(1)y是x的函数吗?为什么?
(2)分别求当x=5,10,30,50时y的值.
考查角度2利用函数关系式表示实际应用中的数量关系
16.汽车由A地驶往相距840千米的B地,汽车的平均速度为每小时70千米,t小时后,汽车距B地s千米.2·1·c·n·j·y
(1)求s与t的函数关系式,并写出自变量t的取值范围.
(2)经过2小时后,汽车离B地多少千米?
(3)经过多少小时后,汽车离B地140千米?
探究培优
拔尖角度1利用图表信息求函数关系式及函数值(从特殊到一般的思想)
17.如图,结合表格中的数据回答问题:
梯形的个数
1
2
3
4
5
…
图形的周长
5
8
11
14
17
…
(1)设图形的周长为l,梯形的个数为n,试写出l与n的函数关系式;
(2)求n=11时,图形的周长;
(3)求l=302时,梯形的个数.
拔尖角度2利用函数关系式表示几何中的数量关系
18.如图,在矩形ABCD中,AB=4,BC=7,点P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点R,交AD于点Q(点Q与点D不重合),且∠RPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围. 21cnjy.com
参考答案
1.【答案】D 2. 【答案】A
3. 【答案】B
解:只要保证x对应的y只有一个值即可,选B①可以化成一次函数,②是关于x的二次函数③是关于y的二次函数,比如你取x=1的时候,y有两个值www.21-cn-jy.com
4. 【答案】D
解:根据函数的意义可知,对于自变量x的任何值,y都有唯一的值与之相对应,只有D才满足这一条件.故选D.【来源:21·世纪·教育·网】
5. 【答案】B 6. 【答案】B
7. 【答案】C
解:,x﹣2≥0,即x≥2,正确,故选C.
8. 【答案】C
解:由题意得解得x≥-4且x≠0.
9. 【答案】x>-2且x≠2
10. 【答案】B 11. 【答案】A
12. 【答案】D
13. 【答案】D
解:从题图可以看出y的最大值是3,最小值是0,所以0≤y≤3,选D.
14. 【答案】0解:本题易错之处在于只考虑x>0,而忽视y>0.给出x的取值范围为x>0.
15.解:(1)y是x的函数,理由:当x取定一个值时,y都有唯一确定的值与其对应.
(2)当x=5时,y=0.80;当x=10时,y=0.80;当x=30时,y=1.60;当x=50时,y=2.40.21世纪教育网版权所有
16.解:(1)s=840-70t(0≤t≤12).
(2)当t=2时,s=840-70×2=700(千米).
(3)当s=140时,140=840-70t,t=10(小时).
17.解:(1)l与n的函数关系式为l=3n+2(n为正整数).
(2)把n=11代入l=3n+2,得l=3×11+2=35.
所以n=11时,图形的周长为35.
(3)把l=302代入l=3n+2,
得302=3n+2,所以n=100,
即l=302时,梯形的个数为100.
18.解:如图,过点D作DP'∥PQ,交BC于点P',
则∠DP'C=∠RPC=45°,
∴P'C=CD=4,∴BP'=3.∴BP<3.
∵BP=x,则PC=7-x.
在Rt△PCR中,∠C=90°,
∠RPC=45°,
∴CR=PC=7-x.
∴QD=RD=CR-CD
=7-x-4
=3-x,
∴AQ=AD-QD
=7-(3-x)
=4+x.
∴y=(BP+AQ)·AB
=(x+4+x)×4
=4x+8(0
第2课时 函数
基础训练
知识点1函数的定义
1.下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:菱形的周长,x:这个菱形的边长
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数
2.下列关系式中,y不是x的函数的是( )
A.y=±(x>0) B.y=x2
C.y=-(x>0) D.y=()2(x>0)
3.下列关于变量x,y的关系式:①3x-2y=5;②y=|x+1|;③2x-y2=10,其中表示y是x的函数关系的是( )21教育网
A.①②③ B.①②
C.①③ D.②③
4.(2016·南宁)下列各曲线中表示y是x的函数的是( )
5.下列说法正确的是( )
A.变量x,y满足y2=x,则y是x的函数
B.变量x,y满足x+3y=1,则y是x的函数
C.变量x,y满足|y|=x,则y是x的函数
D.在V=πr3中,是常量,r是自变量,V是r的函数
知识点2自变量的取值范围
6.(2016·无锡)函数y=中自变量x的取值范围是( )
A.x>2 B.x≥2 C.x≤2 D.x≠2
7.如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
A.y=x+2 B.y=x2+2
C.y= D.y=
8.(2016·黄冈)在函数y=中,自变量x的取值范围是( )
A.x>0 B.x≥-4
C.x≥-4且x≠0 D.x>-4且x≠0
9.在函数y=+(x-2)0中,自变量x的取值范围是___________.?
知识点3函数值
10.下列关系式中,当自变量x=-1时,函数值y=6的是( )
A.y=3x+3 B.y=-3x+3
C.y=3x-3 D.y=-3x-3
11.已知函数y=当x=2时,函数值y为( )
A.5 B.6 C.7 D.8
12.若函数y=则当函数值y=8时,自变量x的值是( )
A.± B.4
C.±或4 D.4或-
13.如果两个变量x,y之间的函数关系如图所示,则函数值y的取值范围是( )
A.-3≤y≤3 B.0≤y≤2 C.1≤y≤3 D.0≤y≤3
易错点 用函数关系式表示实际问题时弄错自变量的取值范围
14.李大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长恰好为24 m,要围成的菜园是如图所示的长方形ABCD.设BC边的长为x m,AB边的长为y m,则y与x之间的函数关系式y=-x+12中,x的取值范围是_______________.21·cn·jy·com
提升训练
考查角度1利用定义法识别函数、求函数值
15.在国内投寄本埠平信应付邮资如下表:
信件质量x/g
0
0.80
1.60
2.40
(1)y是x的函数吗?为什么?
(2)分别求当x=5,10,30,50时y的值.
考查角度2利用函数关系式表示实际应用中的数量关系
16.汽车由A地驶往相距840千米的B地,汽车的平均速度为每小时70千米,t小时后,汽车距B地s千米.2·1·c·n·j·y
(1)求s与t的函数关系式,并写出自变量t的取值范围.
(2)经过2小时后,汽车离B地多少千米?
(3)经过多少小时后,汽车离B地140千米?
探究培优
拔尖角度1利用图表信息求函数关系式及函数值(从特殊到一般的思想)
17.如图,结合表格中的数据回答问题:
梯形的个数
1
2
3
4
5
…
图形的周长
5
8
11
14
17
…
(1)设图形的周长为l,梯形的个数为n,试写出l与n的函数关系式;
(2)求n=11时,图形的周长;
(3)求l=302时,梯形的个数.
拔尖角度2利用函数关系式表示几何中的数量关系
18.如图,在矩形ABCD中,AB=4,BC=7,点P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点R,交AD于点Q(点Q与点D不重合),且∠RPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围. 21cnjy.com
参考答案
1.【答案】D 2. 【答案】A
3. 【答案】B
解:只要保证x对应的y只有一个值即可,选B①可以化成一次函数,②是关于x的二次函数③是关于y的二次函数,比如你取x=1的时候,y有两个值www.21-cn-jy.com
4. 【答案】D
解:根据函数的意义可知,对于自变量x的任何值,y都有唯一的值与之相对应,只有D才满足这一条件.故选D.【来源:21·世纪·教育·网】
5. 【答案】B 6. 【答案】B
7. 【答案】C
解:,x﹣2≥0,即x≥2,正确,故选C.
8. 【答案】C
解:由题意得解得x≥-4且x≠0.
9. 【答案】x>-2且x≠2
10. 【答案】B 11. 【答案】A
12. 【答案】D
13. 【答案】D
解:从题图可以看出y的最大值是3,最小值是0,所以0≤y≤3,选D.
14. 【答案】0
15.解:(1)y是x的函数,理由:当x取定一个值时,y都有唯一确定的值与其对应.
(2)当x=5时,y=0.80;当x=10时,y=0.80;当x=30时,y=1.60;当x=50时,y=2.40.21世纪教育网版权所有
16.解:(1)s=840-70t(0≤t≤12).
(2)当t=2时,s=840-70×2=700(千米).
(3)当s=140时,140=840-70t,t=10(小时).
17.解:(1)l与n的函数关系式为l=3n+2(n为正整数).
(2)把n=11代入l=3n+2,得l=3×11+2=35.
所以n=11时,图形的周长为35.
(3)把l=302代入l=3n+2,
得302=3n+2,所以n=100,
即l=302时,梯形的个数为100.
18.解:如图,过点D作DP'∥PQ,交BC于点P',
则∠DP'C=∠RPC=45°,
∴P'C=CD=4,∴BP'=3.∴BP<3.
∵BP=x,则PC=7-x.
在Rt△PCR中,∠C=90°,
∠RPC=45°,
∴CR=PC=7-x.
∴QD=RD=CR-CD
=7-x-4
=3-x,
∴AQ=AD-QD
=7-(3-x)
=4+x.
∴y=(BP+AQ)·AB
=(x+4+x)×4
=4x+8(0
