19.1 函数 第3课时 函数的图象 同步练习
文档属性
| 名称 | 19.1 函数 第3课时 函数的图象 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 571.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-14 21:58:45 | ||
图片预览




文档简介
19.1 函数
第3课时 函数的图象
基础训练
知识点1函数的图象
1.下列图象不能表示y是x的函数的是( )
2.下列四个函数图象中,当x>0时,y随x的增大而减小的是( )
3.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )21·cn·jy·com
A.凌晨4时气温最低为-3 ℃
B.14时气温最高为8 ℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
4.甲、乙两人在操场上赛跑,他们赛跑的路程s(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )2·1·c·n·j·y
A.甲、乙两人进行1 000米赛跑
B.甲先慢后快,乙先快后慢
C.比赛到2分钟时,甲、乙两人跑过的路程相等
D.甲先到达终点
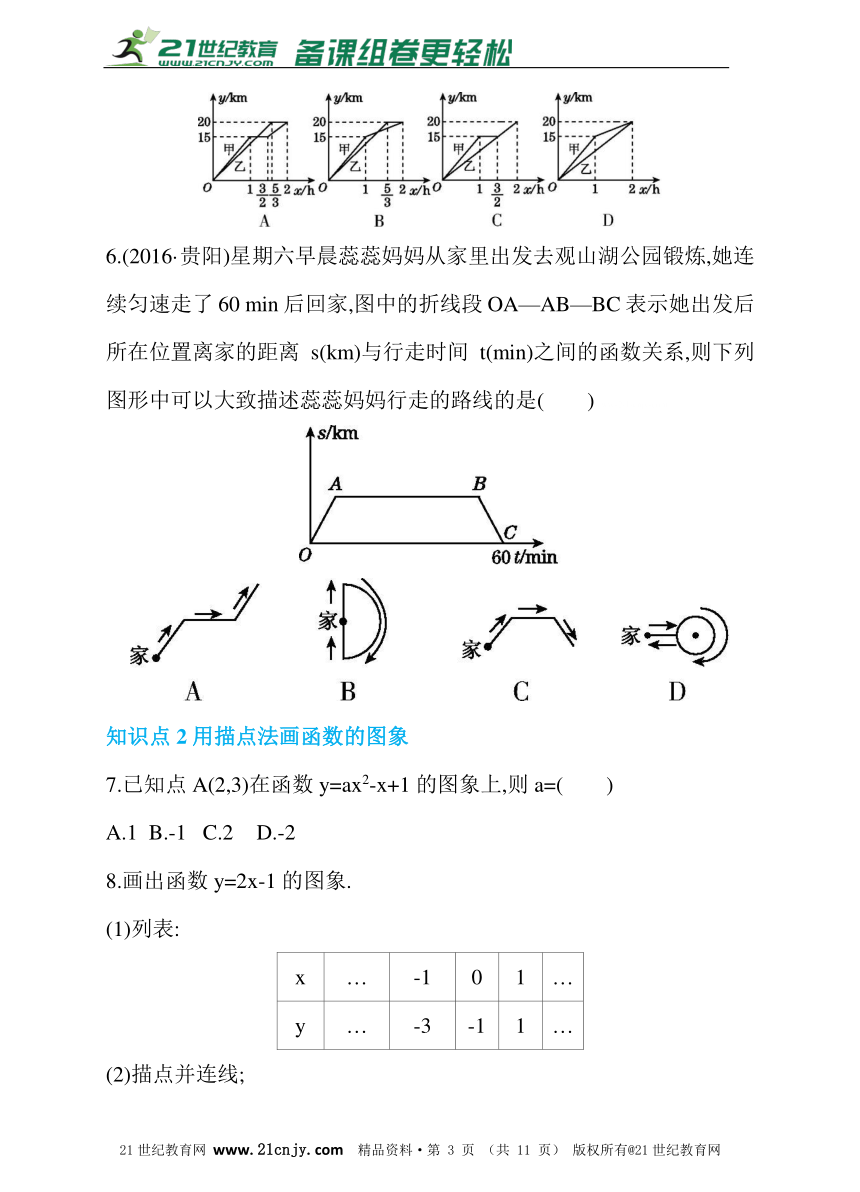
5.(2016·安徽)一段笔直的公路AC长20 km,途中有一处休息点B,AB长15 km,甲、乙两名长跑爱好者同时从点A出发,甲以15 km/h的速度匀速跑至点B,原地休息0.5 h后,再以10 km/h的速度匀速跑至终点C;乙以12 km/h的速度匀速跑至终点C,之后休息.下列选项中,能正确反映甲、乙两人出发后2 h内的运动路程y(km)与时间x(h)之间的函数关系的图象是( )21·世纪*教育网
6.(2016·贵阳)星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续匀速走了60 min后回家,图中的折线段OA—AB—BC表示她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线的是( )www-2-1-cnjy-com
知识点2用描点法画函数的图象
7.已知点A(2,3)在函数y=ax2-x+1的图象上,则a=( )
A.1 B.-1 C.2 D.-2
8.画出函数y=2x-1的图象.
(1)列表:
x
…
-1
0
1
…
y
…
-3
-1
1
…
(2)描点并连线;
(3)判断点A(-3,-5),B(2,-3),C(3,5)是否在函数y=2x-1的图象上;
(4)若点P(m,9)在函数y=2x-1的图象上,求出m的值.
易错点 画函数图象时易忽视自变量的取值范围导致出错
9. 某蜡烛原长20 cm,点燃后每小时燃烧5 cm,求剩余的蜡烛长度y(cm)与点燃的时间x(h)之间的函数解析式,并画出函数的图象.
提升训练
考查角度1利用描点法画函数的图象(描点法)
10.(1)画出函数y=x2的图象;
(2)画出函数y=x+1的图象;
(3)试判断点(-3,-2)是否在上述函数图象上.
考查角度2利用图象与情景间的关系互化
11.在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境a,b所对应的函数图象分别为________;(填写序号)?
(2)请你为剩下的函数图象写出一个适合的情境.
探究培优
拔尖角度1利用图象反映的信息说明其数学意义
12.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少?
(3)当y=0,4时,x的值分别是多少?
(4)当x取何值时,y的值最大?当x取何值时,y的值最小?
(5)当x的值在什么范围内时,y随x的增大而增大?当x的值在什么范围内时,y随x的增大而减小?
拔尖角度2利用图象反映的信息说明其实际意义
13.某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象.根据图象信息解答下列问题:2-1-c-n-j-y
(1)求张强返回时的速度.
(2)妈妈比按原速返回提前多少分到家?
(3)请直接写出张强与妈妈何时相距1 000米.
参考答案
1.【答案】C
2.【答案】B
3.【答案】C
解:A.∵由图象可知,在凌晨4时函数图象在最低点,∴凌晨4时气温最低为-3 ℃,故本选项正确;B.∵由图象可知,在14时函数图象在最高点,∴14时气温最高为8 ℃,故本选项正确;C.∵由图象可知,从4时至14时,气温随时间增长而上升,不是从0时,故本选项错误;D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.故选C.
4.【答案】C
解:观察函数图象可知:甲、乙两人进行1 000米赛跑;甲在前2.5分钟内,比乙慢,而在后面的时间内比乙快;甲跑完全程用时3.25分钟,乙跑完全程用时4分钟,所以甲先到达终点;比赛到2分钟时,甲跑的路程是500米,乙跑的路程是600米,两人跑过的路程不相等,综上可知选项A,B,D正确,选项C错误.21*cnjy*com
5.【答案】A
6.【答案】B
解:根据给定s关于t的函数图象,分析AB段可得出该段时间蕊蕊妈妈绕以家为圆心的圆弧进行运动,由此即可得出结论.21教育网
7.【答案】A
8.解:(2)如图.
(3)当x=-3时,y=2×(-3)-1=-7≠-5;当x=2时,y=2×2-1=3≠-3;当x=3时,y=2×3-1=5.∴点A,B不在函数y=2x-1的图象上,点C在其图象上.
(4)∵点P(m,9)在函数y=2x-1的图象上,∴2m-1=9,解得m=5.
9.解:根据题意得
y=20-5x(0≤x≤4).
函数图象如图.
10.分析:(1)用描点法(即列表、描点、连线的方法)画出该函数的图象即可.因为自变量x的取值范围为全体实数,所以在列表时可在x=0的两侧对称地取x的值,然后计算出相应的y的值;(2)同(1)的方法画出即可;(3)将点(-3,-2)的坐标分别代入这两个函数解析式中,看它是否满足这两个函数解析式.www.21-cn-jy.com
解:(1)取自变量的一些值,例如:x=…,-3,-2,-1,0,1,2,3,…,计算出相应的函数值,可列表如下:【来源:21·世纪·教育·网】
x
…
-3
-2
-1
0
1
2
3
…
y
…
4.5
2
0.5
0
0.5
2
4.5
…
由这一系列的对应值,可以得到一系列的有序实数
对:…,(-3,4.5),(-2,2),(-1,0.5),(0,0),(1,0.5),(2,2),(3,4.5),….
在直角坐标系中,描出这些有序实数对的对应点,用平滑的曲线依次把这些点连接起来,便可得到这个函数的图象,如图①.21世纪教育网版权所有
(2)取自变量的一些值,例如:x=…,-2,-1,0,1,2,…,计算出对应的函数值,可列表如下.
x
…
-2
-1
0
1
2
…
y
…
-1
0
1
2
3
…
由这一系列的对应值,可以得到一系列的有序实数
对:…,(-2,-1),(-1,0),(0,1),(1,2),(2,3),….
在直角坐标系中,描出这些有序实数对的对应点,然后用线连接起来,便可得到这个函数的图象,如图②.
(3)将x=-3代入y=x2,得y=×(-3)2=≠-2,
所以点(-3,-2)不在函数y=x2的图象上;
将x=-3代入y=x+1,得y=-3+1=-2,
所以点(-3,-2)在函数y=x+1的图象上.
11.解:(1)③,①
(2)小芳离开家走了一段路程后来到了一个报亭,在报亭读了一段时间报后,按原路返回家(答案不唯一).
12.解:(1)-4≤x≤4.
(2)y的值分别是2,-2,0.
(3)当y=0时,x的值是-3,-1或4;
当y=4时,x的值是1.5.
(4)当x=1.5时,y的值最大;
当x=-2时,y的值最小.
(5)当-2≤x≤1.5时,y随x的增大而增大;当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小.21cnjy.com
13.解:(1)张强返回时的速度是3 000÷(50-30)=150(米/分).
(2)妈妈原来的速度是=50(米/分);
妈妈提前回家的时间是-50=10(分).
(3)分,分,35分.
第3课时 函数的图象
基础训练
知识点1函数的图象
1.下列图象不能表示y是x的函数的是( )
2.下列四个函数图象中,当x>0时,y随x的增大而减小的是( )
3.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )21·cn·jy·com
A.凌晨4时气温最低为-3 ℃
B.14时气温最高为8 ℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
4.甲、乙两人在操场上赛跑,他们赛跑的路程s(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )2·1·c·n·j·y
A.甲、乙两人进行1 000米赛跑
B.甲先慢后快,乙先快后慢
C.比赛到2分钟时,甲、乙两人跑过的路程相等
D.甲先到达终点
5.(2016·安徽)一段笔直的公路AC长20 km,途中有一处休息点B,AB长15 km,甲、乙两名长跑爱好者同时从点A出发,甲以15 km/h的速度匀速跑至点B,原地休息0.5 h后,再以10 km/h的速度匀速跑至终点C;乙以12 km/h的速度匀速跑至终点C,之后休息.下列选项中,能正确反映甲、乙两人出发后2 h内的运动路程y(km)与时间x(h)之间的函数关系的图象是( )21·世纪*教育网
6.(2016·贵阳)星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续匀速走了60 min后回家,图中的折线段OA—AB—BC表示她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线的是( )www-2-1-cnjy-com
知识点2用描点法画函数的图象
7.已知点A(2,3)在函数y=ax2-x+1的图象上,则a=( )
A.1 B.-1 C.2 D.-2
8.画出函数y=2x-1的图象.
(1)列表:
x
…
-1
0
1
…
y
…
-3
-1
1
…
(2)描点并连线;
(3)判断点A(-3,-5),B(2,-3),C(3,5)是否在函数y=2x-1的图象上;
(4)若点P(m,9)在函数y=2x-1的图象上,求出m的值.
易错点 画函数图象时易忽视自变量的取值范围导致出错
9. 某蜡烛原长20 cm,点燃后每小时燃烧5 cm,求剩余的蜡烛长度y(cm)与点燃的时间x(h)之间的函数解析式,并画出函数的图象.
提升训练
考查角度1利用描点法画函数的图象(描点法)
10.(1)画出函数y=x2的图象;
(2)画出函数y=x+1的图象;
(3)试判断点(-3,-2)是否在上述函数图象上.
考查角度2利用图象与情景间的关系互化
11.在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个情境:
情境a:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境b:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境a,b所对应的函数图象分别为________;(填写序号)?
(2)请你为剩下的函数图象写出一个适合的情境.
探究培优
拔尖角度1利用图象反映的信息说明其数学意义
12.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少?
(3)当y=0,4时,x的值分别是多少?
(4)当x取何值时,y的值最大?当x取何值时,y的值最小?
(5)当x的值在什么范围内时,y随x的增大而增大?当x的值在什么范围内时,y随x的增大而减小?
拔尖角度2利用图象反映的信息说明其实际意义
13.某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象.根据图象信息解答下列问题:2-1-c-n-j-y
(1)求张强返回时的速度.
(2)妈妈比按原速返回提前多少分到家?
(3)请直接写出张强与妈妈何时相距1 000米.
参考答案
1.【答案】C
2.【答案】B
3.【答案】C
解:A.∵由图象可知,在凌晨4时函数图象在最低点,∴凌晨4时气温最低为-3 ℃,故本选项正确;B.∵由图象可知,在14时函数图象在最高点,∴14时气温最高为8 ℃,故本选项正确;C.∵由图象可知,从4时至14时,气温随时间增长而上升,不是从0时,故本选项错误;D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.故选C.
4.【答案】C
解:观察函数图象可知:甲、乙两人进行1 000米赛跑;甲在前2.5分钟内,比乙慢,而在后面的时间内比乙快;甲跑完全程用时3.25分钟,乙跑完全程用时4分钟,所以甲先到达终点;比赛到2分钟时,甲跑的路程是500米,乙跑的路程是600米,两人跑过的路程不相等,综上可知选项A,B,D正确,选项C错误.21*cnjy*com
5.【答案】A
6.【答案】B
解:根据给定s关于t的函数图象,分析AB段可得出该段时间蕊蕊妈妈绕以家为圆心的圆弧进行运动,由此即可得出结论.21教育网
7.【答案】A
8.解:(2)如图.
(3)当x=-3时,y=2×(-3)-1=-7≠-5;当x=2时,y=2×2-1=3≠-3;当x=3时,y=2×3-1=5.∴点A,B不在函数y=2x-1的图象上,点C在其图象上.
(4)∵点P(m,9)在函数y=2x-1的图象上,∴2m-1=9,解得m=5.
9.解:根据题意得
y=20-5x(0≤x≤4).
函数图象如图.
10.分析:(1)用描点法(即列表、描点、连线的方法)画出该函数的图象即可.因为自变量x的取值范围为全体实数,所以在列表时可在x=0的两侧对称地取x的值,然后计算出相应的y的值;(2)同(1)的方法画出即可;(3)将点(-3,-2)的坐标分别代入这两个函数解析式中,看它是否满足这两个函数解析式.www.21-cn-jy.com
解:(1)取自变量的一些值,例如:x=…,-3,-2,-1,0,1,2,3,…,计算出相应的函数值,可列表如下:【来源:21·世纪·教育·网】
x
…
-3
-2
-1
0
1
2
3
…
y
…
4.5
2
0.5
0
0.5
2
4.5
…
由这一系列的对应值,可以得到一系列的有序实数
对:…,(-3,4.5),(-2,2),(-1,0.5),(0,0),(1,0.5),(2,2),(3,4.5),….
在直角坐标系中,描出这些有序实数对的对应点,用平滑的曲线依次把这些点连接起来,便可得到这个函数的图象,如图①.21世纪教育网版权所有
(2)取自变量的一些值,例如:x=…,-2,-1,0,1,2,…,计算出对应的函数值,可列表如下.
x
…
-2
-1
0
1
2
…
y
…
-1
0
1
2
3
…
由这一系列的对应值,可以得到一系列的有序实数
对:…,(-2,-1),(-1,0),(0,1),(1,2),(2,3),….
在直角坐标系中,描出这些有序实数对的对应点,然后用线连接起来,便可得到这个函数的图象,如图②.
(3)将x=-3代入y=x2,得y=×(-3)2=≠-2,
所以点(-3,-2)不在函数y=x2的图象上;
将x=-3代入y=x+1,得y=-3+1=-2,
所以点(-3,-2)在函数y=x+1的图象上.
11.解:(1)③,①
(2)小芳离开家走了一段路程后来到了一个报亭,在报亭读了一段时间报后,按原路返回家(答案不唯一).
12.解:(1)-4≤x≤4.
(2)y的值分别是2,-2,0.
(3)当y=0时,x的值是-3,-1或4;
当y=4时,x的值是1.5.
(4)当x=1.5时,y的值最大;
当x=-2时,y的值最小.
(5)当-2≤x≤1.5时,y随x的增大而增大;当-4≤x≤-2或1.5≤x≤4时,y随x的增大而减小.21cnjy.com
13.解:(1)张强返回时的速度是3 000÷(50-30)=150(米/分).
(2)妈妈原来的速度是=50(米/分);
妈妈提前回家的时间是-50=10(分).
(3)分,分,35分.
