3.3中心对称 课时1同步练习

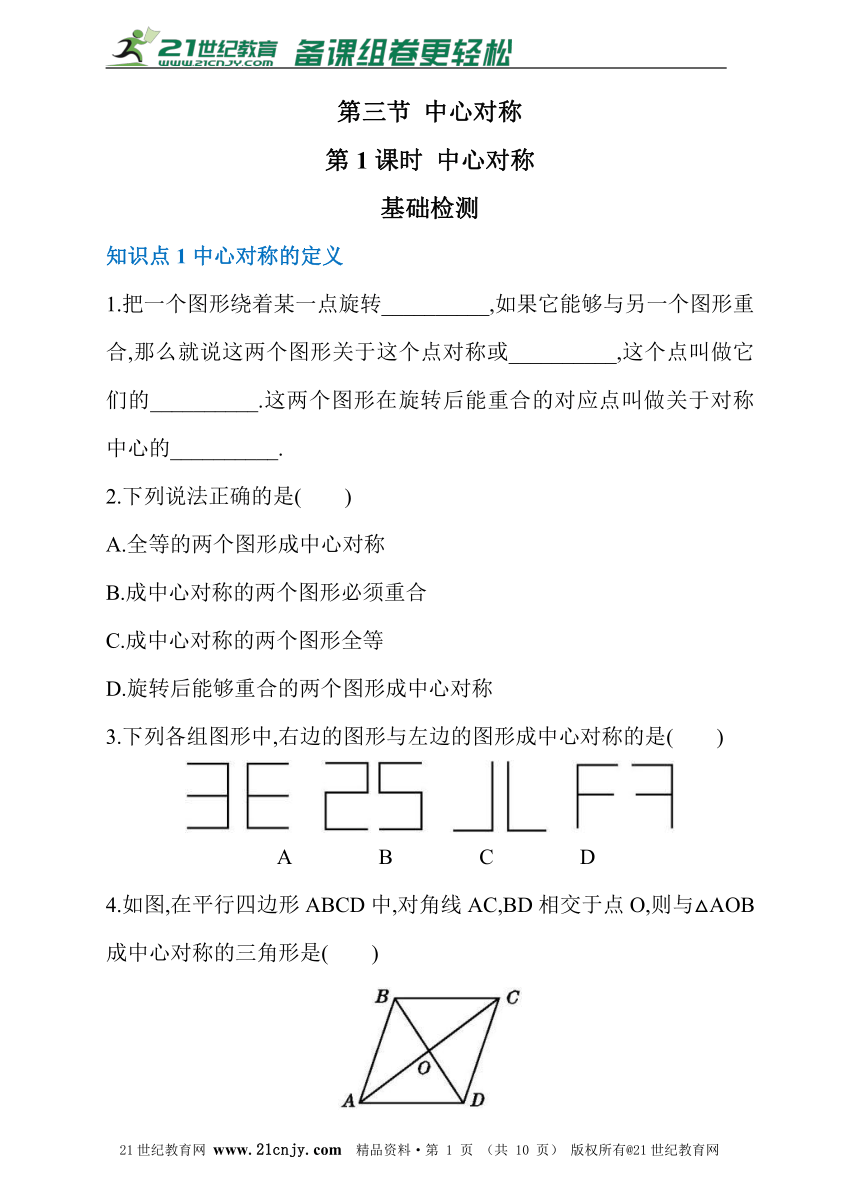
第三节 中心对称
第1课时 中心对称
基础检测
知识点1中心对称的定义
1.把一个图形绕着某一点旋转__________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或__________,这个点叫做它们的__________.这两个图形在旋转后能重合的对应点叫做关于对称中心的__________.?21教育网
2.下列说法正确的是(　　)
A.全等的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等
D.旋转后能够重合的两个图形成中心对称
3.下列各组图形中,右边的图形与左边的图形成中心对称的是(　　)
　　　　 A　　　　B　　　　C　　　　D
4.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,则与△AOB成中心对称的三角形是(　　)21cnjy.com
A.△BOC 　B.△COD
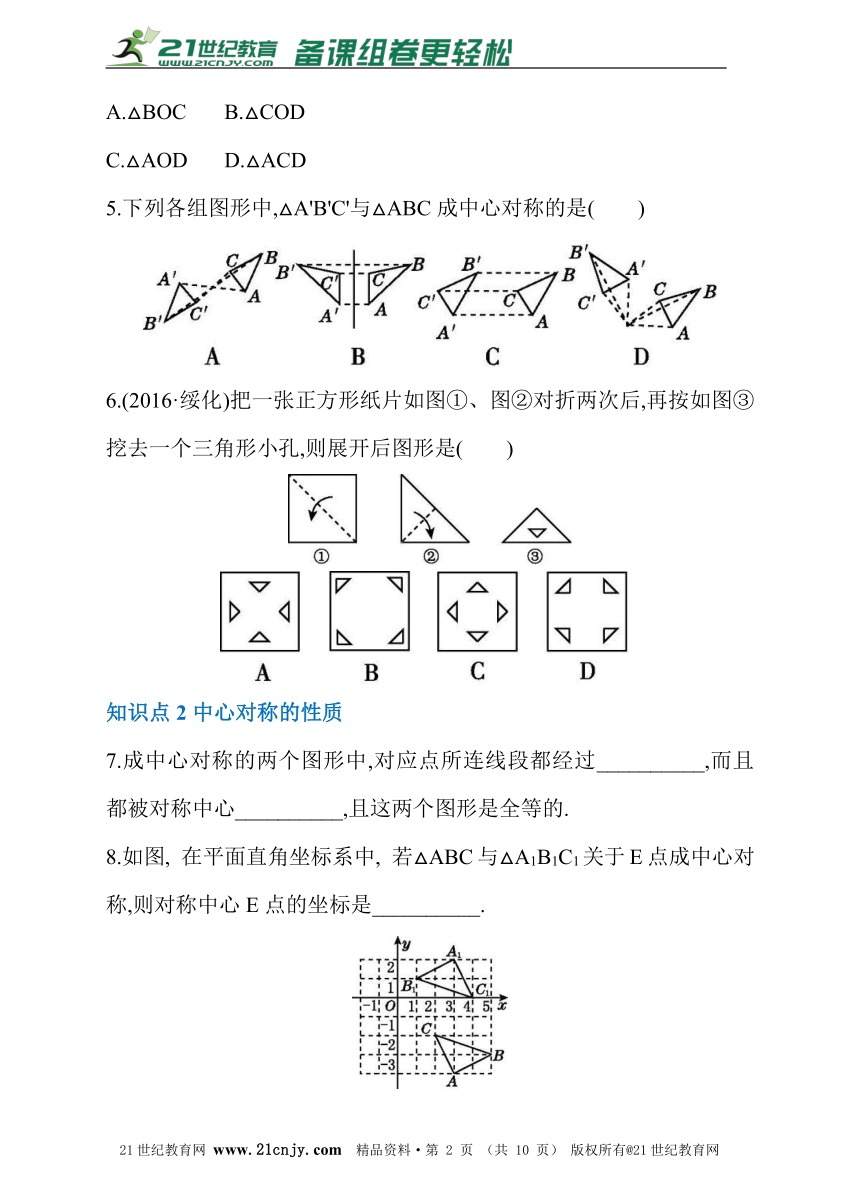
C.△AOD 　D.△ACD
5.下列各组图形中,△A'B'C'与△ABC成中心对称的是(　　)
6.(2016·绥化)把一张正方形纸片如图①、图②对折两次后,再按如图③挖去一个三角形小孔,则展开后图形是(　　)21·cn·jy·com
知识点2中心对称的性质
7.成中心对称的两个图形中,对应点所连线段都经过__________,而且都被对称中心__________,且这两个图形是全等的.?【来源：21·世纪·教育·网】
8.如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是__________.?21·世纪*教育网
9.如图,△ABC与△A1B1C1关于点O成中心对称,下列结论:
①∠BAC=∠B1A1C1;
②AC=A1C1;
③OA=OA1;
④△ABC与△A1B1C1的面积相等,
其中正确的有(　　)
A.1个 B.2个 C.3个 D.4个
知识点3中心对称的作图
10.作点A关于点O的对称点时,连接AO并延长__________,即可得到点A的对称点;作某个图形关于点O的对称图形时,www-2-1-cnjy-com
先作出图形的__________关于点O的对称点,然后顺次连接各对称点即可.?
11.如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.
(1)画△A'B'C',使△A'B'C'与△ABC关于点M成中心对称;
(2)画△A″B″C″,使△A″B″C″与△ABC关于点O成中心对称.
培优提升
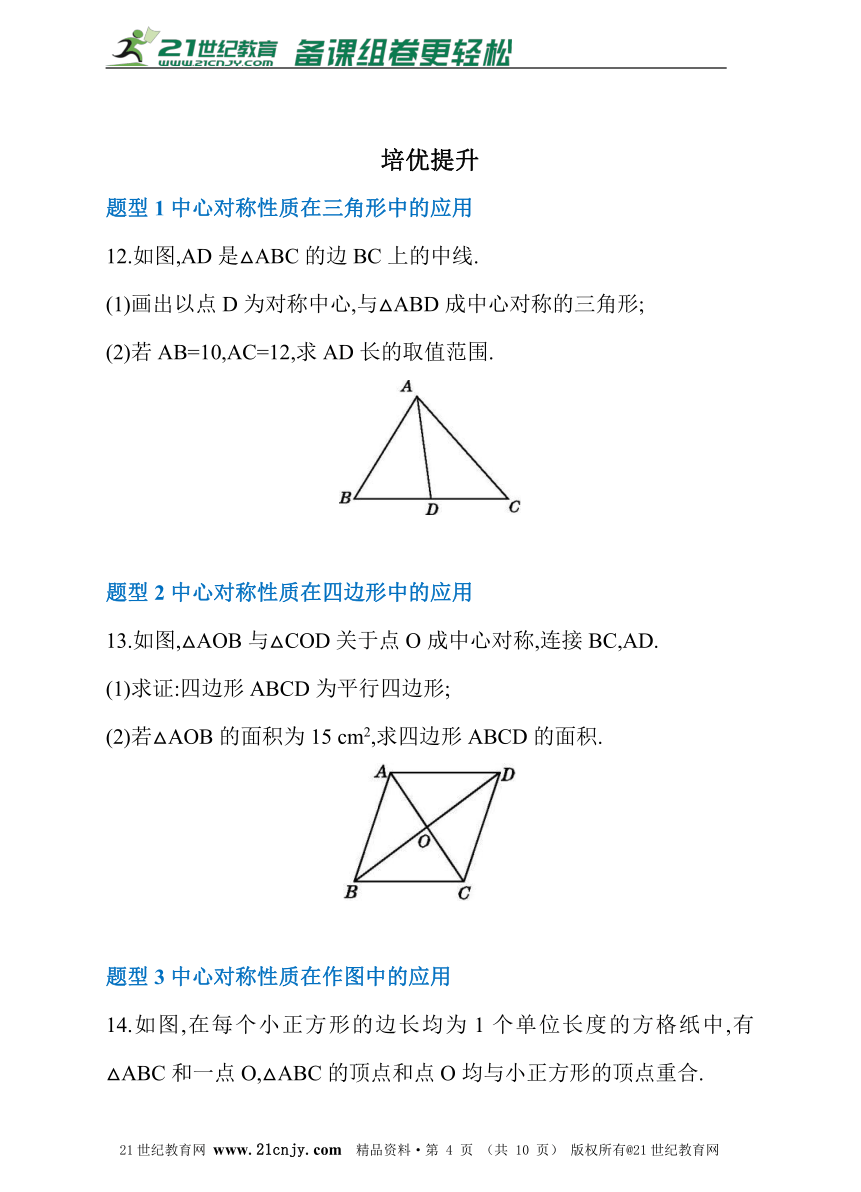
题型1中心对称性质在三角形中的应用
12.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
题型2中心对称性质在四边形中的应用
13.如图,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.
题型3中心对称性质在作图中的应用
14.如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.
(1)在方格纸中,将△ABC向下平移5个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)在方格纸中,将△ABC绕点O旋转180°得到△A2B2C2,请画出△A2B2C2.
题型4中心对称性质在坐标系中的应用
15.(2016·聊城)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).www.21-cn-jy.com
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;2·1·c·n·j·y
(2)若△ABC和△A2B2C2关于原点O成中心对称,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.2-1-c-n-j-y
16.如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由. 21*cnjy*com
参考答案
1.【答案】180°;中心对称;对称中心;对称点
2.【答案】C
3.【答案】A
解：根据中心对称的概念，A图都是中心对称；故选A．
4.【答案】B 5.【答案】A
6.【答案】C
解：当正方形纸片两次沿对角线对折成为一直角三角形时，在直角三角形中间的位置上剪三角形，则直角顶点处完好，即原正方形中间无损，且三角形关于对角线对称，三角形的一个顶点对着正方形的边。
故选C。
7.【答案】对称中心;平分　
8.【答案】(3,-1) 9.【答案】D
10.【答案】一倍;每个关键点
11.解:如图.(1)①连接AM并延长至A',使MA'=AM;　
②点B关于点M的对称点B'即为点C,点C关于点M的对称点C'即为点B;
③连接A'B',A'C',则△A'B'C'即为所求.
(2)①连接AO,BO,CO,并分别延长至A″,B″,C″,
使OA″=AO,OB″=BO,OC″=CO;
②连接A″B″,A″C″,B″C″,则△A″B″C″即为所求.
12.解:(1)如图,△ECD为所求.
(2)由(1)可知AD=DE,EC=AB=10.
在△ACE中,由AC-EC12-10又∵AE=2AD,
∴2<2AD<22,∴113.(1)证明:∵△AOB与△COD关于点O成中心对称,
∴△AOB≌△COD.
∴OA=OC,OB=OD,∠OAB=∠OCD.
又∵∠AOD=∠COB,∴△AOD≌△COB(SAS).
∴∠OAD=∠OCB.∴AB∥CD,AD∥BC.
∴四边形ABCD为平行四边形.
(2)解:由(1)知△AOB,△BOC,△COD,△AOD的面积相等.∴S四边形ABCD=4S△AOB=4×15=60(cm2).　21世纪教育网版权所有
14.解:(1)△A1B1C1如图所示.(2)△A2B2C2如图所示.
15.解:(1)如图,∵点C(-1,3)平移后的对应点C1的坐标为(4,0),∴△ABC先向右平移5个单位长度,再向下平移3个单位长度得到△A1B1C1.
∴顶点A1的坐标为(2,2).顶点B1的坐标为(3,-2).
(2)∵△ABC和△A2B2C2关于原点O成中心对称,
∴A2(3,-5),B2(2,-1),C2(1,-3).
(3)如图,A3(5,3),B3(1,2),C3(3,1).
16.解:FC2+BE2=EF2.理由如下:
∵点D为BC的中点,∴BD=CD.作△BDE关于点D成中心对称的
△CDM,如图.
由中心对称的性质可得CM=BE,MD=ED,∠DCM=∠B.
又∵∠B+∠ACB=90°,
∴∠DCM+∠ACB=90°,即∠FCM=90°.
连接FM.在△FME中,MD=ED,FD⊥ME,FD=FD,
∴△FDM≌△FDE.∴FM=EF.
又∵在Rt△FCM中,FC2+CM2=FM2,　
∴FC2+BE2=EF2.