第3章图形与坐标 单元测试

湘教版八年级下第3章图形与坐标测试
姓名：__________班级：__________考号：__________
一．选择题（共12小题）
1．根据下列表述，能确定位置的是（　　）
A．红星电影院2排 B．北京市四环路 C．北偏东30° D．东经118°，北纬40°
2．如图，下列各点在阴影区域内的是（　　）
A．（3，2） B．（﹣3，2） C．（3，﹣2） D．（﹣3，﹣2）
3．点A（﹣2，﹣3）和点B（2，﹣3）在平面直角坐标系中（　　）
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．不关于坐标轴和原点对称
4．点P在第三象限内，P到X轴的距离与到y轴的距离之比为2：1，到原点的距离为，则点P的坐标
（　　）
A．（﹣1，2） B．（﹣2，﹣1） C．（﹣1，﹣2） D．（1，﹣2）
5．一个长方形在平面直角坐标系中三个顶点的坐标为（﹣1，﹣1），（﹣1，2），（3，﹣1），则第四个顶点的坐标为（　　）21·世纪*教育网
A．（2，2） B．（3，2） C．（3，3） D．（2，3）
6．如图，在平面直角坐标系中，点P（﹣1，2）关于直线x=1的对称点的坐标为（　　）
A．（1，2） B．（2，2） C．（3，2） D．（4，2）
7．若点P（a，2）与Q（﹣1，b）关于坐标原点对称，则a，b分别为（　　）
A．﹣1，2 B．1，﹣2 C．1，2 D．﹣1，﹣2
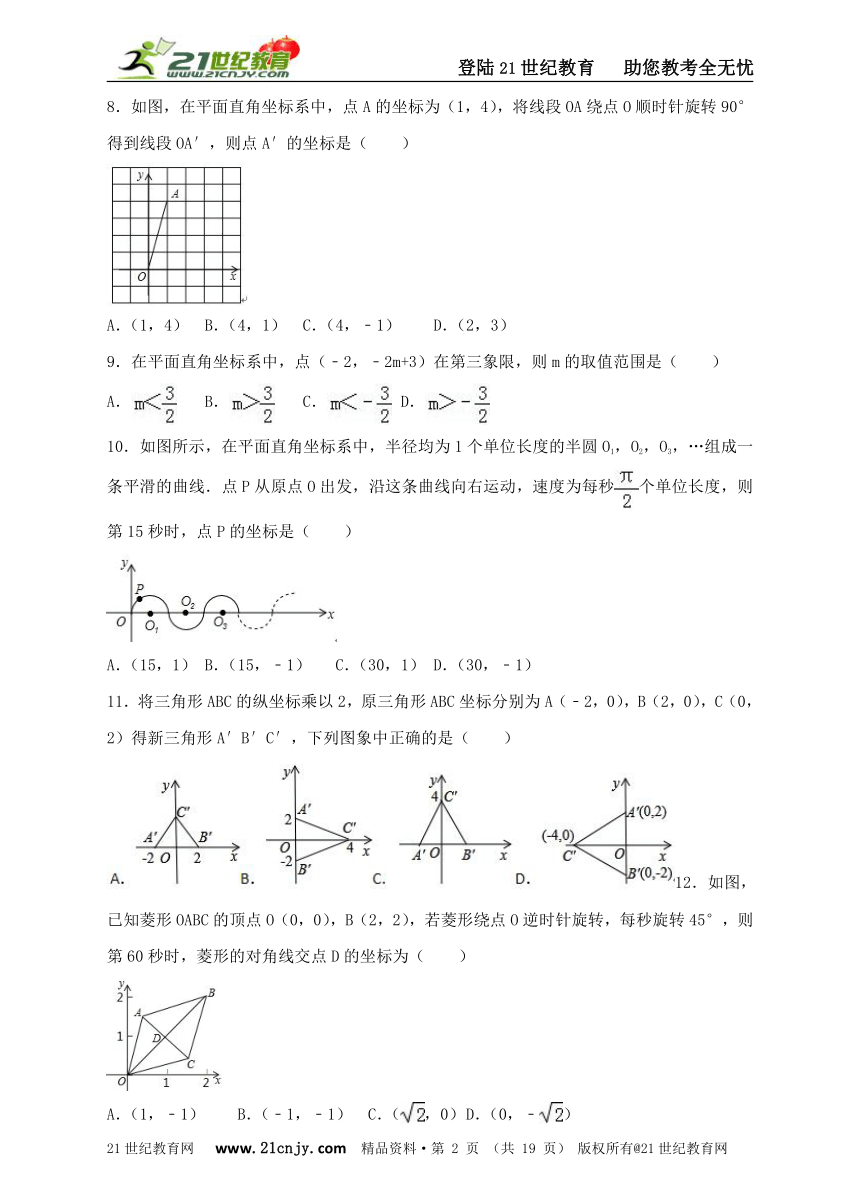
8．如图，在平面直角坐标系中，点A的坐标为（1，4），将线段OA绕点O顺时针旋转90°得到线段OA′，则点A′的坐标是（　　）21*cnjy*com
A．（1，4） B．（4，1） C．（4，﹣1） D．（2，3）
9．在平面直角坐标系中，点（﹣2，﹣2m+3）在第三象限，则m的取值范围是（　　）
A． B． C． D．
10．如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线．点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第15秒时，点P的坐标是（　　）
A．（15，1） B．（15，﹣1） C．（30，1） D．（30，﹣1）
11．将三角形ABC的纵坐标乘以2，原三角形ABC坐标分别为A（﹣2，0），B（2，0），C（0，2）得新三角形A′B′C′，下列图象中正确的是（　　）2·1·c·n·j·y
12．如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（　　）
A．（1，﹣1） B．（﹣1，﹣1） C．（，0） D．（0，﹣）
二．填空题（共6小题）
13．点E（a，﹣5）与点F（﹣2，b）关于y轴对称，则a=　　，b=　　．
14．点P到x轴的距离是2，到y轴的距离是3，且在y轴的左侧，则P点的坐标是　　．
15．在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：
①△（a，b）=（﹣a，b）；
②○（a，b）=（﹣a，﹣b）；
③Ω（a，b）=（a，﹣b），
按照以上变换例如：△（○（1，2））=（1，﹣2），则○（Ω（3，4））等于　　．
16．在平面直角坐标系中，已知点A（﹣，0），B（，0），点C在x轴上，且AC+BC=6，写出满足条件的所有点C的坐标　　．
17．如图，在平面直角坐标系中，线段OA与线段OA′关于直线l：y=x对称．已知点A的坐标为（2，1），则点A′的坐标为　　．
18．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你观察图中正方形A1B1C1D1，A2B2C2D2，A3B3C3D3…每个正方形四条边上的整点的个数．按此规律推算出正方形A10B10C10D10四条边上的整点共有　　个．
三．解答题（共8小题）
19．如图中，A、B两点的坐标分别为（2，3）、（4，1），
（1）求△ABO的面积．
（2）把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
20．如图，一个小正方形网格的边长表示50米．A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校．
（1）以学校为坐标原点，向东为x轴正方向，向北为y轴正方向，在图中建立直角坐标系：
（2）B同学家的坐标是　　；
（3）在你所建的直角坐标系中，如果C同学家的坐标为（﹣150，100），请你在图中描出表示C同学家的点．
21．在平面直角坐标系中，分别描出点A（﹣1，0），B（0，2），C（1，0），D（0，﹣2）．
（1）试判断四边形ABCD的形状；
（2）若B、D两点不动，你能通过变动点A、C的位置使四边形ABCD成为正方形吗？若能，请写出变动后的点A、C的坐标．
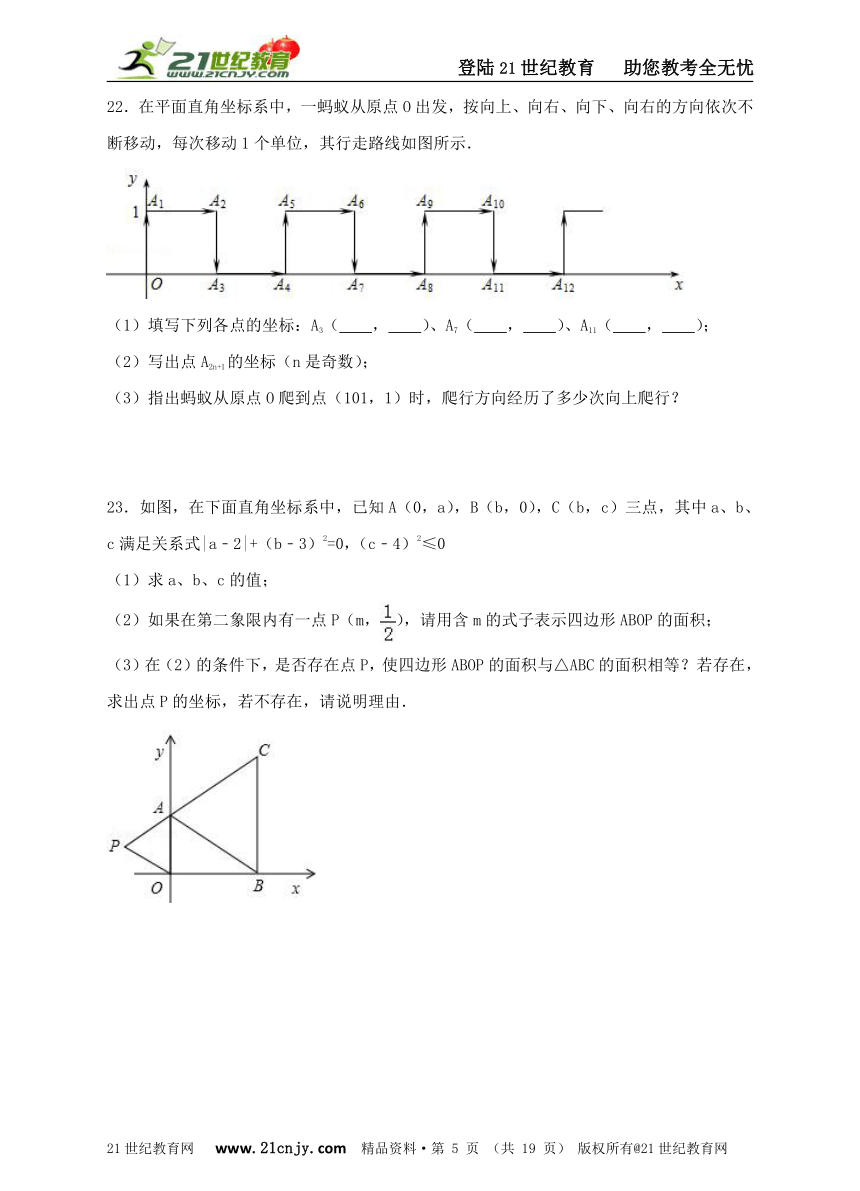
22．在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如图所示．
（1）填写下列各点的坐标：A3（　　，　　）、A7（　　，　　）、A11（　　，　　）；
（2）写出点A2n+1的坐标（n是奇数）；
（3）指出蚂蚁从原点O爬到点（101，1）时，爬行方向经历了多少次向上爬行？
23．如图，在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式|a﹣2|+（b﹣3）2=0，（c﹣4）2≤0【来源：21·世纪·教育·网】
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．
24．已知点P（2a﹣12，1﹣a）位于第三象限，点Q（x，y）位于第二象限且是由点P向上平移一定单位长度得到的．
（1）若点P的纵坐标为﹣3，试求出a的值；
（2）在（1）题的条件下，试求出符合条件的一个点Q的坐标；
（3）若点P的横、纵坐标都是整数，试求出a的值以及线段PQ长度的取值范围．
25．如图，在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式|a﹣2|+（b﹣3）2=0和（c﹣4）2≤0；
（1）求a、b、c的值；
（2）如果在第二象限内有一点p（m，），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使得四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．
26．如图所示，△ABC在平面直角坐标系中，△A1B1C1与△ABC关于y轴对称，将△ABC向右平移m个单位得到△A2B2C2，已知A（﹣3，4），B（﹣6，0），C（﹣2，0）．
（1）在备用图1中画出△A1B1C1；
（2）m为何值时，点A1与A2重合？并说明B2C1=B1C2；
（3）m为何值时，△A1B1C1与△A2B2C2一边重合？若A1B1与A2B2并交于P点，请证明PA1=PA2；
（4）m为何值时，B2、C2的横坐标是某正数的两个不同的平方根？
　
参考答案与试题解析
　
一．选择题（共12小题）
1．分析: 根据在平面内，要有两个有序数据才能清楚地表示出一个点的位置，即可得答案．
解：在平面内，点的位置是由一对有序实数确定的，只有D能确定一个位置，
故选：D．
　
2．分析: 应先判断出阴影区域在第一象限，进而判断在阴影区域内的点．
解：观察图形可知：阴影区域在第一象限，
A、（3，2）在第一象限，故正确；
B、（﹣3，2）在第二象限，故错误；
C、（3，﹣2）在第四象限，故错误；
D、（﹣3，﹣2）在第三象限，故错误．
故选A．
　
3．分析: 根据关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得答案．
解：∵点A（﹣2，﹣3）和点B（2，﹣3），纵坐标不变，横坐标互为相反数，
∴关于y轴对称，
故选：B．
　
4．分析: 应先判断出点P的横纵坐标的符号，进而根据点P到坐标轴的距离，到原点的距离判断具体坐标．
解：∵点P在第三象限内，
∴点P的横纵坐标均为负，
∵P到X轴的距离与到y轴的距离之比为2：1，
∴可设P的横坐标为x，纵坐标为2x，
∵点P到原点的距离为，
∴x2+（2x）2=5，
∴x=±1，
∴x=﹣1，
∴点P的坐标为（﹣1，﹣2）．
故选C．
　
5．分析: 本题可在画出图后，根据矩形的性质，得知第四个顶点的横坐标应为3，纵坐标应为2．
解：如图可知第四个顶点为：

即：（3，2）．
故选：B．
　
6．分析: 先求出点P到直线x=1的距离，再根据对称性求出对称点P′到直线x=1的距离，从而得到点P′的横坐标，即可得解．21cnjy.com
解：∵点P（﹣1，2），
∴点P到直线x=1的距离为1﹣（﹣1）=2，
∴点P关于直线x=1的对称点P′到直线x=1的距离为2，
∴点P′的横坐标为2+1=3，
∴对称点P′的坐标为（3，2）．
故选C．
　
7．分析: 平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），那么，即可求得a与b的值．www.21-cn-jy.com
解：∵点P（a，2）与Q（﹣1，b）关于坐标原点对称，
∴a，b分别为1，﹣2；
故本题选B．
　
8．分析: 线段旋转后长度不会变化，然后根据三角形的全等算出A'的坐标．
解：如图：∵∠AOB+∠AOC=∠AOC+∠A′OC=90°，
∴∠AOB=∠A′OC，
∵OA=OA′，∠A′CO=∠ABO=90°，
∴△ABO≌△A′BO，
∴A′C=AB OC=OB．
因为A′位于第四象限，则A′坐标为（4，﹣1）．
故选C．
　
9．分析: 点在第三象限的条件是：横坐标是负数，纵坐标是负数，可得﹣2m+3＜0，求不等式的解即可．2-1-c-n-j-y
解：∵点在第三象限，
∴点的横坐标是负数，纵坐标也是负数，
即﹣2m+3＜0，
解得m＞．
故选B．
　
10．分析: 以时间为点P的下标，根据半圆的半径以及部分P点的坐标找出规律“P4n（n，0），P4n+1（4n+1，1），P4n+2（0，4n+2），P4n+3（4n+3，﹣1）”，根据此规律即可找出第15秒时，点P的坐标．21*cnjy*com
解：观察，发现规律：P0（0，0），P1（1，1），P2（0，2），P3（3，﹣1），P4（4，0），P5（5，1），P6（0，6），…，【出处：21教育名师】
∴P4n（n，0），P4n+1（4n+1，1），P4n+2（0，4n+2），P4n+3（4n+3，﹣1）．
∵15=3×4+3，
∴第15秒时，点P的坐标为（15，﹣1）．
故选B．
　
11．分析: 将三角形ABC的纵坐标乘以2后，坐标分别为A′（﹣2，0），B′（2，0），C′（0，4）即可选出答案．【来源：21cnj*y.co*m】
解：将A（﹣2，0），B（2，0），C（0，2）三点的纵坐标乘以2后得：A′（﹣2，0），B′（2，0），C′（0，4），对照四选项可知C正确．故选C．21教育名师原创作品
　
12．分析: 根据菱形的性质，可得D点坐标，根据旋转的性质，可得D点的坐标．
解：菱形OABC的顶点O（0，0），B（2，2），得
D点坐标为（1，1）．
每秒旋转45°，则第60秒时，得
45°×60=2700°，
2700°÷360=7.5周，
OD旋转了7周半，菱形的对角线交点D的坐标为（﹣1，﹣1），
故选：B．
　
二．填空题（共6小题）
13．分析: 关于y轴对称的点，纵坐标相同，横坐标互为相反数．
解：根据平面直角坐标系中对称点的规律可知，点E（a，﹣5）与点F（﹣2，b）关于y轴对称，
则a=2，b=﹣5．
故答案为：2；﹣5．
　
14．分析: 根据直角坐标系中，某点到x轴的距离是它的纵坐标的绝对值，到y轴的确距离是它的横坐标的绝对值解答．
解：∵P（x，y）到x轴的距离是2，到y轴的距离是3，
∴x=±3，y=±2；
又∵点P在y轴的左侧，
∴点P的横坐标x=﹣3，
∴点P的坐标为（﹣3，2）或（﹣3，﹣2）．故填（﹣3，2）或（﹣3，﹣2）．
　
15．分析: 根据三种变换规律的特点解答即可．
解：○（Ω（3，4））=○（3，﹣4）=（﹣3，4）．
故答案为：（﹣3，4）．
　
16．分析: 设点C到原点O的距离为a，然后根据AC+BC=6列出方程求出a的值，再分点C在x轴的左边与右边两种情况讨论求解．
解：设点C到原点O的距离为a，
∵AC+BC=6，
∴a﹣+a+=6，
解得a=3，
∴点C的坐标为（3，0）或（﹣3，0）．
故答案为：（3，0）或（﹣3，0）．
　
17．分析: 根据线段OA与线段OA′关于直线l：y=x对称得出∠A′OD=∠AOD，OA′=OA，进而求出△A′C′O≌△ACO，即可得出点A′的坐标．
解：过点A作AC⊥x轴于点C，过点A′作A′C′⊥y轴于点C′，连接AA′，
∵线段OA与线段OA′关于直线l：y=x对称，
∴△ODA′≌△ODA，∠C′OD=∠DOC，
∴∠A′OD=∠AOD，OA′=OA，
∴在△A′C′O和△ACO中，
，
∴△A′C′O≌△ACO，
∴AC=A′C′，CO=OC′，
∵点A的坐标为（2，1），
∴点A′的坐标为（1，2），
故答案为：（1，2）．
　
18．分析: 根据题意可知：A1B1C1D1四条边上的整点共有4+4×1=8，A2B2C2D2四条边上的整点共有4+4×3=16，正方形A3B3C3D3四条边上的整点的个数有4+4×5=24，依此类推得到算式是4+4×19，即可求出答案．www-2-1-cnjy-com
解：A1B1C1D1四条边上的整点共有8个，即4+4×1=8，
A2B2C2D2四条边上的整点共有16个，即4+4×3=16，
正方形A3B3C3D3四条边上的整点的个数有4+4×5=24，
…正方形A10B10C10D10四条边上的整点的个数有：4+4×19=80，
故答案为：80．
　
三．解答题（共8小题）
19．分析: （1）把△ABO放在一个矩形里面，用矩形COED的面积﹣△ACO的面积﹣△ABD的面积﹣△BEO的面积即可算出△ABO的面积；
（2）根据点的坐标平移的规律，用A、B、O的坐标的纵坐标分别减去3即可．
解：（1）如图所示：
S△ABO=3×4﹣×3×2﹣×4×1﹣×2×2=5；
（2）A′（2，0），B′（4，﹣2），O′（0，﹣3）．
　
20．分析: （1）由于A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校，则可确定A点位置，然后画出直角坐标系；
（2）利用第一象限点的坐标特征写出B点坐标；
（3）根据坐标的意义描出点C．
解：（1）如图，
（2）B同学家的坐标是（200，150）；
（3）如图．
故答案为（200，150）．
　
21．分析: （1）在坐标轴上找出横坐标和纵坐标，即可找到相应的点，根据图形及坐标即可判断其形状；
（2）由正方形也属于菱形，只要对角线互相垂直平分即可据此求出A、C点的坐标．

解：（1）作出四个点的坐标：
四边形ABCD是菱形．
因为：对角线互相垂直且互相平分．
（2）能（10分）
变动后的A点坐标为（2，0），
C点坐标为（﹣2，0）．
　
22．分析: （1）观察图形可知，A3，A7，A11在x轴上，求出OA3、OA7，OA11长度，然后写出坐标即可；21教育网
（2）根据（1）中规律写出点A2n+1的坐标即可；
（3）根据每4个点为一个循环组依次循环，可知点A202（101，1），每4个点里面有一次向上爬行，202÷4=50…2，即可解答．
解：（1）由图可知，A3，A7，A11都在x轴上，
∵小蚂蚁每次移动1个单位，
∴OA3=1，OA7=3，OA11=5，
∴A3（1，0），A7（3，0），A11（5，0）；
故答案为：2，0；3，0；5，0；
（2）根据（1）的规律可得：A2n+1（n，0）；
（3）∵每4个点为一个循环组依次循环，
∴点A202（101，1），
∵每4个点里面有一次向上爬行，且第一次爬行向上，202÷4=50…2，
∴蚂蚁从原点O爬到点（101，1）时，爬行方向经历了50+1=51次向上爬行．
　
23．分析: （1）用非负数的性质求解；
（2）把四边形ABOP的面积看成两个三角形面积和，用m来表示；
（3）△ABC可求，是已知量，根据题意，方程即可．
解：（1）由已知|a﹣2|+（b﹣3）2=0，（c﹣4）2≤0及（c﹣4）2≥0
可得：a=2，b=3，c=4；
（2）∵×2×3=3，×2×（﹣m）=﹣m，
∴S四边形ABOP=S△ABO+S△APO=3+（﹣m）=3﹣m
（3）因为×4×3=6，
∵S四边形ABOP=S△ABC
∴3﹣m=6，
则 m=﹣3，
所以存在点P（﹣3，）使S四边形ABOP=S△ABC．
　
24．分析: （1）点P的纵坐标为﹣3，即1﹣a=﹣3；解可得a的值；
（2）根据题意：由a=4得：2a﹣12=﹣4；进而根据又点Q（x，y）位于第二象限，所以y＞0；取符合条件的值，可得Q的坐标；【版权所有：21教育】
（3）根据点P（2a﹣12，1﹣a）位于第三象限，且横、纵坐标都是整数，可得；
解而求其整数解可得a的值以及线段PQ长度的取值范围．
解：
（1）1﹣a=﹣3，a=4．
（2）由a=4得：2a﹣12=2×4﹣12=﹣4，又点Q（x，y）位于第二象限，所以y＞0；
取y=1，得点Q的坐标为（﹣4，1）．
（3）因为点P（2a﹣12，1﹣a）位于第三象限，
所以，
解得：1＜a＜6．
因为点P的横、纵坐标都是整数，所以a=2或3或4或5；
当a=2时，1﹣a=﹣1，所以PQ＞1；
当a=3时，1﹣a=﹣2，所以PQ＞2；
当a=4时，1﹣a=﹣3，所以PQ＞3；
当a=5时，1﹣a=﹣4，所以PQ＞4．
　
25．分析: （1）根据非负数的性质，即可解答；
（2）四边形ABOP的面积=△APO的面积+△AOB的面积，即可解答；
（3）存在，根据面积相等求出m的值，即可解答．
解：（1）由已知|a﹣2|+（b﹣3）2=0，（c﹣4）2≤0可得：
a﹣2=0，b﹣3=0，c﹣4=0，
解得：a=2，b=3，c=4；
（2）∵a=2，b=3，c=4，
∴A（0，2），B（3，0），C（3，4），
∴OA=2，OB=3，
∵S△ABO=×2×3=3，
S△APO=×2×（﹣m）=﹣m，
∴S四边形ABOP=S△ABO+S△APO=3+（﹣m）=3﹣m
（3）存在，
∵S△ABC=×4×3=6，
若S四边形ABOP=S△ABC=3﹣m=6，则m=﹣3，
∴存在点P（﹣3，）使S四边形ABOP=S△ABC．
　
26．分析: （1）让各点的横坐标不变，纵坐标互为相反数即可得到A1，B1，C1的坐标，顺从连接即可；21世纪教育网版权所有
（2）让点A1的横坐标减去点A的横坐标即可求得m的值；
（3）让点B1的横坐标减去点B的横坐标即可求得m的值；可证得PA1和PA2所在的三角形全等，那么可求得两边相等；21·cn·jy·com
（4）B2C2之间相隔4，要想为一个正数的两个平方根，那么B2的横坐标应为﹣2，减去B的横坐标即为m的值．
解：（1）画图如下图：
（2）当点A1与点A2重合时，A2（3，4）
∵A2（﹣3+m，4）
∴m=6（4分）
由B2C2=B1C1
∴B2C1=B1C2
（3）如右图，当m=8时，△A1B1C1与△A2B2C2一边重合，则B2C2与B1C1重合；
∵△A1B1C1≌△A2B2C2
在△A1C1P和△A2C2P中
∴△A1C1P≌△A2C2P
∴PA1=PA2；
（4）当m=4时，B2、C2的横坐标是正数4的两个不同的平方根．（10分）
∵B2（﹣6+m），C2（﹣2+m）
∴（﹣6+m）+（﹣2+m）=0
∴m=4（12分）．