第4章一次函数单元测试 B卷

湘教版八年级下第4章一次函数测试 B卷
　姓名：__________班级：__________考号：__________
一．选择题（共12小题）
1．设半径为r的圆的面积为S，则S=πr2，下列说法错误的是（　　）
A．变量是S和r， B．常量是π和2
C．用S表示r为r= D．常量是π
2．下列各曲线中不能表示y是x的函数的是（　　）
3．下列函数中，与y=x表示同一个函数的是（　　）
A．y= B．y= C．y= D．y=
4．函数y=中自变量x的取值范围是（　　）
A．x≥﹣3 B．x≠5 C．x≥﹣3或x≠5 D．x≥﹣3且x≠5
5．已知函数y=，当x=﹣2时，函数值为（　　）
A． B．± C．3 D．±3
6．如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止．设小三角形移动的距离为x，两个三角形重叠面积为y，则y关于x的函数图象是（　　）21cnjy.com
7．已知y=（m2+2m），如果y是x的正比例函数，则m的值为（　　）
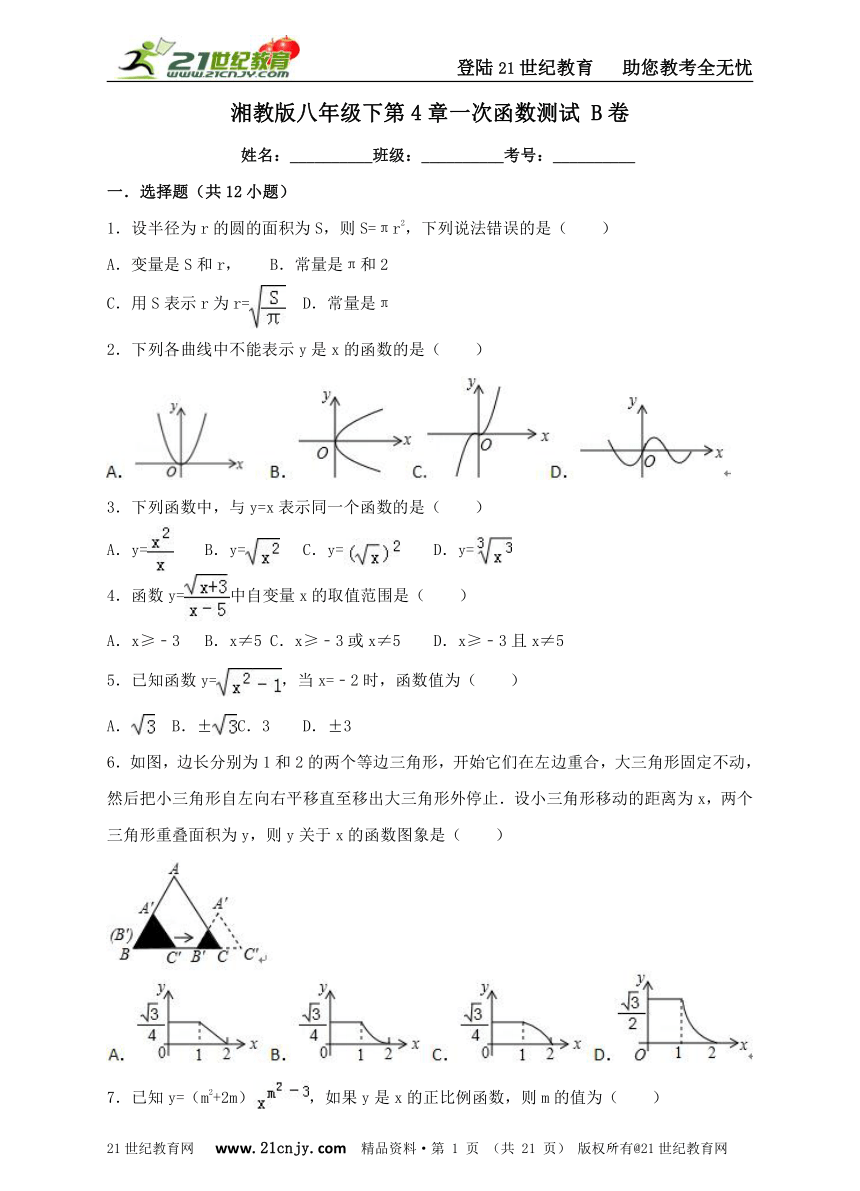
A．2 B．﹣2 C．2，﹣2 D．0
8．下列函数关系中表示一次函数的有（　　）
①y=2x+1 ②③④s=60t ⑤y=100﹣25x．
A．1个 B．2个 C．3个 D．4个
9．已知两个一次函数y1=mx+n，y2=nx+m，它们在同一坐标系中的图象可能是（　　）

10．点A（3，y1）和点B（﹣2，y2）都在直线y=﹣2x+3上，则y1和y2的大小关系是（　　）
A．y1＞y2 B．y1＜y2 C．y1=y2 D．不能确定
11．直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是（　　）
A．（﹣4，0） B．（﹣1，0） C．（0，2） D．（2，0）
12．已知一次函数y=kx+b（k≠0）图象过点（0，2），且与两坐标轴围成的三角形面积为2，则一次函数的解析式为（　　）www-2-1-cnjy-com
A．y=x+2 B．y=﹣x+2
C．y=x+2或y=﹣x+2 D．y=﹣x+2或y=x﹣2
　
二．填空题（共8小题）
13．一次函数y=（m+1）x﹣（4m﹣3）的图象不经过第三象限，那么m的取值范围是　　．
14．某地市话的收费标准为：
（1）通话时间在3分钟以内（包括3分钟）话费0.3元；
（2）通话时间超过3分钟时，超过部分的话费按每分钟0.11元计算．
在一次通话中，如果通话时间超过3分钟，那么话费y（元）与通话时间x（分）之间的关系式为　　．
15．函数y=|x﹣1|+2|x﹣2|+3|x﹣3|+4|x﹣4|的最小值是　　．
16．新定义：[a，b，c]为函数y=ax2+bx+c （a，b，c为实数）的“关联数”．若“关联数”为[m﹣2，m，1]的函数为一次函数，则m的值为　　．21教育名师原创作品
17．若一次函数y=kx+b，当﹣3≤x≤1时，对应的y值为1≤y≤9，则一次函数的解析式为　　．
18．甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中：
①甲队每天挖100米；
②乙队开挖两天后，每天挖50米；
③甲队比乙队提前3天完成任务；
④当x=2或6时，甲乙两队所挖管道长度都相差100米．
正确的有　　．（在横线上填写正确的序号）
19．已知：直线y=﹣x+（n为整数）与两坐标轴围成的三角形面积为sn，则s1+s2+s3+…+sn=　　．21世纪教育网版权所有
20．如图1，E为矩形ABCD边AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．若点P，Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2）．已知y与t的函数关系图象如图2，有下列四个结论：①AE=6cm；②sin∠EBC=；③当0＜t≤10时，y=t2； ④当t=12s时，△PBQ是等腰三角形．其中正确结论的序号是　　．21·世纪*教育网
　
三．解答题（共8小题）
21．画出函数y=2x+6的图象，利用图象：
①求方程2x+6=0的解；
②求不等式2x+6＞0的解；
③若﹣1≤y≤3，求x的取值范围．
22．已知y﹣2与x+1成正比例函数关系，且x=﹣2时，y=6．
（1）写出y与x之间的函数关系式；
（2）求当x=﹣3时，y的值；
（3）求当y=4时，x的值．
23．已知y=（m+1）x2﹣|m|+n+4
（1）当m、n取何值时，y是x的一次函数？
（2）当m、n取何值时，y是x的正比例函数？
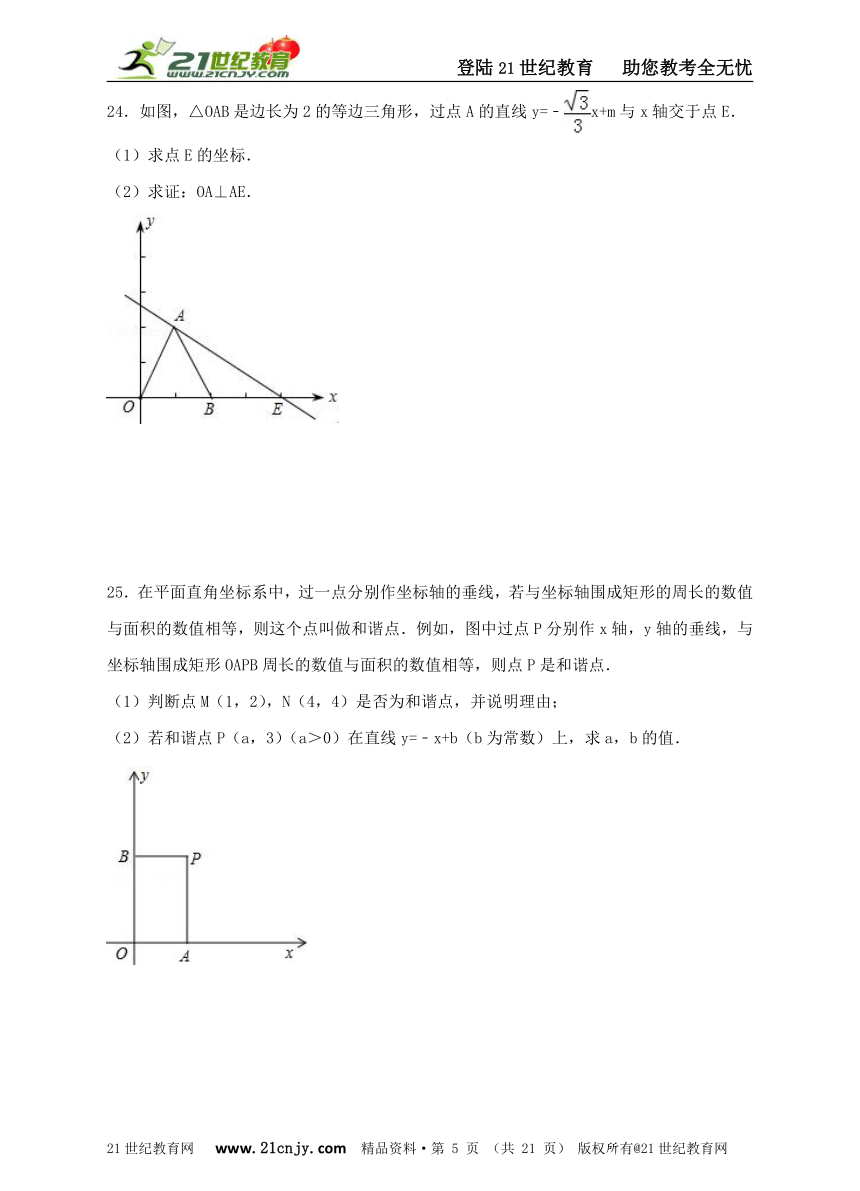
24．如图，△OAB是边长为2的等边三角形，过点A的直线y=﹣x+m与x轴交于点E．
（1）求点E的坐标．
（2）求证：OA⊥AE．
25．在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成矩形的周长的数值与面积的数值相等，则这个点叫做和谐点．例如，图中过点P分别作x轴，y轴的垂线，与坐标轴围成矩形OAPB周长的数值与面积的数值相等，则点P是和谐点．
（1）判断点M（1，2），N（4，4）是否为和谐点，并说明理由；
（2）若和谐点P（a，3）（a＞0）在直线y=﹣x+b（b为常数）上，求a，b的值．
26．（1）点（0，1）向下平移2个单位后的坐标是　　，直线y=2x+1向下平移2个单位后的解析式是　　；21·cn·jy·com
（2）直线y=2x+1向右平移2个单位后的解析式是　　；
（3）如图，已知点C为直线y=x上在第一象限内一点，直线y=2x+1交y轴于点A，交x轴于B，将直线AB沿射线OC方向平移个单位，求平移后的直线的解析式．
27．某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．www.21-cn-jy.com
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
28．阅读下列解题过程，并解答后面的问题：
如图1，在平面直角坐标系xOy中，A（x1，y1），B（x2，y2），C为线段AB的中点，求C点的坐标．2-1-c-n-j-y
解：分布过A、C做x轴的平行线，过B、C做y轴的平行线，两组平行线的交点如图1所示．
设C（x0，y0），则D（x0，y1），E（x2，y1），F（x2，y0）
由图1可知：x0==
y0==
∴（，）
问题：（1）已知A（﹣1，4），B（3，﹣2），则线段AB的中点坐标为　　．
（2）平行四边形ABCD中，点A、B、C的坐标分别为（1，﹣4），（0，2），（5，6），求点D的坐标．21*cnjy*com
（3）如图2，B（6，4）在函数y=x+1的图象上，A（5，2），C在x轴上，D在函数y=x+1的图象上，以A、B、C、D四个点为顶点构成平行四边形，直接写出所有满足条件的D点的坐标．
　

参考答案与试题解析
　
一．选择题（共12小题）
1．分析: 根据函数的定义：对于函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应；来解答即可．
解：∵圆的面积S=πr2，
∴变量是S和r，常量是π，用S表示r为r=，
故说法错误的是B．
故选B．
　
2．分析: 在坐标系中，对于x的取值范围内的任意一点，通过这点作x轴的垂线，则垂线与图形只有一个交点．根据定义即可判断．
解：显然A、C、D三选项中，对于自变量x的任何值，y都有唯一的值与之相对应，y是x的函数；
B、对于x＞0的任何值，y都有二个值与之相对应，则y不是x的函数；
故选：B．
　
3．分析: 函数y=x中，自变量和函数值均可取任意实数，依次分析四个选项，自变量和函数值均可取任意实数的为正确答案．
解：A、x不能为0；
B、y不能为负数；
C、y不能为负数；
D、正确．
故本题选D．
　
4．分析: 利用二次根式的性质以及分数的性质分别得出关系式求出即可．
解：由题意可得：x+3≥0，x﹣5≠0，
解得：x≥﹣3且x≠5．
故选：D．
　
5．分析: 将x=﹣2代入y=，即可求出函数的解析式的值．
解：把x=﹣2代入y=得，
y==，
故选A．
　
6．分析: 根据题目提供的条件可以求出函数的解析式，根据解析式判断函数的图象的形状．
解：①x≤1时，两个三角形重叠面积为小三角形的面积，
∴y=×1×=，
②当1＜x≤2时，重叠三角形的边长为2﹣x，高为，
y=（2﹣x）×=x2﹣x+，
③当x=2时，两个三角形没有重叠的部分，即重叠面积为0，
故选：B．
　
7．分析: 根据正比例函数y=kx的定义条件是：k为常数且k≠0，自变量次数为1．
解；由正比例函数的定义可得：m2+2m≠0，m2﹣3=1，
解得；m=2．
故选A．
　
8．分析: 根据一次函数的定义条件进行逐一分析即可．
解：①y=2x+1是一次函数；
②y=自变量次数不为1，不是一次函数；
③y=﹣x是一次函数；
④s=60t是正比例函数，也是一次函数；
⑤y=100﹣25x是一次函数．
故选D．
　
9．分析: 分成四种情况分别进行讨论：①当m＞0，n＞0时；②当m＞0，n＜0时；③当m＜0，n＜0时；④当m＜0，n＞0时．21*cnjy*com
解：当m＞0，n＞0时，y1=mx+n的图象在第一、二、三象限，y2=nx+m的图象在第一、二、三象限，【来源：21cnj*y.co*m】
当m＞0，n＜0时，y1=mx+n的图象在第一、三、四象限，y2=nx+m的图象在第一、二、四象限，C选项符合；
当m＜0，n＜0时，y1=mx+n的图象在第二、三、四象限，y2=nx+m的图象在第三、二、四象限；
当m＜0，n＞0时，y1=mx+n的图象在第一、二、四象限，y2=nx+m的图象在第一、三、四象限；
故选：C．
　
10．分析: 先根据一次函数的解析式判断出函数的增减性，再比较出3与﹣2的大小，根据函数的增减性进行解答即可．
解：∵直线y=﹣2x+3中，k=﹣2＜0，
∴此函数中y随x的增大而减小，
∵3＞﹣2，
∴y1＜y2．
故选B．
　
11．分析: 根据平移可得直线y=2x+2沿y轴向下平移6个单位后解析式为y=2x+2﹣6=2x﹣4，再求出与x轴的交点即可．
解：直线y=2x+2沿y轴向下平移6个单位后解析式为y=2x+2﹣6=2x﹣4，
当y=0时，x=2，
因此与x轴的交点坐标是（2，0），
故选：D．
　
12．分析: 先求出一次函数y=kx+b与x轴和y轴的交点，再利用三角形的面积公式得到关于k的方程，解方程即可求出k的值．
解：∵一次函数y=kx+b（k≠0）图象过点（0，2），
∴b=2，
令y=0，则x=﹣，
∵函数图象与两坐标轴围成的三角形面积为2，
∴×2×|﹣|=2，即||=2，
解得：k=±1，
则函数的解析式是y=x+2或y=﹣x+2．
故选：C．
　
二．填空题（共8小题）
13．分析: 由一次函数y=（m+1）x﹣（4m﹣3）的图象不经过第三象限，则m+1＜0，并且﹣4m+3≥0，解两个不等式即可得到m的取值范围．
解：∵一次函数y=（m+1）x﹣（4m﹣3）的图象不经过第三象限，
∴m+1＜0，并且﹣4m+3≥0，
由m+1＜0，得m＜﹣1；由﹣4m+3≥0，得m≤﹣．
所以m的取值范围是m＜﹣1．
故答案为：m＜﹣1．
　
14．分析: 话费=三分钟以内的基本话费0.3+超过3分钟的时间×0.11，把相关数值代入即可求解．
解：超过3分钟的话费为0.11×（x﹣3），通话时间超过3分钟，
话费y（元）与通话时间x（x取整数，单位：分钟）之间的函数关系式为y=0.3+0.11x（x﹣3）=0.11x﹣0.03．
故答案为：y=0.11x﹣0.03．
　
15．分析: 根据式子特点，分x≤1，1＜x≤2，2＜x≤3，3＜x≤4，x＞4几种情况讨论．
解：①x≤1时，y=1﹣x+2（2﹣x）+3（3﹣x）+4（4﹣x）=30﹣10x，当x=1时，y最小值=30﹣10=20；
②1＜x≤2时，y=x﹣1+2（2﹣x）+3（3﹣x）+4（4﹣x）=﹣8x+28，当x=2时，y最小值=28﹣16=12；
③2＜x≤3时，y=x﹣1+2（x﹣2）+3（3﹣x）+4（4﹣x）=﹣4x+20，当x=3时，y最小值=20﹣12=8；
④3＜x≤4时，y=x﹣1+2（x﹣2）+3（x﹣3）+4（4﹣x）=2x+2，无最小值；
⑤x＞4时，y=x﹣1+2（x﹣2）+3（x﹣3）+4（x﹣4）=10x﹣30，无最小值．
综上所述，原式的最小值为8．
　
16．分析: 根据题意可得函数y=ax2+bx+c要变为一次函数必须a=0，且b≠0，因此m﹣2=0，且m≠0，再解即可．
解：根据题意可得：m﹣2=0，且m≠0，
解得：m=2，
故答案为：2．
　
17．分析: 根据一次函数是单调函数，因为知道函数定义域为﹣3≤x≤1，值域为1≤y≤9，进行分类讨论k大于0还是小于0，列出二元一次方程组求出k和b的值．
解：（Ⅰ）当k＞0时，，
解得：，
此时y=2x+7，
（Ⅱ）当k＜0时，，
解得：，
此时y=﹣2x+3，
综上，所求的函数解析式为：y=2x+7或y=﹣2x+3．
　
18．分析: ①根据函数图象由工作效率=工作总量÷工作时间就可以得出结论；
②根据函数图象由工作效率=工作总量÷工作时间就可以得出结论；
③根据函数图象求出乙队完成的时间就可以求出结论；
④由甲的工作效率就可以求出2天时的工作量为200米，乙队是300米．6天时甲队是600米，乙队是500米得出300﹣200=600﹣500=100米故得出结论．21教育网
解：①根据函数图象得：
甲队的工作效率为：600÷6=100米/天，故正确；
②根据函数图象，得
乙队开挖两天后的工作效率为：（500﹣300）÷（6﹣2）=50米/天，故正确；
③乙队完成任务的时间为：2+（600﹣300）÷50=8天，
∴甲队提前的时间为：8﹣6=2天．
∵2≠3，
∴③错误；
④当x=2时，甲队完成的工作量为：2×100=200米，
乙队完成的工作量为：300米．
当x=6时，甲队完成的工作量为600米，乙队完成的工作量为500米．
∵300﹣200=600﹣500=100，
∴当x=2或6时，甲乙两队所挖管道长度都相差100米．故正确．
故答案为：①②④．
　
19．分析: 依次求出S1、S2、…，即可发现规律：Sn=，最后计算s1+s2+s3+…+sn即可．
解：当n=1时，y=﹣x+，
此时，A（0，），B（，0），
∴S1=××=，
同理可得，S2=××=，
…
∴Sn=××=，
∴s1+s2+s3+…+sn=××…×=1﹣+﹣+…+﹣=1﹣=．
故答案为：
　
20．分析: 由图2可知，在点（10，40）至点（14，40）区间，△BPQ的面积不变，因此可推论BC=BE，由此分析动点P的运动过程如下：【来源：21·世纪·教育·网】
（1）在BE段，BP=BQ；持续时间10s，则BE=BC=10；y是t的二次函数；
（2）在ED段，y=40是定值，持续时间4s，则ED=4；
（3）在DC段，y持续减小直至为0，y是t的一次函数．
解：（1）分析函数图象可知，BC=10cm，ED=4cm，故AE=AD﹣ED=BC﹣ED=10﹣4=6cm，故①正确；
（2）如答图1所示，连接EC，过点E作EF⊥BC于点F，
由函数图象可知，BC=BE=10cm，S△BEC=40=BC?EF=×10×EF，∴EF=8，∴sin∠EBC=，故②正确；
（3）如答图2所示，过点P作PG⊥BQ于点G，
∵BQ=BP=t，
∴y=S△BPQ=BQ?PG=BQ?BP?sin∠EBC=t?t?=t2．
故③正确；
（4）结论D错误．理由如下：
当t=12s时，点Q与点C重合，点P运动到ED的中点，设为N，如答图3所示，连接NB，NC．
此时AN=8，ND=2，由勾股定理求得：NB=8，NC=2，
∵BC=10，
∴△BCN不是等腰三角形，即此时△PBQ不是等腰三角形．
故④错误；
故答案为：①②③．

　
三．解答题（共8小题）
21．分析: 利用一次函数的关系式画出函数图象，根据函数图象与坐标轴的交点及函数图象的性质解答即可．
解：依题意画出函数图象（如图）：
①从图象可以看到，直线y=2x+6与x轴的交点坐标为（﹣3，0），
∴方程2x+6=0
解得：x=﹣3．
②如图当x＞﹣3时，直线在x轴的上方，此时函数值大于0，
即：2x+6＞0．
∴所求不等式的解为：x＞﹣3；
③当﹣1≤y≤3，即﹣1≤2x+6≤3，
解得，﹣≤x≤﹣．
　
22．分析: （1）根据y﹣2与x+1成正比例关系设出函数的解析式，再把当x=﹣2时，y=6代入函数解析式即可求出k的值，进而求出y与x之间的函数解析式．
（2）根据（1）中所求函数解析式，将x=﹣3代入其中，求得y值；
（3）利用（1）中所求函数解析式，将y=4代入其中，求得x值．
解：（1）依题意得：设y﹣2=k（x+1）．
将x=﹣2，y=6代入：得k=﹣4
所以，y=﹣4x﹣2．
（2）由（1）知，y=﹣4x﹣2，
∴当x=﹣3时，y=（﹣4）×（﹣3）﹣2=10，即y=10；
（3）由（1）知，y=﹣4x﹣2，
∴当y=4时，4=（﹣4）×x﹣2，
解得，x=﹣．
　
23．分析: （1）根据一次函数的定义：一般地，形如y=kx+b（k≠0，k、b是常数）的函数，叫做一次函数，据此求解即可；【出处：21教育名师】
（2）根据正比例函数的定义：一般地，形如y=kx（k是常数，k≠0）的函数叫做正比例函数，其中k叫做比例系数，据此求解即可．
解：（1）根据一次函数的定义，得：2﹣|m|=1，
解得m=±1．
又∵m+1≠0即m≠﹣1，
∴当m=1，n为任意实数时，这个函数是一次函数；
（2）根据正比例函数的定义，得：2﹣|m|=1，n+4=0，
解得m=±1，n=﹣4，
又∵m+1≠0即m≠﹣1，
∴当m=1，n=﹣4时，这个函数是正比例函数．
　
24．分析: （1）利用等边三角形的性质得出OD=BD=1，再利用勾股定理得出AD的长，即可得出A点坐标，即可求出函数解析式；2·1·c·n·j·y
（2）利用E点坐标得出EO的长，进而求出AE的长，再利用勾股定理逆定理得出答案．
（1）解：过点A作AD⊥EO于点D，
∵△OAB是边长为2的等边三角形，
∴OD=DB=1，AB=AO=OB=2，
∴AD=，
∴A（1，），
将A点代入直线y=﹣x+m得：
=﹣+m，
解得：m=，
故y=﹣x+，
则y=0时，x=4，
即E（4，0）；
（2）证明：∵AD=，DE=EO﹣DO=3，
∴AE==2，
∵AO2+AE2=16，EO2=16，
∴AO2+AE2=EO2，
∴OA⊥AE．
　
25．分析: （1）根据和谐点的定义，利用矩形的面积和周长公式进行证明即可；
（2）利用和谐点的定义列出关于a的方程（a+3）×2=3a，由此可以求得a=6．然后把点P的坐标代入直线方程，通过方程来求b的值．【版权所有：21教育】
解：（1）∵1×2≠2（1+2），4×4=2×（4+4），
∴点M不是和谐点，点N是和谐点．
（2）由题意得，（a+3）×2=3a，
∴a=6，
∴P（6，3），
∵点P在直线y=﹣x+b上，
∴代入得3=﹣6+b，
解得，b=9．
综上所述，a、b的值分别是6，9．
　
26．（2008?武汉）（1）点（0，1）向下平移2个单位后的坐标是　（0，﹣1）　，直线y=2x+1向下平移2个单位后的解析式是　y=2x﹣1　；
（2）直线y=2x+1向右平移2个单位后的解析式是　y=2x﹣3　；
（3）如图，已知点C为直线y=x上在第一象限内一点，直线y=2x+1交y轴于点A，交x轴于B，将直线AB沿射线OC方向平移个单位，求平移后的直线的解析式．
分析: （1），（2）直接利用平移中点的变化规律求解即可．
（3）将直线AB沿射线OC方向平移个单位，其实是先向右平移3个单位长度，再向上平移3个单位长度．
解：（1）（0，﹣1），y=2x+1﹣2=2x﹣1；
（2）y=2（x﹣2）+1=2x﹣3；
（3）∵点C为直线y=x上在第一象限内一点，则直线上所有点的坐标横纵坐标相等，
∴将直线AB沿射线OC方向平移个单位，其实是先向右平移3个单位长度，再向上平移3个单位长度．
∴y=2（x﹣3）+1+3，即y=2x﹣2．
　
27．分析: （1）设每台A型电脑销售利润为x元，每台B型电脑的销售利润为y元，然后根据利润4000元和3500元列出方程组，然后求解即可；
（2）①根据总利润等于两种电脑的利润之和列式整理即可得解；
②根据B型电脑的进货量不超过A型电脑的2倍列不等式求出x的取值范围，然后根据一次函数的增减性求出利润的最大值即可．
解：（1）设每台A型电脑销售利润为x元，每台B型电脑的销售利润为y元，
根据题意得，
解得．
答：每台A型电脑销售利润为100元，每台B型电脑的销售利润为150元；
（2）①据题意得，y=100x+150（100﹣x），
即y=﹣50x+15000，
②据题意得，100﹣x≤2x，
解得x≥33，
∵y=﹣50x+15000，
∴y随x的增大而减小，
∵x为正整数，
∴当x=34时，y取最大值，则100﹣x=66，
即商店购进34台A型电脑和66台B型电脑的销售利润最大．
　
28．分析: （1）直接套用中点坐标公式，即可得出中点坐标；
（2）根据AC、BD的中点重合，可得出=，=，代入数据可得出点D的坐标；
（3）分类讨论，①当AB为该平行四边形一边时，此时CD∥AB，分别求出以AD、BC为对角线时，以AC、BD为对角线的情况可得出点D坐标；②当AB为该平行四边形的一条对角线时，根据AB中点与CD中点重合，可得出点D坐标．
解：（1）AB中点坐标为（，）=（1，1）；
（2）根据平行四边形的性质：对角线互相平分，可知AC、BD的中点重合，
由中点坐标公式可得：=，=，
代入数据，得：=，=，
解得：xD=6，yD=0，
所以点D的坐标为（6，0）．
（3）①当AB为该平行四边形一边时，则CD∥AB，对角线为AD、BC或AC、BD；
故可得：=，=或=，=，
故可得yC﹣yD=yA﹣yB=2或yD﹣yC=yA﹣yB=2
∵yC=0，
∴yD=2或﹣2，
代入到y=x+1中，可得D（2，2）或 D （﹣6，﹣2）．
当AB为该平行四边形的一条对角线时，则CD为另一条对角线；，
yC+yD=yA+yB=2+4，
∵yC=0，
∴yD=6，
代入到y=x+1中，可得D（10，6）
综上，符合条件的D点坐标为D（2，2）或 D（﹣6，﹣2）、D（10，6）．