19.2 一次函数 第5课时 一次函数的实际应用 同步练习
文档属性
| 名称 | 19.2 一次函数 第5课时 一次函数的实际应用 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 476.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-15 18:14:03 | ||
图片预览




文档简介
19.2 一次函数
第5课时 一次函数的实际应用
基础训练
知识点1建立一次函数模型解实际问题
1.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元),若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )21教育网
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡
2.一旅游团来到黄冈某旅游景点,看到售票处旁边的公告栏如图所示,请根据公告栏内容回答下列问题:
公告栏
各位游客,本景点门票价格如下:
(1)一次购买10张以下(含10张),每张门票180元;
(2)一次购买10张以上,超过10张的部分,每张门票6折优惠.
(1)若旅游团人数为9人,门票费用是 元;?
若旅游团人数为30人,门票费用是 元;?
(2)设旅游团人数为x人,写出该旅游团门票费用y(元)与人数x(人)的函数关系式(直接填写在下面的横线上).21·世纪*教育网
y=
3.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为元. 2-1-c-n-j-y
型号
A
B
单个盒子容量/升
2
3
单价/元
5
6
知识点2用一次函数解含图象的实际问题
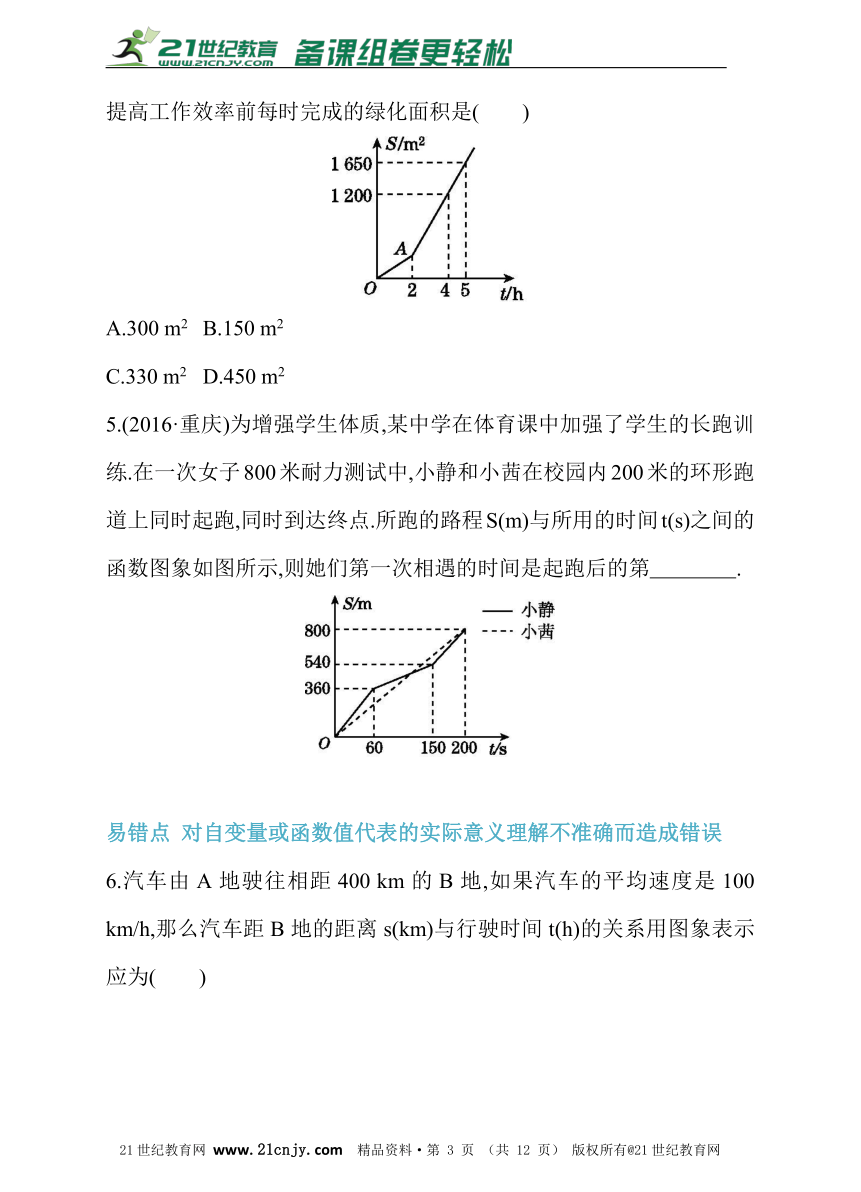
4.(2016·哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( )21*cnjy*com
A.300 m2 B.150 m2
C.330 m2 D.450 m2
5.(2016·重庆)为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点.所跑的路程S(m)与所用的时间t(s)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 .?
易错点 对自变量或函数值代表的实际意义理解不准确而造成错误
6.汽车由A地驶往相距400 km的B地,如果汽车的平均速度是100 km/h,那么汽车距B地的距离s(km)与行驶时间t(h)的关系用图象表示应为( )【出处:21教育名师】
提升训练
考查角度1利用一次函数性质解实际中最小值问题
7.为绿化校园,某校计划购进A,B两种树苗,共21棵.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.【版权所有:21教育】
(1)y与x的函数关系式为: ;?
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
考查角度2利用函数图象信息求其解析式解实际问题
8.水龙头关闭不严会造成滴水,容器内盛水量w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图①的试验,并根据试验数据绘制出如图②的函数图象,结合图象解答下列问题.21教育名师原创作品
(1)容器内原有水多少升?
(2)求w与t之间的函数解析式,并计算在这种滴水状态下一天的滴水量是多少升?
探究培优
拔尖角度1利用一次函数的性质解实际中方案问题
9.南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1 000元,乙货船每艘运费1 200元. 21*cnjy*com
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式.
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
10.已知y+2与x成正比例,且当x=6时,y=1.
(1)求这个函数的解析式,并指出y是x的什么函数?
(2)当x的值从-3增大到3时,函数值y是如何变化的?
拔尖角度2利用函数图象信息解实际问题
11.(2016·绥化)周末,小芳骑自行车从家出发到野外郊游,从家出发0.5 h到达甲地,游玩一段时间后按原速前往乙地,小芳离家1 h 20 min后,妈妈驾车沿相同路线前往乙地,行驶10 min,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳的离家时间x(h)的函数图象.
(1)小芳骑车的速度为 ,H点坐标为 .?
(2)小芳从家出发多久后被妈妈追上?此时距家的路程多远?
(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分到达乙地?21cnjy.com
12.学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人,如图所示,请你结合这个规律,填写下表并回答问题:【来源:21cnj*y.co*m】
拼成一行的方桌数(x)
1
2
3
4
…
人数(y)
4
6
8
…
(1)写出y与x之间的函数解析式,并判断y是不是x的一次函数;
(2)若八年级(1)班有42人去阅览室看书,则需要多少张这样的方桌拼成一行?
参考答案
1.【答案】C
解:设一年内在该游泳馆游泳的次数为x,消费的钱数为y,记不购买会员年卡时消费的钱数为y1,根据题意得21世纪教育网版权所有
y1=30x,yA=50+25x,yB=200+20x,yC=400+15x,当45≤x≤55时,确定y的范围,进行比较即可得到答案.www.21-cn-jy.com
2.【答案】(1)1 620;3 960 (2)180x;108x+720
3.【答案】29
解:设购买A种型号盒子x个,购买盒子所需要费用为y元,
则购买B种盒子的个数为个,下面分两种情况讨论:
①当0≤x<3时,y=5x+×6=x+30,
因为k=1>0,
所以y随x的增大而增大,
所以当x=0时,y有最小值,最小值为30元;
②当x≥3时,y=5x+×6-4=26+x,
因为k=1>0,
所以y随x的增大而增大,
所以当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.
4.【答案】B
解:如图,根据待定系数法可求直线AB的解析式,再根据函数解析式求出当x=2时y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每时完成的绿化面积.www-2-1-cnjy-com
5.【答案】120 s
解:如图,设直线OA的解析式为y1=k1x,
代入A(200,800)的坐标得800=200k1,解得k1=4,
故直线OA的解析式为y1=4x.
设BC的解析式为y2=k2x+b,
由题意得
解得
∴BC的解析式为y2=2x+240.
当y1=y2时,4x=2x+240,解得x=120.
∴她们第一次相遇的时间是起跑后的第120 s.
6.【答案】C
解:本题中s并不是汽车行驶的路程,而是汽车距B地的距离,不能被思维定式所左右,要仔细弄清题目,理解题意.实际上s与t的函数关系式为s=400-100t,其中0≤t≤4,s是t的一次函数,故选C.21·cn·jy·com
7.解:(1)y=-20x+1 890
(2)因为购买B种树苗的数量少于A种树苗的数量,
所以x<21-x,解得:x<10.5.
又因为x≥1,
所以x的取值范围为:1≤x≤10,且x为整数.
因为y=-20x+1 890,k=-20<0,
所以y随x的增大而减小,
所以当x=10时,y有最小值,
最小值为-20×10+1 890=1 690,
所以使费用最省的方案是购买B种树苗10棵,A种树苗11棵,所需费用为1 690元.
8.解:(1)根据图象可知,t=0时,w=0.3,
即容器内原有水0.3 L;
(2)设w与t之间的函数解析式为w=kt+b,将(0,0.3),(1.5,0.9)代入,得b=0.3①,1.5k+b=0.9②,2·1·c·n·j·y
将①代入②得k=0.4,故w与t之间的函数解析式为w=0.4t+0.3;
由解析式可得,每小时滴水量为0.4 L,一天的滴水量为0.4×24=9.6(L),即在这种滴水状态下一天的滴水量是9.6 L.【来源:21·世纪·教育·网】
9.解:(1)根据题意得:y=1 000x+1 200(30-x)=36 000-200x.
(2)根据题意得
化简得
所以23≤x≤25,
因为x为整数,
所以x可取23,24,25,
方案一:安排甲货船23艘,则安排乙货船7艘,
运费y=36 000-200×23
=31 400(元);
方案二:安排甲货船24艘,则安排乙货船6艘,
运费y=36 000-200×24
=31 200(元);
方案三:安排甲货船25艘,则安排乙货船5艘,
运费y=36 000-200×25
=31 000(元);
经分析得方案三运费最低,为31 000元.
10.解:(1)设y+2=kx.
∴1+2=6k,k=,
∴y=x-2,y是x的一次函数.
(2)当x=-3时,y=-2=-;当x=3时,y=-2=-,即函数值y从-增大到-.
11.解:(1)20 km/h;
(2)设直线AB的解析式为y1=k1x+b1,
根据其经过点A(0,30),B(0.5,20)可得y1=-20x+30.
∵AB∥CD,
∴设直线CD的解析式为y2=-20x+b2.
将点C(1,20)的坐标代入得b2=40,
∴y2=-20x+40.
设直线EF的解析式为y3=k3x+b3,
将点E,H代入得k3=-60,b3=110.
∴y3=-60x+110.
解方程组得
∴点D的坐标为(1.75,5).
30-5=25(km),
答:小芳出发1.75 h后被妈妈追上,此时距家25 km远.
(3)将y=0代入直线CD的解析式得-20x+40=0,
解得x=2.
将y=0代入直线EF的解析式有-60x+110=0,
解得x=.
2-=(h)=10(min).
答:小芳比预计时间早10 min到达乙地.
12.解:表中填10.
(1)y=2x+2,y是x的一次函数.
(2)把y=42代入y=2x+2中,
得42=2x+2,
解得x=20.
答:需要20张这样的方桌拼成一行.
第5课时 一次函数的实际应用
基础训练
知识点1建立一次函数模型解实际问题
1.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元),若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )21教育网
A.购买A类会员年卡 B.购买B类会员年卡
C.购买C类会员年卡 D.不购买会员年卡
2.一旅游团来到黄冈某旅游景点,看到售票处旁边的公告栏如图所示,请根据公告栏内容回答下列问题:
公告栏
各位游客,本景点门票价格如下:
(1)一次购买10张以下(含10张),每张门票180元;
(2)一次购买10张以上,超过10张的部分,每张门票6折优惠.
(1)若旅游团人数为9人,门票费用是 元;?
若旅游团人数为30人,门票费用是 元;?
(2)设旅游团人数为x人,写出该旅游团门票费用y(元)与人数x(人)的函数关系式(直接填写在下面的横线上).21·世纪*教育网
y=
3.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为元. 2-1-c-n-j-y
型号
A
B
单个盒子容量/升
2
3
单价/元
5
6
知识点2用一次函数解含图象的实际问题
4.(2016·哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( )21*cnjy*com
A.300 m2 B.150 m2
C.330 m2 D.450 m2
5.(2016·重庆)为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点.所跑的路程S(m)与所用的时间t(s)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 .?
易错点 对自变量或函数值代表的实际意义理解不准确而造成错误
6.汽车由A地驶往相距400 km的B地,如果汽车的平均速度是100 km/h,那么汽车距B地的距离s(km)与行驶时间t(h)的关系用图象表示应为( )【出处:21教育名师】
提升训练
考查角度1利用一次函数性质解实际中最小值问题
7.为绿化校园,某校计划购进A,B两种树苗,共21棵.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.【版权所有:21教育】
(1)y与x的函数关系式为: ;?
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
考查角度2利用函数图象信息求其解析式解实际问题
8.水龙头关闭不严会造成滴水,容器内盛水量w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图①的试验,并根据试验数据绘制出如图②的函数图象,结合图象解答下列问题.21教育名师原创作品
(1)容器内原有水多少升?
(2)求w与t之间的函数解析式,并计算在这种滴水状态下一天的滴水量是多少升?
探究培优
拔尖角度1利用一次函数的性质解实际中方案问题
9.南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1 000元,乙货船每艘运费1 200元. 21*cnjy*com
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式.
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
10.已知y+2与x成正比例,且当x=6时,y=1.
(1)求这个函数的解析式,并指出y是x的什么函数?
(2)当x的值从-3增大到3时,函数值y是如何变化的?
拔尖角度2利用函数图象信息解实际问题
11.(2016·绥化)周末,小芳骑自行车从家出发到野外郊游,从家出发0.5 h到达甲地,游玩一段时间后按原速前往乙地,小芳离家1 h 20 min后,妈妈驾车沿相同路线前往乙地,行驶10 min,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳的离家时间x(h)的函数图象.
(1)小芳骑车的速度为 ,H点坐标为 .?
(2)小芳从家出发多久后被妈妈追上?此时距家的路程多远?
(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分到达乙地?21cnjy.com
12.学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人,如图所示,请你结合这个规律,填写下表并回答问题:【来源:21cnj*y.co*m】
拼成一行的方桌数(x)
1
2
3
4
…
人数(y)
4
6
8
…
(1)写出y与x之间的函数解析式,并判断y是不是x的一次函数;
(2)若八年级(1)班有42人去阅览室看书,则需要多少张这样的方桌拼成一行?
参考答案
1.【答案】C
解:设一年内在该游泳馆游泳的次数为x,消费的钱数为y,记不购买会员年卡时消费的钱数为y1,根据题意得21世纪教育网版权所有
y1=30x,yA=50+25x,yB=200+20x,yC=400+15x,当45≤x≤55时,确定y的范围,进行比较即可得到答案.www.21-cn-jy.com
2.【答案】(1)1 620;3 960 (2)180x;108x+720
3.【答案】29
解:设购买A种型号盒子x个,购买盒子所需要费用为y元,
则购买B种盒子的个数为个,下面分两种情况讨论:
①当0≤x<3时,y=5x+×6=x+30,
因为k=1>0,
所以y随x的增大而增大,
所以当x=0时,y有最小值,最小值为30元;
②当x≥3时,y=5x+×6-4=26+x,
因为k=1>0,
所以y随x的增大而增大,
所以当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.
4.【答案】B
解:如图,根据待定系数法可求直线AB的解析式,再根据函数解析式求出当x=2时y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每时完成的绿化面积.www-2-1-cnjy-com
5.【答案】120 s
解:如图,设直线OA的解析式为y1=k1x,
代入A(200,800)的坐标得800=200k1,解得k1=4,
故直线OA的解析式为y1=4x.
设BC的解析式为y2=k2x+b,
由题意得
解得
∴BC的解析式为y2=2x+240.
当y1=y2时,4x=2x+240,解得x=120.
∴她们第一次相遇的时间是起跑后的第120 s.
6.【答案】C
解:本题中s并不是汽车行驶的路程,而是汽车距B地的距离,不能被思维定式所左右,要仔细弄清题目,理解题意.实际上s与t的函数关系式为s=400-100t,其中0≤t≤4,s是t的一次函数,故选C.21·cn·jy·com
7.解:(1)y=-20x+1 890
(2)因为购买B种树苗的数量少于A种树苗的数量,
所以x<21-x,解得:x<10.5.
又因为x≥1,
所以x的取值范围为:1≤x≤10,且x为整数.
因为y=-20x+1 890,k=-20<0,
所以y随x的增大而减小,
所以当x=10时,y有最小值,
最小值为-20×10+1 890=1 690,
所以使费用最省的方案是购买B种树苗10棵,A种树苗11棵,所需费用为1 690元.
8.解:(1)根据图象可知,t=0时,w=0.3,
即容器内原有水0.3 L;
(2)设w与t之间的函数解析式为w=kt+b,将(0,0.3),(1.5,0.9)代入,得b=0.3①,1.5k+b=0.9②,2·1·c·n·j·y
将①代入②得k=0.4,故w与t之间的函数解析式为w=0.4t+0.3;
由解析式可得,每小时滴水量为0.4 L,一天的滴水量为0.4×24=9.6(L),即在这种滴水状态下一天的滴水量是9.6 L.【来源:21·世纪·教育·网】
9.解:(1)根据题意得:y=1 000x+1 200(30-x)=36 000-200x.
(2)根据题意得
化简得
所以23≤x≤25,
因为x为整数,
所以x可取23,24,25,
方案一:安排甲货船23艘,则安排乙货船7艘,
运费y=36 000-200×23
=31 400(元);
方案二:安排甲货船24艘,则安排乙货船6艘,
运费y=36 000-200×24
=31 200(元);
方案三:安排甲货船25艘,则安排乙货船5艘,
运费y=36 000-200×25
=31 000(元);
经分析得方案三运费最低,为31 000元.
10.解:(1)设y+2=kx.
∴1+2=6k,k=,
∴y=x-2,y是x的一次函数.
(2)当x=-3时,y=-2=-;当x=3时,y=-2=-,即函数值y从-增大到-.
11.解:(1)20 km/h;
(2)设直线AB的解析式为y1=k1x+b1,
根据其经过点A(0,30),B(0.5,20)可得y1=-20x+30.
∵AB∥CD,
∴设直线CD的解析式为y2=-20x+b2.
将点C(1,20)的坐标代入得b2=40,
∴y2=-20x+40.
设直线EF的解析式为y3=k3x+b3,
将点E,H代入得k3=-60,b3=110.
∴y3=-60x+110.
解方程组得
∴点D的坐标为(1.75,5).
30-5=25(km),
答:小芳出发1.75 h后被妈妈追上,此时距家25 km远.
(3)将y=0代入直线CD的解析式得-20x+40=0,
解得x=2.
将y=0代入直线EF的解析式有-60x+110=0,
解得x=.
2-=(h)=10(min).
答:小芳比预计时间早10 min到达乙地.
12.解:表中填10.
(1)y=2x+2,y是x的一次函数.
(2)把y=42代入y=2x+2中,
得42=2x+2,
解得x=20.
答:需要20张这样的方桌拼成一行.
