20.1 数据的集中趋势 第5课时 应用中位数、众数及平均数分析数据 同步练习
文档属性
| 名称 | 20.1 数据的集中趋势 第5课时 应用中位数、众数及平均数分析数据 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 465.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-15 00:00:00 | ||
图片预览



文档简介
20.1 数据的集中趋势
第5课时 应用中位数、众数及平均数分析数据
基础训练
知识点1 “三数”在统计数据中应用
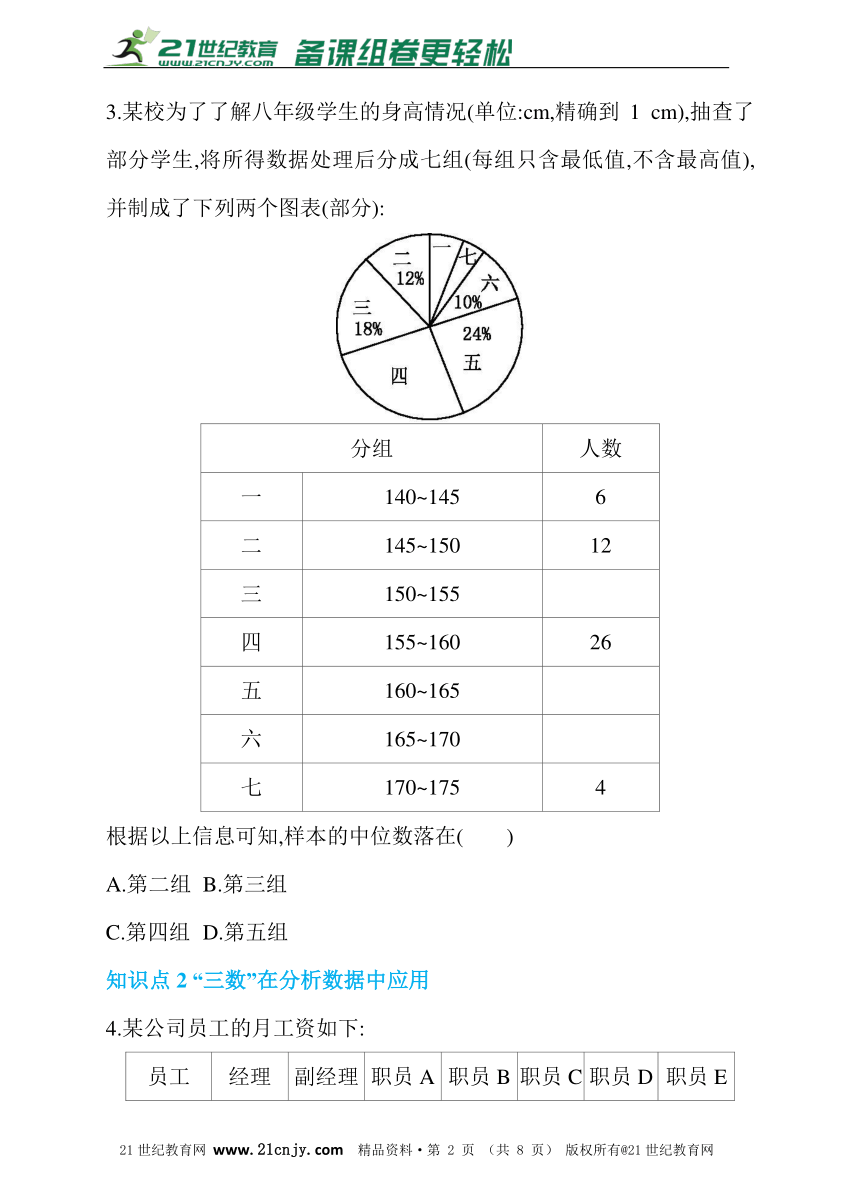
1.小红根据去年4~10月本班同学去孔子学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
/
A.46 B.42 C.32 D.27
2.(2016·西宁)赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
/
A.1.2万步,1.3万步 B.1.4万步,1.3万步
C.1.4万步,1.35万步 D.1.3万步,1.3万步
3.某校为了了解八年级学生的身高情况(单位:cm,精确到1 cm),抽查了部分学生,将所得数据处理后分成七组(每组只含最低值,不含最高值),并制成了下列两个图表(部分):
/
分组
人数
一
140~145
6
二
145~150
12
三
150~155
四
155~160
26
五
160~165
六
165~170
七
170~175
4
根据以上信息可知,样本的中位数落在( )
A.第二组 B.第三组
C.第四组 D.第五组
知识点2 “三数”在分析数据中应用
4.某公司员工的月工资如下:
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
月工资
/元
15 000
10 000
3 500
3 500
3 500
3 000
2 800
该公司员工月工资的中位数是________元,众数是________元,平均数
是________元.这三个量中,能够比较恰当地描述该公司员工月工资的一般水平的量是________.?
5.从甲、乙、丙三个厂家生产的同一种产品中,各抽出8件产品,对其使用寿命进行跟踪调查,结果如下(单位:年):
甲:3,4,5,6,8,8,8,10;
乙:4,6,6,6,8,9,12,13;
丙:3,3,4,7,9,10,11,12.
三个厂家在广告中都称该产品使用寿命为8年,根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一个反映集中趋势的特征量.
甲: ________,乙: ________,丙: ________.?
6.李华根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数
中位数
众数
8.5
8.3
8.1
如果要去掉一个最高分和一个最低分,那么表中数据一定不发生变化的是( )
A.平均数 B.众数
C.中位数 D.无法确定
易错点 不能正确选用参照数据而致错
7.某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取得前6名才能参加决赛.韩丽梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数
C.平均数 D.最大值和最小值
提升训练
考查角度1利用平均数、中位数分析数据
8.甲、乙两班参加“学数学用数学”知识竞赛,两班的参赛人数相等,比赛结束后,依据两班学生成绩绘制了统计表和统计图(如图).
乙班学生“学数学用数学”知识竞赛成绩统计表
分数
6分
7分
8分
9分
人数
1
10
3
6
(1)经计算乙班学生的平均成绩为7.7分,中位数为7分.请计算甲班学生的平均成绩、中位数,并从平均数和中位数的角度分析哪个班的成绩较好.
(2)如果学校决定要组织6个人的代表队参加校级邀请赛,为了便于管理,决定依据本次比赛成绩,只在这两个班的其中一个班中挑选参赛选手,你认为应在哪个班选?请说明理由.
/
考查角度2利用中位数、众数分析数据
9.在对全市初中生进行的体质健康测试中,青少年体质研究中心随机抽取的10名学生的坐位体前屈的成绩(单位:厘米)如下:
11.2,10.5,11.4,10.2,11.4,11.4,11.2,9.5,12.0,10.2
(1)通过计算,样本数据(10名学生的成绩)的平均数是10.9,中位数是________,众数是________;?
(2)一名学生的成绩是11.3厘米,你认为他的成绩如何?说明理由.
(3)研究中心确定了一个标准成绩,等于或大于这个成绩的学生该项素质被评定为“优秀”等级,如果全市有一半左右的学生能够达到“优秀”等级,你认为标准成绩定为多少?说明理由.
探究培优
拔尖角度 利用平均数、中位数、众数分析数据
10.(2016·天津)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下所示的统计图,请根据相关信息,解答下列问题:
/
(1)图①中a的值为_________;?
(2)求统计的这组初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请判断初赛成绩为1.65 m的运动员能否进入复赛.
参考答案
1.【答案】C
2.【答案】B
解:由条形统计图中出现频数最大(即条形最高)的数据是在第四组,故众数是1.4万步,因为图中是按从小到大的顺序排列的,最中间的步数都是1.3万步,所以中位数是1.3万步.
故选B.
3.【答案】C
解:结合扇形统计图可知第三、五、六组的人数分别为18,24,10,且样本容量为100,所以中位数是第50和第51个数的平均数,显然这两个数都落在第四组,因此样本的中位数也落在第四组.
4.【答案】3 500;3 500;5 900;众数或中位数
5.【答案】众数;平均数;中位数
6.【答案】C
7.【答案】A
解:由于中位数就是一组数据(奇数个)按照从小到大(或从大到小)的顺序排列后处于中间位置的那个数,因此分析能否进入决赛可以参考中位数.若她的成绩比中位数大,则能进入决赛;若她的成绩比中位数小,则不能进入决赛.故选A.
8.解:(1)由甲、乙两班参赛人数相等知,甲班为20人.得6分人数:20×25%=5(人),得7分人数:20×20%=4(人),得8分人数:20×35%=7(人),得9分人数:20×20%=4(人).甲班学生的平均成绩为(6×5+7×4+8×7+9×4)÷20=7.5(分),中位数为8分.
从平均数看,乙班成绩较好;从中位数看,甲班成绩较好.
(2)应在乙班选.
因为乙班有6人得9分,而甲班只有4人得9分,所以应在乙班选.
9.解:(1)11.2;11.4
(2)他的成绩比一半以上学生的成绩好,理由如下:根据(1)中得到的样本数据的结论,可以估计在这次坐位体前屈的测试成绩中,全市大约有一半学生的成绩大于11.2厘米,有一半学生的成绩小于11.2厘米,这名学生的成绩是11.3厘米,大于中位数(11.2厘米),可以推测他的成绩比一半以上学生的成绩好(答案不唯一,合理即可).
(3)如果全市有一半左右的学生能够达到“优秀”等级,那么标准成绩应定为11.2厘米(中位数),因为从样本情况看,成绩在11.2厘米以上(含11.2厘米)的学生占总人数的一半左右,可以估计,如果标准成绩定为11.2厘米,全市将有一半左右的学生能够达到“优秀”等级.
10.解:(1)25
(2)观察条形统计图得
??
=
1.50×2+1.55×4+1.60×5+1.65×6+1.70×3
2+4+5+6+3
=1.61(m),
∴这组数据的平均数为1.61 m.
∵在这组数据中,1.65 m出现了6次,出现的次数最多,
∴这组数据的众数是1.65 m.
将这组数据从小到大排列,其中处于中间的两个数都是1.60 m,
∴这组数据的中位数是1.60 m.
(3)∵共有20个人,中位数是第10,11个数的平均数,
∴根据中位数可以判断出能否进入前9名.
∵1.65 m>1.60 m,∴能进入复赛.
第5课时 应用中位数、众数及平均数分析数据
基础训练
知识点1 “三数”在统计数据中应用
1.小红根据去年4~10月本班同学去孔子学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
/
A.46 B.42 C.32 D.27
2.(2016·西宁)赵老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
/
A.1.2万步,1.3万步 B.1.4万步,1.3万步
C.1.4万步,1.35万步 D.1.3万步,1.3万步
3.某校为了了解八年级学生的身高情况(单位:cm,精确到1 cm),抽查了部分学生,将所得数据处理后分成七组(每组只含最低值,不含最高值),并制成了下列两个图表(部分):
/
分组
人数
一
140~145
6
二
145~150
12
三
150~155
四
155~160
26
五
160~165
六
165~170
七
170~175
4
根据以上信息可知,样本的中位数落在( )
A.第二组 B.第三组
C.第四组 D.第五组
知识点2 “三数”在分析数据中应用
4.某公司员工的月工资如下:
员工
经理
副经理
职员A
职员B
职员C
职员D
职员E
月工资
/元
15 000
10 000
3 500
3 500
3 500
3 000
2 800
该公司员工月工资的中位数是________元,众数是________元,平均数
是________元.这三个量中,能够比较恰当地描述该公司员工月工资的一般水平的量是________.?
5.从甲、乙、丙三个厂家生产的同一种产品中,各抽出8件产品,对其使用寿命进行跟踪调查,结果如下(单位:年):
甲:3,4,5,6,8,8,8,10;
乙:4,6,6,6,8,9,12,13;
丙:3,3,4,7,9,10,11,12.
三个厂家在广告中都称该产品使用寿命为8年,根据调查结果判断厂家在广告中分别运用了平均数、众数、中位数中哪一个反映集中趋势的特征量.
甲: ________,乙: ________,丙: ________.?
6.李华根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数
中位数
众数
8.5
8.3
8.1
如果要去掉一个最高分和一个最低分,那么表中数据一定不发生变化的是( )
A.平均数 B.众数
C.中位数 D.无法确定
易错点 不能正确选用参照数据而致错
7.某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取得前6名才能参加决赛.韩丽梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数
C.平均数 D.最大值和最小值
提升训练
考查角度1利用平均数、中位数分析数据
8.甲、乙两班参加“学数学用数学”知识竞赛,两班的参赛人数相等,比赛结束后,依据两班学生成绩绘制了统计表和统计图(如图).
乙班学生“学数学用数学”知识竞赛成绩统计表
分数
6分
7分
8分
9分
人数
1
10
3
6
(1)经计算乙班学生的平均成绩为7.7分,中位数为7分.请计算甲班学生的平均成绩、中位数,并从平均数和中位数的角度分析哪个班的成绩较好.
(2)如果学校决定要组织6个人的代表队参加校级邀请赛,为了便于管理,决定依据本次比赛成绩,只在这两个班的其中一个班中挑选参赛选手,你认为应在哪个班选?请说明理由.
/
考查角度2利用中位数、众数分析数据
9.在对全市初中生进行的体质健康测试中,青少年体质研究中心随机抽取的10名学生的坐位体前屈的成绩(单位:厘米)如下:
11.2,10.5,11.4,10.2,11.4,11.4,11.2,9.5,12.0,10.2
(1)通过计算,样本数据(10名学生的成绩)的平均数是10.9,中位数是________,众数是________;?
(2)一名学生的成绩是11.3厘米,你认为他的成绩如何?说明理由.
(3)研究中心确定了一个标准成绩,等于或大于这个成绩的学生该项素质被评定为“优秀”等级,如果全市有一半左右的学生能够达到“优秀”等级,你认为标准成绩定为多少?说明理由.
探究培优
拔尖角度 利用平均数、中位数、众数分析数据
10.(2016·天津)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下所示的统计图,请根据相关信息,解答下列问题:
/
(1)图①中a的值为_________;?
(2)求统计的这组初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请判断初赛成绩为1.65 m的运动员能否进入复赛.
参考答案
1.【答案】C
2.【答案】B
解:由条形统计图中出现频数最大(即条形最高)的数据是在第四组,故众数是1.4万步,因为图中是按从小到大的顺序排列的,最中间的步数都是1.3万步,所以中位数是1.3万步.
故选B.
3.【答案】C
解:结合扇形统计图可知第三、五、六组的人数分别为18,24,10,且样本容量为100,所以中位数是第50和第51个数的平均数,显然这两个数都落在第四组,因此样本的中位数也落在第四组.
4.【答案】3 500;3 500;5 900;众数或中位数
5.【答案】众数;平均数;中位数
6.【答案】C
7.【答案】A
解:由于中位数就是一组数据(奇数个)按照从小到大(或从大到小)的顺序排列后处于中间位置的那个数,因此分析能否进入决赛可以参考中位数.若她的成绩比中位数大,则能进入决赛;若她的成绩比中位数小,则不能进入决赛.故选A.
8.解:(1)由甲、乙两班参赛人数相等知,甲班为20人.得6分人数:20×25%=5(人),得7分人数:20×20%=4(人),得8分人数:20×35%=7(人),得9分人数:20×20%=4(人).甲班学生的平均成绩为(6×5+7×4+8×7+9×4)÷20=7.5(分),中位数为8分.
从平均数看,乙班成绩较好;从中位数看,甲班成绩较好.
(2)应在乙班选.
因为乙班有6人得9分,而甲班只有4人得9分,所以应在乙班选.
9.解:(1)11.2;11.4
(2)他的成绩比一半以上学生的成绩好,理由如下:根据(1)中得到的样本数据的结论,可以估计在这次坐位体前屈的测试成绩中,全市大约有一半学生的成绩大于11.2厘米,有一半学生的成绩小于11.2厘米,这名学生的成绩是11.3厘米,大于中位数(11.2厘米),可以推测他的成绩比一半以上学生的成绩好(答案不唯一,合理即可).
(3)如果全市有一半左右的学生能够达到“优秀”等级,那么标准成绩应定为11.2厘米(中位数),因为从样本情况看,成绩在11.2厘米以上(含11.2厘米)的学生占总人数的一半左右,可以估计,如果标准成绩定为11.2厘米,全市将有一半左右的学生能够达到“优秀”等级.
10.解:(1)25
(2)观察条形统计图得
??
=
1.50×2+1.55×4+1.60×5+1.65×6+1.70×3
2+4+5+6+3
=1.61(m),
∴这组数据的平均数为1.61 m.
∵在这组数据中,1.65 m出现了6次,出现的次数最多,
∴这组数据的众数是1.65 m.
将这组数据从小到大排列,其中处于中间的两个数都是1.60 m,
∴这组数据的中位数是1.60 m.
(3)∵共有20个人,中位数是第10,11个数的平均数,
∴根据中位数可以判断出能否进入前9名.
∵1.65 m>1.60 m,∴能进入复赛.
