5.1 相交线 第3课时 垂线段 同步练习
文档属性
| 名称 | 5.1 相交线 第3课时 垂线段 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 477.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 15:18:40 | ||
图片预览



文档简介
5.1 相交线
第3课时 垂线段
基础训练
知识点1 垂线段的定义
1.下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直线相交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段
2.如图,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB
B.点C到AB的垂线段是线段AC
C.线段AC是点A到BC的垂线段
D.线段BD是点B到AD的垂线段
知识点2 垂线段的性质
3.如图,计划在河边建一水厂,过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是__________.?
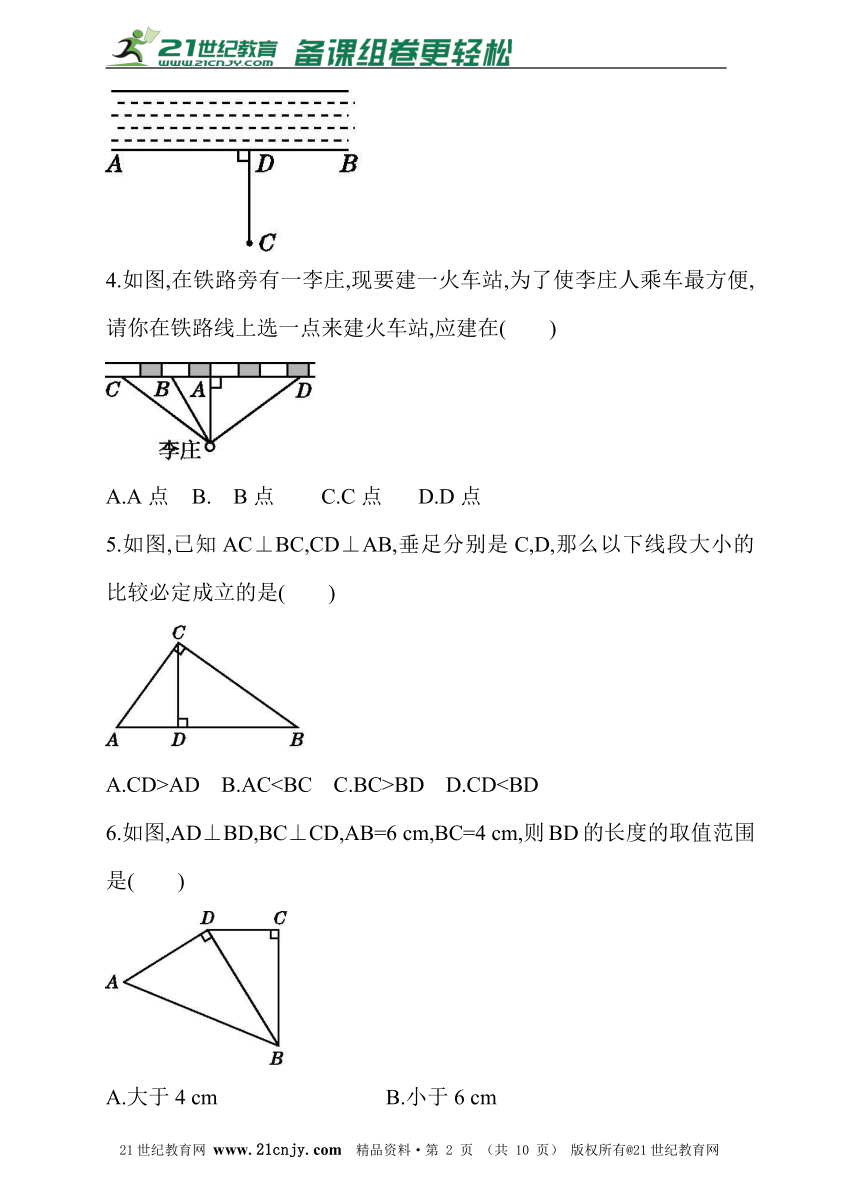
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )21世纪教育网版权所有
A.A点 B. B点 C.C点 D.D点
5.如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.CD>AD B.ACBD D.CD6.如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,则BD的长度的取值范围是( )
A.大于4 cm B.小于6 cm
C.大于4 cm或小于 6 cm D.大于 4 cm且小于 6 cm
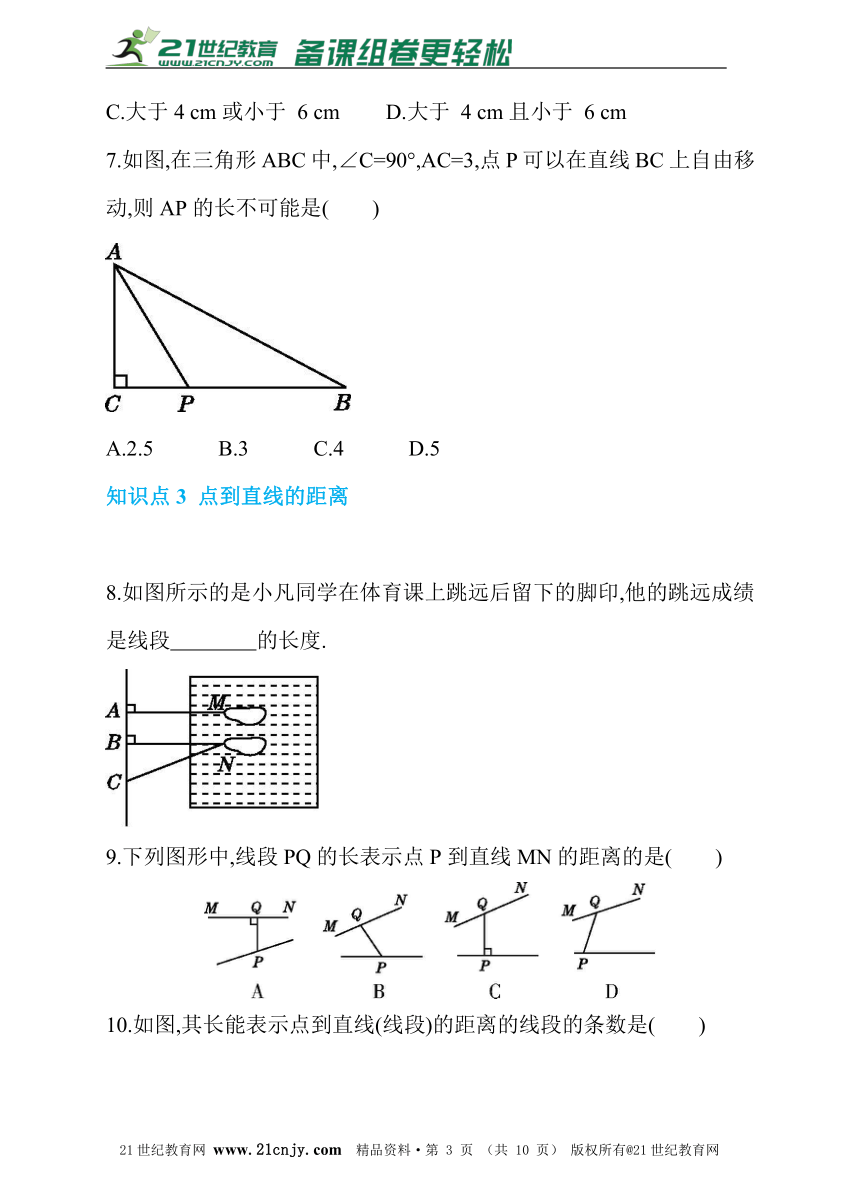
7.如图,在三角形ABC中,∠C=90°,AC=3,点P可以在直线BC上自由移动,则AP的长不可能是( )www-2-1-cnjy-com
A.2.5 B.3 C.4 D.5
知识点3 点到直线的距离
8.如图所示的是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.?
9.下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
10.如图,其长能表示点到直线(线段)的距离的线段的条数是( )
A.3 B.4 C.5 D.6
11.如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )21教育网
A.线段CA的长 B.线段CD的长
C.线段AD的长 D.线段AB的长
12.点到直线的距离是指( )
A.直线外一点到这条直线的垂线的长度
B.直线外一点到这条直线上的任意一点的距离
C.直线外一点到这条直线的垂线段
D.直线外一点到这条直线的垂线段的长度
13.如图,AB⊥AC,AD⊥BC,如果AB=4 cm,AC=3 cm,AD=2.4 cm,那么点C到直线AB的距离为( )21cnjy.com
A.3 cm B.4 cm C.2.4 cm D.无法确定
易错点 对垂线段的性质理解不透彻而致错
14.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )2-1-c-n-j-y
A.等于4 cm B.等于2 cm
C.小于2 cm D.不大于2 cm
提升训练
考查角度1 利用点到直线的距离的定义进行识别
15.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
考查角度2 利用作垂线法作图
16.如图,已知钝角三角形ABC中,∠BAC为钝角.
(1)画出点C到AB的垂线段;
(2)过点A画BC的垂线;
(3)画出点B到AC的垂线段,并量出其长度.
考查角度3 利用垂线段的性质比较大小
17.如图,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线段PE;
(2)过点P画CD的垂线,与AB相交于F点;
(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?
考查角度4 利用垂线段的性质解实际应用题
18.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到点P位置时,离村庄M最近,行驶到点Q位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
探究培优
拔尖角度1 利用垂线段的性质进行方案设计(建模思想)
19.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.
拔尖角度2 利用垂线段的性质解决绝对值问题(数形结合思想)
20.在如图所示的直角三角形ABC中,斜边为BC,两直角边分别为AB,AC,设BC=a,AC=b,AB=c.21·世纪*教育网
(1)试用所学知识说明斜边BC是最长的边;
(2)试化简|a-b|+|c-a|+|b+c-a|.
参考答案
1.【答案】D 2.【答案】C
3.【答案】垂线段最短
4.【答案】A 5.【答案】C
6.【答案】D
解:根据“垂线段最短”可知BC7.【答案】A
8.【答案】BN或AM
9.【答案】A
解:对于选项A,PQ⊥MN,Q是垂足,故线段PQ的长为点P到直线MN的距离.
10.【答案】C
解:线段AB的长度可表示点B到AC的距离,线段CA的长度可表示点C到AB的距离,线段AD的长度可表示点A到BC的距离,线段CD的长度可表示点C到AD的距离,线段BD的长度可表示点B到AD的距离,所以共有5条.21·cn·jy·com
11.【答案】B 12.【答案】D
13.【答案】A
解:因为AB⊥AC,所以点C到直线AB的距离是线段AC的长度,即3 cm.
14.错解:B
诊断:点到直线的距离是指这个点到直线的垂线段的长度.虽然垂线段最短,但是并没有说明PC是垂线段,所以垂线段的长度可能小于2 cm,也可能等于2 cm.www.21-cn-jy.com
正解:D
15.【答案】D
16.解:如图:(1)CD即为所求;(2)直线AE即为所求;(3)BF即为所求.长度略.
17.解:(1)如图所示. (2)如图所示.
(3)PE18.解:如图所示.
19.解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池的位置,它到四个村庄的距离之和最小.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开渠最短.根据:连接直线外一点与直线上各点的所有线段中,垂线段最短.2·1·c·n·j·y
分析:本题考查了垂线段的性质在实际生活中的运用.体现了建模思想的运用.
20.解:(1)因为点C与直线AB上点A,B的连线中,CA是垂线段,所以AC(2)因为BC>AC,ABBC,所以原式=a-b-(c-a)+b+c-a=a.
第3课时 垂线段
基础训练
知识点1 垂线段的定义
1.下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直线相交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段
2.如图,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB
B.点C到AB的垂线段是线段AC
C.线段AC是点A到BC的垂线段
D.线段BD是点B到AD的垂线段
知识点2 垂线段的性质
3.如图,计划在河边建一水厂,过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是__________.?
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )21世纪教育网版权所有
A.A点 B. B点 C.C点 D.D点
5.如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.CD>AD B.AC
A.大于4 cm B.小于6 cm
C.大于4 cm或小于 6 cm D.大于 4 cm且小于 6 cm
7.如图,在三角形ABC中,∠C=90°,AC=3,点P可以在直线BC上自由移动,则AP的长不可能是( )www-2-1-cnjy-com
A.2.5 B.3 C.4 D.5
知识点3 点到直线的距离
8.如图所示的是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.?
9.下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
10.如图,其长能表示点到直线(线段)的距离的线段的条数是( )
A.3 B.4 C.5 D.6
11.如图,三角形ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )21教育网
A.线段CA的长 B.线段CD的长
C.线段AD的长 D.线段AB的长
12.点到直线的距离是指( )
A.直线外一点到这条直线的垂线的长度
B.直线外一点到这条直线上的任意一点的距离
C.直线外一点到这条直线的垂线段
D.直线外一点到这条直线的垂线段的长度
13.如图,AB⊥AC,AD⊥BC,如果AB=4 cm,AC=3 cm,AD=2.4 cm,那么点C到直线AB的距离为( )21cnjy.com
A.3 cm B.4 cm C.2.4 cm D.无法确定
易错点 对垂线段的性质理解不透彻而致错
14.点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )2-1-c-n-j-y
A.等于4 cm B.等于2 cm
C.小于2 cm D.不大于2 cm
提升训练
考查角度1 利用点到直线的距离的定义进行识别
15.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
考查角度2 利用作垂线法作图
16.如图,已知钝角三角形ABC中,∠BAC为钝角.
(1)画出点C到AB的垂线段;
(2)过点A画BC的垂线;
(3)画出点B到AC的垂线段,并量出其长度.
考查角度3 利用垂线段的性质比较大小
17.如图,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线段PE;
(2)过点P画CD的垂线,与AB相交于F点;
(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?
考查角度4 利用垂线段的性质解实际应用题
18.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到点P位置时,离村庄M最近,行驶到点Q位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
探究培优
拔尖角度1 利用垂线段的性质进行方案设计(建模思想)
19.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.
拔尖角度2 利用垂线段的性质解决绝对值问题(数形结合思想)
20.在如图所示的直角三角形ABC中,斜边为BC,两直角边分别为AB,AC,设BC=a,AC=b,AB=c.21·世纪*教育网
(1)试用所学知识说明斜边BC是最长的边;
(2)试化简|a-b|+|c-a|+|b+c-a|.
参考答案
1.【答案】D 2.【答案】C
3.【答案】垂线段最短
4.【答案】A 5.【答案】C
6.【答案】D
解:根据“垂线段最短”可知BC
8.【答案】BN或AM
9.【答案】A
解:对于选项A,PQ⊥MN,Q是垂足,故线段PQ的长为点P到直线MN的距离.
10.【答案】C
解:线段AB的长度可表示点B到AC的距离,线段CA的长度可表示点C到AB的距离,线段AD的长度可表示点A到BC的距离,线段CD的长度可表示点C到AD的距离,线段BD的长度可表示点B到AD的距离,所以共有5条.21·cn·jy·com
11.【答案】B 12.【答案】D
13.【答案】A
解:因为AB⊥AC,所以点C到直线AB的距离是线段AC的长度,即3 cm.
14.错解:B
诊断:点到直线的距离是指这个点到直线的垂线段的长度.虽然垂线段最短,但是并没有说明PC是垂线段,所以垂线段的长度可能小于2 cm,也可能等于2 cm.www.21-cn-jy.com
正解:D
15.【答案】D
16.解:如图:(1)CD即为所求;(2)直线AE即为所求;(3)BF即为所求.长度略.
17.解:(1)如图所示. (2)如图所示.
(3)PE
19.解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池的位置,它到四个村庄的距离之和最小.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开渠最短.根据:连接直线外一点与直线上各点的所有线段中,垂线段最短.2·1·c·n·j·y
分析:本题考查了垂线段的性质在实际生活中的运用.体现了建模思想的运用.
20.解:(1)因为点C与直线AB上点A,B的连线中,CA是垂线段,所以AC
