1.1 等腰三角形 同步练习(含答案)
文档属性
| 名称 | 1.1 等腰三角形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 202.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 18:41:59 | ||
图片预览


文档简介
1.1等腰三角形
同步练习
一、单选题
1、下列说法错误的是(
)
A、等腰三角形两腰上的中线相等
B、等腰三角形两腰上的高线相等
C、等腰三角形的中线与高重合
D、等腰三角形底边的中线上任一点到两腰的距离相等
2、如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、
F,则下列四个结论中,①AB上有一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相
等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是( )
A、1个
B、2
个
C、3
个
D、4个
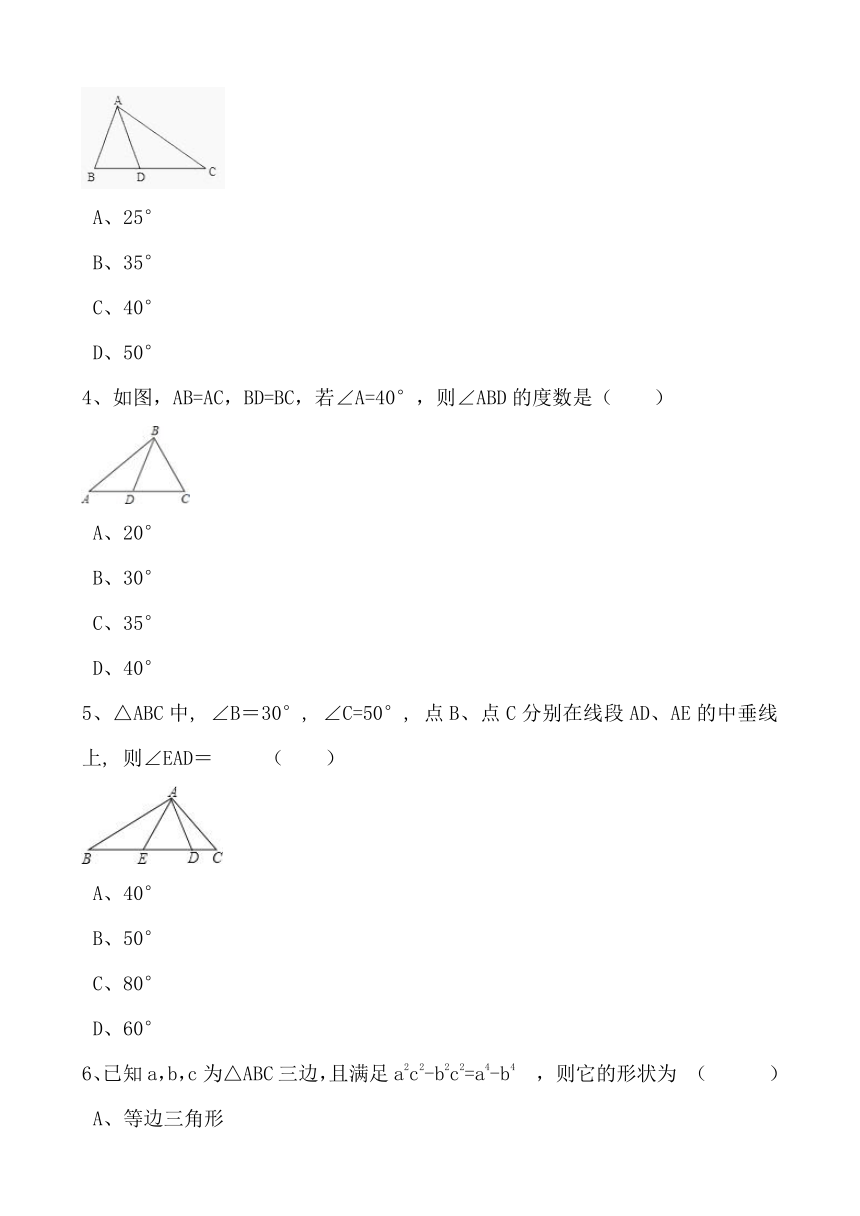
3、如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C为 ( ).
A、25°
B、35°
C、40°
D、50°
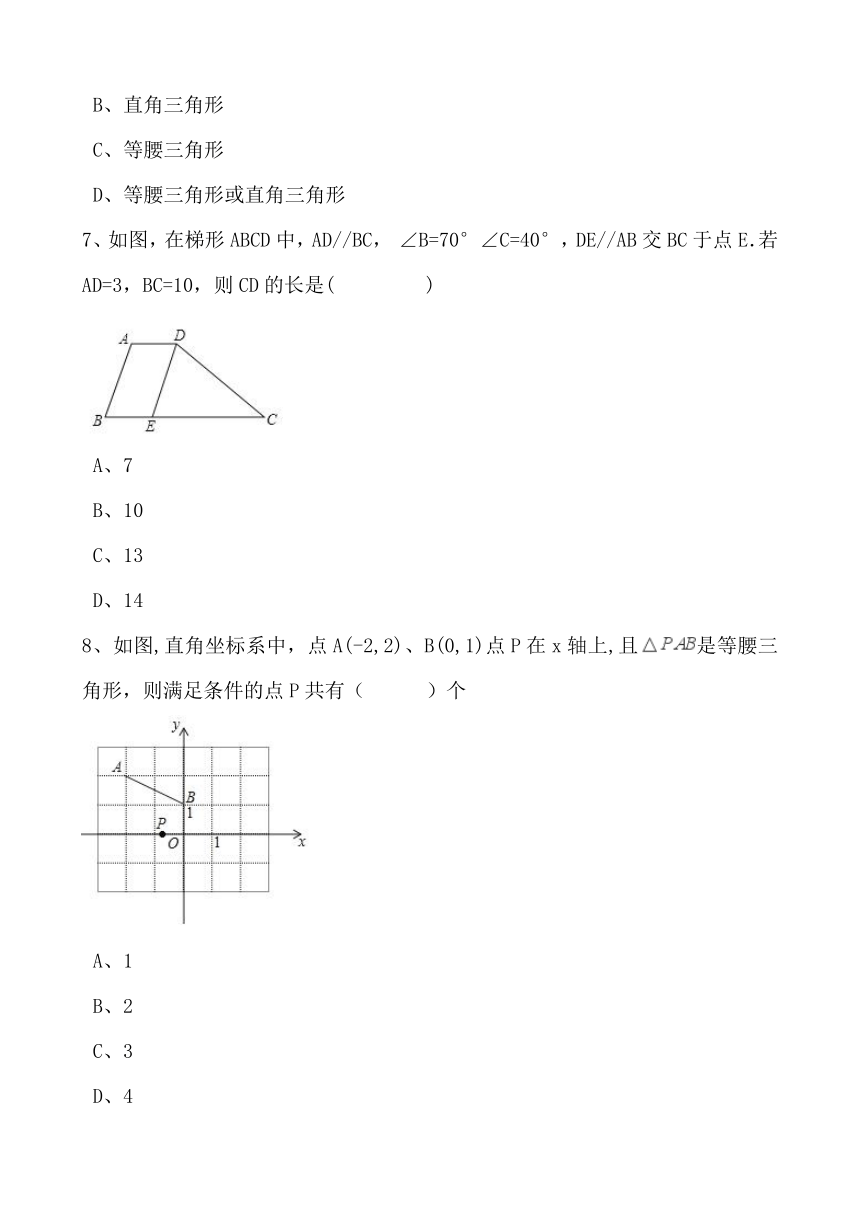
4、如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
A、20°
B、30°
C、35°
D、40°
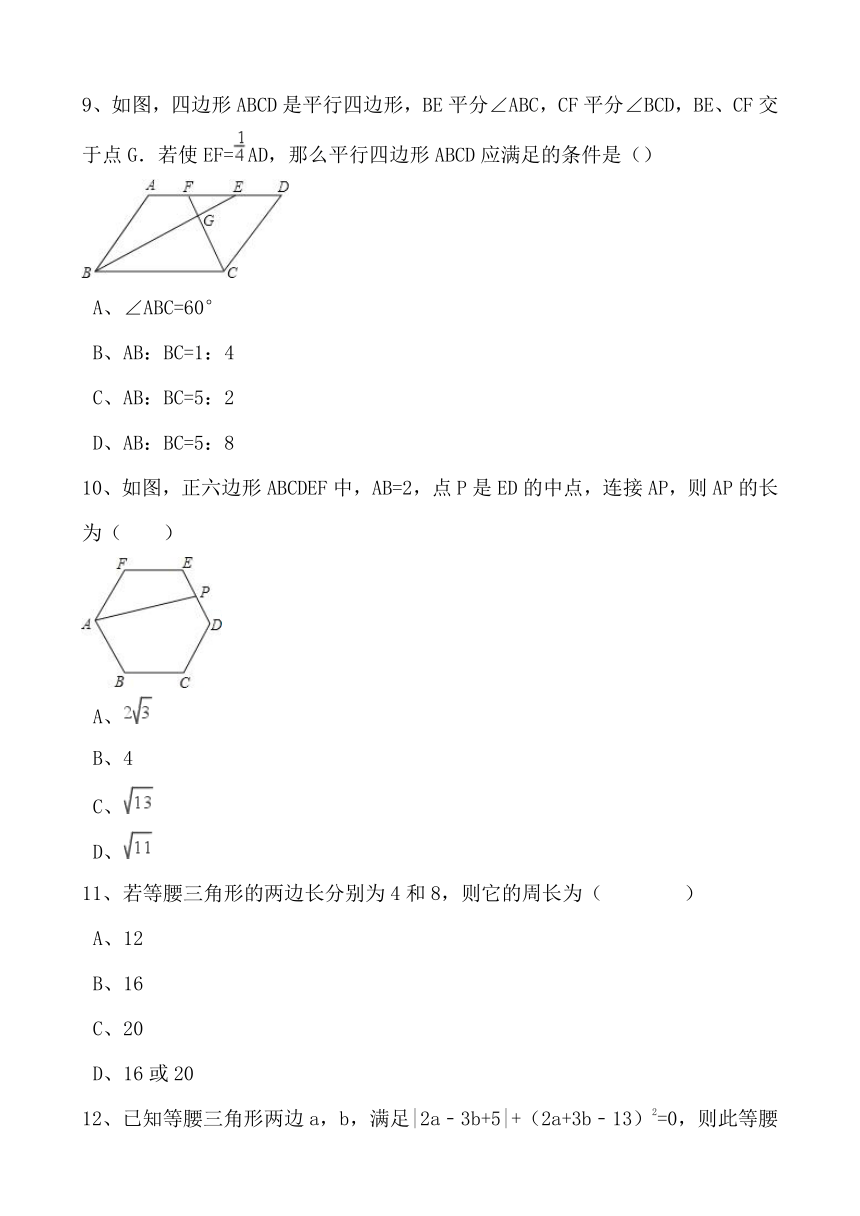
5、△ABC中,
∠B=30°,
∠C=50°,
点B、点C分别在线段AD、AE的中垂线上,
则∠EAD=
( )
A、40°
B、50°
C、80°
D、60°
6、已知a,b,c为△ABC三边,且满足a2c2-b2c2=a4-b4
,
则它的形状为 ( )
A、等边三角形
B、直角三角形
C、等腰三角形
D、等腰三角形或直角三角形
7、如图,在梯形ABCD中,AD//BC,
∠B=70°∠C=40°,DE//AB交BC于点E.若AD=3,BC=10,则CD的长是(
)
A、7
B、10
C、13
D、14
8、如图,直角坐标系中,点A(-2,2)、B(0,1)点P在x轴上,且是等腰三角形,则满足条件的点P共有( )个
A、1
B、2
C、3
D、4
9、如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF=AD,那么平行四边形ABCD应满足的条件是()
A、∠ABC=60°
B、AB:BC=1:4
C、AB:BC=5:2
D、AB:BC=5:8
10、如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( )
A、
B、4
C、
D、
11、若等腰三角形的两边长分别为4和8,则它的周长为( )
A、12
B、16
C、20
D、16或20
12、已知等腰三角形两边a,b,满足|2a﹣3b+5|+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
A、7或8
B、6或10
C、6或7
D、7或10
13、一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米( )
A、50
B、50或40
C、50或40或30
D、50或30或20
14、在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
A、②③
B、③④
C、①②④
D、②③④
15、如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1
,
P2
,
…P10
,
记Mi=APi2+PiB PiC(i=1,2,…,10),那么M1+M2+…+M10的值为( )
A、4
B、14
C、40
D、不能确定
二、填空题
16、如图,∠A
=∠D
,
OA=OD,
∠DOC=50°,则∠DBC=________度.
17、如图∠AOP=∠BOP=15°,PC∥OA
,
PD⊥OA
,
若PC=6,则PD等于________.
18、若等腰三角形的两边分别是一元二次方程x2﹣12x+32=0的两根,则等腰三角形的周长为________ .
19、如图4所示,在△ABC中,AB=AC
,
D为BC的中点,则△ABD≌△ACD
,
根据是________ ,AD与BC的位置关系是________ .
20、△ABC中,∠A=90°,AB=AC
,
BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第________张.
三、解答题
21、已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,求三角形ABC的周长
22、一如图,在△ABC中,AB=41cm,BC=18cm,BC边上的中线AD=40cm.△ABC是等腰三角形吗?为什么?
23、如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
24、如图一次函数的图象分别交x轴、y轴于点A,B,与反比例函数图象在第二象限交于点C(m,6),轴于点D,OA=OD.
(1)求m的值和一次函数的表达式;
(2)在X轴上求点P,使△CAP为等腰三角形(求出所有符合条件的点)
25、如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B
向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,
HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
答案部分
一、单选题
1、
【答案】C
2、
【答案】D
3、
【答案】B
4、
【答案】B
5、
【答案】A
6、
【答案】D
7、
【答案】A
8、
【答案】D
9、
【答案】D
10、
【答案】C
11、
【答案】C
12、
【答案】A
13、
【答案】C
14、
【答案】D
15、
【答案】C
二、填空题
16、
【答案】25
17、
【答案】3
18、
【答案】20
19、
【答案】边边边公理(SSS);AD⊥BC
20、
【答案】10
三、解答题
21、
【答案】14
22、
【答案】 解:△ABC是等腰三角形,
理由是:∵BC=18cm,BC边上的中线为AD,
∴BD=CD=9cm
∵AB=41cm,BC=18cm,AD=40cm
∴AB2=1681,
BD2+AD2=1681,
∴AB2=BD2+AD2
,
∴AD⊥BC
∵BD=CD,
∴AC=AB
∴△ABC是等腰三角形.
23、
【答案】证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
24、
【答案】解:(1)∵点C(m,6)在反比例函数上
∴6m=-24,∴m=-4,
∴点C的坐标是(-4,6),
∵轴,∴D的坐标是(-4,0),
又∵OA=OD,∴A的坐标为(4,0),
将A(4,0),C(-4,6)代入
得
解得
∴一次函数的表达式为
⑵如图:
①若以PA为底,则PD=AD=8,
∴OP=12,∴P(-12,0);
②若以PC为底,则AP=AC==10,
当P在A左侧时,OP=6,∴P(-6,0);
当P在A右侧时,OP=14,∴P(14,0);
③若以AC为底,设AP=PC=x,则DP=8-x,
∴x2=(8-x)2+62
,
解得x=.
∴OP=-4=,∴P(,0)
25、
【答案】解:(1)∵A、D关于点Q成中心对称,HQ⊥AB,
∴HQD=C=90°,HD=HA,
∴HDQ=A,
∴△DHQ∽△ABC.
(2)(
3
)略
同步练习
一、单选题
1、下列说法错误的是(
)
A、等腰三角形两腰上的中线相等
B、等腰三角形两腰上的高线相等
C、等腰三角形的中线与高重合
D、等腰三角形底边的中线上任一点到两腰的距离相等
2、如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、
F,则下列四个结论中,①AB上有一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相
等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是( )
A、1个
B、2
个
C、3
个
D、4个
3、如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C为 ( ).
A、25°
B、35°
C、40°
D、50°
4、如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
A、20°
B、30°
C、35°
D、40°
5、△ABC中,
∠B=30°,
∠C=50°,
点B、点C分别在线段AD、AE的中垂线上,
则∠EAD=
( )
A、40°
B、50°
C、80°
D、60°
6、已知a,b,c为△ABC三边,且满足a2c2-b2c2=a4-b4
,
则它的形状为 ( )
A、等边三角形
B、直角三角形
C、等腰三角形
D、等腰三角形或直角三角形
7、如图,在梯形ABCD中,AD//BC,
∠B=70°∠C=40°,DE//AB交BC于点E.若AD=3,BC=10,则CD的长是(
)
A、7
B、10
C、13
D、14
8、如图,直角坐标系中,点A(-2,2)、B(0,1)点P在x轴上,且是等腰三角形,则满足条件的点P共有( )个
A、1
B、2
C、3
D、4
9、如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF=AD,那么平行四边形ABCD应满足的条件是()
A、∠ABC=60°
B、AB:BC=1:4
C、AB:BC=5:2
D、AB:BC=5:8
10、如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( )
A、
B、4
C、
D、
11、若等腰三角形的两边长分别为4和8,则它的周长为( )
A、12
B、16
C、20
D、16或20
12、已知等腰三角形两边a,b,满足|2a﹣3b+5|+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
A、7或8
B、6或10
C、6或7
D、7或10
13、一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为多少平方厘米( )
A、50
B、50或40
C、50或40或30
D、50或30或20
14、在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
A、②③
B、③④
C、①②④
D、②③④
15、如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1
,
P2
,
…P10
,
记Mi=APi2+PiB PiC(i=1,2,…,10),那么M1+M2+…+M10的值为( )
A、4
B、14
C、40
D、不能确定
二、填空题
16、如图,∠A
=∠D
,
OA=OD,
∠DOC=50°,则∠DBC=________度.
17、如图∠AOP=∠BOP=15°,PC∥OA
,
PD⊥OA
,
若PC=6,则PD等于________.
18、若等腰三角形的两边分别是一元二次方程x2﹣12x+32=0的两根,则等腰三角形的周长为________ .
19、如图4所示,在△ABC中,AB=AC
,
D为BC的中点,则△ABD≌△ACD
,
根据是________ ,AD与BC的位置关系是________ .
20、△ABC中,∠A=90°,AB=AC
,
BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第________张.
三、解答题
21、已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,求三角形ABC的周长
22、一如图,在△ABC中,AB=41cm,BC=18cm,BC边上的中线AD=40cm.△ABC是等腰三角形吗?为什么?
23、如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
24、如图一次函数的图象分别交x轴、y轴于点A,B,与反比例函数图象在第二象限交于点C(m,6),轴于点D,OA=OD.
(1)求m的值和一次函数的表达式;
(2)在X轴上求点P,使△CAP为等腰三角形(求出所有符合条件的点)
25、如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B
向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,
HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
答案部分
一、单选题
1、
【答案】C
2、
【答案】D
3、
【答案】B
4、
【答案】B
5、
【答案】A
6、
【答案】D
7、
【答案】A
8、
【答案】D
9、
【答案】D
10、
【答案】C
11、
【答案】C
12、
【答案】A
13、
【答案】C
14、
【答案】D
15、
【答案】C
二、填空题
16、
【答案】25
17、
【答案】3
18、
【答案】20
19、
【答案】边边边公理(SSS);AD⊥BC
20、
【答案】10
三、解答题
21、
【答案】14
22、
【答案】 解:△ABC是等腰三角形,
理由是:∵BC=18cm,BC边上的中线为AD,
∴BD=CD=9cm
∵AB=41cm,BC=18cm,AD=40cm
∴AB2=1681,
BD2+AD2=1681,
∴AB2=BD2+AD2
,
∴AD⊥BC
∵BD=CD,
∴AC=AB
∴△ABC是等腰三角形.
23、
【答案】证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
24、
【答案】解:(1)∵点C(m,6)在反比例函数上
∴6m=-24,∴m=-4,
∴点C的坐标是(-4,6),
∵轴,∴D的坐标是(-4,0),
又∵OA=OD,∴A的坐标为(4,0),
将A(4,0),C(-4,6)代入
得
解得
∴一次函数的表达式为
⑵如图:
①若以PA为底,则PD=AD=8,
∴OP=12,∴P(-12,0);
②若以PC为底,则AP=AC==10,
当P在A左侧时,OP=6,∴P(-6,0);
当P在A右侧时,OP=14,∴P(14,0);
③若以AC为底,设AP=PC=x,则DP=8-x,
∴x2=(8-x)2+62
,
解得x=.
∴OP=-4=,∴P(,0)
25、
【答案】解:(1)∵A、D关于点Q成中心对称,HQ⊥AB,
∴HQD=C=90°,HD=HA,
∴HDQ=A,
∴△DHQ∽△ABC.
(2)(
3
)略
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
