1.4 解直角三角形 同步练习(含答案)
文档属性
| 名称 | 1.4 解直角三角形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 275.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 18:45:19 | ||
图片预览



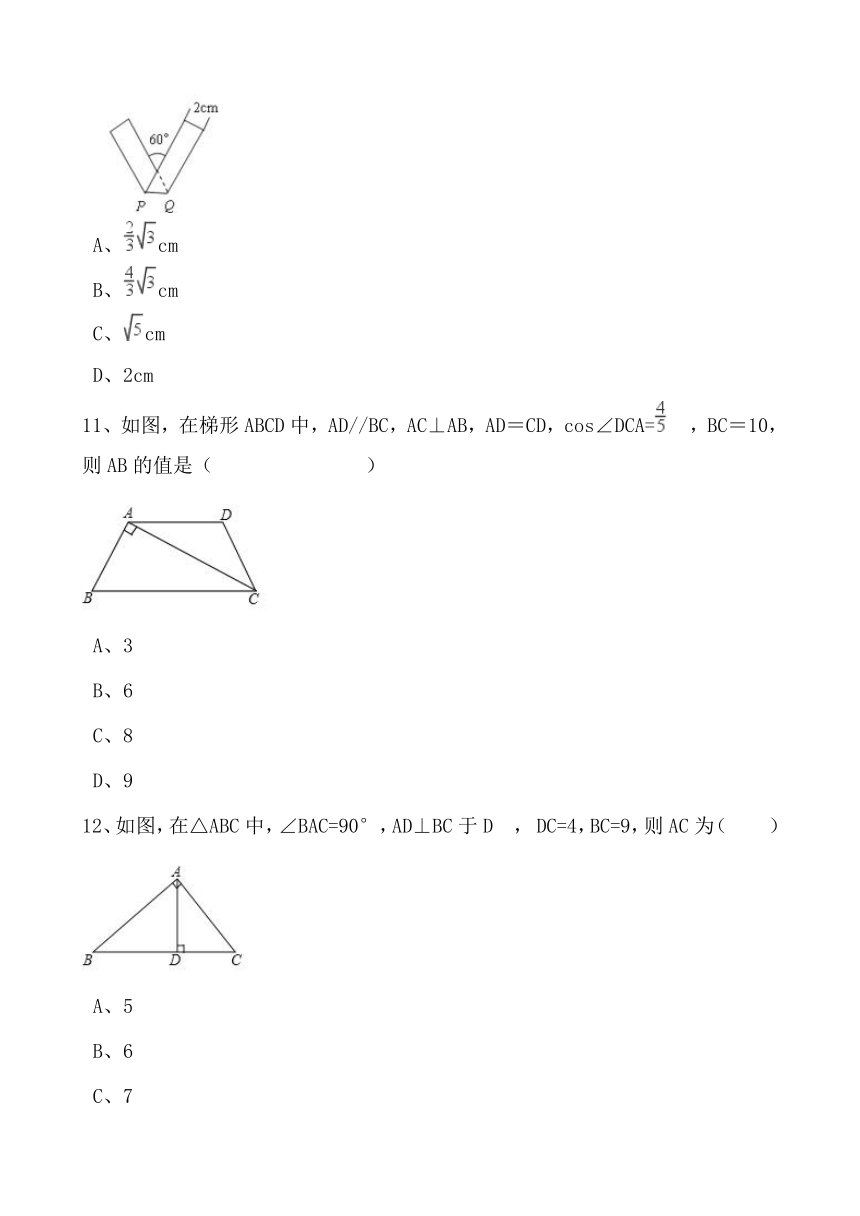
文档简介
1.4
解直角三角形
同步练习
一、单选题
1、菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sinA=,则下列结论正确的个数有( )
①DE=3cm;
②BE=1cm;
③菱形的面积为15cm2;
④BD=2cm.
A、1个
B、2个
C、3个
D、4个
2、如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=,
则下列结论中正确的个数为(
)
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
A、3个
B、2个
C、1个
D、0个
3、如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与X轴正半轴的夹角为a,且cosα=,
则点P的坐标是( ).
A、(2,3)
B、(2,)
C、(,
2)
D、(2,)
4、如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为(
)
A、2
B、4
C、8
D、8
5、如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
A、10米
B、15米
C、25米
D、30米
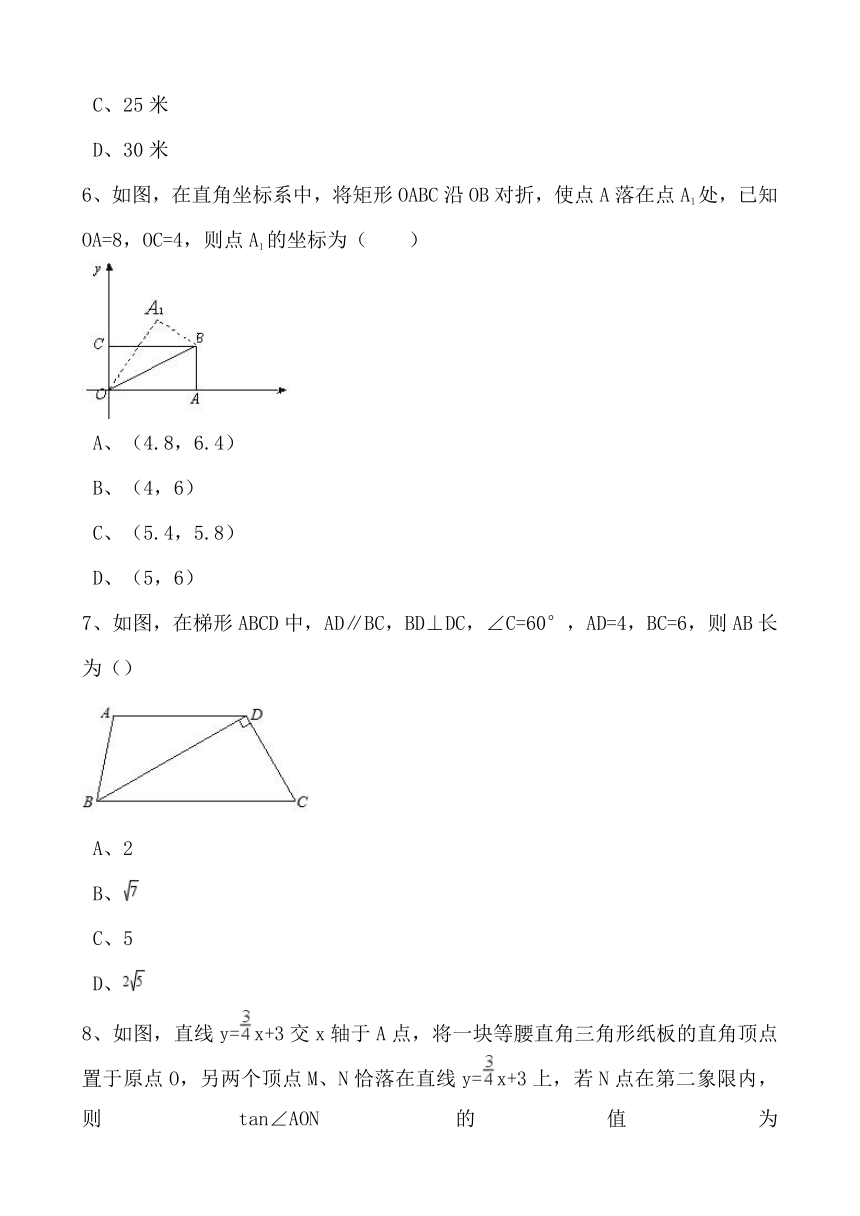
6、如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
A、(4.8,6.4)
B、(4,6)
C、(5.4,5.8)
D、(5,6)
7、如图,在梯形ABCD中,AD∥BC,BD⊥DC,∠C=60°,AD=4,BC=6,则AB长为()
A、2
B、
C、5
D、
8、如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为( )
A、
B、
C、
D、
9、小阳发现电线杆AB的影子落在土坡的破面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30
角,且此时测得1米杆的影长为2米,则
电线杆的高度为(
)
A、9米
B、28米
C、(7+)米
D、(14+)米
10、将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是(
)
A、cm
B、cm
C、cm
D、2cm
11、如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA= ,BC=10,则AB的值是(
)
A、3
B、6
C、8
D、9
12、如图,在△ABC中,∠BAC=90°,AD⊥BC于D
,
DC=4,BC=9,则AC为( )
A、5
B、6
C、7
D、8
13、在△ABC中,∠A,∠B均为锐角,且sinA=,
cosB=,
AC=40,则△ABC的面积是( )
A、800
B、800
C、400
D、400
14、如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=,
则AB的长为( )
A、
B、
C、
D、12
15、一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为(
)
A、75cm2
B、(25+25)cm2
C、(25+)cm2
D、(25+)cm2
二、填空题
16、在Rt△ABC中,∠A=90°,AB=2,若sinC=,
则BC的长度为________
17、如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,
则cos∠ADC=________.
18、如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,
则AD的长为________.
19、(2016 菏泽)如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.
20、如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE=________
三、解答题
21、如图,矩形ABCD的对角线AC.BD相交于点O
,
过点O作OE⊥AC交AD于E
,
若AB=6,AD=8,求sin∠OEA的值
.
22、如图,AD是△ABC的中线,tanB=,
cosC=,
AC=.
求:
(1)BC的长;
(2)sin∠ADC的值.
23、如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
24、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于E,AE=1.求梯形ABCD的高.
25、已知,如图,△ABC中.AD⊥BC于D,AC=10,BC=21,△ABC面积为84,求sinBcosC+cosBsinC的值.
答案部分
一、单选题
1、
【答案】C
2、
【答案】A
3、
【答案】D
4、
【答案】B
5、
【答案】B
6、
【答案】A
7、
【答案】B
8、
【答案】A
9、
【答案】D
10、
【答案】B
11、
【答案】B
12、
【答案】B
13、
【答案】D
14、
【答案】D
15、
【答案】C
二、填空题
16、
【答案】10
17、
【答案】
18、
【答案】2
19、
【答案】
20、
【答案】
三、解答题
21、
【答案】解:连接EC
,
∵四边形ABCD为矩形,
∴OA=OC
,
∠ABC=90°,
利用勾股定理得:AC=
=10,即OA=5,
∵OE⊥AC
,
∴AE=CE
,
在Rt△EDC中,设EC=AE=x
,
则有ED=AD-AE=8-x
,
DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x=
,
∴AE=
,
在Rt△AOE中,sin∠OEA=
.
22、
【答案】解:(1)过点A作AE⊥BC于点E,
∵cosC=,
∴∠C=45°,
在Rt△ACE中,CE=AC cosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=,即=,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=.
23、
【答案】解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
24、
【答案】解:∵AD∥BC,
∴∠2=∠3
又AB=AD,
∴∠1=∠3
∠ABC=∠C=60°
∴∠1=∠2=30°
在Rt△ABE中,AE=1,∠1=30°,
∴AB=2
作AF⊥BC垂足为F,
在Rt△ABF中,AF=AB sin∠ABC=AB sin60°=2×=
∴梯形ABCD的高为.
25、
【答案】解:如图,∵AD⊥BC,S△ABC=84,BC=21,
∴BC AD=84,即×21×AD=84,解得,AD=8
∵AC=10,
∴在直角△ACD中,由勾股定理得到:CD==6
∴在直角△ABD中,BD=15,AB==17
∴sinB==,cosB==,sinC==,cosC==
∴sinBcosC+cosBsinC=×+×=.
解直角三角形
同步练习
一、单选题
1、菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sinA=,则下列结论正确的个数有( )
①DE=3cm;
②BE=1cm;
③菱形的面积为15cm2;
④BD=2cm.
A、1个
B、2个
C、3个
D、4个
2、如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=,
则下列结论中正确的个数为(
)
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
A、3个
B、2个
C、1个
D、0个
3、如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与X轴正半轴的夹角为a,且cosα=,
则点P的坐标是( ).
A、(2,3)
B、(2,)
C、(,
2)
D、(2,)
4、如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为(
)
A、2
B、4
C、8
D、8
5、如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
A、10米
B、15米
C、25米
D、30米
6、如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
A、(4.8,6.4)
B、(4,6)
C、(5.4,5.8)
D、(5,6)
7、如图,在梯形ABCD中,AD∥BC,BD⊥DC,∠C=60°,AD=4,BC=6,则AB长为()
A、2
B、
C、5
D、
8、如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为( )
A、
B、
C、
D、
9、小阳发现电线杆AB的影子落在土坡的破面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30
角,且此时测得1米杆的影长为2米,则
电线杆的高度为(
)
A、9米
B、28米
C、(7+)米
D、(14+)米
10、将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是(
)
A、cm
B、cm
C、cm
D、2cm
11、如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA= ,BC=10,则AB的值是(
)
A、3
B、6
C、8
D、9
12、如图,在△ABC中,∠BAC=90°,AD⊥BC于D
,
DC=4,BC=9,则AC为( )
A、5
B、6
C、7
D、8
13、在△ABC中,∠A,∠B均为锐角,且sinA=,
cosB=,
AC=40,则△ABC的面积是( )
A、800
B、800
C、400
D、400
14、如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=,
则AB的长为( )
A、
B、
C、
D、12
15、一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为(
)
A、75cm2
B、(25+25)cm2
C、(25+)cm2
D、(25+)cm2
二、填空题
16、在Rt△ABC中,∠A=90°,AB=2,若sinC=,
则BC的长度为________
17、如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,
则cos∠ADC=________.
18、如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,
则AD的长为________.
19、(2016 菏泽)如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.
20、如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE=________
三、解答题
21、如图,矩形ABCD的对角线AC.BD相交于点O
,
过点O作OE⊥AC交AD于E
,
若AB=6,AD=8,求sin∠OEA的值
.
22、如图,AD是△ABC的中线,tanB=,
cosC=,
AC=.
求:
(1)BC的长;
(2)sin∠ADC的值.
23、如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
24、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于E,AE=1.求梯形ABCD的高.
25、已知,如图,△ABC中.AD⊥BC于D,AC=10,BC=21,△ABC面积为84,求sinBcosC+cosBsinC的值.
答案部分
一、单选题
1、
【答案】C
2、
【答案】A
3、
【答案】D
4、
【答案】B
5、
【答案】B
6、
【答案】A
7、
【答案】B
8、
【答案】A
9、
【答案】D
10、
【答案】B
11、
【答案】B
12、
【答案】B
13、
【答案】D
14、
【答案】D
15、
【答案】C
二、填空题
16、
【答案】10
17、
【答案】
18、
【答案】2
19、
【答案】
20、
【答案】
三、解答题
21、
【答案】解:连接EC
,
∵四边形ABCD为矩形,
∴OA=OC
,
∠ABC=90°,
利用勾股定理得:AC=
=10,即OA=5,
∵OE⊥AC
,
∴AE=CE
,
在Rt△EDC中,设EC=AE=x
,
则有ED=AD-AE=8-x
,
DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x=
,
∴AE=
,
在Rt△AOE中,sin∠OEA=
.
22、
【答案】解:(1)过点A作AE⊥BC于点E,
∵cosC=,
∴∠C=45°,
在Rt△ACE中,CE=AC cosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=,即=,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=.
23、
【答案】解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
24、
【答案】解:∵AD∥BC,
∴∠2=∠3
又AB=AD,
∴∠1=∠3
∠ABC=∠C=60°
∴∠1=∠2=30°
在Rt△ABE中,AE=1,∠1=30°,
∴AB=2
作AF⊥BC垂足为F,
在Rt△ABF中,AF=AB sin∠ABC=AB sin60°=2×=
∴梯形ABCD的高为.
25、
【答案】解:如图,∵AD⊥BC,S△ABC=84,BC=21,
∴BC AD=84,即×21×AD=84,解得,AD=8
∵AC=10,
∴在直角△ACD中,由勾股定理得到:CD==6
∴在直角△ABD中,BD=15,AB==17
∴sinB==,cosB==,sinC==,cosC==
∴sinBcosC+cosBsinC=×+×=.
