2.2 二次函数的图像与性质 同步练习(含答案)
文档属性
| 名称 | 2.2 二次函数的图像与性质 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 18:56:23 | ||
图片预览




文档简介
2.2
二次函数的图像与性质
同步练习
一、单选题
1、①y=-x;②y=2x;③y=-;④y=x2(x<0),y随x的增大而减小的函数有( )
A、1个
B、2个
C、3个
D、4个
2、对于抛物线y=(x-5)2+3,下列说法正确的是( )
A、开口向下,顶点坐标(5,3)
B、开口向上,顶点坐标(5,3)
C、开口向下,顶点坐标(-5,3)
D、开口向上,顶点坐标(-5,3)
3、下列函数中,当x>0时,y随x的增大而增大的是(
)
A、y=-x+1
B、y=x2-1
C、
D、y=-x2+1
4、如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0
;②2a+b=0;③a+b+c>0
;④当-1<x<3时,y>0.其中正确的个数为(
)
A、1
B、2
C、3
D、4
5、二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是( )
A、0<t<2
B、0<t<1
C、1<t<2
D、﹣1<t<1
6、如图所示的抛物线是二次函数y=ax2-3x+a2-1的图像,那么下列结论错误的是
( )
A、当y<0时,x>0
B、当-3<x<0时,y>0
C、当x<时,y随x的增大而增大
D、抛物线可由抛物线y=-x2平移得到
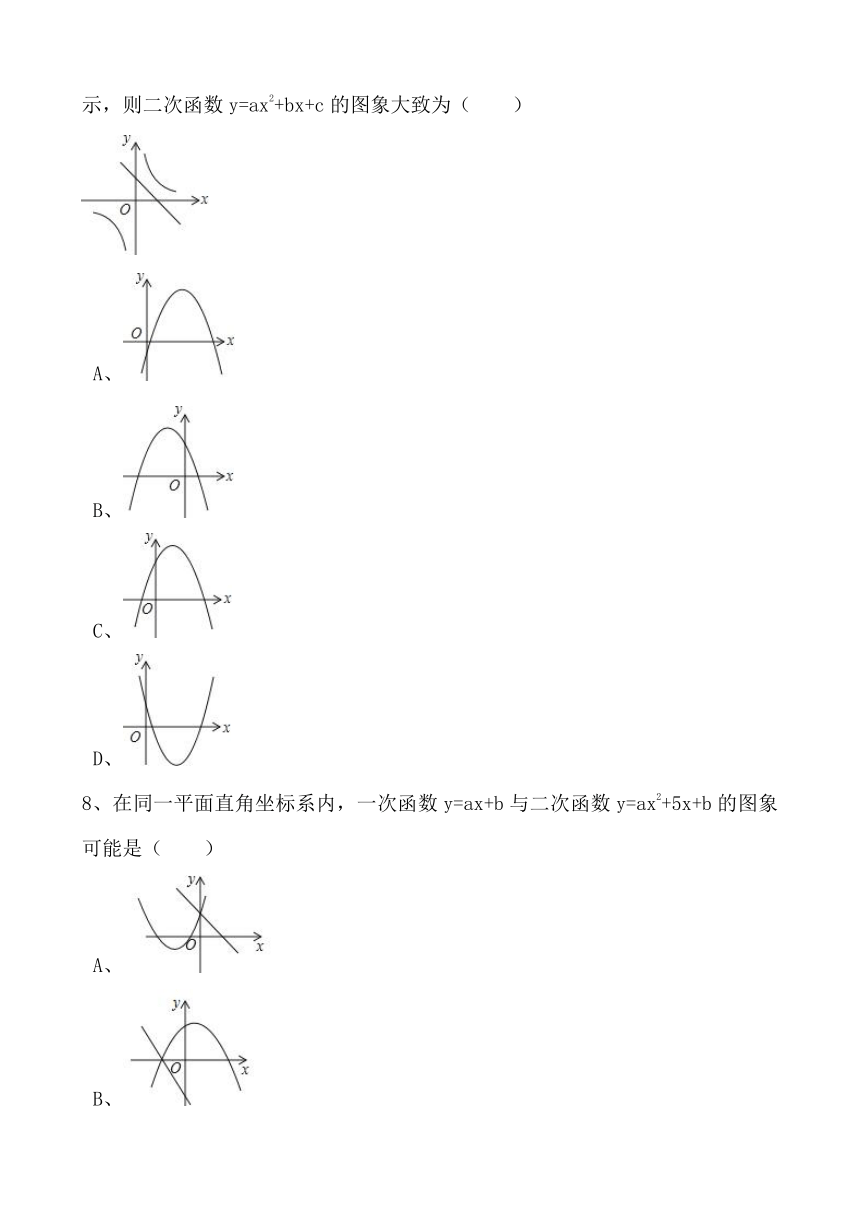
7、一次函数y=ax+b和反比例函数y=
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
A、
B、
C、
D、
8、在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )
A、
B、
C、
D、
9、定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为
[m,1-m,-1]的函数的一些结论:
①
当m=-1时,函数图象的顶点坐标是(1,0);
②
当m>0时,函数图象截x轴所得的线段长度大于1;
③
当m<0时,函数在x>时,y随x的增大而减小;
④
不论m取何值,函数图象经过一个定点.
其中正确的结论有 ( )
A、4个
B、3个
C、2个
D、1个
10、已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果
①>4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是(
)
A、①②③④
B、②④⑤
C、②③④
D、①④⑤
11、y=(x-1)2+2的对称轴是直线(
)
A、x=-1
B、x=1
C、y=-1
D、y=1
12、下列函数中,满足y的值随x的值增大而增大的是( )
A、y=﹣2x
B、y=3x﹣1
C、y=
D、y=x2
13、已知二次函数y=a(x-2)2+c(a>0),当自变量x分别取
、3、0时,对应的函数值分别:y1
,
y2
,
y3
,
则y1
,
y2
,
y3的大小关系正确的是( )
A、y3B、y1C、y2D、y314、在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A、y=﹣(x﹣
)2﹣
B、y=﹣(x+
)2﹣
C、y=﹣(x﹣
)2﹣
D、y=﹣(x+
)2+
15、已知二次函数y=ax2+bx+1,一次函数y=k(x-1)-,
若它们的图象对于任意的非零实数k都只有一个公共点,则a,b的值分别为( )
A、a=1,b=2
B、a=1,b=-2
C、a=-1,b=2
D、a=-1,b=-2
二、填空题
16、若将函数y=2x2的图象向左平移1个单位,再向上平移2个单位,可得到的抛物线是________.
17、已知二次函数的对称轴为x=2,则b=________ .
18、已知二次函数
的图象开口向下,则m的值为________.
19、点A(x1,y1)、B(x2,y2)在二次函数的图象上,若x2>x1≥m,有y2>y1,则m的取值范围为________.
20、已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,则m的取值范围是________.
三、解答题
21、已知二次函数的图象与x轴有且只有一个公共点.
(1)求该二次函数的图象的顶点坐标;
(2)若P(n,y1),Q(n+2,y2)是该二次函数的图象上的两点,且y1>y2
,
求实数n的取值范围.
22、已知抛物线y=x2﹣2x+1.
(1)求它的对称轴和顶点坐标;
(2)根据图象,确定当x>2时,y的取值范围.
23、如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是多少?
24、如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b(x-2)2+m的x的取值范围.
25、已知抛物线C1:y1=2x2﹣4x+k与x轴只有一个公共点.
(1)求k的值;
(2)怎样平移抛物线C1就可以得到抛物线C2:y2=2(x+1)2﹣4k?请写出具体的平移方法;
(3)若点A(1,t)和点B(m,n)都在抛物线C2:y2=2(x+1)2﹣4k上,且n<t,直接写出m的取值范围.
答案部分
一、单选题
1、
【答案】B
2、
【答案】A
3、
【答案】B
4、
【答案】C
5、
【答案】A
6、
【答案】A
7、
【答案】C
8、
【答案】C
9、
【答案】B
10、
【答案】D
11、
【答案】B
12、
【答案】B
13、
【答案】B
14、
【答案】A
15、
【答案】B
二、填空题
16、
【答案】y=2(x+1)2+2
17、
【答案】-4
18、
【答案】
19、
【答案】m≥2
20、
【答案】m≥﹣1
三、解答题
21、
【答案】解:(1)
=,对称轴x=-1
∵与x轴有且只有一个公共点,∴顶点的纵坐标为0.
∴函数图象的顶点坐标为(—1,0)
或:与x轴有且只有一个公共点,∴22
-4m=0,
∴m=1,
∴函数=(x+1)2
∴函数图象的顶点坐标是(-1,0)
(2)∵P(n,y1),Q(n+2,y2)是该二次函数的图象上的两点,且y1>y2
,
n2+2n+1>(n+2)2+2(n+2)+1
,
化简整理得,4n+8<0,
∴n
<
-2,
∴实数n的取值范围是n
<
-2.
22、
【答案】解:(1)y=x2﹣2x+1=(x﹣1)2
,
对称轴为直线x=1,顶点坐标为(1,0);
(2)抛物线图象如下图所示:
由图象可知当x>2时,y的取值范围是y>1.
23、
【答案】解:由图象知,图中两个二次函数关于x轴对称,故把x轴下半部分阴影部分面积移到x轴上半部分,则所有的阴影部分面积是半个正方形的面积,故为2.
24、
【答案】解;(1)将点A(1,0)代入y=(x-2)2+m得(1-2)2+m=0,解得m=-1,
所以二次函数解析式为y=(x-2)2-1;
当x=0时,y=4-1=3,
所以C点坐标为(0,3),
由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2,
所以B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得
,解得,
所以一次函数解析式为y=x-1;
(2)观察图像可得x的取值范围:x≤1或x≥4.
25、
【答案】解:(1)根据题意得:△=16﹣8k=0,解得:k=2;
(2)C1是:y1=2x2﹣4x+2=2(x﹣1)2
,
抛物线C2是:y2=2(x+1)2﹣8.
则平移抛物线C1就可以得到抛物线C2的方法是向右平移2个单位长度,向下平移8个单位长度;
(3)当x=1时,y2=2(x+1)2﹣8=0,即t=0.
在y2=2(x+1)2﹣8中,令y=0,解得:x=1或﹣3.
则当n<t时,即2(x+1)2﹣8<0时,m的范围是﹣3<m<1.
二次函数的图像与性质
同步练习
一、单选题
1、①y=-x;②y=2x;③y=-;④y=x2(x<0),y随x的增大而减小的函数有( )
A、1个
B、2个
C、3个
D、4个
2、对于抛物线y=(x-5)2+3,下列说法正确的是( )
A、开口向下,顶点坐标(5,3)
B、开口向上,顶点坐标(5,3)
C、开口向下,顶点坐标(-5,3)
D、开口向上,顶点坐标(-5,3)
3、下列函数中,当x>0时,y随x的增大而增大的是(
)
A、y=-x+1
B、y=x2-1
C、
D、y=-x2+1
4、如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0
;②2a+b=0;③a+b+c>0
;④当-1<x<3时,y>0.其中正确的个数为(
)
A、1
B、2
C、3
D、4
5、二次函数y=ax2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t值的变化范围是( )
A、0<t<2
B、0<t<1
C、1<t<2
D、﹣1<t<1
6、如图所示的抛物线是二次函数y=ax2-3x+a2-1的图像,那么下列结论错误的是
( )
A、当y<0时,x>0
B、当-3<x<0时,y>0
C、当x<时,y随x的增大而增大
D、抛物线可由抛物线y=-x2平移得到
7、一次函数y=ax+b和反比例函数y=
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
A、
B、
C、
D、
8、在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )
A、
B、
C、
D、
9、定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为
[m,1-m,-1]的函数的一些结论:
①
当m=-1时,函数图象的顶点坐标是(1,0);
②
当m>0时,函数图象截x轴所得的线段长度大于1;
③
当m<0时,函数在x>时,y随x的增大而减小;
④
不论m取何值,函数图象经过一个定点.
其中正确的结论有 ( )
A、4个
B、3个
C、2个
D、1个
10、已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果
①>4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是(
)
A、①②③④
B、②④⑤
C、②③④
D、①④⑤
11、y=(x-1)2+2的对称轴是直线(
)
A、x=-1
B、x=1
C、y=-1
D、y=1
12、下列函数中,满足y的值随x的值增大而增大的是( )
A、y=﹣2x
B、y=3x﹣1
C、y=
D、y=x2
13、已知二次函数y=a(x-2)2+c(a>0),当自变量x分别取
、3、0时,对应的函数值分别:y1
,
y2
,
y3
,
则y1
,
y2
,
y3的大小关系正确的是( )
A、y3
A、y=﹣(x﹣
)2﹣
B、y=﹣(x+
)2﹣
C、y=﹣(x﹣
)2﹣
D、y=﹣(x+
)2+
15、已知二次函数y=ax2+bx+1,一次函数y=k(x-1)-,
若它们的图象对于任意的非零实数k都只有一个公共点,则a,b的值分别为( )
A、a=1,b=2
B、a=1,b=-2
C、a=-1,b=2
D、a=-1,b=-2
二、填空题
16、若将函数y=2x2的图象向左平移1个单位,再向上平移2个单位,可得到的抛物线是________.
17、已知二次函数的对称轴为x=2,则b=________ .
18、已知二次函数
的图象开口向下,则m的值为________.
19、点A(x1,y1)、B(x2,y2)在二次函数的图象上,若x2>x1≥m,有y2>y1,则m的取值范围为________.
20、已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,则m的取值范围是________.
三、解答题
21、已知二次函数的图象与x轴有且只有一个公共点.
(1)求该二次函数的图象的顶点坐标;
(2)若P(n,y1),Q(n+2,y2)是该二次函数的图象上的两点,且y1>y2
,
求实数n的取值范围.
22、已知抛物线y=x2﹣2x+1.
(1)求它的对称轴和顶点坐标;
(2)根据图象,确定当x>2时,y的取值范围.
23、如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是多少?
24、如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b(x-2)2+m的x的取值范围.
25、已知抛物线C1:y1=2x2﹣4x+k与x轴只有一个公共点.
(1)求k的值;
(2)怎样平移抛物线C1就可以得到抛物线C2:y2=2(x+1)2﹣4k?请写出具体的平移方法;
(3)若点A(1,t)和点B(m,n)都在抛物线C2:y2=2(x+1)2﹣4k上,且n<t,直接写出m的取值范围.
答案部分
一、单选题
1、
【答案】B
2、
【答案】A
3、
【答案】B
4、
【答案】C
5、
【答案】A
6、
【答案】A
7、
【答案】C
8、
【答案】C
9、
【答案】B
10、
【答案】D
11、
【答案】B
12、
【答案】B
13、
【答案】B
14、
【答案】A
15、
【答案】B
二、填空题
16、
【答案】y=2(x+1)2+2
17、
【答案】-4
18、
【答案】
19、
【答案】m≥2
20、
【答案】m≥﹣1
三、解答题
21、
【答案】解:(1)
=,对称轴x=-1
∵与x轴有且只有一个公共点,∴顶点的纵坐标为0.
∴函数图象的顶点坐标为(—1,0)
或:与x轴有且只有一个公共点,∴22
-4m=0,
∴m=1,
∴函数=(x+1)2
∴函数图象的顶点坐标是(-1,0)
(2)∵P(n,y1),Q(n+2,y2)是该二次函数的图象上的两点,且y1>y2
,
n2+2n+1>(n+2)2+2(n+2)+1
,
化简整理得,4n+8<0,
∴n
<
-2,
∴实数n的取值范围是n
<
-2.
22、
【答案】解:(1)y=x2﹣2x+1=(x﹣1)2
,
对称轴为直线x=1,顶点坐标为(1,0);
(2)抛物线图象如下图所示:
由图象可知当x>2时,y的取值范围是y>1.
23、
【答案】解:由图象知,图中两个二次函数关于x轴对称,故把x轴下半部分阴影部分面积移到x轴上半部分,则所有的阴影部分面积是半个正方形的面积,故为2.
24、
【答案】解;(1)将点A(1,0)代入y=(x-2)2+m得(1-2)2+m=0,解得m=-1,
所以二次函数解析式为y=(x-2)2-1;
当x=0时,y=4-1=3,
所以C点坐标为(0,3),
由于C和B关于对称轴对称,而抛物线的对称轴为直线x=2,
所以B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得
,解得,
所以一次函数解析式为y=x-1;
(2)观察图像可得x的取值范围:x≤1或x≥4.
25、
【答案】解:(1)根据题意得:△=16﹣8k=0,解得:k=2;
(2)C1是:y1=2x2﹣4x+2=2(x﹣1)2
,
抛物线C2是:y2=2(x+1)2﹣8.
则平移抛物线C1就可以得到抛物线C2的方法是向右平移2个单位长度,向下平移8个单位长度;
(3)当x=1时,y2=2(x+1)2﹣8=0,即t=0.
在y2=2(x+1)2﹣8中,令y=0,解得:x=1或﹣3.
则当n<t时,即2(x+1)2﹣8<0时,m的范围是﹣3<m<1.
