1.2 30°、45°、60°角的三角函数值 同步练习(含答案)
文档属性
| 名称 | 1.2 30°、45°、60°角的三角函数值 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 171.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 19:19:38 | ||
图片预览




文档简介
1.2
30°、45°、60°角的三角函数值
同步练习
一、单选题
1、计算sin45°的结果等于(
)
A、
B、1
C、
D、
2、已知tan,则锐角α的度数是( )
A、60°
B、45°
C、50°
D、75°
3、在实数π、、、sin30°,无理数的个数为(
)
A、1
B、2
C、3
D、4
4、在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则此三角形是(
)
A、锐角三角形
B、直角三角形
C、钝角三角形
D、形状不能确定
5、如果∠a是等腰直角三角形的一个锐角,则tana的值是( )
A、
B、
C、1
D、
6、点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )
A、(,)
B、(-,-)
C、(-,)
D、(-,-)
7、△ABC中,∠A,∠B均为锐角,且有,则△ABC是( )
A、直角(不等腰)三角形
B、等腰直角三角形
C、等腰(不等边)三角形
D、等边三角形
8、已知α为锐角,且tan(90°-α)=,则α的度数为( )
A、30°
B、60°
C、45°
D、75°
9、在△ABC中,∠C
=90o
,
若cosB=
,则∠B的值为( ).
A、
B、
C、
D、
10、在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是( )
A、45°
B、60°
C、75°
D、105°
11、在Rt△ABC中,∠C=90°,∠B=60°,那么sinA+cosB的值为( )
A、1
B、
C、
D、
12、若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为( )
A、
B、
C、
D、
13、关于x的一元二次方程x2﹣
x+sinα=0有两个相等的实数根,则锐角α等于( )
A、15°
B、30°
C、45°
D、60°
14、如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积是
A、
B、
C、
D、3
15、如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一动点,则PA+PC的最小值为
A、
B、
C、
D、2
二、填空题
16、计算=________
.
17、在Rt△ABC中,∠C=90°,如果3a=b,那么sinA=________
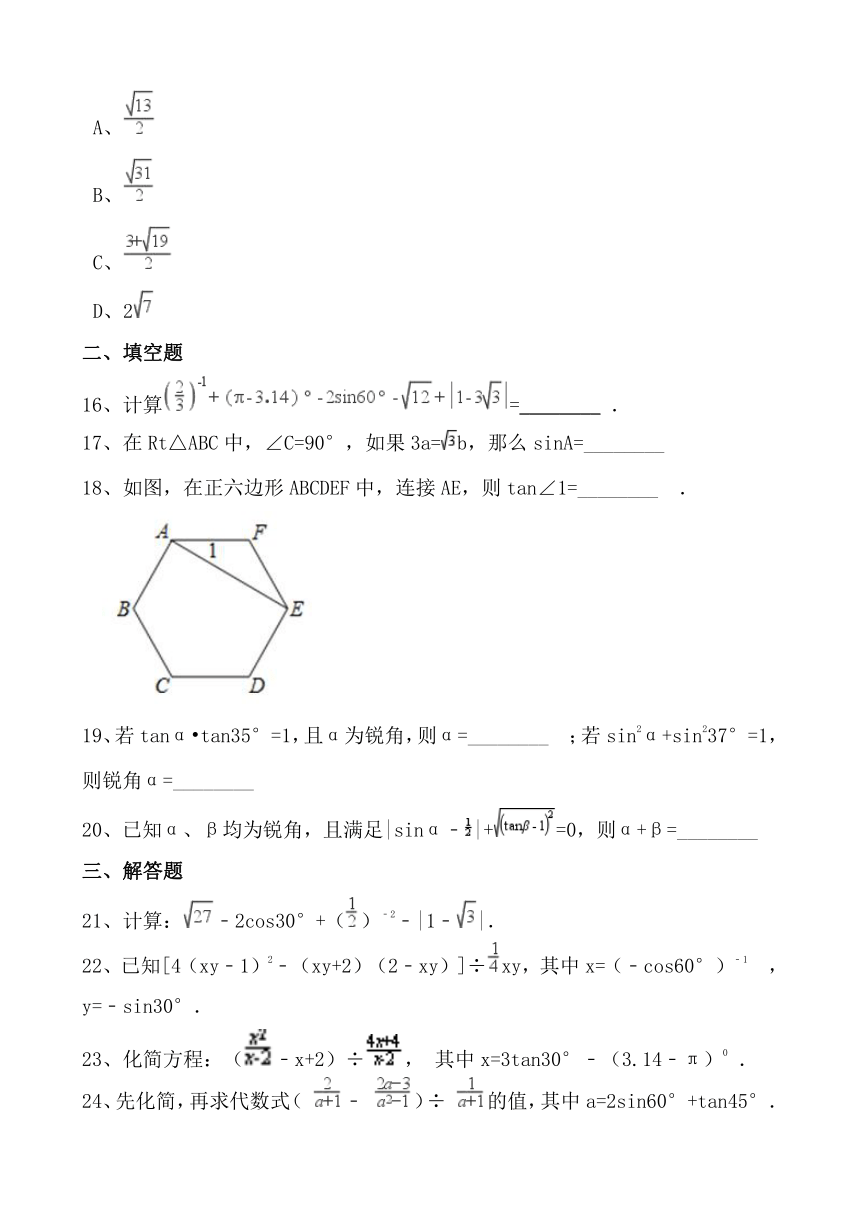
18、如图,在正六边形ABCDEF中,连接AE,则tan∠1=________ .
19、若tanα tan35°=1,且α为锐角,则α=________ ;若sin2α+sin237°=1,则锐角α=________
20、已知α、β均为锐角,且满足|sinα﹣|+=0,则α+β=________
三、解答题
21、计算:﹣2cos30°+()﹣2﹣|1﹣|.
22、已知[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy,其中x=(﹣cos60°)﹣1
,
y=﹣sin30°.
23、化简方程:(﹣x+2)÷,
其中x=3tan30°﹣(3.14﹣π)0
.
24、先化简,再求代数式(
﹣
)÷
的值,其中a=2sin60°+tan45°.
25、如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.
(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AB=2AD=4,求BD的长.
答案部分
一、单选题
1、
【答案】B
2、
【答案】C
3、
【答案】B
4、
【答案】C
5、
【答案】C
6、
【答案】B
7、
【答案】B
8、
【答案】A
9、
【答案】A
10、
【答案】D
11、
【答案】A
12、
【答案】C
13、
【答案】B
14、
【答案】C
15、
【答案】B
二、填空题
16、
【答案】
17、
【答案】
18、
【答案】
19、
【答案】55° ;53°
20、
【答案】75°
三、解答题
21、
【答案】解:原式=3﹣2×+4﹣(﹣1),
=3﹣+4﹣+1,
=+5.
22、
【答案】解:∵x=(﹣cos60°)﹣1=(﹣)﹣1=﹣2,y=﹣sin30°=﹣,
∴[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy
=[4(x2y2﹣2xy+1)﹣(22﹣x2y2)]
=(4x2y2﹣8xy+4﹣4+x2y2)
=(5x2y2﹣8xy)
=20xy﹣32
=20×(﹣2)×(﹣)﹣32
=﹣12.
23、
【答案】解:原式=÷
=×
=,
当x=3×﹣1=﹣1时,
原式==1﹣.
24、
【答案】解:原式=[
﹣
] (a+1)
=
(a+1)
=
(a+1)
=
(a+1)
=
,
当a=2sin60°+tan45°=2×
+1=
+1时,原式=
=
.
25、
【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB‖CD且AB=CD,
∵E,F分别是AB,CD的中点,
∴AE=AB
,
DF=DC
∴AE=DF,
∴四边形AEFD是平行四边形;
(2)解:过点D作DG⊥AB于点G.
∵AB=2AD=4,
∴AD=2.
在Rt△AGD中,∵∠AGD=90°,∠A=60°,AD=2,
∴AG=AD×cos60°=1
,DG=AD×sin60°=
∴BG=AB-AG=3
在Rt△DGB中,∵∠DGB=90°,DG=,BG=3,
∴BD===
30°、45°、60°角的三角函数值
同步练习
一、单选题
1、计算sin45°的结果等于(
)
A、
B、1
C、
D、
2、已知tan,则锐角α的度数是( )
A、60°
B、45°
C、50°
D、75°
3、在实数π、、、sin30°,无理数的个数为(
)
A、1
B、2
C、3
D、4
4、在△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则此三角形是(
)
A、锐角三角形
B、直角三角形
C、钝角三角形
D、形状不能确定
5、如果∠a是等腰直角三角形的一个锐角,则tana的值是( )
A、
B、
C、1
D、
6、点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )
A、(,)
B、(-,-)
C、(-,)
D、(-,-)
7、△ABC中,∠A,∠B均为锐角,且有,则△ABC是( )
A、直角(不等腰)三角形
B、等腰直角三角形
C、等腰(不等边)三角形
D、等边三角形
8、已知α为锐角,且tan(90°-α)=,则α的度数为( )
A、30°
B、60°
C、45°
D、75°
9、在△ABC中,∠C
=90o
,
若cosB=
,则∠B的值为( ).
A、
B、
C、
D、
10、在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是( )
A、45°
B、60°
C、75°
D、105°
11、在Rt△ABC中,∠C=90°,∠B=60°,那么sinA+cosB的值为( )
A、1
B、
C、
D、
12、若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为( )
A、
B、
C、
D、
13、关于x的一元二次方程x2﹣
x+sinα=0有两个相等的实数根,则锐角α等于( )
A、15°
B、30°
C、45°
D、60°
14、如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积是
A、
B、
C、
D、3
15、如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一动点,则PA+PC的最小值为
A、
B、
C、
D、2
二、填空题
16、计算=________
.
17、在Rt△ABC中,∠C=90°,如果3a=b,那么sinA=________
18、如图,在正六边形ABCDEF中,连接AE,则tan∠1=________ .
19、若tanα tan35°=1,且α为锐角,则α=________ ;若sin2α+sin237°=1,则锐角α=________
20、已知α、β均为锐角,且满足|sinα﹣|+=0,则α+β=________
三、解答题
21、计算:﹣2cos30°+()﹣2﹣|1﹣|.
22、已知[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy,其中x=(﹣cos60°)﹣1
,
y=﹣sin30°.
23、化简方程:(﹣x+2)÷,
其中x=3tan30°﹣(3.14﹣π)0
.
24、先化简,再求代数式(
﹣
)÷
的值,其中a=2sin60°+tan45°.
25、如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.
(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AB=2AD=4,求BD的长.
答案部分
一、单选题
1、
【答案】B
2、
【答案】C
3、
【答案】B
4、
【答案】C
5、
【答案】C
6、
【答案】B
7、
【答案】B
8、
【答案】A
9、
【答案】A
10、
【答案】D
11、
【答案】A
12、
【答案】C
13、
【答案】B
14、
【答案】C
15、
【答案】B
二、填空题
16、
【答案】
17、
【答案】
18、
【答案】
19、
【答案】55° ;53°
20、
【答案】75°
三、解答题
21、
【答案】解:原式=3﹣2×+4﹣(﹣1),
=3﹣+4﹣+1,
=+5.
22、
【答案】解:∵x=(﹣cos60°)﹣1=(﹣)﹣1=﹣2,y=﹣sin30°=﹣,
∴[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy
=[4(x2y2﹣2xy+1)﹣(22﹣x2y2)]
=(4x2y2﹣8xy+4﹣4+x2y2)
=(5x2y2﹣8xy)
=20xy﹣32
=20×(﹣2)×(﹣)﹣32
=﹣12.
23、
【答案】解:原式=÷
=×
=,
当x=3×﹣1=﹣1时,
原式==1﹣.
24、
【答案】解:原式=[
﹣
] (a+1)
=
(a+1)
=
(a+1)
=
(a+1)
=
,
当a=2sin60°+tan45°=2×
+1=
+1时,原式=
=
.
25、
【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB‖CD且AB=CD,
∵E,F分别是AB,CD的中点,
∴AE=AB
,
DF=DC
∴AE=DF,
∴四边形AEFD是平行四边形;
(2)解:过点D作DG⊥AB于点G.
∵AB=2AD=4,
∴AD=2.
在Rt△AGD中,∵∠AGD=90°,∠A=60°,AD=2,
∴AG=AD×cos60°=1
,DG=AD×sin60°=
∴BG=AB-AG=3
在Rt△DGB中,∵∠DGB=90°,DG=,BG=3,
∴BD===
