5.2 平行线及其判定 第2课时同步练习
文档属性
| 名称 | 5.2 平行线及其判定 第2课时同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 421.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 00:00:00 | ||
图片预览


文档简介
5.2 平行线及其判定
第2课时 平行线的判定——利用“同位角、第三直线”
基础训练
知识点1 由“同位角相等”判定两直线平行
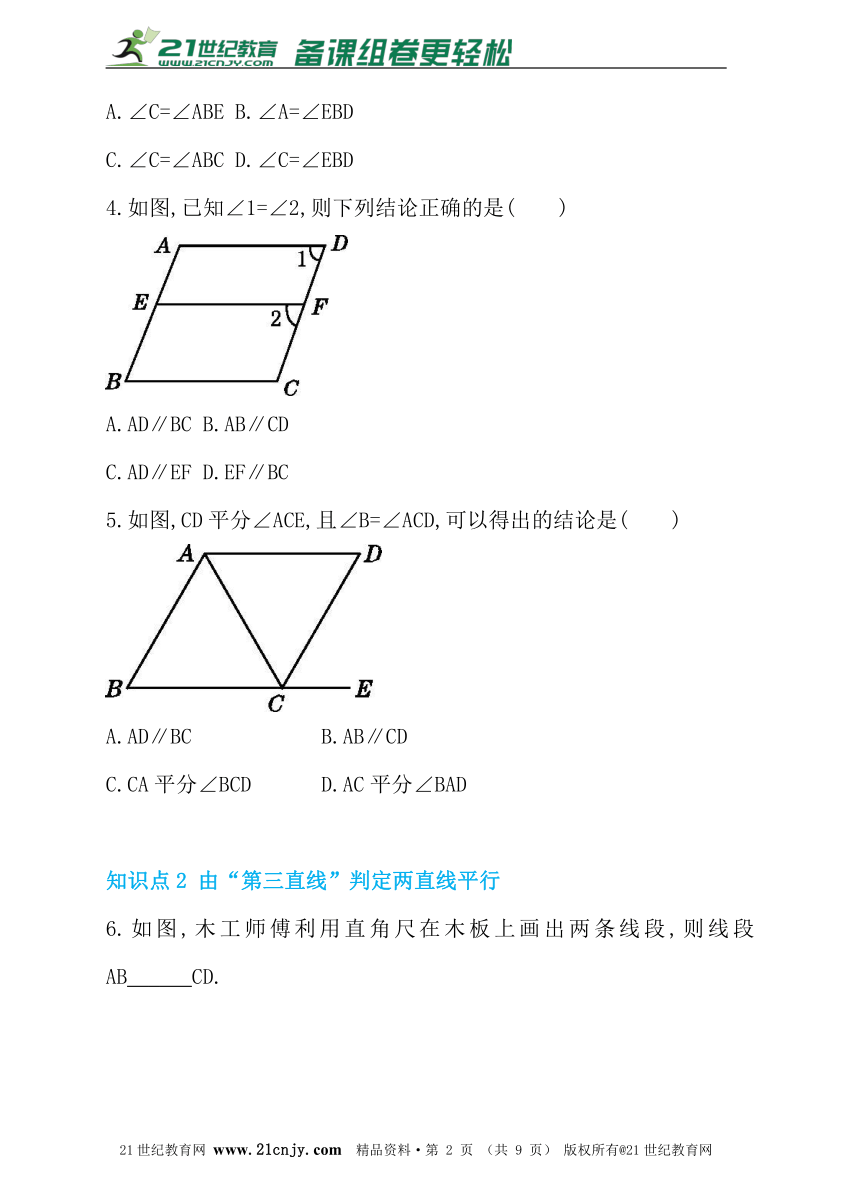
1.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为_______________,理由是______________.
2.如图,直线a,b被直线c所截,下列条件能使a∥b的
是( )
A.∠1=∠6 B.∠2=∠6
C.∠1=∠3 D.∠5=∠7
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠EBD
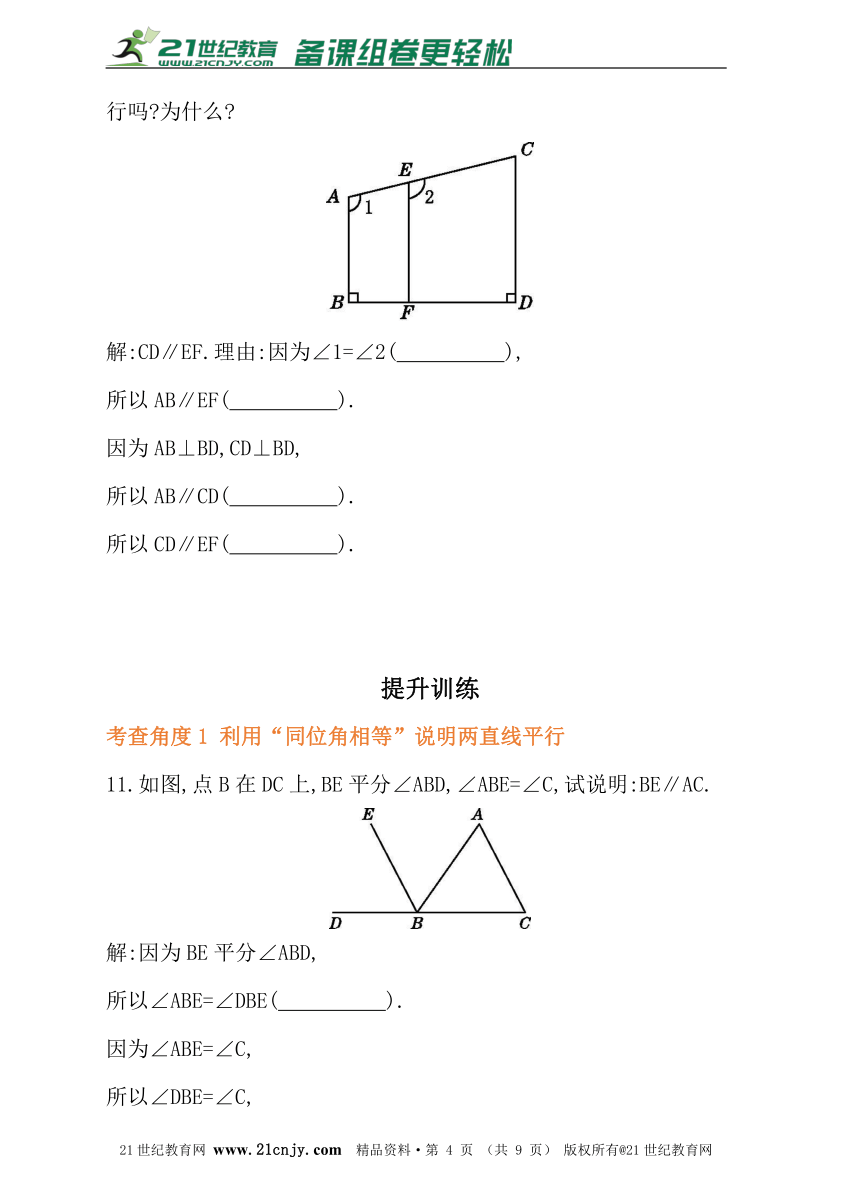
4.如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
5.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD
C.CA平分∠BCD D.AC平分∠BAD
知识点2 由“第三直线”判定两直线平行
6.如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB______CD.
7.在每一步推理后面的括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,
所以AB∥EF(____________).?
(2)如图②,因为AB∥CD,过点F作EF∥AB(____________),?
所以EF∥CD(____________).?
8.在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
9.三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
易错点 填错理由而致错
10.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?
解:CD∥EF.理由:因为∠1=∠2( ),?
所以AB∥EF( ).?
因为AB⊥BD,CD⊥BD,
所以AB∥CD( ).?
所以CD∥EF( ).?
提升训练
考查角度1 利用“同位角相等”说明两直线平行
11.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
解:因为BE平分∠ABD,
所以∠ABE=∠DBE( ).?
因为∠ABE=∠C,
所以∠DBE=∠C,
所以BE∥AC( ).?
12.如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以 ∥ (同位角相等,两直线平行).?
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4,
所以 ∥ (同位角相等,两直线平行).?
考查角度2 利用“同位角”“第三直线”(平行或垂直)判定平行
13.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),?
所以a∥b( ).?
因为∠3=∠4( ),?
所以b∥c( ).?
所以a∥c( ).?
14.如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明.
(2)方法二:用“第三直线”说明.
探究培优
拔尖角度1 利用平行线、垂线的基本事实说明三点共线
15.在同一平面内,已知A,B,C是直线l同旁的三个点.
(1)若AB∥l,BC∥l,则A,B,C三点在同一条直线上吗?为什么?
(2)若AB⊥l,BC⊥l,则A,B,C三点在同一条直线上吗?为什么?
拔尖角度2 利用同位角探究两线段的位置关系
16.如图所示,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,
问:CE与DF的位置关系怎样?试说明理由.
参考答案
1.【答案】AB∥CD;同位角相等,两直线平行
2.【答案】B 3.【答案】D
4.【答案】C
解:找出∠1和∠2是直线AD,EF被直线CD所截而形成的同位角,因此由∠1=∠2可得出AD∥EF.
5.【答案】B 6.【答案】∥
7.【答案】(1)平行于同一条直线的两条直线平行
(2)过直线外一点,有且只有一条直线与这条直线平行;平行于同一条直线的两条直线平行
8.【答案】D
9.【答案】B
解:由平行于同一条直线的两条直线互相平行知选B.
10.已知;同位角相等,两直线平行;在同一平面内,垂直于同一条直线的两条直线互相平行;平行于同一条直线的两条直线互相平行
分析:本题学生容易混淆判定两直线平行的几种方法,从而导致错误.
11.【答案】角平分线的定义;同位角相等,两直线平行
12.【答案】(1)a;b (2)b;c
13.【答案】已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行21世纪教育网版权所有
14.解:(1)方法一:因为∠1=90°,∠2=90°,所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,所以CD⊥AB,EF⊥AB.
所以CD∥EF.
15.解:(1)在同一条直线上.理由:因为直线AB,BC都经过点B,且都与直线l平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上.
(2)在同一条直线上.理由:因为直线AB,BC都经过点B,且都与直线l垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上.
16.解:CE∥DF.理由如下:
因为BD平分∠ABC,CE平分∠ACB,
所以∠DBC=∠ABC,∠BCE=∠ACB.
因为∠ABC=∠ACB,所以∠DBC=∠BCE.
因为∠DBF=∠F,所以∠BCE=∠F,
所以CE∥DF.
第2课时 平行线的判定——利用“同位角、第三直线”
基础训练
知识点1 由“同位角相等”判定两直线平行
1.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为_______________,理由是______________.
2.如图,直线a,b被直线c所截,下列条件能使a∥b的
是( )
A.∠1=∠6 B.∠2=∠6
C.∠1=∠3 D.∠5=∠7
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠EBD
4.如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
5.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD
C.CA平分∠BCD D.AC平分∠BAD
知识点2 由“第三直线”判定两直线平行
6.如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB______CD.
7.在每一步推理后面的括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,
所以AB∥EF(____________).?
(2)如图②,因为AB∥CD,过点F作EF∥AB(____________),?
所以EF∥CD(____________).?
8.在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
9.三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
易错点 填错理由而致错
10.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?
解:CD∥EF.理由:因为∠1=∠2( ),?
所以AB∥EF( ).?
因为AB⊥BD,CD⊥BD,
所以AB∥CD( ).?
所以CD∥EF( ).?
提升训练
考查角度1 利用“同位角相等”说明两直线平行
11.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.
解:因为BE平分∠ABD,
所以∠ABE=∠DBE( ).?
因为∠ABE=∠C,
所以∠DBE=∠C,
所以BE∥AC( ).?
12.如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以 ∥ (同位角相等,两直线平行).?
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4,
所以 ∥ (同位角相等,两直线平行).?
考查角度2 利用“同位角”“第三直线”(平行或垂直)判定平行
13.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),?
所以a∥b( ).?
因为∠3=∠4( ),?
所以b∥c( ).?
所以a∥c( ).?
14.如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明.
(2)方法二:用“第三直线”说明.
探究培优
拔尖角度1 利用平行线、垂线的基本事实说明三点共线
15.在同一平面内,已知A,B,C是直线l同旁的三个点.
(1)若AB∥l,BC∥l,则A,B,C三点在同一条直线上吗?为什么?
(2)若AB⊥l,BC⊥l,则A,B,C三点在同一条直线上吗?为什么?
拔尖角度2 利用同位角探究两线段的位置关系
16.如图所示,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,
问:CE与DF的位置关系怎样?试说明理由.
参考答案
1.【答案】AB∥CD;同位角相等,两直线平行
2.【答案】B 3.【答案】D
4.【答案】C
解:找出∠1和∠2是直线AD,EF被直线CD所截而形成的同位角,因此由∠1=∠2可得出AD∥EF.
5.【答案】B 6.【答案】∥
7.【答案】(1)平行于同一条直线的两条直线平行
(2)过直线外一点,有且只有一条直线与这条直线平行;平行于同一条直线的两条直线平行
8.【答案】D
9.【答案】B
解:由平行于同一条直线的两条直线互相平行知选B.
10.已知;同位角相等,两直线平行;在同一平面内,垂直于同一条直线的两条直线互相平行;平行于同一条直线的两条直线互相平行
分析:本题学生容易混淆判定两直线平行的几种方法,从而导致错误.
11.【答案】角平分线的定义;同位角相等,两直线平行
12.【答案】(1)a;b (2)b;c
13.【答案】已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行21世纪教育网版权所有
14.解:(1)方法一:因为∠1=90°,∠2=90°,所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,所以CD⊥AB,EF⊥AB.
所以CD∥EF.
15.解:(1)在同一条直线上.理由:因为直线AB,BC都经过点B,且都与直线l平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上.
(2)在同一条直线上.理由:因为直线AB,BC都经过点B,且都与直线l垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上.
16.解:CE∥DF.理由如下:
因为BD平分∠ABC,CE平分∠ACB,
所以∠DBC=∠ABC,∠BCE=∠ACB.
因为∠ABC=∠ACB,所以∠DBC=∠BCE.
因为∠DBF=∠F,所以∠BCE=∠F,
所以CE∥DF.
