5.3 平行线的性质 第1课时 平行线的性质 同步练习
文档属性
| 名称 | 5.3 平行线的性质 第1课时 平行线的性质 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 435.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 18:15:01 | ||
图片预览

文档简介
5.3 平行线的性质
第1课时 平行线的性质
基础训练
知识点1 “同位角”的性质
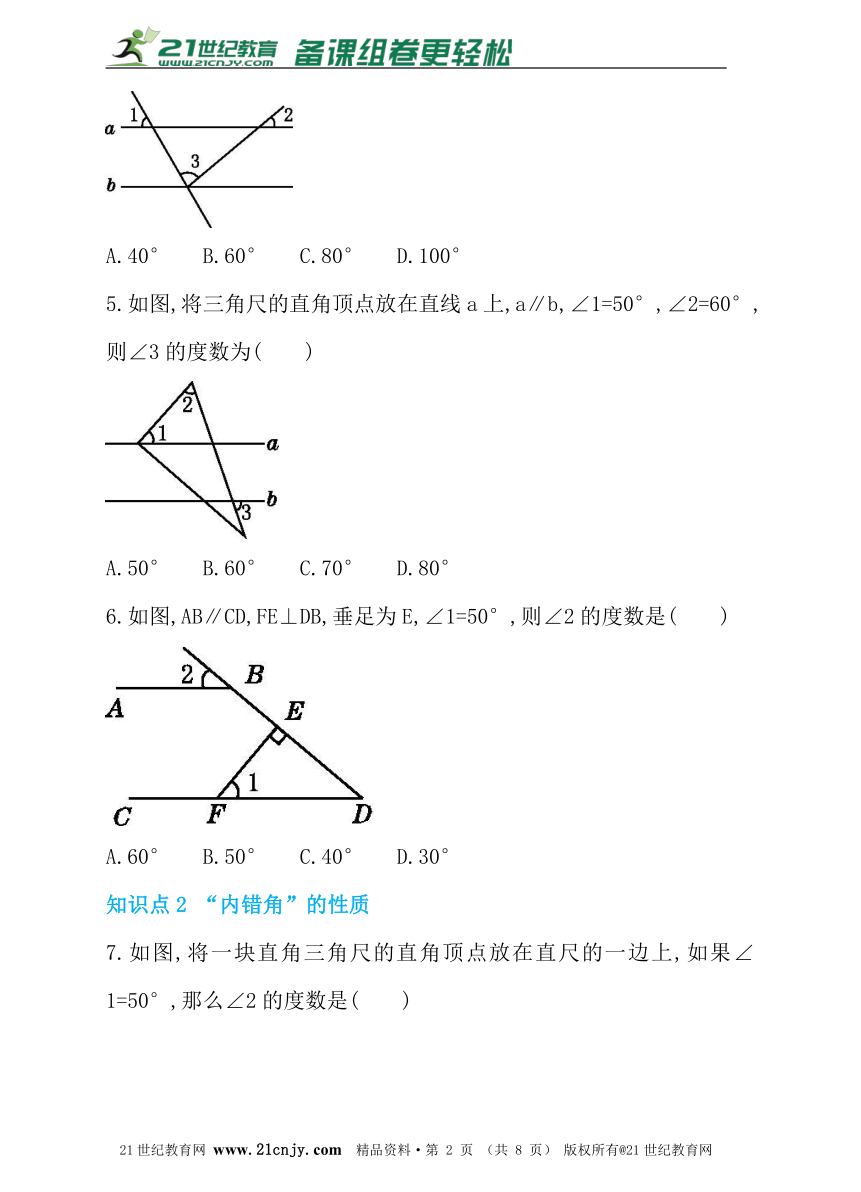
1.如图,直线a∥b,∠1=55°,则∠2=( )
A.35° B.45° C.55° D.65°
2.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
A.50° B.40° C.30° D.25°
3.如图,AB∥CD,∠A=50°,则∠1的大小是( )
A.50° B.120° C.130° D.150°
4.如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
A.40° B.60° C.80° D.100°
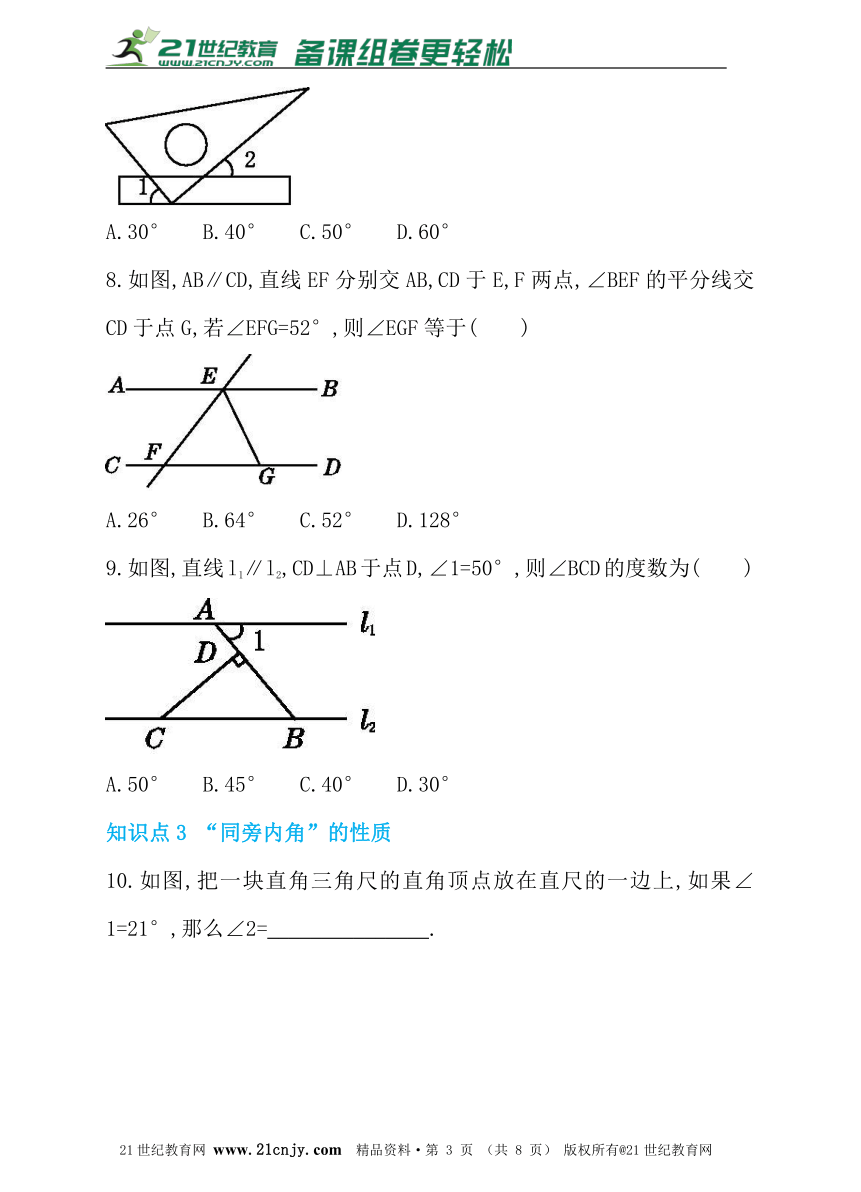
5.如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为( )2·1·c·n·j·y
A.50° B.60° C.70° D.80°
6.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
知识点2 “内错角”的性质
7.如图,将一块直角三角尺的直角顶点放在直尺的一边上,如果∠1=50°,那么∠2的度数是( )
A.30° B.40° C.50° D.60°
8.如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )21·世纪*教育网
A.26° B.64° C.52° D.128°
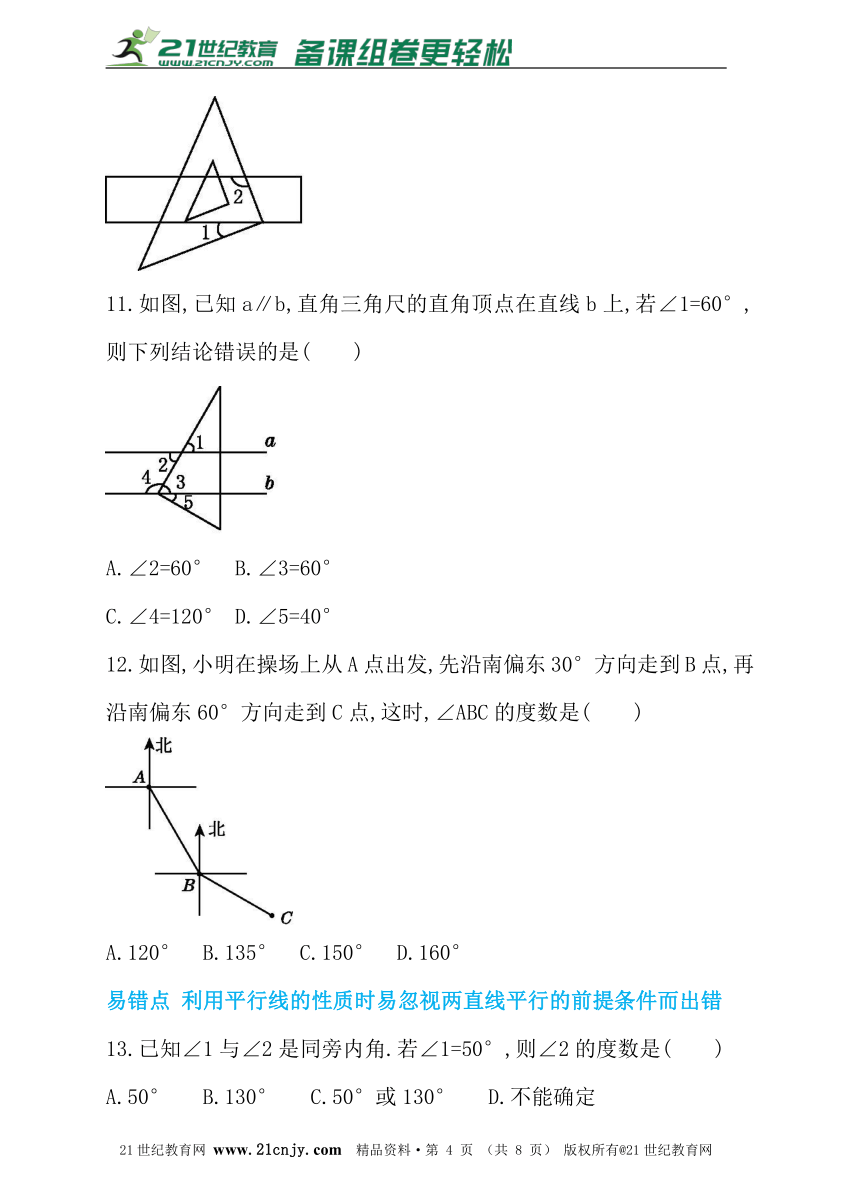
9.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
A.50° B.45° C.40° D.30°
知识点3 “同旁内角”的性质
10.如图,把一块直角三角尺的直角顶点放在直尺的一边上,如果∠1=21°,那么∠2=_______________.?2-1-c-n-j-y
11.如图,已知a∥b,直角三角尺的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
A.∠2=60° B.∠3=60°
C.∠4=120° D.∠5=40°
12.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点,这时,∠ABC的度数是( )
A.120° B.135° C.150° D.160°
易错点 利用平行线的性质时易忽视两直线平行的前提条件而出错
13.已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
提升训练
命题角度1 利用平行线的性质求角
14.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )【来源:21·世纪·教育·网】
A.40° B.70° C.80° D.140°
命题角度2 利用平行线的性质、折叠的特征求角
15.将一张长方形纸片折叠成如图所示的形状,则∠ABC=( )
A.73° B.56° C.68° D.146°
考查角度1 利用平行线的性质求角
16.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
17.如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数. 21cnjy.com
考查角度2 利用平行线的判定和性质说明两直线的位置关系
18.如图所示,已知DE∥BC,且BE,DF分别平分∠ABC,∠ADE,则DF∥BE.请说明理由. www-2-1-cnjy-com
考查角度3 利用平行线的性质解决实际应用问题
(建模思想、补形法)
19.如图是某次考古发掘出的一个四边形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°,已知在四边形中,AD∥BC,请你帮助工作人员求出另外两个角的度数. 21世纪教育网版权所有
参考答案
1.【答案】C 2.【答案】B 3.【答案】C
4.【答案】C 5.【答案】C
6.【答案】C
解:因为FE⊥DB,所以∠FED=90°.所以∠EDF=180°-∠1-∠FED=180°-50°-90°=40°.又因为AB∥CD,所以∠2=∠FDE=40°.故选C.21教育网
7.【答案】B 8.【答案】B 9.【答案】C
10.【答案】111° 11.【答案】D 12.【答案】C
13.【答案】D
解:本题易忽略利用平行线的性质的前提条件而误用平行线的性质.本题没有说明两直线平行,因此同旁内角的数量关系是不确定的.
14.【答案】B 15.【答案】A
16.解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°.∵BC平分∠ABD,∴∠ABD=2∠ABC=130°.∴∠BDC=180°-∠ABD=50°.∴∠2=∠BDC=50°.21·cn·jy·com
17.解:因为DE∥BC,所以∠DOB=∠OBC,∠EOC=∠OCB.
因为BO,CO分别平分∠ABC,∠ACB,
所以∠OBC=∠ABC=20°,∠OCB=∠ACB=30°,
所以∠DOB=20°,∠EOC=30°,
所以∠BOC=180°-∠DOB-∠EOC=130°.
18.解:∵DE∥BC,∴∠ADE=∠ABC.又DF,BE分别平分∠ADE,∠ABC,∴∠ADF=∠ADE,∠ABE=∠ABC,∴∠ADF=∠ABE,∴DF∥BE.
19.解:因为AD∥BC(已知),所以∠A+∠B=180°,∠C+∠D=180°(两直线平行,同旁内角互补).所以∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-110°=70°.www.21-cn-jy.com
分析:此题把实际问题转化成数学问题,利用所学的几何知识来解决.体现了建模思想的应用.
第1课时 平行线的性质
基础训练
知识点1 “同位角”的性质
1.如图,直线a∥b,∠1=55°,则∠2=( )
A.35° B.45° C.55° D.65°
2.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
A.50° B.40° C.30° D.25°
3.如图,AB∥CD,∠A=50°,则∠1的大小是( )
A.50° B.120° C.130° D.150°
4.如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
A.40° B.60° C.80° D.100°
5.如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为( )2·1·c·n·j·y
A.50° B.60° C.70° D.80°
6.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
知识点2 “内错角”的性质
7.如图,将一块直角三角尺的直角顶点放在直尺的一边上,如果∠1=50°,那么∠2的度数是( )
A.30° B.40° C.50° D.60°
8.如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )21·世纪*教育网
A.26° B.64° C.52° D.128°
9.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
A.50° B.45° C.40° D.30°
知识点3 “同旁内角”的性质
10.如图,把一块直角三角尺的直角顶点放在直尺的一边上,如果∠1=21°,那么∠2=_______________.?2-1-c-n-j-y
11.如图,已知a∥b,直角三角尺的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
A.∠2=60° B.∠3=60°
C.∠4=120° D.∠5=40°
12.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点,这时,∠ABC的度数是( )
A.120° B.135° C.150° D.160°
易错点 利用平行线的性质时易忽视两直线平行的前提条件而出错
13.已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
提升训练
命题角度1 利用平行线的性质求角
14.如图,直线AB∥CD,AE平分∠CAB,AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )【来源:21·世纪·教育·网】
A.40° B.70° C.80° D.140°
命题角度2 利用平行线的性质、折叠的特征求角
15.将一张长方形纸片折叠成如图所示的形状,则∠ABC=( )
A.73° B.56° C.68° D.146°
考查角度1 利用平行线的性质求角
16.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
17.如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC,求∠BOC的度数. 21cnjy.com
考查角度2 利用平行线的判定和性质说明两直线的位置关系
18.如图所示,已知DE∥BC,且BE,DF分别平分∠ABC,∠ADE,则DF∥BE.请说明理由. www-2-1-cnjy-com
考查角度3 利用平行线的性质解决实际应用问题
(建模思想、补形法)
19.如图是某次考古发掘出的一个四边形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°,已知在四边形中,AD∥BC,请你帮助工作人员求出另外两个角的度数. 21世纪教育网版权所有
参考答案
1.【答案】C 2.【答案】B 3.【答案】C
4.【答案】C 5.【答案】C
6.【答案】C
解:因为FE⊥DB,所以∠FED=90°.所以∠EDF=180°-∠1-∠FED=180°-50°-90°=40°.又因为AB∥CD,所以∠2=∠FDE=40°.故选C.21教育网
7.【答案】B 8.【答案】B 9.【答案】C
10.【答案】111° 11.【答案】D 12.【答案】C
13.【答案】D
解:本题易忽略利用平行线的性质的前提条件而误用平行线的性质.本题没有说明两直线平行,因此同旁内角的数量关系是不确定的.
14.【答案】B 15.【答案】A
16.解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°.∵BC平分∠ABD,∴∠ABD=2∠ABC=130°.∴∠BDC=180°-∠ABD=50°.∴∠2=∠BDC=50°.21·cn·jy·com
17.解:因为DE∥BC,所以∠DOB=∠OBC,∠EOC=∠OCB.
因为BO,CO分别平分∠ABC,∠ACB,
所以∠OBC=∠ABC=20°,∠OCB=∠ACB=30°,
所以∠DOB=20°,∠EOC=30°,
所以∠BOC=180°-∠DOB-∠EOC=130°.
18.解:∵DE∥BC,∴∠ADE=∠ABC.又DF,BE分别平分∠ADE,∠ABC,∴∠ADF=∠ADE,∠ABE=∠ABC,∴∠ADF=∠ABE,∴DF∥BE.
19.解:因为AD∥BC(已知),所以∠A+∠B=180°,∠C+∠D=180°(两直线平行,同旁内角互补).所以∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-110°=70°.www.21-cn-jy.com
分析:此题把实际问题转化成数学问题,利用所学的几何知识来解决.体现了建模思想的应用.
