第六章 第一节 平行四边形的性质 课时1同步练习
文档属性
| 名称 | 第六章 第一节 平行四边形的性质 课时1同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 22:18:42 | ||
图片预览


文档简介
第一节 平行四边形的性质
第1课时 平行四边形的边、角性质
基础检测
知识点1平行四边形的定义
1.两组对边分别_________的四边形叫做平行四边形.平行四边形ABCD记作“_________”,它包含两层意义:? _________
或________??
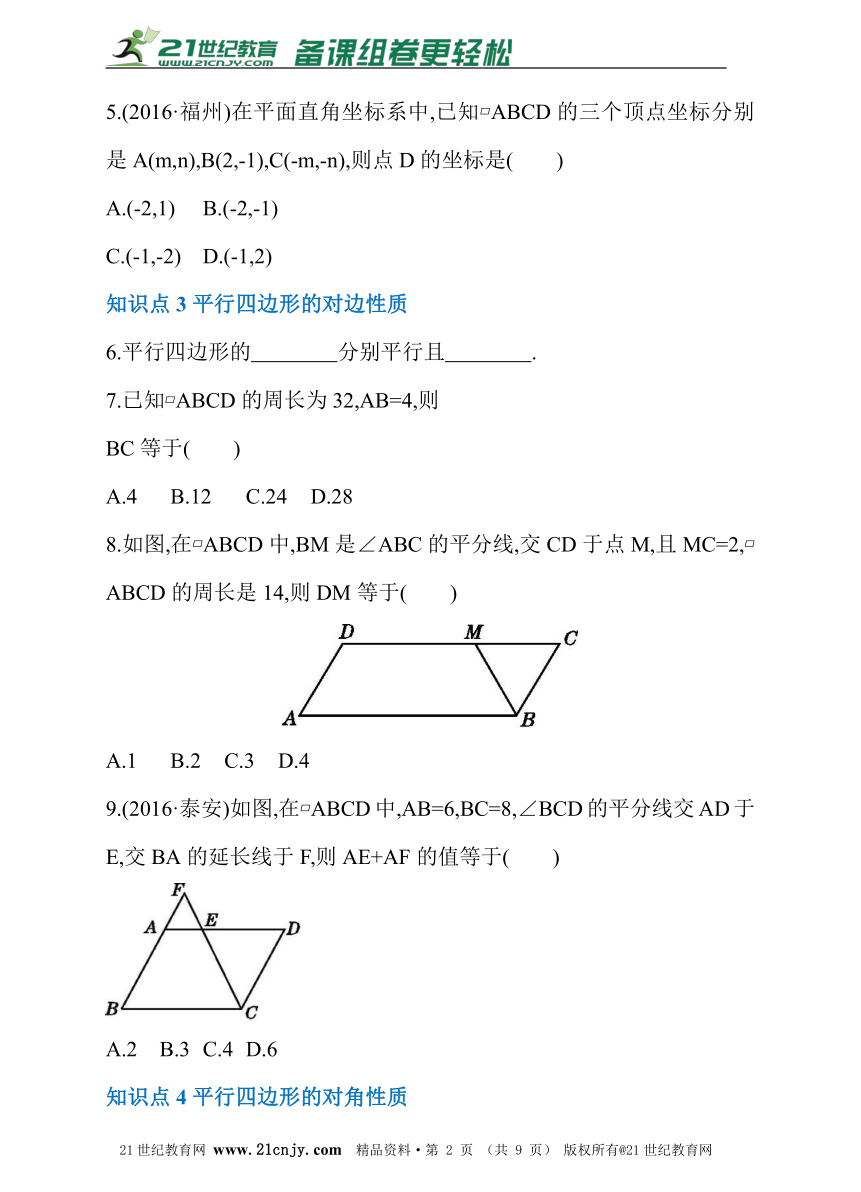
2.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是_________.?
3.如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A.8个 B.9个 C.7个 D.5个
知识点2平行四边形的对称性
4.平行四边形是中心对称图形,两条对角线的交点是它
的_________.?
5.(2016·福州)在平面直角坐标系中,已知?ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )21教育网
A.(-2,1) B.(-2,-1)
C.(-1,-2) D.(-1,2)
知识点3平行四边形的对边性质
6.平行四边形的 分别平行且 .?
7.已知?ABCD的周长为32,AB=4,则
BC等于( )
A.4 B.12 C.24 D.28
8.如图,在?ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )21cnjy.com
A.1 B.2 C.3 D.4
9.(2016·泰安)如图,在?ABCD中,AB=6,BC=8,∠BCD的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )www.21-cn-jy.com
A.2 B.3 C.4 D.6
知识点4平行四边形的对角性质
10.平行四边形的对角_________,邻角_________.?
11.已知在?ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160°
C.80° D.60°
12.如图,在?ABCD中,CE⊥AB,E为垂足,如果∠A=
120°,那么∠BCE的度数是( )
A.80° B.50° C.40° D.30°
13.如图,在?ABCD中,E,F是对角线BD上的两点,若添加一个条件,使△ABE≌△CDF,则添加的条件不能为( ) 【来源:21·世纪·教育·网】
A.BE=DF B.BF=DE
C.AE=CF D.∠1=∠2
培优检测
题型1平行四边形的定义在证边相等中的应用
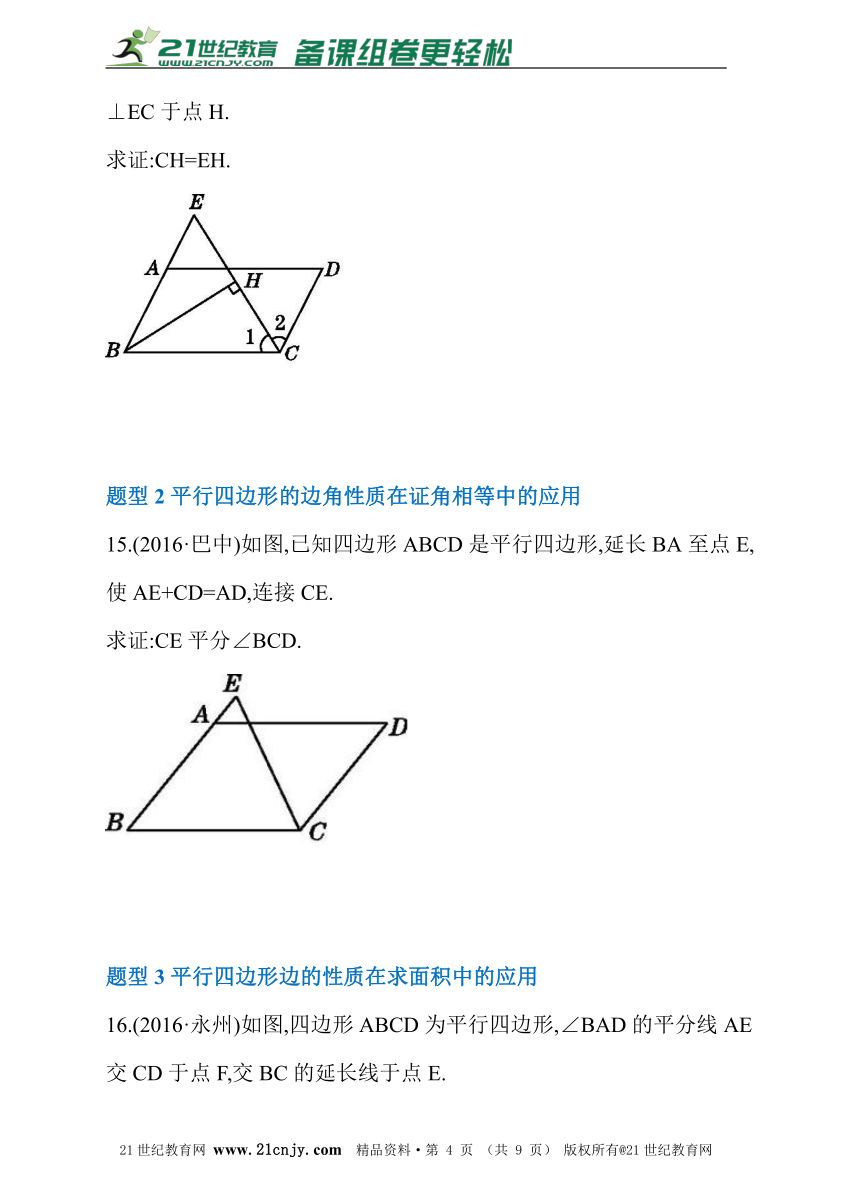
14.如图,在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H.
求证:CH=EH.
题型2平行四边形的边角性质在证角相等中的应用
15.(2016·巴中)如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD,连接CE.21·cn·jy·com
求证:CE平分∠BCD.
题型3平行四边形边的性质在求面积中的应用
16.(2016·永州)如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E.2·1·c·n·j·y
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求?ABCD的面积.
题型4平行四边形的边角性质在求边长中的应用
17.(2016·温州)如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
18.如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由. 21·世纪*教育网
参考答案
1.【答案】平行;?ABCD;?ABCD;?ABCD
2.【答案】平行四边形
3.【答案】B
4.【答案】对称中心
5.【答案】A
6.【答案】对边;相等
7.【答案】B 8.【答案】C 9.【答案】C
10.【答案】相等;互补
11.【答案】C 12.【答案】D 13.【答案】C
14.证明:∵在?ABCD中,BE∥CD,∴∠E=∠2.
∵CE平分∠BCD,∴∠1=∠2.
∴∠1=∠E.∴BE=BC.
又∵BH⊥EC,∴CH=EH.
15.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠E=∠ECD,AB=CD.
∴AE+AB=AD=BC.∴BE=BC.
∴∠E=∠ECB.∴∠ECD=∠ECB,即CE平分∠BCD.
16.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAE=∠E.
又∵AE平分∠BAD,∴∠BAE=∠DAE.∴∠BAE=∠E.
∴BA=BE=CD.
(2)解:∵∠BEA=60°,BA=BE,∴△ABE为等边三角形.
∵BF⊥AE,∴F为AE的中点.
在△AFD和△EFC中,
∴△AFD≌△EFC(ASA).
∴△AFD的面积等于△EFC的面积.
∴?ABCD的面积等于△ABE的面积.
在△ABE中,AB=AE=4,
∴AF=2.由勾股定理得BF=2,
∴△ABE的面积=×4×2=4.
∴?ABCD的面积为4.
17.(1)证明:在?ABCD中,AD∥BC,
∴∠D=∠DCF.
在△ADE和△FCE中,
∴△ADE≌△FCE(ASA).
(2)解:由(1)知△ADE≌△FCE,∴AD=CF=BC=5,
EF=AE=3.
∴BF=10,AF=6.
在Rt△BAF中,AB==8,∴CD=AB=8.
18.解:EF+GH+MN=2a,EF+GH+MN的值不随点P位置的改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵GH∥BC,∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形,∴GH=AG=AM+MG.①
同理△BMN是等边三角形,
∴MN=MB=MG+GB.②
∵MN∥AC,EF∥AB,∴四边形AMPE是平行四边形,
∴PE=AM.
同理可证四边形BFPG是平行四边形,∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得
EF+GH+MN=(AM+GB)+(AM+MG)+(MG+GB)=2(AM+MG+GB)=2AB=2a.21世纪教育网版权所有
第1课时 平行四边形的边、角性质
基础检测
知识点1平行四边形的定义
1.两组对边分别_________的四边形叫做平行四边形.平行四边形ABCD记作“_________”,它包含两层意义:? _________
或________??
2.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是_________.?
3.如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A.8个 B.9个 C.7个 D.5个
知识点2平行四边形的对称性
4.平行四边形是中心对称图形,两条对角线的交点是它
的_________.?
5.(2016·福州)在平面直角坐标系中,已知?ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )21教育网
A.(-2,1) B.(-2,-1)
C.(-1,-2) D.(-1,2)
知识点3平行四边形的对边性质
6.平行四边形的 分别平行且 .?
7.已知?ABCD的周长为32,AB=4,则
BC等于( )
A.4 B.12 C.24 D.28
8.如图,在?ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )21cnjy.com
A.1 B.2 C.3 D.4
9.(2016·泰安)如图,在?ABCD中,AB=6,BC=8,∠BCD的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )www.21-cn-jy.com
A.2 B.3 C.4 D.6
知识点4平行四边形的对角性质
10.平行四边形的对角_________,邻角_________.?
11.已知在?ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160°
C.80° D.60°
12.如图,在?ABCD中,CE⊥AB,E为垂足,如果∠A=
120°,那么∠BCE的度数是( )
A.80° B.50° C.40° D.30°
13.如图,在?ABCD中,E,F是对角线BD上的两点,若添加一个条件,使△ABE≌△CDF,则添加的条件不能为( ) 【来源:21·世纪·教育·网】
A.BE=DF B.BF=DE
C.AE=CF D.∠1=∠2
培优检测
题型1平行四边形的定义在证边相等中的应用
14.如图,在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H.
求证:CH=EH.
题型2平行四边形的边角性质在证角相等中的应用
15.(2016·巴中)如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD,连接CE.21·cn·jy·com
求证:CE平分∠BCD.
题型3平行四边形边的性质在求面积中的应用
16.(2016·永州)如图,四边形ABCD为平行四边形,∠BAD的平分线AE交CD于点F,交BC的延长线于点E.2·1·c·n·j·y
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求?ABCD的面积.
题型4平行四边形的边角性质在求边长中的应用
17.(2016·温州)如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
18.如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由. 21·世纪*教育网
参考答案
1.【答案】平行;?ABCD;?ABCD;?ABCD
2.【答案】平行四边形
3.【答案】B
4.【答案】对称中心
5.【答案】A
6.【答案】对边;相等
7.【答案】B 8.【答案】C 9.【答案】C
10.【答案】相等;互补
11.【答案】C 12.【答案】D 13.【答案】C
14.证明:∵在?ABCD中,BE∥CD,∴∠E=∠2.
∵CE平分∠BCD,∴∠1=∠2.
∴∠1=∠E.∴BE=BC.
又∵BH⊥EC,∴CH=EH.
15.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠E=∠ECD,AB=CD.
∴AE+AB=AD=BC.∴BE=BC.
∴∠E=∠ECB.∴∠ECD=∠ECB,即CE平分∠BCD.
16.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAE=∠E.
又∵AE平分∠BAD,∴∠BAE=∠DAE.∴∠BAE=∠E.
∴BA=BE=CD.
(2)解:∵∠BEA=60°,BA=BE,∴△ABE为等边三角形.
∵BF⊥AE,∴F为AE的中点.
在△AFD和△EFC中,
∴△AFD≌△EFC(ASA).
∴△AFD的面积等于△EFC的面积.
∴?ABCD的面积等于△ABE的面积.
在△ABE中,AB=AE=4,
∴AF=2.由勾股定理得BF=2,
∴△ABE的面积=×4×2=4.
∴?ABCD的面积为4.
17.(1)证明:在?ABCD中,AD∥BC,
∴∠D=∠DCF.
在△ADE和△FCE中,
∴△ADE≌△FCE(ASA).
(2)解:由(1)知△ADE≌△FCE,∴AD=CF=BC=5,
EF=AE=3.
∴BF=10,AF=6.
在Rt△BAF中,AB==8,∴CD=AB=8.
18.解:EF+GH+MN=2a,EF+GH+MN的值不随点P位置的改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵GH∥BC,∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形,∴GH=AG=AM+MG.①
同理△BMN是等边三角形,
∴MN=MB=MG+GB.②
∵MN∥AC,EF∥AB,∴四边形AMPE是平行四边形,
∴PE=AM.
同理可证四边形BFPG是平行四边形,∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得
EF+GH+MN=(AM+GB)+(AM+MG)+(MG+GB)=2(AM+MG+GB)=2AB=2a.21世纪教育网版权所有
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
