5.3 平行线的判定和性质的综合应用 同步练习
文档属性
| 名称 | 5.3 平行线的判定和性质的综合应用 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 475.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:03:55 | ||
图片预览


文档简介
5.3 平行线的性质
第2课时 平行线的判定和性质的综合应用
基础训练
知识点1 平行线的性质的应用
1.如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35° B.40° C.45° D.50°
2.(2016·遵义)如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
A.90° B.85° C.80° D.60°
3.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
A.70° B.60° C.55° D.50°
4.(2016·湖州改编)如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是_________度.2·1·c·n·j·y
5.一个人从A地出发向北偏东60°方向走了一段距离到B地,再从B地出发,向南偏西15°方向走了一段距离到达C地,则∠ABC的度数是________.?【来源:21·世纪·教育·网】
知识点2 平行线的判定的应用
6.如图,已知BE平分∠ABC,CF平分∠BCD,∠1=∠2,那么直线AB与CD的位置关系是________.21·世纪*教育网
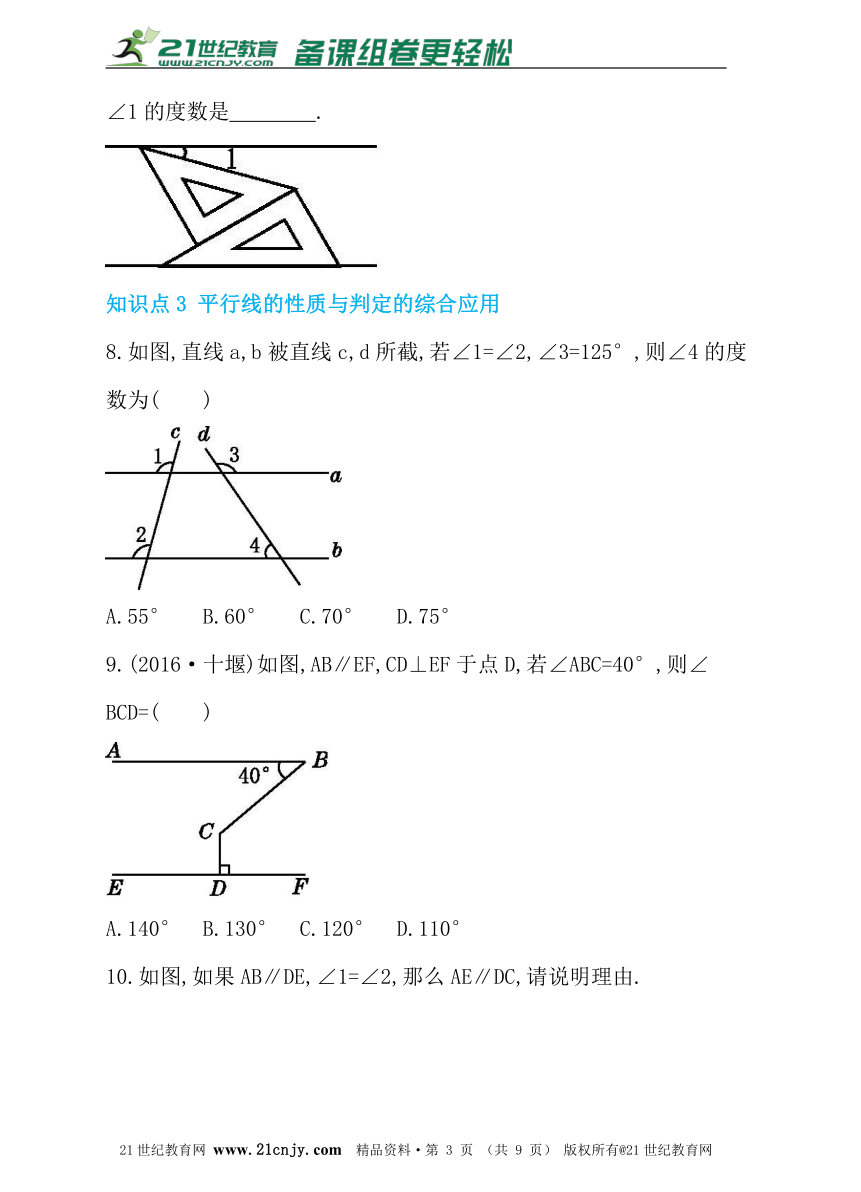
7.(2016·菏泽)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .?www-2-1-cnjy-com
知识点3 平行线的性质与判定的综合应用
8.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度
数为( )
A.55° B.60° C.70° D.75°
9.(2016·十堰)如图,AB∥EF,CD⊥EF于点D,若∠ABC=40°,则∠
BCD=( )
A.140° B.130° C.120° D.110°
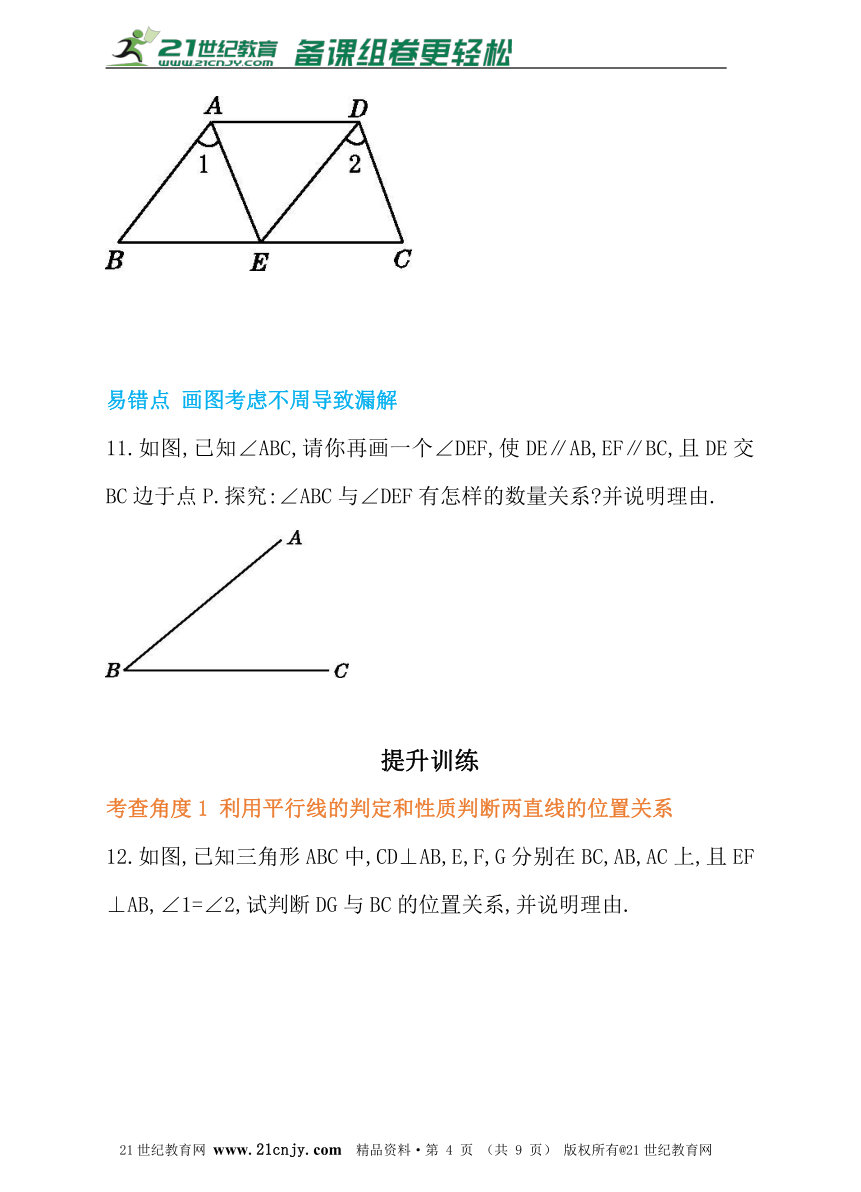
10.如图,如果AB∥DE,∠1=∠2,那么AE∥DC,请说明理由.
易错点 画图考虑不周导致漏解
11.如图,已知∠ABC,请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边于点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
提升训练
考查角度1 利用平行线的判定和性质判断两直线的位置关系
12.如图,已知三角形ABC中,CD⊥AB,E,F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
考查角度2 利用平行线的判定和性质说明角的关系
13.如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD是∠BAC的平分线吗?若是,请说明理由.21世纪教育网版权所有
探究培优
拔尖角度1 利用平行线的判定与性质解决阅读探究问题
14.阅读下列解题过程,然后解答后面的问题.
如图①,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:如图①,过点E作EF∥AB.
则AB∥CD∥EF(平行公理的推论).
∵AB∥EF,∴∠1=∠B=35°.
∵CD∥EF,∴∠2=∠D=32°.
∴∠BED=∠1+∠2=35°+32°=67°.
如图②③,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决.
(1)如图②,已知∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A应多大?
(2)如图③,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?
拔尖角度2 利用平行线与方位角解决实际应用问题
15.如图,A,B两岛位于东西方向的一条水平线上,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,求∠ACB的度数.
参考答案
1.【答案】B 2.【答案】A
3.【答案】A
解:如图,过点E作EF∥AB,此时EF∥CD.∴∠1=∠BEF,∠DEF=∠2,∴∠3=∠BEF+∠DEF=∠1+∠2=70°.21教育网
4.【答案】90 5.【答案】45° 6.【答案】平行
7.【答案】15° 8.【答案】A
9.【答案】B
解:如图,过点C作CG∥AB,
由题意可得AB∥EF∥CG,
故∠B=∠BCG,∠GCD=90°,
则∠BCD=40°+90°=130°.
10.解:∵AB∥DE,∴∠1=∠AED.
又∵∠1=∠2,∴∠AED=∠2.∴AE∥DC.
11.解:画图如图①②③④所示.∠ABC与∠DEF相等或互补,理由如下:如图①,∵AB∥DE,∴∠ABC=∠DPC.∵BC∥EF,∴∠DEF=∠DPC.∴∠
ABC=∠DEF.
如图②,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC=∠DEF.∴∠
ABC=∠DEF.
如图③,∵AB∥DE,∴∠ABC=∠BPE.∵BC∥EF,∴∠DEF+∠BPE=180°.
∴∠ABC+∠DEF=180°.
如图④,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC+∠DEF=180°.
∴∠ABC+∠DEF=180°.
综上可知,∠ABC与∠DEF相等或互补.
分析:本题易错之处在于学生往往只考虑到其中两种情况,而漏掉另外两种情况.
12.解:DG∥BC.理由如下:
∵CD⊥AB,EF⊥AB,∴CD∥EF.
∴∠1=∠DCB.
又∵∠1=∠2,∴∠2=∠DCB,∴DG∥BC.
13.解:AD是∠BAC的平分线.理由如下:
∵AD⊥BC,EG⊥BC,∴EG∥AD.
∴∠3=∠1,∠E=∠2.又∵∠E=∠3,∴∠1=∠2,即AD是∠BAC的平分线.
14.解:(1)如图①,过点C作CF∥DE,则∠2=∠D=30°.因为∠ACD=65°,即∠1+∠2=65°,所以∠1=65°-∠2=65°-30°=35°.因为AB∥DE,CF∥DE,所以AB∥CF,所以∠A=∠1=35°.21cnjy.com
(2)如图②,过点F作FI∥GP,则∠G+∠1=180°.因为GP∥HQ,FI∥GP,所以HQ∥FI.所以∠2+∠H=180°,所以∠G+∠1+∠2+∠H=360°,即∠G+∠GFH+∠H=360°.21·cn·jy·com
15.解:如图,过点A,C,B分别画出南北方向的方向线,由题意,得∠EAC=50°,∠FBC=40°.∵AE∥DC∥BF,∴∠ACD=∠EAC=50°,∠BCD=∠FBC=40°.∴∠ACB=∠ACD+∠BCD=50°+40°=90°.www.21-cn-jy.com
分析:涉及方位角的问题时,一定要画出相应的方向线,同一方向的方向线是彼此平行的,可以直接利用
第2课时 平行线的判定和性质的综合应用
基础训练
知识点1 平行线的性质的应用
1.如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35° B.40° C.45° D.50°
2.(2016·遵义)如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b上,则∠1+∠2的值为( )
A.90° B.85° C.80° D.60°
3.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
A.70° B.60° C.55° D.50°
4.(2016·湖州改编)如图是我们常用的折叠式小刀,刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是_________度.2·1·c·n·j·y
5.一个人从A地出发向北偏东60°方向走了一段距离到B地,再从B地出发,向南偏西15°方向走了一段距离到达C地,则∠ABC的度数是________.?【来源:21·世纪·教育·网】
知识点2 平行线的判定的应用
6.如图,已知BE平分∠ABC,CF平分∠BCD,∠1=∠2,那么直线AB与CD的位置关系是________.21·世纪*教育网
7.(2016·菏泽)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .?www-2-1-cnjy-com
知识点3 平行线的性质与判定的综合应用
8.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度
数为( )
A.55° B.60° C.70° D.75°
9.(2016·十堰)如图,AB∥EF,CD⊥EF于点D,若∠ABC=40°,则∠
BCD=( )
A.140° B.130° C.120° D.110°
10.如图,如果AB∥DE,∠1=∠2,那么AE∥DC,请说明理由.
易错点 画图考虑不周导致漏解
11.如图,已知∠ABC,请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边于点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
提升训练
考查角度1 利用平行线的判定和性质判断两直线的位置关系
12.如图,已知三角形ABC中,CD⊥AB,E,F,G分别在BC,AB,AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
考查角度2 利用平行线的判定和性质说明角的关系
13.如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD是∠BAC的平分线吗?若是,请说明理由.21世纪教育网版权所有
探究培优
拔尖角度1 利用平行线的判定与性质解决阅读探究问题
14.阅读下列解题过程,然后解答后面的问题.
如图①,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数.
解:如图①,过点E作EF∥AB.
则AB∥CD∥EF(平行公理的推论).
∵AB∥EF,∴∠1=∠B=35°.
∵CD∥EF,∴∠2=∠D=32°.
∴∠BED=∠1+∠2=35°+32°=67°.
如图②③,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决.
(1)如图②,已知∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A应多大?
(2)如图③,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?
拔尖角度2 利用平行线与方位角解决实际应用问题
15.如图,A,B两岛位于东西方向的一条水平线上,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,求∠ACB的度数.
参考答案
1.【答案】B 2.【答案】A
3.【答案】A
解:如图,过点E作EF∥AB,此时EF∥CD.∴∠1=∠BEF,∠DEF=∠2,∴∠3=∠BEF+∠DEF=∠1+∠2=70°.21教育网
4.【答案】90 5.【答案】45° 6.【答案】平行
7.【答案】15° 8.【答案】A
9.【答案】B
解:如图,过点C作CG∥AB,
由题意可得AB∥EF∥CG,
故∠B=∠BCG,∠GCD=90°,
则∠BCD=40°+90°=130°.
10.解:∵AB∥DE,∴∠1=∠AED.
又∵∠1=∠2,∴∠AED=∠2.∴AE∥DC.
11.解:画图如图①②③④所示.∠ABC与∠DEF相等或互补,理由如下:如图①,∵AB∥DE,∴∠ABC=∠DPC.∵BC∥EF,∴∠DEF=∠DPC.∴∠
ABC=∠DEF.
如图②,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC=∠DEF.∴∠
ABC=∠DEF.
如图③,∵AB∥DE,∴∠ABC=∠BPE.∵BC∥EF,∴∠DEF+∠BPE=180°.
∴∠ABC+∠DEF=180°.
如图④,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC+∠DEF=180°.
∴∠ABC+∠DEF=180°.
综上可知,∠ABC与∠DEF相等或互补.
分析:本题易错之处在于学生往往只考虑到其中两种情况,而漏掉另外两种情况.
12.解:DG∥BC.理由如下:
∵CD⊥AB,EF⊥AB,∴CD∥EF.
∴∠1=∠DCB.
又∵∠1=∠2,∴∠2=∠DCB,∴DG∥BC.
13.解:AD是∠BAC的平分线.理由如下:
∵AD⊥BC,EG⊥BC,∴EG∥AD.
∴∠3=∠1,∠E=∠2.又∵∠E=∠3,∴∠1=∠2,即AD是∠BAC的平分线.
14.解:(1)如图①,过点C作CF∥DE,则∠2=∠D=30°.因为∠ACD=65°,即∠1+∠2=65°,所以∠1=65°-∠2=65°-30°=35°.因为AB∥DE,CF∥DE,所以AB∥CF,所以∠A=∠1=35°.21cnjy.com
(2)如图②,过点F作FI∥GP,则∠G+∠1=180°.因为GP∥HQ,FI∥GP,所以HQ∥FI.所以∠2+∠H=180°,所以∠G+∠1+∠2+∠H=360°,即∠G+∠GFH+∠H=360°.21·cn·jy·com
15.解:如图,过点A,C,B分别画出南北方向的方向线,由题意,得∠EAC=50°,∠FBC=40°.∵AE∥DC∥BF,∴∠ACD=∠EAC=50°,∠BCD=∠FBC=40°.∴∠ACB=∠ACD+∠BCD=50°+40°=90°.www.21-cn-jy.com
分析:涉及方位角的问题时,一定要画出相应的方向线,同一方向的方向线是彼此平行的,可以直接利用
