四川省成都市龙泉驿区第一中学校高二下学期入学考试数学(理)试题 Word版含答案
文档属性
| 名称 | 四川省成都市龙泉驿区第一中学校高二下学期入学考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 271.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-18 21:06:40 | ||
图片预览




文档简介
成都龙泉中学2016~2017学年度下学期入学考试
高二数学(理科)试卷
本试卷分第I卷(选择题)和第II卷,共4页,满分150分,考试时间120分钟.
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题纸上.
2.考生作答时,请将答案答在答题纸上,在本试卷上答题无效.按照题号在各题的答题区域内作答,超出答题区域书写的答案无效.
3.答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚(选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号).
4.保持答题纸纸面清洁,不破损.考试结束后,将本试卷自行保存,答题纸交回.
第I卷(选择题
共60分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若集合,且,则集合B可能是
A.
B.
C.
D.R
2.已知命题p: x0∈,x+1<0,则
A. p: x∈,x2+1>0
B. p: x∈,x2+1>0
C. p: x∈,x2+1≥0
D. p: x∈,x2+1≥0
3.点在边长为1的正方形内运动,则动点到顶点的距离的概率为
A.
B.
C.
D.
4.设数列的通项公式,其前项和为,则
A.
B.
C.
D.
5.
已知一个几何体的三视图如图所示,则该几何体的体积为
B.
C.
D.2
6.
已知,若,则
A.
B.
C.
D.
7.
已知分别为双曲线的左、右顶点,
是上一点,且直线的斜率之积为,则的离心率为
A.
B.
C.
D.
8.
已知程序框图如图所示,则该程序框图的功能是
A.求数列的前10项和
B.求数列的前10项和
C.求数列的前11项和
D.求数列的前11项和
9.设球的半径为时间t的函数,若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径
A.
成正比,比例系数为C
B.
成正比,比例系数为2C
C.成反比,比例系数为C
D.
成反比,比例系数为2C
10.在四棱锥中,底面是边长为2的菱形,,对角线AC与BD相交于点O,平面,PB与平面所成角为,若E是PB的中点,则异面直线DE与PA所成角的余弦值为
A.
B.
C.
D.
11.
已知定义在上的函数(为实数)为偶函数,记
,则
的大小关系为
A.
B.
C.
D.
12.过抛物线的焦点F作两条相互垂直的射线,分别与抛物线相交于点M,N,过弦MN的中点P作抛物线准线的垂线PQ,垂足为Q,则的最大值为
A.
B.
C.
D.
第Ⅱ卷
非选择题(共90分)
二、填空题(本大题共4小题,每小题5分,满分20分.)
13.
已知向量,若⊥,则
14.
若正数,满足,则的最小值为_________.
15.人造地球卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为,卫星近地点、远地点离地面的距离分别为,则卫星轨道的离心率
.(请用表示)
16.
设分别是双曲线的左、右焦点,A为双曲线的左顶点,以线段为直径的圆O与双曲线的一个交点为P,与轴交于B,D两点,且与双曲线的一条渐近线交于M,N两点,则下列命题正确的是
.(写出所有正确的命题编号)
①线段BD是双曲线的虚轴;②的面积为;
③若,则双曲线C的离心率为;④的内切圆的圆心到轴的距离为.
三、解答题(本部分共计6小题,满分70分.解答应写出文字说明,证明过程或演算步骤,请在指定区域内作答,否则该题计为零分.)
17.(本小题满分10分)
在中,角,,所对的边分别为,,,且,.
(1)若,求的值;
(2)若的面积,求,的值.
18.(本题满分12分)
设数列满足:,.
(1)证明:数列为等比数列,并求出数列的通项公式;
(2)求数列的前项和.
19.(本小题满分12分)
已知双曲线与椭圆共焦点,且它们的离心率之和为,求双曲线的标准方程及其渐进线方程.
20.
(本题满分12分)
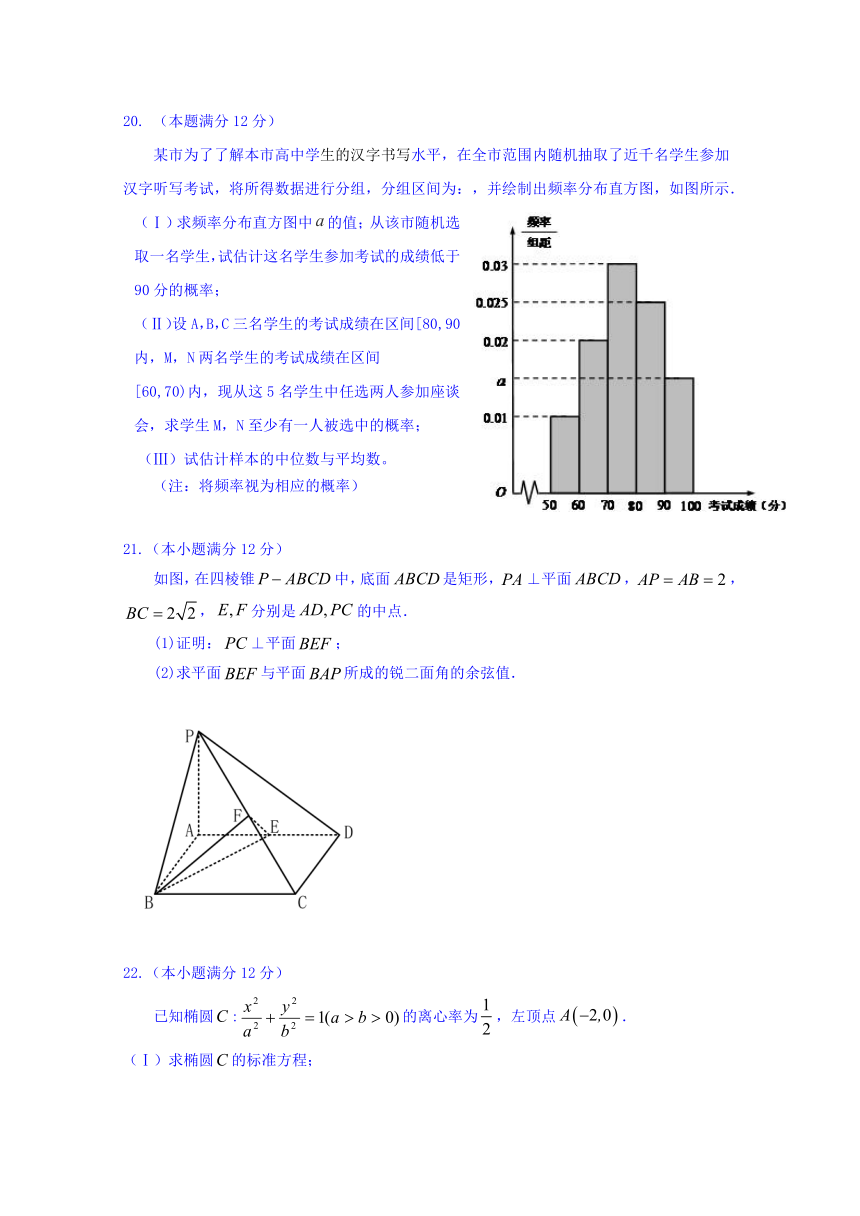
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:,并绘制出频率分布直方图,如图所示.
(Ⅰ)求频率分布直方图中的值;从该市随机选取一名学生,试估计这名学生参加考试的成绩低于90分的概率;
(Ⅱ)设A,B,C三名学生的考试成绩在区间[80,90)内,M,N两名学生的考试成绩在区间
[60,70)内,现从这5名学生中任选两人参加座谈会,求学生M,N至少有一人被选中的概率;
(Ⅲ)试估计样本的中位数与平均数。
(注:将频率视为相应的概率)
21.(本小题满分12分)
如图,在四棱锥中,底面是矩形,⊥平面,,,分别是的中点.
(1)证明:⊥平面;
(2)求平面与平面所成的锐二面角的余弦值.
22.(本小题满分12分)
已知椭圆:的离心率为,左顶点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线:与椭圆交于不同两点,且满足.求证:直线恒过定点,并求出定点的坐标;
(Ⅲ)在(Ⅱ)的条件下,过作,垂足为,求的轨迹方程.
成都龙泉中学2016~2017学年度下学期入学考试
高二数学(理科)试卷参考答案
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1—6
ACCDBA
7—12
BBDBCC
二、填空题(本大题共4小题,每小题5分,满分20分.)
13.12
14.
解析:,当且仅当时取等号。
所以的最小值为3.
15.
16.②③④
三、解答题(本部分共计6小题,满分70分.解答应写出文字说明,证明过程或演算步骤,请在指定区域内作答,否则该题计为零分.)17.解:(1)因为,又,
所以
………2分
由正弦定理,得
…………5分
(2)因为,
所以.
所以
…………7分
由余弦定理,得.
所以
…………10分
18.解析:(1)证明:
于是
……4分
即数列是以为公比的等比数列.
因为,所以
……6分
(2)
①
②
……8分
①②得
……10分
故
……12分
19.解:椭圆的焦点为,离心率为,…………2分
故双曲线的焦点为,离心率为4,…………4分
设双曲线,则,,所以,
故双曲线:,…………8分
其渐进线方程为:或.…………12分
20.
解(I)估计这名学生参加考试的成绩低于90分的概率为0.85
(Ⅱ)从这5名学生代表中任选两人的所有选法共有10种,分别为:AB,AC,AM,AN,BC,BM,BN,CM,CN,MN,代表M,N至少有一人被选中的选法共7种,分别为:AM,AN,BM,BN,CM,CN,MN
设”学生代表M,N至少一人被选中”为事件D,P(D)=
∴学生代表M,N至少一人被选中的概率为
(Ⅲ)样本的中位数为,平均数为76.5.
21.(1)法一:∵,且为的中点,
∴⊥………3分
连结,∵,且为的中点,
∴⊥
∴⊥平面……………………………6分
法二:证明:如图,以A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系.
∵AP=AB=2,BC=AD=2,四边形ABCD是矩形,
∴A,B,C,D,P的坐标为A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
又E,
F分别是AD,PC的中点,∴E(0,,0),F(1,,1).……………………2分
∴=(2,2,-2),=(-1,,1),=(1,0,1).
∴·=-2+4-2=0,·=2+0-2=0.
………………………………………4分
∴⊥,⊥
∴PC⊥BF,PC⊥EF.又BF∩EF=F,
∴PC⊥平面BEF.
……………………………………………………………………………6分
(2)解:由(1)知平面BEF的一个法向量==(2,2,-2),………………………9分
平面BAP的一个法向量==(0,2,0),∴.
设平面BEF与平面BAP的夹角为θ,
则====,
∴平面与平面所成的锐二面角的余弦值为.……………………………12分
22.解:(Ⅰ)设椭圆的半焦距为,由题意知
因此椭圆的标准方程为.…………3分
(Ⅱ)由(Ⅰ)知,,设
把,代入得:,………4分
,
…………5分
若,则
…………8分
,,直线:,即直线恒过定点.…………9分
(Ⅲ)设,由(Ⅱ)知直线恒过定点,,,所以
的轨迹是以为直径的圆(除点外),则的轨迹方程为.
…………12分
PAGE
高二数学(理科)试卷
本试卷分第I卷(选择题)和第II卷,共4页,满分150分,考试时间120分钟.
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题纸上.
2.考生作答时,请将答案答在答题纸上,在本试卷上答题无效.按照题号在各题的答题区域内作答,超出答题区域书写的答案无效.
3.答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚(选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号).
4.保持答题纸纸面清洁,不破损.考试结束后,将本试卷自行保存,答题纸交回.
第I卷(选择题
共60分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若集合,且,则集合B可能是
A.
B.
C.
D.R
2.已知命题p: x0∈,x+1<0,则
A. p: x∈,x2+1>0
B. p: x∈,x2+1>0
C. p: x∈,x2+1≥0
D. p: x∈,x2+1≥0
3.点在边长为1的正方形内运动,则动点到顶点的距离的概率为
A.
B.
C.
D.
4.设数列的通项公式,其前项和为,则
A.
B.
C.
D.
5.
已知一个几何体的三视图如图所示,则该几何体的体积为
B.
C.
D.2
6.
已知,若,则
A.
B.
C.
D.
7.
已知分别为双曲线的左、右顶点,
是上一点,且直线的斜率之积为,则的离心率为
A.
B.
C.
D.
8.
已知程序框图如图所示,则该程序框图的功能是
A.求数列的前10项和
B.求数列的前10项和
C.求数列的前11项和
D.求数列的前11项和
9.设球的半径为时间t的函数,若球的体积以均匀速度c增长,则球的表面积的增长速度与球半径
A.
成正比,比例系数为C
B.
成正比,比例系数为2C
C.成反比,比例系数为C
D.
成反比,比例系数为2C
10.在四棱锥中,底面是边长为2的菱形,,对角线AC与BD相交于点O,平面,PB与平面所成角为,若E是PB的中点,则异面直线DE与PA所成角的余弦值为
A.
B.
C.
D.
11.
已知定义在上的函数(为实数)为偶函数,记
,则
的大小关系为
A.
B.
C.
D.
12.过抛物线的焦点F作两条相互垂直的射线,分别与抛物线相交于点M,N,过弦MN的中点P作抛物线准线的垂线PQ,垂足为Q,则的最大值为
A.
B.
C.
D.
第Ⅱ卷
非选择题(共90分)
二、填空题(本大题共4小题,每小题5分,满分20分.)
13.
已知向量,若⊥,则
14.
若正数,满足,则的最小值为_________.
15.人造地球卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为,卫星近地点、远地点离地面的距离分别为,则卫星轨道的离心率
.(请用表示)
16.
设分别是双曲线的左、右焦点,A为双曲线的左顶点,以线段为直径的圆O与双曲线的一个交点为P,与轴交于B,D两点,且与双曲线的一条渐近线交于M,N两点,则下列命题正确的是
.(写出所有正确的命题编号)
①线段BD是双曲线的虚轴;②的面积为;
③若,则双曲线C的离心率为;④的内切圆的圆心到轴的距离为.
三、解答题(本部分共计6小题,满分70分.解答应写出文字说明,证明过程或演算步骤,请在指定区域内作答,否则该题计为零分.)
17.(本小题满分10分)
在中,角,,所对的边分别为,,,且,.
(1)若,求的值;
(2)若的面积,求,的值.
18.(本题满分12分)
设数列满足:,.
(1)证明:数列为等比数列,并求出数列的通项公式;
(2)求数列的前项和.
19.(本小题满分12分)
已知双曲线与椭圆共焦点,且它们的离心率之和为,求双曲线的标准方程及其渐进线方程.
20.
(本题满分12分)
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据进行分组,分组区间为:,并绘制出频率分布直方图,如图所示.
(Ⅰ)求频率分布直方图中的值;从该市随机选取一名学生,试估计这名学生参加考试的成绩低于90分的概率;
(Ⅱ)设A,B,C三名学生的考试成绩在区间[80,90)内,M,N两名学生的考试成绩在区间
[60,70)内,现从这5名学生中任选两人参加座谈会,求学生M,N至少有一人被选中的概率;
(Ⅲ)试估计样本的中位数与平均数。
(注:将频率视为相应的概率)
21.(本小题满分12分)
如图,在四棱锥中,底面是矩形,⊥平面,,,分别是的中点.
(1)证明:⊥平面;
(2)求平面与平面所成的锐二面角的余弦值.
22.(本小题满分12分)
已知椭圆:的离心率为,左顶点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线:与椭圆交于不同两点,且满足.求证:直线恒过定点,并求出定点的坐标;
(Ⅲ)在(Ⅱ)的条件下,过作,垂足为,求的轨迹方程.
成都龙泉中学2016~2017学年度下学期入学考试
高二数学(理科)试卷参考答案
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1—6
ACCDBA
7—12
BBDBCC
二、填空题(本大题共4小题,每小题5分,满分20分.)
13.12
14.
解析:,当且仅当时取等号。
所以的最小值为3.
15.
16.②③④
三、解答题(本部分共计6小题,满分70分.解答应写出文字说明,证明过程或演算步骤,请在指定区域内作答,否则该题计为零分.)17.解:(1)因为,又,
所以
………2分
由正弦定理,得
…………5分
(2)因为,
所以.
所以
…………7分
由余弦定理,得.
所以
…………10分
18.解析:(1)证明:
于是
……4分
即数列是以为公比的等比数列.
因为,所以
……6分
(2)
①
②
……8分
①②得
……10分
故
……12分
19.解:椭圆的焦点为,离心率为,…………2分
故双曲线的焦点为,离心率为4,…………4分
设双曲线,则,,所以,
故双曲线:,…………8分
其渐进线方程为:或.…………12分
20.
解(I)估计这名学生参加考试的成绩低于90分的概率为0.85
(Ⅱ)从这5名学生代表中任选两人的所有选法共有10种,分别为:AB,AC,AM,AN,BC,BM,BN,CM,CN,MN,代表M,N至少有一人被选中的选法共7种,分别为:AM,AN,BM,BN,CM,CN,MN
设”学生代表M,N至少一人被选中”为事件D,P(D)=
∴学生代表M,N至少一人被选中的概率为
(Ⅲ)样本的中位数为,平均数为76.5.
21.(1)法一:∵,且为的中点,
∴⊥………3分
连结,∵,且为的中点,
∴⊥
∴⊥平面……………………………6分
法二:证明:如图,以A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系.
∵AP=AB=2,BC=AD=2,四边形ABCD是矩形,
∴A,B,C,D,P的坐标为A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
又E,
F分别是AD,PC的中点,∴E(0,,0),F(1,,1).……………………2分
∴=(2,2,-2),=(-1,,1),=(1,0,1).
∴·=-2+4-2=0,·=2+0-2=0.
………………………………………4分
∴⊥,⊥
∴PC⊥BF,PC⊥EF.又BF∩EF=F,
∴PC⊥平面BEF.
……………………………………………………………………………6分
(2)解:由(1)知平面BEF的一个法向量==(2,2,-2),………………………9分
平面BAP的一个法向量==(0,2,0),∴.
设平面BEF与平面BAP的夹角为θ,
则====,
∴平面与平面所成的锐二面角的余弦值为.……………………………12分
22.解:(Ⅰ)设椭圆的半焦距为,由题意知
因此椭圆的标准方程为.…………3分
(Ⅱ)由(Ⅰ)知,,设
把,代入得:,………4分
,
…………5分
若,则
…………8分
,,直线:,即直线恒过定点.…………9分
(Ⅲ)设,由(Ⅱ)知直线恒过定点,,,所以
的轨迹是以为直径的圆(除点外),则的轨迹方程为.
…………12分
PAGE
同课章节目录
