第4章相交线与平行线单元检测B卷
图片预览


文档简介
湘教版七年级下第4章相交线与平行线单元检测B卷
姓名:__________班级:__________考号:__________
、选择题(本大题共12小题的)
1.正多边形的一个内角是150°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
2.下列说法正确的是( )
A.若两条直线被第三条直线所截,则同旁内角互补
B.相等的角是对顶角
C.有一条公共边并且和为180°的两个角互为邻补角
D.若三条直线两两相交,则共有6对对顶角
3.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
A.20° B.25° C.30° D.40°
4.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B. 35° C. 36° D.40°
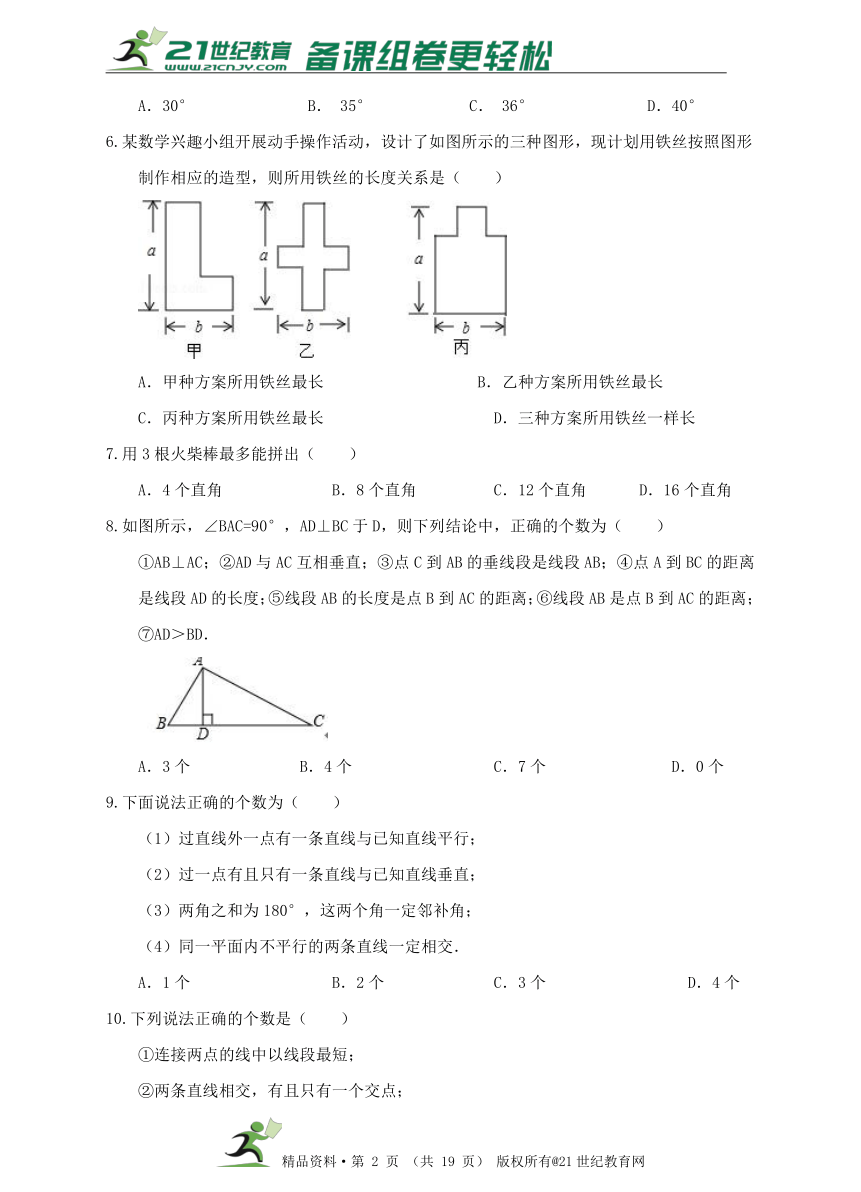
6.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
7.用3根火柴棒最多能拼出( )
A.4个直角 B.8个直角 C.12个直角 D.16个直角
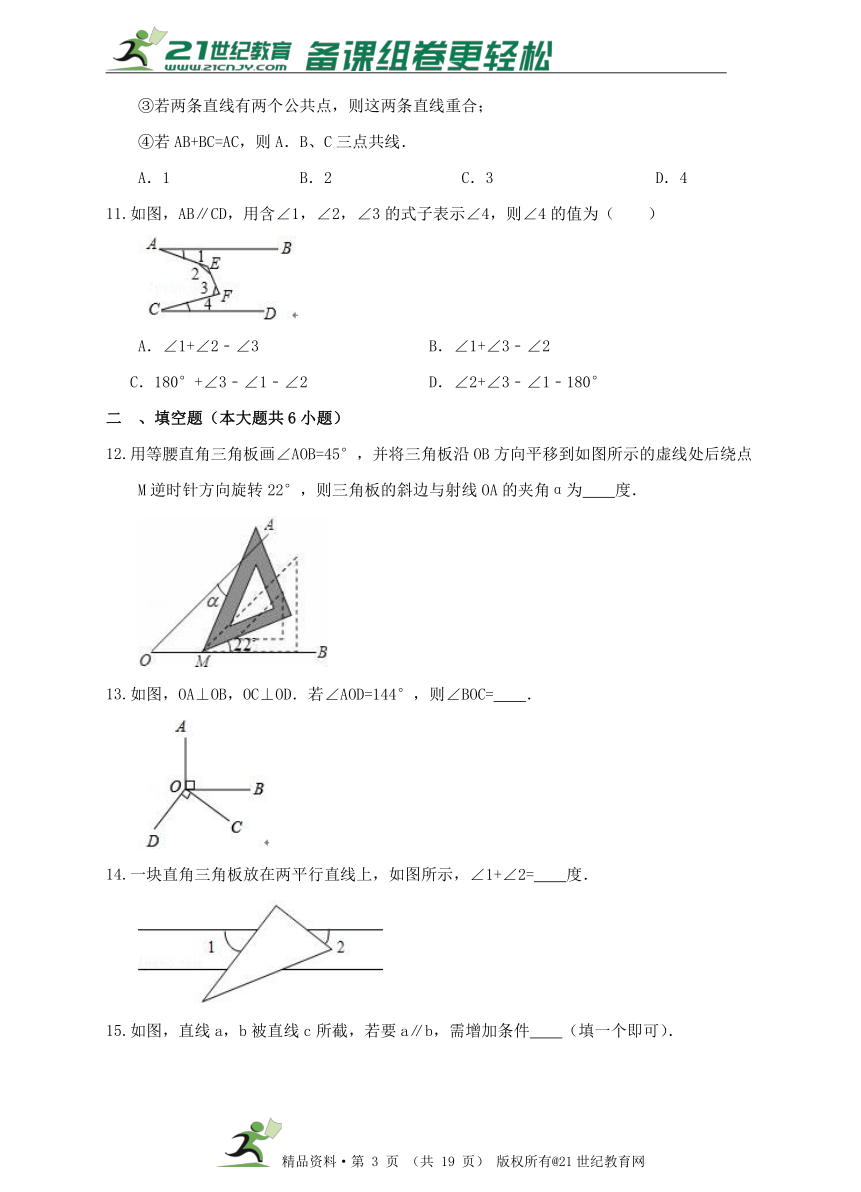
8.如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( )
①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离;⑦AD>BD.
A.3个 B.4个 C.7个 D.0个
9.下面说法正确的个数为( )
(1)过直线外一点有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)两角之和为180°,这两个角一定邻补角;
(4)同一平面内不平行的两条直线一定相交.
A.1个 B.2个 C.3个 D.4个
10.下列说法正确的个数是( )
①连接两点的线中以线段最短;
②两条直线相交,有且只有一个交点;
③若两条直线有两个公共点,则这两条直线重合;
④若AB+BC=AC,则A.B、C三点共线.
A.1 B.2 C.3 D.4
11.如图,AB∥CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( )
A.∠1+∠2﹣∠3 B.∠1+∠3﹣∠2
C.180°+∠3﹣∠1﹣∠2 D.∠2+∠3﹣∠1﹣180°
、填空题(本大题共6小题)
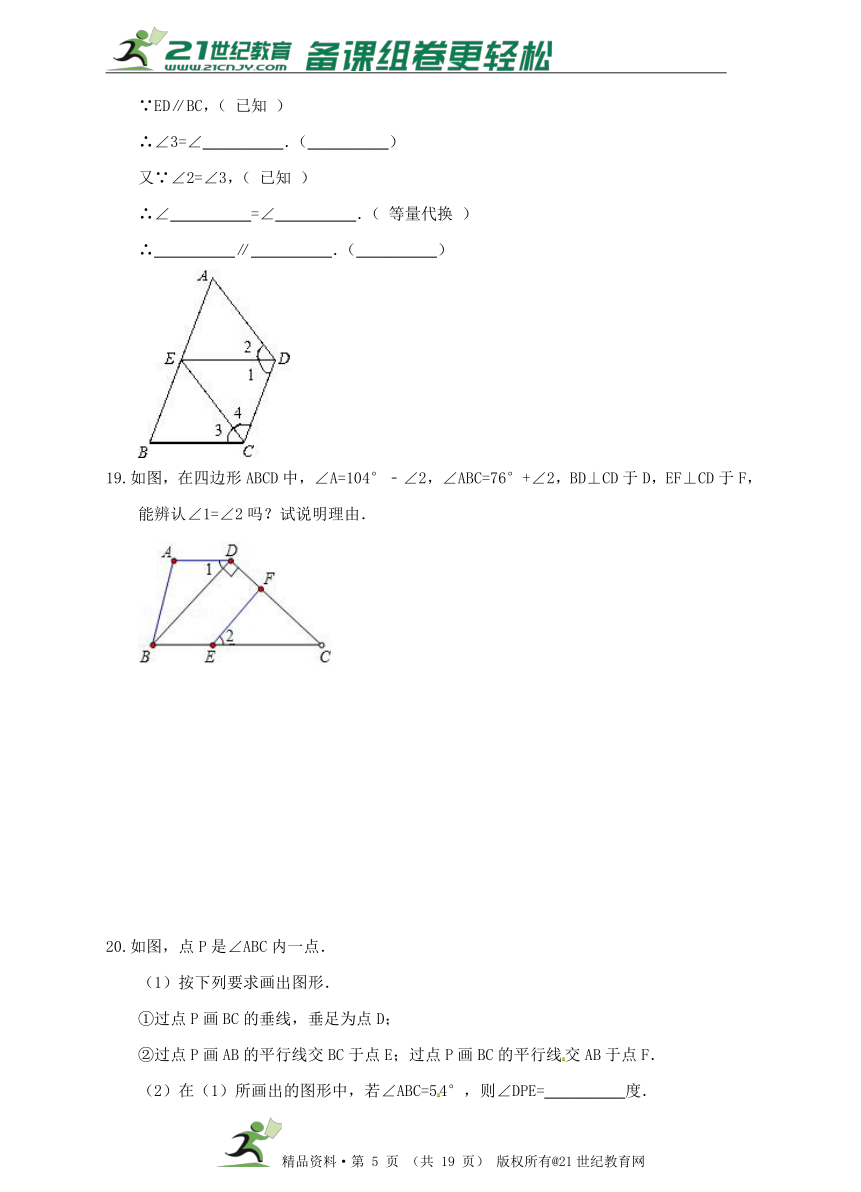
12.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为 度.
13.如图,OA⊥OB,OC⊥OD.若∠AOD=144°,则∠BOC= .
14.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 度.
15.如图,直线a,b被直线c所截,若要a∥b,需增加条件 (填一个即可).
16.如图,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为 度(用关于α的代数式表示).
17.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°.∠BCD=n°,则∠BED的度数为 度.
、解答题(本大题共8小题)
18.如图,AB∥DC,∠1=∠B,∠2=∠3.
(1)ED与BC平行吗?请说明理由;
(2)AD与EC的位置关系如何?为什么?
(3)若∠A=48°,求∠4的度数.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 )
∴∠1=∠__________.(__________)
又∵∠1=∠B,( 已知 )
∴∠B=__________,( 等量代换 )
∴__________∥__________.(__________)
(2)AD与EC的位置关系是:__________.
∵ED∥BC,( 已知 )
∴∠3=∠__________.(__________)
又∵∠2=∠3,( 已知 )
∴∠__________=∠__________.( 等量代换 )
∴__________∥__________.(__________)
19.如图,在四边形ABCD中,∠A=104°﹣∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.
20.如图,点P是∠ABC内一点.
(1)按下列要求画出图形.
①过点P画BC的垂线,垂足为点D;
②过点P画AB的平行线交BC于点E;过点P画BC的平行线交AB于点F.
(2)在(1)所画出的图形中,若∠ABC=54°,则∠DPE=__________度.
21.如图所示,AB∥CD,∠CFE的平分线与∠EGB平分线的反向延长线交于点P,若∠E=20°,则∠FPH的度数为多少?
22.如图,AB∥CD,直线EF分别与AB、CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°.
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)求∠HNG
23.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
24.如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
25.如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A.∠C有怎样的关系?证明你的结论.
(2)当点P移动到AB的外侧时,如图(2),是否仍有(1)的结论?如果不是 ,请写出你的猜想(不要求证明).
(3)当点P移动到如图(3)的位置时,∠P与∠A.∠C又有怎样的关系?能否利用(1)的结论来证明?还有其他的方法吗?请写出一种.
湘教版七年级下第4章相交线与平行线单元检测B卷答案解析
、选择题
1.分析: 一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.
解:外角是:180°﹣150°=30°,
360°÷30°=12.
则这个正多边形是正十二边形.
故选:C.
2. 分析: 根据平行线的性质、对顶角的定义和性质、邻补角的定义判断.
解:A.应该是“若两条平行直线被第三条直线所截,则同旁内角互补”,故错误;
B、相等的角不一定都是对顶角,如两直线平行,其中的同位角相等但不是对顶角,故错误;
C、如果这两个角在公共边的同侧,则不是邻补角,故错误;
D、正确.
故选D.
3. 分析: 根据题意可得AH平分∠CAB,再根据平行线的性质可得∠CAB的度数,再根据角平分线的性质可得答案.
解:由题意可得:AH平分∠CAB,
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=140°,
∴∠CAB=40°,
∵AH平分∠CAB,
∴∠HAB=20°,
∴∠AHC=20°.
故选A.
4. 分析: 根据垂线段的定义直接观察图形进行判断.
解:从左向右第一个图形中,BE不是线段,故错误;
第二个图形中,BE不垂直AC,所以错误;
第三个图形中,是过点E作的AC的垂线,所以错误;
第四个图形中,过点C作的BE的垂线,也错误.
故选D.
5. 分析: 过点A作l1的平行线,过点B作l2的平行线,根据两直线平行,内错角相等可得∠3=∠1,∠4=∠2,再根据两直线平行,同旁内角互补求出∠CAB+∠ABD=180°,然后计算即可得解
解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选A.
6. 分析: 分别利用平移的性质得出各图形中所用铁丝的长度,进而得出答案.
解:由图形可得出:甲所用铁丝的长度为:2a+2b,
乙所用铁丝的长度为:2a+2b,
丙所用铁丝的长度为:2a+2b,
故三种方案所用铁丝一样长.
故选:D.
7. 分析: 当3根火柴棒有公共交点且两两垂直时,可拼出“三线十二角”,十二个角都是直角.
解:如图所示,当3根火柴棒有公共交点且两两垂直时(是立体图形),
可构成12个直角.
故选C.
8. 分析: 本题要根据垂线定义、垂线段定义(定理)、点到直线的距离定义,逐一判断.
解:∵∠BAC=90°∴①AB⊥AC正确;
∵∠DAC≠90°,∴AD与AC不互相垂直,所以②错误;
点C到AB的垂线段应是线段AC,所以③错误;
点A到BC的距离是线段AD的长度,所以④正确;
根据“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.”可知⑤正确;
线段AB的长度是点B到AC的距离,所以⑥错误;
AD>BD不一定,所以⑦错误.
故选A.
9. 分析: 根据同一平面内,过直线外一点有一条直线和已知直线平行即可判断(1);在同一平面内,过一点有且只有一条直线和已知直线垂直即可判断(2);举出反例即可判断(3);根据在同一平面内,两直线的位置关系是平行或相交,即可判断(4).
解:过直线外一点有一条直线和已知直线平行,故(1)正确;
只有在同一平面内,过一点有且只有一条直线和已知直线垂直,故(2)错误;
如图:
∠ABC=∠DEF=90°,且∠ABC+∠DEF=180°,但是两角不是邻补角,故(3)错误;
同一平面内不平行的两条直线一定相交正确,
因为不特别指出时,一般认为,两条直线重合就是同一条直线,所以所提出的命题是正确的,故(4)正确.
即正确的个数是2个.
故选B.
10. 分析: ①根据线段的基本性质解答;②、③由直线的定义解答;④根据两点间的距离解答.
解:①线段的基本性质是:所有连接两点的线中,线段最短.故本选项正确;
②任意两个点可以通过一条直线连接,所以,两条直线相交,有且只有一个交点,故本选项正确;
③任意两个点可以通过一条直线连接,若两条直线有两个公共点,则这两条直线重合;故本选项正确;
④根据两点间的距离知,故本选项正确;
综上所述,以上说法正确的是①②③④共4个.
故选D.
11. 分析: 先过点E作EG∥AB,过点F作FH∥CD,利用平行线的性质求得∠GEF和∠EFH,最后根据∠CFH=∠3﹣∠EFH,求得∠4即可.
解:过点E作EG∥AB,过点F作FH∥CD,
∵AB∥CD,
∴AB∥CD∥EG∥FH,
∴∠1=∠AEG,
∴∠GEF=∠2﹣∠1,
∵EG∥FH,
∴∠EFH=180°﹣∠GEF=180°﹣(∠2﹣∠1)=180°﹣∠2+∠1,
∴∠CFH=∠3﹣∠EFH=∠3﹣(180°﹣∠2+∠1)=∠3+∠2﹣∠2﹣180°,
∵FH∥CD,
∴∠4=∠3+∠2﹣∠1﹣180°,
故选(D)
、填空题
12. 分析: 由平移的性质知,AO∥SM,再由平行线的性质可得∠WMS=∠OWM,即可得答案.
解:由平移的性质知,AO∥SM,
故∠WMS=∠OWM=22°;
故答案为:22.
13. 分析: 根据垂直的定义知∠AOB=∠COD=90°,然后由周角的定义即可求得∠BOC的度数.
解:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°;
又∵∠AOD+∠AOB+∠BOC+∠COD=360°,∠AOD=144°,
∴∠BOC=36°;
故答案是:36°.
14. 分析: 根据对顶角相等得到∠1=∠3,∠2=∠4,而三角形尺为直尺,即可得到∠1+∠2=90°.
解:如图,
∵∠1=∠3,∠2=∠4,
而∠3+∠4=90°,
∴∠1+∠2=90°.
故答案为:90.
15. 分析: 欲证a∥b,在图中发现a、b被一直线c所截,故可按同位角相等两直线平行补充条件.
解:∵∠1=∠3,
∴a∥b(同位角相等,两直线平行).
故答案为:∠1=∠3
16.分析: 根据∠ECA=α,∠ECA+∠ECB=180°可得:∠ECB=180°-α,根据CD平分∠ECB可得∠DCB=∠ECB=90°-α,根据FG∥CD可得:∠GFB=∠DCB=90°-α.
17. 分析: 先根据角平分线的定义,得出∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,再根据三角形内角和定理,推理得出∠BAD+∠BCD=2∠E,进而求得∠E的度数.
解:∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,
∵∠ABE+∠BAD=∠E+∠ADE,∠BCD+∠CDE=∠E+∠CBE,
∴∠ABE+∠BAD+∠BCD+∠CDE=∠E+∠ADE+∠E+∠CBE,
∴∠BAD+∠BCD=2∠E,
∵∠BAD=70°,∠BCD=n°,
∴∠E=(∠D+∠B)=35+.
故答案为:35+
、解答题
18. 分析: 只需要根据两直线平行的判定方法及性质填写对应的空即可
解:(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 ),
∴∠1=∠AED( 两直线平行,内错角相等 ),
又∵∠1=∠B( 已知 ),
∴∠B=∠AED( 等量代换 ),
∴ED∥BC( 同位角相等,两直线平行 ),
故答案为:AED,两直线平行,内错角相等,∠AED,ED,BC;
(2)AD与EC的位置关系是:AD∥EC,
∵ED∥BC( 已知 ),
∴∠3=∠CED( 两直线平行,内错角相等 ),
又∵∠2=∠3( 已知 ),
∴∠2=∠CED( 等量代换 ),
∴AD∥EC( 内错角相等,两直线平行 ),
故答案为:AD∥EC,CED,两直线平行,内错角相等,2,CED,AD,EC,内错角相等,两直线平行.
19. 分析: 根据同旁内角互补,两直线平行先求出AD∥BC,然后根据两直线平行,内错角相等求出∠1=∠DBC,再根据垂直于同一直线的两直线互相平行求出BD∥EF,然后根据两直线平行,同位角相等即可得解.
解:能辨认∠1=∠2.
理由如下:∵∠A=104°﹣∠2,∠ABC=76°+∠2,
∴∠A+∠ABC=104°﹣∠2+76°+∠2=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠DBC(两直线平行,内错角相等),
∵BD⊥DC,EF⊥DC,
∴BD∥EF(根据垂直于同一直线的两直线平行),
∴∠2=∠DBC(两直线平行,同位角相等),
∴∠1=∠2.
20. 分析: (1)①直接利用尺规过点P作PD⊥BC的垂线即可;
②利用尺规通过平移分别作BC,AB的平行线即可;
(2)首先得到四边形FBEP是平行四边形,然后利用平行四边形的性质得到∠EPF=∠B,然后利用垂直的定义求得结论即可.
解:(1)如图所示;
(2)∵AB∥PE,FP∥BD,
∴四边形FBPE是平行四边形,
∴∠FPE=∠B=54°,
∴∠DPE=90°﹣54°=36°,
故答案为:36.
21. 分析: 作PM∥CD,如图,则AB∥PM∥CD,根据平行线的性质得∠4=∠2,∠3=∠1,则∠FPH=∠1+∠2,再利用角平分线定义得到∠CFQ=2∠1,∠EGB=2∠BGH,而∠BGH=∠2,所以∠FPH=(∠CFQ+∠EGB),利用三角形外角性质得∠EGB=∠E+∠EQG,利用邻补角得∠EQG=180°﹣∠EQA,利用平行线的性质得∠CFQ=∠EQA,则∠EGB=∠E+180°﹣∠CFQ,于是得到∠FPH=(∠CFQ+∠E+180°﹣∠CFQ)=(20°+180°),然后把∠E=20°代入计算即可.
解:作PM∥CD,如图,
∵AB∥CD,
∴AB∥PM∥CD,
∴∠4=∠2,∠3=∠1,
∴∠FPH=∠1+∠2,
∵∠CFE的平分线与∠EGB的平分线的反向延长线交于点P,
∴∠CFQ=2∠1,∠EGB=2∠BGH,
∵∠BGH=∠2,
∴∠FPH=(∠CFQ+∠EGB),
∵∠EGB=∠E+∠EQG,
∵∠EQG=180°﹣∠EQA,
∵CD∥AB,
∴∠CFQ=∠EQA,
∴∠EGB=∠E+180°﹣∠CFQ,
∴∠FPH=(∠CFQ+∠E+180°﹣∠CFQ)
=(20°+180°)
=100°.
22. 分析: (1)根据平行线的性由AB∥CD得到∠EHD=∠1=50°,再根据对顶角相等可得到∠2的度数;
(2)根据垂直的定义得到∠MGH=90°,∠NHF=90°,然后根据平行线的判定有HN∥GM;
(3)先由HN⊥EF得到∠NHG=90°,再根据对顶角相等得∠NGH=∠1=50°,然后根据互余可计算出∠HNG=40°.
解:(1)∵AB∥CD,
∴∠EHD=∠1=50°,
∴∠2=∠EHD=50°;
(2)∵GM⊥EF,HN⊥EF,
∴∠MGH=90°,∠NHF=90°,
∴∠MGH=∠NHF,
∴HN∥GM;
(3)∵HN⊥EF,
∴∠NHG=90°
∵∠NGH=∠1=50°,
∴∠HNG=90°﹣50°=40°.
故答案为40.
23. 分析: (1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;
(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.
解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
24. 分析: (1)根据四边形的内角和,可得∠ABC+∠ADC=180°,然后,根据角平分线的性质,即可得出;
(2)由互余可得∠1=∠DFC,根据平行线的判定,即可得出.
解:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
25. 分析: (1)延长AP后通过外角定理可得出结论.
(2)利用外角定理可直接得出答案.
(3)延长BA到E,延长DC到F,利用内角和定理解答.
证明:(1)∠P=∠A+∠C,
延长AP交CD与点E.
∵AB∥CD,∴∠A=∠AEC.
又∵∠APC是△PCE的外角,
∴∠APC=∠C+∠AEC.
∴∠APC=∠A+∠C.
(2)否;∠P=∠C﹣∠A.
(3)∠P=360°﹣(∠A+∠C).
①延长BA到E,延长DC到F,
由(1)得∠P=∠PAE+∠PCF.
∵∠PAE=180°﹣∠PAB,∠PCF=180°﹣∠PCD,
∴∠P=360°﹣(∠PAB+∠PCD).
②连接AC.
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵∠PAC+∠PCA=180°﹣∠P,
∴∠CAB+∠ACD+∠PAC+∠PCA=360°﹣∠P,
即∠P=360°﹣(∠PAB+∠PCD).
姓名:__________班级:__________考号:__________
、选择题(本大题共12小题的)
1.正多边形的一个内角是150°,则这个正多边形的边数为( )
A.10 B.11 C.12 D.13
2.下列说法正确的是( )
A.若两条直线被第三条直线所截,则同旁内角互补
B.相等的角是对顶角
C.有一条公共边并且和为180°的两个角互为邻补角
D.若三条直线两两相交,则共有6对对顶角
3.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
A.20° B.25° C.30° D.40°
4.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B. 35° C. 36° D.40°
6.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
7.用3根火柴棒最多能拼出( )
A.4个直角 B.8个直角 C.12个直角 D.16个直角
8.如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( )
①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离;⑦AD>BD.
A.3个 B.4个 C.7个 D.0个
9.下面说法正确的个数为( )
(1)过直线外一点有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)两角之和为180°,这两个角一定邻补角;
(4)同一平面内不平行的两条直线一定相交.
A.1个 B.2个 C.3个 D.4个
10.下列说法正确的个数是( )
①连接两点的线中以线段最短;
②两条直线相交,有且只有一个交点;
③若两条直线有两个公共点,则这两条直线重合;
④若AB+BC=AC,则A.B、C三点共线.
A.1 B.2 C.3 D.4
11.如图,AB∥CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( )
A.∠1+∠2﹣∠3 B.∠1+∠3﹣∠2
C.180°+∠3﹣∠1﹣∠2 D.∠2+∠3﹣∠1﹣180°
、填空题(本大题共6小题)
12.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为 度.
13.如图,OA⊥OB,OC⊥OD.若∠AOD=144°,则∠BOC= .
14.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 度.
15.如图,直线a,b被直线c所截,若要a∥b,需增加条件 (填一个即可).
16.如图,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为 度(用关于α的代数式表示).
17.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°.∠BCD=n°,则∠BED的度数为 度.
、解答题(本大题共8小题)
18.如图,AB∥DC,∠1=∠B,∠2=∠3.
(1)ED与BC平行吗?请说明理由;
(2)AD与EC的位置关系如何?为什么?
(3)若∠A=48°,求∠4的度数.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 )
∴∠1=∠__________.(__________)
又∵∠1=∠B,( 已知 )
∴∠B=__________,( 等量代换 )
∴__________∥__________.(__________)
(2)AD与EC的位置关系是:__________.
∵ED∥BC,( 已知 )
∴∠3=∠__________.(__________)
又∵∠2=∠3,( 已知 )
∴∠__________=∠__________.( 等量代换 )
∴__________∥__________.(__________)
19.如图,在四边形ABCD中,∠A=104°﹣∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.
20.如图,点P是∠ABC内一点.
(1)按下列要求画出图形.
①过点P画BC的垂线,垂足为点D;
②过点P画AB的平行线交BC于点E;过点P画BC的平行线交AB于点F.
(2)在(1)所画出的图形中,若∠ABC=54°,则∠DPE=__________度.
21.如图所示,AB∥CD,∠CFE的平分线与∠EGB平分线的反向延长线交于点P,若∠E=20°,则∠FPH的度数为多少?
22.如图,AB∥CD,直线EF分别与AB、CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°.
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)求∠HNG
23.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
24.如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
25.如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A.∠C有怎样的关系?证明你的结论.
(2)当点P移动到AB的外侧时,如图(2),是否仍有(1)的结论?如果不是 ,请写出你的猜想(不要求证明).
(3)当点P移动到如图(3)的位置时,∠P与∠A.∠C又有怎样的关系?能否利用(1)的结论来证明?还有其他的方法吗?请写出一种.
湘教版七年级下第4章相交线与平行线单元检测B卷答案解析
、选择题
1.分析: 一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.
解:外角是:180°﹣150°=30°,
360°÷30°=12.
则这个正多边形是正十二边形.
故选:C.
2. 分析: 根据平行线的性质、对顶角的定义和性质、邻补角的定义判断.
解:A.应该是“若两条平行直线被第三条直线所截,则同旁内角互补”,故错误;
B、相等的角不一定都是对顶角,如两直线平行,其中的同位角相等但不是对顶角,故错误;
C、如果这两个角在公共边的同侧,则不是邻补角,故错误;
D、正确.
故选D.
3. 分析: 根据题意可得AH平分∠CAB,再根据平行线的性质可得∠CAB的度数,再根据角平分线的性质可得答案.
解:由题意可得:AH平分∠CAB,
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=140°,
∴∠CAB=40°,
∵AH平分∠CAB,
∴∠HAB=20°,
∴∠AHC=20°.
故选A.
4. 分析: 根据垂线段的定义直接观察图形进行判断.
解:从左向右第一个图形中,BE不是线段,故错误;
第二个图形中,BE不垂直AC,所以错误;
第三个图形中,是过点E作的AC的垂线,所以错误;
第四个图形中,过点C作的BE的垂线,也错误.
故选D.
5. 分析: 过点A作l1的平行线,过点B作l2的平行线,根据两直线平行,内错角相等可得∠3=∠1,∠4=∠2,再根据两直线平行,同旁内角互补求出∠CAB+∠ABD=180°,然后计算即可得解
解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选A.
6. 分析: 分别利用平移的性质得出各图形中所用铁丝的长度,进而得出答案.
解:由图形可得出:甲所用铁丝的长度为:2a+2b,
乙所用铁丝的长度为:2a+2b,
丙所用铁丝的长度为:2a+2b,
故三种方案所用铁丝一样长.
故选:D.
7. 分析: 当3根火柴棒有公共交点且两两垂直时,可拼出“三线十二角”,十二个角都是直角.
解:如图所示,当3根火柴棒有公共交点且两两垂直时(是立体图形),
可构成12个直角.
故选C.
8. 分析: 本题要根据垂线定义、垂线段定义(定理)、点到直线的距离定义,逐一判断.
解:∵∠BAC=90°∴①AB⊥AC正确;
∵∠DAC≠90°,∴AD与AC不互相垂直,所以②错误;
点C到AB的垂线段应是线段AC,所以③错误;
点A到BC的距离是线段AD的长度,所以④正确;
根据“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.”可知⑤正确;
线段AB的长度是点B到AC的距离,所以⑥错误;
AD>BD不一定,所以⑦错误.
故选A.
9. 分析: 根据同一平面内,过直线外一点有一条直线和已知直线平行即可判断(1);在同一平面内,过一点有且只有一条直线和已知直线垂直即可判断(2);举出反例即可判断(3);根据在同一平面内,两直线的位置关系是平行或相交,即可判断(4).
解:过直线外一点有一条直线和已知直线平行,故(1)正确;
只有在同一平面内,过一点有且只有一条直线和已知直线垂直,故(2)错误;
如图:
∠ABC=∠DEF=90°,且∠ABC+∠DEF=180°,但是两角不是邻补角,故(3)错误;
同一平面内不平行的两条直线一定相交正确,
因为不特别指出时,一般认为,两条直线重合就是同一条直线,所以所提出的命题是正确的,故(4)正确.
即正确的个数是2个.
故选B.
10. 分析: ①根据线段的基本性质解答;②、③由直线的定义解答;④根据两点间的距离解答.
解:①线段的基本性质是:所有连接两点的线中,线段最短.故本选项正确;
②任意两个点可以通过一条直线连接,所以,两条直线相交,有且只有一个交点,故本选项正确;
③任意两个点可以通过一条直线连接,若两条直线有两个公共点,则这两条直线重合;故本选项正确;
④根据两点间的距离知,故本选项正确;
综上所述,以上说法正确的是①②③④共4个.
故选D.
11. 分析: 先过点E作EG∥AB,过点F作FH∥CD,利用平行线的性质求得∠GEF和∠EFH,最后根据∠CFH=∠3﹣∠EFH,求得∠4即可.
解:过点E作EG∥AB,过点F作FH∥CD,
∵AB∥CD,
∴AB∥CD∥EG∥FH,
∴∠1=∠AEG,
∴∠GEF=∠2﹣∠1,
∵EG∥FH,
∴∠EFH=180°﹣∠GEF=180°﹣(∠2﹣∠1)=180°﹣∠2+∠1,
∴∠CFH=∠3﹣∠EFH=∠3﹣(180°﹣∠2+∠1)=∠3+∠2﹣∠2﹣180°,
∵FH∥CD,
∴∠4=∠3+∠2﹣∠1﹣180°,
故选(D)
、填空题
12. 分析: 由平移的性质知,AO∥SM,再由平行线的性质可得∠WMS=∠OWM,即可得答案.
解:由平移的性质知,AO∥SM,
故∠WMS=∠OWM=22°;
故答案为:22.
13. 分析: 根据垂直的定义知∠AOB=∠COD=90°,然后由周角的定义即可求得∠BOC的度数.
解:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°;
又∵∠AOD+∠AOB+∠BOC+∠COD=360°,∠AOD=144°,
∴∠BOC=36°;
故答案是:36°.
14. 分析: 根据对顶角相等得到∠1=∠3,∠2=∠4,而三角形尺为直尺,即可得到∠1+∠2=90°.
解:如图,
∵∠1=∠3,∠2=∠4,
而∠3+∠4=90°,
∴∠1+∠2=90°.
故答案为:90.
15. 分析: 欲证a∥b,在图中发现a、b被一直线c所截,故可按同位角相等两直线平行补充条件.
解:∵∠1=∠3,
∴a∥b(同位角相等,两直线平行).
故答案为:∠1=∠3
16.分析: 根据∠ECA=α,∠ECA+∠ECB=180°可得:∠ECB=180°-α,根据CD平分∠ECB可得∠DCB=∠ECB=90°-α,根据FG∥CD可得:∠GFB=∠DCB=90°-α.
17. 分析: 先根据角平分线的定义,得出∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,再根据三角形内角和定理,推理得出∠BAD+∠BCD=2∠E,进而求得∠E的度数.
解:∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠CBE=∠ABC,∠ADE=∠CDE=∠ADC,
∵∠ABE+∠BAD=∠E+∠ADE,∠BCD+∠CDE=∠E+∠CBE,
∴∠ABE+∠BAD+∠BCD+∠CDE=∠E+∠ADE+∠E+∠CBE,
∴∠BAD+∠BCD=2∠E,
∵∠BAD=70°,∠BCD=n°,
∴∠E=(∠D+∠B)=35+.
故答案为:35+
、解答题
18. 分析: 只需要根据两直线平行的判定方法及性质填写对应的空即可
解:(1)ED∥BC,理由如下:
∵AB∥DC,( 已知 ),
∴∠1=∠AED( 两直线平行,内错角相等 ),
又∵∠1=∠B( 已知 ),
∴∠B=∠AED( 等量代换 ),
∴ED∥BC( 同位角相等,两直线平行 ),
故答案为:AED,两直线平行,内错角相等,∠AED,ED,BC;
(2)AD与EC的位置关系是:AD∥EC,
∵ED∥BC( 已知 ),
∴∠3=∠CED( 两直线平行,内错角相等 ),
又∵∠2=∠3( 已知 ),
∴∠2=∠CED( 等量代换 ),
∴AD∥EC( 内错角相等,两直线平行 ),
故答案为:AD∥EC,CED,两直线平行,内错角相等,2,CED,AD,EC,内错角相等,两直线平行.
19. 分析: 根据同旁内角互补,两直线平行先求出AD∥BC,然后根据两直线平行,内错角相等求出∠1=∠DBC,再根据垂直于同一直线的两直线互相平行求出BD∥EF,然后根据两直线平行,同位角相等即可得解.
解:能辨认∠1=∠2.
理由如下:∵∠A=104°﹣∠2,∠ABC=76°+∠2,
∴∠A+∠ABC=104°﹣∠2+76°+∠2=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠DBC(两直线平行,内错角相等),
∵BD⊥DC,EF⊥DC,
∴BD∥EF(根据垂直于同一直线的两直线平行),
∴∠2=∠DBC(两直线平行,同位角相等),
∴∠1=∠2.
20. 分析: (1)①直接利用尺规过点P作PD⊥BC的垂线即可;
②利用尺规通过平移分别作BC,AB的平行线即可;
(2)首先得到四边形FBEP是平行四边形,然后利用平行四边形的性质得到∠EPF=∠B,然后利用垂直的定义求得结论即可.
解:(1)如图所示;
(2)∵AB∥PE,FP∥BD,
∴四边形FBPE是平行四边形,
∴∠FPE=∠B=54°,
∴∠DPE=90°﹣54°=36°,
故答案为:36.
21. 分析: 作PM∥CD,如图,则AB∥PM∥CD,根据平行线的性质得∠4=∠2,∠3=∠1,则∠FPH=∠1+∠2,再利用角平分线定义得到∠CFQ=2∠1,∠EGB=2∠BGH,而∠BGH=∠2,所以∠FPH=(∠CFQ+∠EGB),利用三角形外角性质得∠EGB=∠E+∠EQG,利用邻补角得∠EQG=180°﹣∠EQA,利用平行线的性质得∠CFQ=∠EQA,则∠EGB=∠E+180°﹣∠CFQ,于是得到∠FPH=(∠CFQ+∠E+180°﹣∠CFQ)=(20°+180°),然后把∠E=20°代入计算即可.
解:作PM∥CD,如图,
∵AB∥CD,
∴AB∥PM∥CD,
∴∠4=∠2,∠3=∠1,
∴∠FPH=∠1+∠2,
∵∠CFE的平分线与∠EGB的平分线的反向延长线交于点P,
∴∠CFQ=2∠1,∠EGB=2∠BGH,
∵∠BGH=∠2,
∴∠FPH=(∠CFQ+∠EGB),
∵∠EGB=∠E+∠EQG,
∵∠EQG=180°﹣∠EQA,
∵CD∥AB,
∴∠CFQ=∠EQA,
∴∠EGB=∠E+180°﹣∠CFQ,
∴∠FPH=(∠CFQ+∠E+180°﹣∠CFQ)
=(20°+180°)
=100°.
22. 分析: (1)根据平行线的性由AB∥CD得到∠EHD=∠1=50°,再根据对顶角相等可得到∠2的度数;
(2)根据垂直的定义得到∠MGH=90°,∠NHF=90°,然后根据平行线的判定有HN∥GM;
(3)先由HN⊥EF得到∠NHG=90°,再根据对顶角相等得∠NGH=∠1=50°,然后根据互余可计算出∠HNG=40°.
解:(1)∵AB∥CD,
∴∠EHD=∠1=50°,
∴∠2=∠EHD=50°;
(2)∵GM⊥EF,HN⊥EF,
∴∠MGH=90°,∠NHF=90°,
∴∠MGH=∠NHF,
∴HN∥GM;
(3)∵HN⊥EF,
∴∠NHG=90°
∵∠NGH=∠1=50°,
∴∠HNG=90°﹣50°=40°.
故答案为40.
23. 分析: (1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;
(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.
解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
24. 分析: (1)根据四边形的内角和,可得∠ABC+∠ADC=180°,然后,根据角平分线的性质,即可得出;
(2)由互余可得∠1=∠DFC,根据平行线的判定,即可得出.
解:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
25. 分析: (1)延长AP后通过外角定理可得出结论.
(2)利用外角定理可直接得出答案.
(3)延长BA到E,延长DC到F,利用内角和定理解答.
证明:(1)∠P=∠A+∠C,
延长AP交CD与点E.
∵AB∥CD,∴∠A=∠AEC.
又∵∠APC是△PCE的外角,
∴∠APC=∠C+∠AEC.
∴∠APC=∠A+∠C.
(2)否;∠P=∠C﹣∠A.
(3)∠P=360°﹣(∠A+∠C).
①延长BA到E,延长DC到F,
由(1)得∠P=∠PAE+∠PCF.
∵∠PAE=180°﹣∠PAB,∠PCF=180°﹣∠PCD,
∴∠P=360°﹣(∠PAB+∠PCD).
②连接AC.
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵∠PAC+∠PCA=180°﹣∠P,
∴∠CAB+∠ACD+∠PAC+∠PCA=360°﹣∠P,
即∠P=360°﹣(∠PAB+∠PCD).
