2017年安徽省蚌埠市高考数学一模试卷(理科)(解析版)
文档属性
| 名称 | 2017年安徽省蚌埠市高考数学一模试卷(理科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-18 23:56:33 | ||
图片预览



文档简介
2017年安徽省蚌埠市高考数学一模试卷(理科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.已知A={x|2x<1},B={x|y=},则A∩B=( )
A.[﹣2,0)
B.[﹣2,0]
C.(0,+∞)
D.[﹣2,+∞)
2.复数Z在映射f下的象为(1+i)Z,则﹣1+2i的原象为( )
A.
B.
C.
D.
3.若cos()=,则cos2α=( )
A.
B.
C.一
D.
4.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
5.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
6.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
7.已知函数f(x)定义域为R,命题:p:f(x)为奇函数,q:
f(x)dx=0,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
8.已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π.若将函数f(x)的图象向左平移个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
A.f(x)=2sin(x+)
B.f(x)=2sin(x+)
C.f(x)=2sin(2x+)
D.f(x)=2sin(2x+)
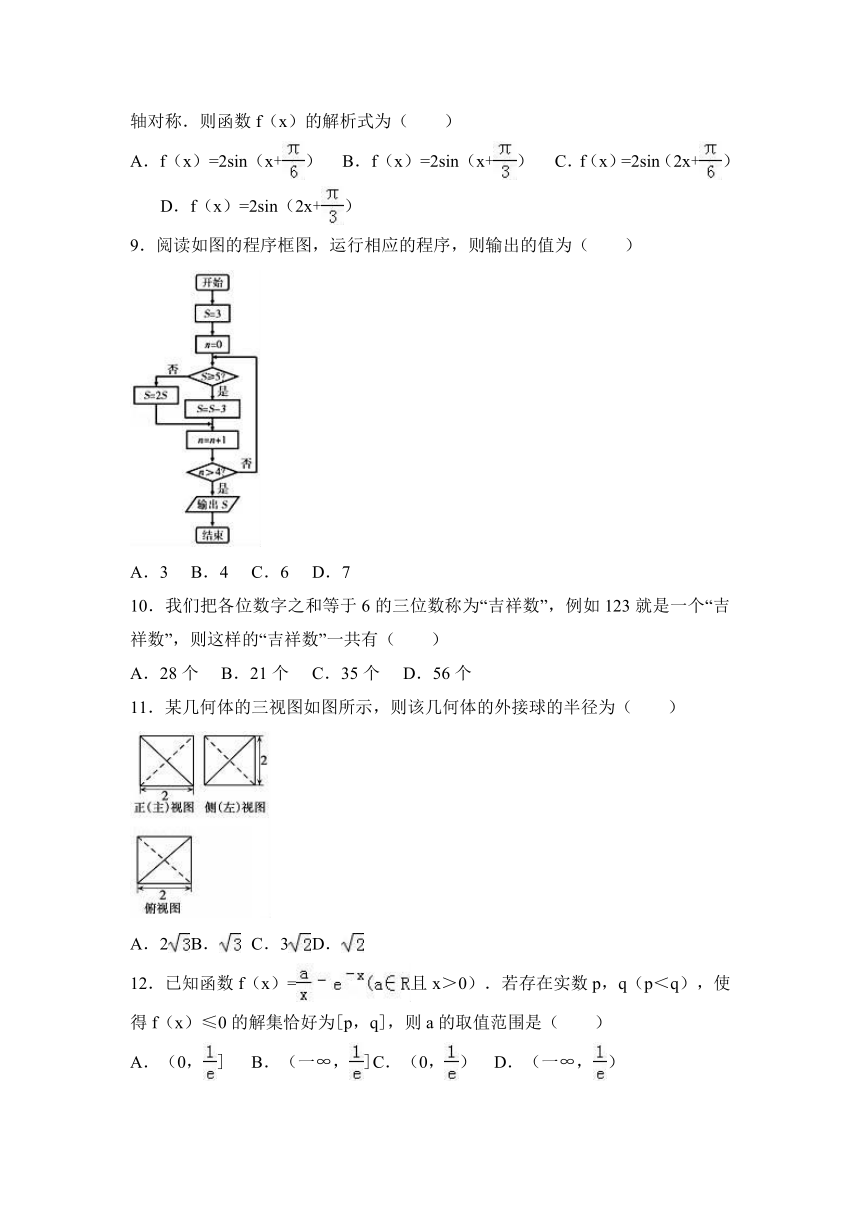
9.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
10.我们把各位数字之和等于6的三位数称为“吉祥数”,例如123就是一个“吉祥数”,则这样的“吉祥数”一共有( )
A.28个
B.21个
C.35个
D.56个
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
12.已知函数f(x)=且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
A.(0,]
B.(一∞,]
C.(0,)
D.(一∞,)
二、填空题:本大题共4小题,每小题5分,共20分,请将答案填在答题卷相应横线上.
13.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
14.若()a的展开式中只有第5项的二项式系数最大,则展开式中常数项是 .
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 斛.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,外接圆半径为1,且=,则△ABC面积的最大值为 .
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.等差数列{an}前n项和为Sn,且S5=45,S6=60.
(1)求{an}的通项公式an;
(2)若数列{an}满足bn+1﹣bn=an(n∈N
)且b1=3,求{}的前n项和Tn.
18.某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
(
I)求高一学生读课外书的人均本数;
(Ⅱ)从高一学生中任意选两名学生,求他们读课外书的本数恰好相等的概率;
(Ⅲ)从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,求随机变量ζ的分布列及数学期望E.
19.在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=,A1F=,CE⊥EF,M为AB中点
(
I)证明:EF⊥平面CME;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
20.已知椭圆C:
+=1(a>b>0)的长轴长为4,离心率为,右焦点为F.
(1)求椭圆C的方程;
(2)直线l与椭圆C相切于点P(不为椭圆C的左、右顶点),直线l与直线x=2交于点A,直线l与直线x=﹣2交于点B,请问∠AFB是否为定值?若不是,请说明理由;若是,请证明.
21.已知函数f(x)=(其中e是自然对数的底数,a∈R).
(
I)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(Ⅱ)若函数f(x)在区间(0,1]上是单调函数,求a的最大值.
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
2017年安徽省蚌埠市高考数学一模试卷(理科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.已知A={x|2x<1},B={x|y=},则A∩B=( )
A.[﹣2,0)
B.[﹣2,0]
C.(0,+∞)
D.[﹣2,+∞)
【考点】交集及其运算.
【分析】求出集合A,B,根据集合的基本运算,即可得到结论.
【解答】解:A={x|2x<1}={x|x<0}=(﹣∞,0),
B={x|y=}=[﹣2,+∞)
∴A∩B=[﹣2,0),
故选:A.
2.复数Z在映射f下的象为(1+i)Z,则﹣1+2i的原象为( )
A.
B.
C.
D.
【考点】复数代数形式的乘除运算;映射.
【分析】先由已知,得出﹣1+2i的原象为,再化简计算即可.
【解答】解:根据题意,若设﹣1+2i的原象为复数z,则得出(1+i)z=﹣1+2i,
所以z===
故选B
3.若cos()=,则cos2α=( )
A.
B.
C.一
D.
【考点】二倍角的余弦.
【分析】由已知利用诱导公式可求sinα的值,进而利用二倍角的余弦函数公式即可计算得解.
【解答】解:∵cos()=,可得:﹣sinα=,
∴sinα=﹣,
∴cos2α=1﹣2sin2α=1﹣2×(﹣)2=.
故选:B.
4.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
【考点】平面向量数量积的运算.
【分析】根据两向量垂直,数量积为0,列出方程求出t的值.
【解答】解:非零向量,满足3||=2||,<,>=60°,
∴cos<,>=,
又⊥(t+),
∴ (t+)=t +2
=t|| || +||2
=t +=0,
解得t=﹣3.
故选:B.
5.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
【考点】抛物线的简单性质.
【分析】由题意,取点M(,p),K(﹣,0),由此,即可得出结论.
【解答】解:由题意,取点M(,p),
∵K(﹣,0),
∴kKM=1,∴∠MKO=45°,
故选C.
6.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
【解答】解:作出不等式组对应的平面区域如图,则设z==,
则z的几何意义是区域内的P点与点M(﹣,0)的斜率k;
如图所示(k)min=kPA=,(k)max=kPB=4,
则的取值范围是[]
故选:A.
7.已知函数f(x)定义域为R,命题:p:f(x)为奇函数,q:
f(x)dx=0,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分必要条件的定义以及函数的奇偶性判断即可.
【解答】解:由f(x)为奇函数,得f(x)dx=0,是充分条件,
反之不成立,不是必要条件,
故选:A.
8.已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π.若将函数f(x)的图象向左平移个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
A.f(x)=2sin(x+)
B.f(x)=2sin(x+)
C.f(x)=2sin(2x+)
D.f(x)=2sin(2x+)
【考点】函数y=Asin(ωx+φ)的图象变换;由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】根据函数的图象求出函数的周期,利用函数的对称性求出ω
和φ的值即可得到结论.
【解答】解:∵函数的图象上相邻两个最高点的距离为π,
∴函数周期T=π,即T==π,即ω=2,
即f(x)=2sin(2x+φ),
若将函数f(x)的图象向左平移个单位长度后,得f(x)=2sin[2(x+)+φ)]=2sin(2x++φ),
若图象关于y轴对称.
则+φ=+kπ,
即φ=+kπ,k∈Z,
∵0<φ<π,
∴当k=0时,φ=,
即f(x)=2sin(2x+),
故选:C.
9.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
【考点】程序框图.
【分析】模拟程序的运行,依次写出每次循环得到的S,n的值,当n=5时,满足条件n>4,退出循环,输出S的值为6,即可得解.
【解答】解:模拟程序的运行,可得
S=3,n=0
不满足条件S≥5,S=6,n=1,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=2,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=3,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=4,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=5,
满足条件n>4,退出循环,输出S的值为6.
故选:C.
10.我们把各位数字之和等于6的三位数称为“吉祥数”,例如123就是一个“吉祥数”,则这样的“吉祥数”一共有( )
A.28个
B.21个
C.35个
D.56个
【考点】排列、组合及简单计数问题.
【分析】根据1+1+4=6,1+2+3=6,2+2+2=6,0+1+5=6,0+2+4=6,0+3+3=6,0+0+6=6,所以可以分为7类,分别求出每一类的三位数,再根据分类计数原理得到答案.
【解答】解:因为1+1+4=6,1+2+3=6,2+2+2=6,0+1+5=6,0+2+4=6,0+3+3=6,0+0+6=6,
所以可以分为7类,
当三个位数字为1,1,4时,三位数有3个,
当三个位数字为1,2,3时,三位数有A33=6个,
当三个位数字为2,2,2时,三位数有1个,
当三个位数字为0,1,5时,三位数有A21A22=4个,
当三个位数字为0,2,4时,三位数有A21A22=4个,
当三个位数字为0,3,3时,三位数有2个,
当三个位数字为0,0,6时,三位数有1个,
根据分类计数原理得三位数共有3+6+1+4+4+2+1=21.
故选B.
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
【考点】由三视图求面积、体积.
【分析】由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.
【解答】解:由已知中的三视图可得:
该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,
其外接球等同于棱长为2的正方体的外接球,
故2R==2,
故R=,
故选:B
12.已知函数f(x)=且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
A.(0,]
B.(一∞,]
C.(0,)
D.(一∞,)
【考点】其他不等式的解法.
【分析】分别讨论a的取值范围,利用参数分离法,结合导数研究函数的最值即可得到结论.
【解答】解:当a=0时,f(x)=﹣e﹣x<0,则不存在f(x)≤0的解集恰为[p,q],
当a<0时,f(x)<0,此时函数f(x)单调递增,则不存在f(x)≤0的解集恰为[p,q],
当a>0时,由f(x)≤0得≤e﹣x,
当x>0时,不等式等价为a≤,
设g(x)=,
则g′(x)=,
当x>1时,g′(x)<0,
当0<x<1时,g′(x)>0,
即当x=1时,g(x)取得极大值,同时也是最大值g(1)=,
∴若存在实数p,q,使得f(x)≥0的解集恰为[p,q],
则必有a<,
即0<a<,
故选:C.
二、填空题:本大题共4小题,每小题5分,共20分,请将答案填在答题卷相应横线上.
13.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
【考点】双曲线的简单性质.
【分析】求出双曲线的渐近线方程,利用渐近线与圆相切,得到a、b关系,然后求解双曲线的离心率.
【解答】解:由题意可知双曲线的渐近线方程之一为:bx+ay=0,
圆(x﹣)2+y2=1的圆心(,0),半径为1,
双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,
可得:
=1,
可得a2=b2,c=a,
∴e=.
故答案为.
14.若()a的展开式中只有第5项的二项式系数最大,则展开式中常数项是 7 .
【考点】二项式定理的应用.
【分析】根据题意,()a的展开式中只有第5项的二项式系数最大,则a=8,可得()8的二项展开式,令=0,解可得,r=6;将其代入二项展开式,可得答案.
【解答】解:根据题意,()a的展开式中只有第5项的二项式系数最大,
则a=8,
则()8的二项展开式为Tr+1=C88﹣r ()8﹣r (﹣)r=(﹣1)r ()8﹣r C88﹣r ,
令=0,解可得,r=6;
则其常数项为7.
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 2700 斛.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】由底面圆周长五丈四尺求出圆柱底面半径,根据圆柱的体积公式计算出对应的体积,除以1.62得答案.
【解答】解:设圆柱的底面半径为r,则2πr=54,r=9,
故米堆的体积为π×92×18=4374立方尺,
∵1斛米的体积约为1.62立方尺,
∴4374÷1.62≈2700斛,
故答案为2700.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,外接圆半径为1,且=,则△ABC面积的最大值为 .
【考点】三角函数中的恒等变换应用;正弦定理.
【分析】由题意,已知外接圆半径,利用正弦定理把边化角,求解出角A,根据= 2sinB 2sinC sinA=sinB sinC.转化为函数问题,利用三角函数的有界限求最值.
【解答】解:∵外接圆半径为1,
∴;
又∵=,
∴
sinAcosB=2sinCcosA﹣sinBcosA
sinC=2sinCcosA
cosA=,
∴A=,
sinA=,
那么:
= 2sinB 2sinC sinA=sinB sinC.
令y=sinB sinC.
∵,
∴y=sinB sin()=sinBcosB﹣sin2B=sin2Bcos2B﹣=sin(2B+).
∵,
∴2B+∈(,),
当2B+=时,y取最大值为.
∴△ABC面积的最大值为.
故答案为:
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.等差数列{an}前n项和为Sn,且S5=45,S6=60.
(1)求{an}的通项公式an;
(2)若数列{an}满足bn+1﹣bn=an(n∈N
)且b1=3,求{}的前n项和Tn.
【考点】等差数列的前n项和;等差数列的通项公式.
【分析】(1)利用等差数列的前n项和公式即可得出;
(2)利用“累加求和”、裂项求和、等差数列的前n项和公式即可得出.
【解答】解:(1)设等差数列{an}的公差为d,∵S5=45,S6=60,∴,解得.∴an=5+(n﹣1)×2=2n+3.
(2)∵bn+1﹣bn=an=2n+1,b1=3,
∴bn=(bn﹣bn﹣1)+(bn﹣1﹣bn﹣2)+…+(b2﹣b1)+b1
=[2(n﹣1)+3]+[2(n﹣2)+3]+…+(2×1+3)+3
=
=n2+2n.
∴=.
∴Tn=…+
=
=.
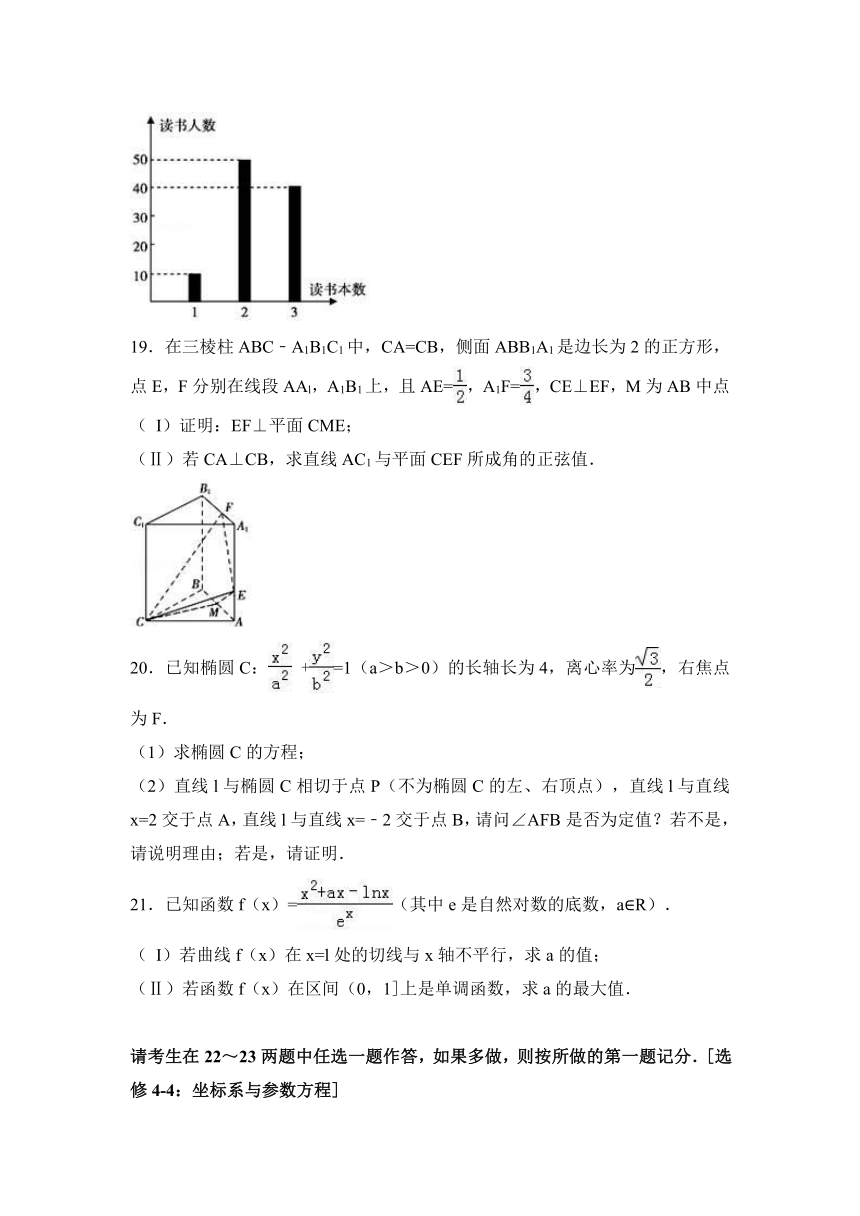
18.某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
(
I)求高一学生读课外书的人均本数;
(Ⅱ)从高一学生中任意选两名学生,求他们读课外书的本数恰好相等的概率;
(Ⅲ)从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,求随机变量ζ的分布列及数学期望E.
【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.
【分析】(Ⅰ)由图知读课外书1本、2本、3本的学生人数分别为10,50和40,由此能求出高一学生读课外书的人均本数.
(Ⅱ)从高一学生中任选两名学生,利用互斥事件概率加法公式能求出他们读课外书的本数恰好相等的概率.
(Ⅲ)从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,则ζ的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量ζ的分布列及数学期望Eζ.
【解答】解:(Ⅰ)由图知读课外书1本、2本、3本的学生人数分别为10,50和40,
∴高一学生读课外书的人均本数为:
=2.3.
(Ⅱ)从高一学生中任选两名学生,他们读课外书的本数恰好相等的概率为:
p==.
(Ⅲ)从高一学生中任选两名学生,
记“这两人中一人读1本书,另一人读2本书”为事件A,
“这两人中一人读2本书,另一人读3本书”为事件B,
“这两人中一人读1本书,另一人读3本书”为事件C,
从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,
则ζ的可能取值为0,1,2,
P(ζ=1)==,
P(ζ=1)=P(A)+P(B)=+=,
P(ζ=2)=P(C)==,
∴ζ的分布列为:
ζ
1
1
2
P
E(ζ)==.
19.在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=,A1F=,CE⊥EF,M为AB中点
(
I)证明:EF⊥平面CME;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
【考点】直线与平面所成的角;直线与平面垂直的判定.
【分析】(Ⅰ)推导出Rt△EAM∽Rt△FA1E,从而EF⊥ME,又EF⊥CE,由此能证明EF⊥平面CEM.
(Ⅱ)设线段A1B1中点为N,连结MN,推导出MC,MA,MN两两垂直,建空间直角坐标系,利用向量法能求出直线AC1与平面CEF所成角的正弦值.
【解答】证明:(Ⅰ)在正方形ABB1A1中,A1E=,AM=1,
在Rt△EAM和Rt△FA1E中,,
又∠EAM=∠FA1E=,∴Rt△EAM∽Rt△FA1E,
∴∠AEM=∠A1FE,∴EF⊥EM,
又EF⊥CE,ME∩CE=E,∴EF⊥平面CEM.
解:(Ⅱ)在等腰三角形△CAB中,
∵CA⊥CB,AB=2,∴CA=CB=,且CM=1,
设线段A1B1中点为N,连结MN,由(Ⅰ)可证CM⊥平面ABB1A1,
∴MC,MA,MN两两垂直,
建立如图所示的空间直角坐标系,
则C(1,0,0),E(0,1,),F(0,,2),A(0,1,0),C1(1,0,2),
=(﹣1,1,),=(0,﹣,),=(1,﹣1,2),
设平面CEF的法向量为=(x,y,z),
则,取z=2,得=(5,4,2),
设直线AC1与平面CEF所成角为θ,
则sinθ==,
∴直线AC1与平面CEF所成角的正弦值为.
20.已知椭圆C:
+=1(a>b>0)的长轴长为4,离心率为,右焦点为F.
(1)求椭圆C的方程;
(2)直线l与椭圆C相切于点P(不为椭圆C的左、右顶点),直线l与直线x=2交于点A,直线l与直线x=﹣2交于点B,请问∠AFB是否为定值?若不是,请说明理由;若是,请证明.
【考点】直线与圆锥曲线的关系;椭圆的标准方程.
【分析】(1)由2a=4,离心率e==,b=即可求得a和b,即可求得椭圆C的方程;
(2)l的斜率为0时,∠AFB为直角,则∠AFB为定值,当斜率不为0时,将切点代入椭圆方程,求得交点坐标,求得AF和BF的斜率kAF及kBF,即可求得kAF kBF=﹣1,即可求得∠AFB为定值.
【解答】解:(1)2a=4,即a=2,e==,
∴c=,
b==1,
∴椭圆方程为:,
(2)证明:当l的斜率为0时,∠AFB为直角,则∠AFB为定值,为,
当斜率不为0时,设切点为P(x0,y0),则l:,
∴A(2,),B(﹣2,),
∴kAF kBF= ==﹣1,
∴∠AFB为定值.
21.已知函数f(x)=(其中e是自然对数的底数,a∈R).
(
I)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(Ⅱ)若函数f(x)在区间(0,1]上是单调函数,求a的最大值.
【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.
【分析】(Ⅰ)求出原函数的导函数,可得f′(1)=0,得到曲线f(x)在x=1处的切线方程为y=,结合切线与x轴不平行,可得,从而求得a值;
(Ⅱ)由f′(x)=,设h(x)=,求出h′(x),可知h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a.
然后分当2﹣a≥0,和2﹣a<0分类研究函数的单调性得答案.
【解答】解:(Ⅰ)依题意,f′(x)=,
f′(1)=0,且曲线f(x)在x=1处的切线方程为y=,
∵切线与x轴不平行,故切线与x轴重合,∴,即a=﹣1;
(Ⅱ)f′(x)=,
设h(x)=,则h′(x)=﹣2x+(2﹣a)+.
h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a.
①当2﹣a≥0,即a≤2时,h′(x)≥0,h(x)在区间(0,1)上为增函数.
∵h(1)=0,∴h(x)≤0在(0,1]上恒成立,即f′(x)≤0在(0,1]上恒成立.
∴f(x)在(0,1]上是减函数.
∴a≤2满足题意;
②当2﹣a<0,即a>2时,设函数h′(x)的唯一零点为x1,
则h(x)在(0,x1)上递增,在(x1,1)上递减.
又∵h(1)=0,∴h(x1)>0.
又∵h(e﹣a)=﹣e﹣2a+(2﹣a)e﹣a+a﹣ea+lne﹣a=﹣e﹣2a+(2﹣a)e﹣a﹣ea<0,
∴h(x)在(0,1)内由唯一一个零点x′,
当x∈(0,x′)时,h(x)<0,当x∈(x′,1)时,h(x)>0.
从而f(x)在(0,x′)上递减,在(x′,1)上递增,与在区间(0,1]上是单调函数矛盾.
∴a>2不合题意.
综上,a的最大值为2.
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
【考点】参数方程化成普通方程.
【分析】(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程,配方可得标准方程.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1,t2.利用|PA|+|PB|=|t1﹣t2|,即可得出.
【解答】解:(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方为x2+(y﹣3)2=9.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1=,t2=﹣.
∴|PA|+|PB|=|t1﹣t2|=2.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【考点】函数恒成立问题;绝对值不等式的解法.
【分析】(1)利用||x﹣1|+2|<5,转化为﹣7<|x﹣1|<3,然后求解不等式即可.
(2)利用条件说明{y|y=f(x)} {y|y=g(x)},通过函数的最值,列出不等式求解即可.
【解答】解:(1)由||x﹣1|+2|<5,得﹣5<|x﹣1|+2<5
∴﹣7<|x﹣1|<3,
得不等式的解为﹣2<x<4…
(2)因为任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x)} {y|y=g(x)},
又f(x)=|2x﹣a|+|2x+3|≥|(2x﹣a)﹣(2x+3)|=|a+3|,
g(x)=|x﹣1|+2≥2,所以|a+3|≥2,解得a≥﹣1或a≤﹣5,
所以实数a的取值范围为a≥﹣1或a≤﹣5.…
2017年2月18日
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.已知A={x|2x<1},B={x|y=},则A∩B=( )
A.[﹣2,0)
B.[﹣2,0]
C.(0,+∞)
D.[﹣2,+∞)
2.复数Z在映射f下的象为(1+i)Z,则﹣1+2i的原象为( )
A.
B.
C.
D.
3.若cos()=,则cos2α=( )
A.
B.
C.一
D.
4.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
5.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
6.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
7.已知函数f(x)定义域为R,命题:p:f(x)为奇函数,q:
f(x)dx=0,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
8.已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π.若将函数f(x)的图象向左平移个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
A.f(x)=2sin(x+)
B.f(x)=2sin(x+)
C.f(x)=2sin(2x+)
D.f(x)=2sin(2x+)
9.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
10.我们把各位数字之和等于6的三位数称为“吉祥数”,例如123就是一个“吉祥数”,则这样的“吉祥数”一共有( )
A.28个
B.21个
C.35个
D.56个
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
12.已知函数f(x)=且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
A.(0,]
B.(一∞,]
C.(0,)
D.(一∞,)
二、填空题:本大题共4小题,每小题5分,共20分,请将答案填在答题卷相应横线上.
13.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
14.若()a的展开式中只有第5项的二项式系数最大,则展开式中常数项是 .
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 斛.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,外接圆半径为1,且=,则△ABC面积的最大值为 .
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.等差数列{an}前n项和为Sn,且S5=45,S6=60.
(1)求{an}的通项公式an;
(2)若数列{an}满足bn+1﹣bn=an(n∈N
)且b1=3,求{}的前n项和Tn.
18.某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
(
I)求高一学生读课外书的人均本数;
(Ⅱ)从高一学生中任意选两名学生,求他们读课外书的本数恰好相等的概率;
(Ⅲ)从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,求随机变量ζ的分布列及数学期望E.
19.在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=,A1F=,CE⊥EF,M为AB中点
(
I)证明:EF⊥平面CME;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
20.已知椭圆C:
+=1(a>b>0)的长轴长为4,离心率为,右焦点为F.
(1)求椭圆C的方程;
(2)直线l与椭圆C相切于点P(不为椭圆C的左、右顶点),直线l与直线x=2交于点A,直线l与直线x=﹣2交于点B,请问∠AFB是否为定值?若不是,请说明理由;若是,请证明.
21.已知函数f(x)=(其中e是自然对数的底数,a∈R).
(
I)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(Ⅱ)若函数f(x)在区间(0,1]上是单调函数,求a的最大值.
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
2017年安徽省蚌埠市高考数学一模试卷(理科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.已知A={x|2x<1},B={x|y=},则A∩B=( )
A.[﹣2,0)
B.[﹣2,0]
C.(0,+∞)
D.[﹣2,+∞)
【考点】交集及其运算.
【分析】求出集合A,B,根据集合的基本运算,即可得到结论.
【解答】解:A={x|2x<1}={x|x<0}=(﹣∞,0),
B={x|y=}=[﹣2,+∞)
∴A∩B=[﹣2,0),
故选:A.
2.复数Z在映射f下的象为(1+i)Z,则﹣1+2i的原象为( )
A.
B.
C.
D.
【考点】复数代数形式的乘除运算;映射.
【分析】先由已知,得出﹣1+2i的原象为,再化简计算即可.
【解答】解:根据题意,若设﹣1+2i的原象为复数z,则得出(1+i)z=﹣1+2i,
所以z===
故选B
3.若cos()=,则cos2α=( )
A.
B.
C.一
D.
【考点】二倍角的余弦.
【分析】由已知利用诱导公式可求sinα的值,进而利用二倍角的余弦函数公式即可计算得解.
【解答】解:∵cos()=,可得:﹣sinα=,
∴sinα=﹣,
∴cos2α=1﹣2sin2α=1﹣2×(﹣)2=.
故选:B.
4.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
【考点】平面向量数量积的运算.
【分析】根据两向量垂直,数量积为0,列出方程求出t的值.
【解答】解:非零向量,满足3||=2||,<,>=60°,
∴cos<,>=,
又⊥(t+),
∴ (t+)=t +2
=t|| || +||2
=t +=0,
解得t=﹣3.
故选:B.
5.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
【考点】抛物线的简单性质.
【分析】由题意,取点M(,p),K(﹣,0),由此,即可得出结论.
【解答】解:由题意,取点M(,p),
∵K(﹣,0),
∴kKM=1,∴∠MKO=45°,
故选C.
6.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
【解答】解:作出不等式组对应的平面区域如图,则设z==,
则z的几何意义是区域内的P点与点M(﹣,0)的斜率k;
如图所示(k)min=kPA=,(k)max=kPB=4,
则的取值范围是[]
故选:A.
7.已知函数f(x)定义域为R,命题:p:f(x)为奇函数,q:
f(x)dx=0,则p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据充分必要条件的定义以及函数的奇偶性判断即可.
【解答】解:由f(x)为奇函数,得f(x)dx=0,是充分条件,
反之不成立,不是必要条件,
故选:A.
8.已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象上相邻两个最高点的距离为π.若将函数f(x)的图象向左平移个单位长度后,所得图象关于y轴对称.则函数f(x)的解析式为( )
A.f(x)=2sin(x+)
B.f(x)=2sin(x+)
C.f(x)=2sin(2x+)
D.f(x)=2sin(2x+)
【考点】函数y=Asin(ωx+φ)的图象变换;由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】根据函数的图象求出函数的周期,利用函数的对称性求出ω
和φ的值即可得到结论.
【解答】解:∵函数的图象上相邻两个最高点的距离为π,
∴函数周期T=π,即T==π,即ω=2,
即f(x)=2sin(2x+φ),
若将函数f(x)的图象向左平移个单位长度后,得f(x)=2sin[2(x+)+φ)]=2sin(2x++φ),
若图象关于y轴对称.
则+φ=+kπ,
即φ=+kπ,k∈Z,
∵0<φ<π,
∴当k=0时,φ=,
即f(x)=2sin(2x+),
故选:C.
9.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
【考点】程序框图.
【分析】模拟程序的运行,依次写出每次循环得到的S,n的值,当n=5时,满足条件n>4,退出循环,输出S的值为6,即可得解.
【解答】解:模拟程序的运行,可得
S=3,n=0
不满足条件S≥5,S=6,n=1,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=2,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=3,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=4,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=5,
满足条件n>4,退出循环,输出S的值为6.
故选:C.
10.我们把各位数字之和等于6的三位数称为“吉祥数”,例如123就是一个“吉祥数”,则这样的“吉祥数”一共有( )
A.28个
B.21个
C.35个
D.56个
【考点】排列、组合及简单计数问题.
【分析】根据1+1+4=6,1+2+3=6,2+2+2=6,0+1+5=6,0+2+4=6,0+3+3=6,0+0+6=6,所以可以分为7类,分别求出每一类的三位数,再根据分类计数原理得到答案.
【解答】解:因为1+1+4=6,1+2+3=6,2+2+2=6,0+1+5=6,0+2+4=6,0+3+3=6,0+0+6=6,
所以可以分为7类,
当三个位数字为1,1,4时,三位数有3个,
当三个位数字为1,2,3时,三位数有A33=6个,
当三个位数字为2,2,2时,三位数有1个,
当三个位数字为0,1,5时,三位数有A21A22=4个,
当三个位数字为0,2,4时,三位数有A21A22=4个,
当三个位数字为0,3,3时,三位数有2个,
当三个位数字为0,0,6时,三位数有1个,
根据分类计数原理得三位数共有3+6+1+4+4+2+1=21.
故选B.
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
【考点】由三视图求面积、体积.
【分析】由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.
【解答】解:由已知中的三视图可得:
该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,
其外接球等同于棱长为2的正方体的外接球,
故2R==2,
故R=,
故选:B
12.已知函数f(x)=且x>0).若存在实数p,q(p<q),使得f(x)≤0的解集恰好为[p,q],则a的取值范围是( )
A.(0,]
B.(一∞,]
C.(0,)
D.(一∞,)
【考点】其他不等式的解法.
【分析】分别讨论a的取值范围,利用参数分离法,结合导数研究函数的最值即可得到结论.
【解答】解:当a=0时,f(x)=﹣e﹣x<0,则不存在f(x)≤0的解集恰为[p,q],
当a<0时,f(x)<0,此时函数f(x)单调递增,则不存在f(x)≤0的解集恰为[p,q],
当a>0时,由f(x)≤0得≤e﹣x,
当x>0时,不等式等价为a≤,
设g(x)=,
则g′(x)=,
当x>1时,g′(x)<0,
当0<x<1时,g′(x)>0,
即当x=1时,g(x)取得极大值,同时也是最大值g(1)=,
∴若存在实数p,q,使得f(x)≥0的解集恰为[p,q],
则必有a<,
即0<a<,
故选:C.
二、填空题:本大题共4小题,每小题5分,共20分,请将答案填在答题卷相应横线上.
13.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
【考点】双曲线的简单性质.
【分析】求出双曲线的渐近线方程,利用渐近线与圆相切,得到a、b关系,然后求解双曲线的离心率.
【解答】解:由题意可知双曲线的渐近线方程之一为:bx+ay=0,
圆(x﹣)2+y2=1的圆心(,0),半径为1,
双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,
可得:
=1,
可得a2=b2,c=a,
∴e=.
故答案为.
14.若()a的展开式中只有第5项的二项式系数最大,则展开式中常数项是 7 .
【考点】二项式定理的应用.
【分析】根据题意,()a的展开式中只有第5项的二项式系数最大,则a=8,可得()8的二项展开式,令=0,解可得,r=6;将其代入二项展开式,可得答案.
【解答】解:根据题意,()a的展开式中只有第5项的二项式系数最大,
则a=8,
则()8的二项展开式为Tr+1=C88﹣r ()8﹣r (﹣)r=(﹣1)r ()8﹣r C88﹣r ,
令=0,解可得,r=6;
则其常数项为7.
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 2700 斛.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】由底面圆周长五丈四尺求出圆柱底面半径,根据圆柱的体积公式计算出对应的体积,除以1.62得答案.
【解答】解:设圆柱的底面半径为r,则2πr=54,r=9,
故米堆的体积为π×92×18=4374立方尺,
∵1斛米的体积约为1.62立方尺,
∴4374÷1.62≈2700斛,
故答案为2700.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,外接圆半径为1,且=,则△ABC面积的最大值为 .
【考点】三角函数中的恒等变换应用;正弦定理.
【分析】由题意,已知外接圆半径,利用正弦定理把边化角,求解出角A,根据= 2sinB 2sinC sinA=sinB sinC.转化为函数问题,利用三角函数的有界限求最值.
【解答】解:∵外接圆半径为1,
∴;
又∵=,
∴
sinAcosB=2sinCcosA﹣sinBcosA
sinC=2sinCcosA
cosA=,
∴A=,
sinA=,
那么:
= 2sinB 2sinC sinA=sinB sinC.
令y=sinB sinC.
∵,
∴y=sinB sin()=sinBcosB﹣sin2B=sin2Bcos2B﹣=sin(2B+).
∵,
∴2B+∈(,),
当2B+=时,y取最大值为.
∴△ABC面积的最大值为.
故答案为:
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.等差数列{an}前n项和为Sn,且S5=45,S6=60.
(1)求{an}的通项公式an;
(2)若数列{an}满足bn+1﹣bn=an(n∈N
)且b1=3,求{}的前n项和Tn.
【考点】等差数列的前n项和;等差数列的通项公式.
【分析】(1)利用等差数列的前n项和公式即可得出;
(2)利用“累加求和”、裂项求和、等差数列的前n项和公式即可得出.
【解答】解:(1)设等差数列{an}的公差为d,∵S5=45,S6=60,∴,解得.∴an=5+(n﹣1)×2=2n+3.
(2)∵bn+1﹣bn=an=2n+1,b1=3,
∴bn=(bn﹣bn﹣1)+(bn﹣1﹣bn﹣2)+…+(b2﹣b1)+b1
=[2(n﹣1)+3]+[2(n﹣2)+3]+…+(2×1+3)+3
=
=n2+2n.
∴=.
∴Tn=…+
=
=.
18.某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
(
I)求高一学生读课外书的人均本数;
(Ⅱ)从高一学生中任意选两名学生,求他们读课外书的本数恰好相等的概率;
(Ⅲ)从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,求随机变量ζ的分布列及数学期望E.
【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.
【分析】(Ⅰ)由图知读课外书1本、2本、3本的学生人数分别为10,50和40,由此能求出高一学生读课外书的人均本数.
(Ⅱ)从高一学生中任选两名学生,利用互斥事件概率加法公式能求出他们读课外书的本数恰好相等的概率.
(Ⅲ)从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,则ζ的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量ζ的分布列及数学期望Eζ.
【解答】解:(Ⅰ)由图知读课外书1本、2本、3本的学生人数分别为10,50和40,
∴高一学生读课外书的人均本数为:
=2.3.
(Ⅱ)从高一学生中任选两名学生,他们读课外书的本数恰好相等的概率为:
p==.
(Ⅲ)从高一学生中任选两名学生,
记“这两人中一人读1本书,另一人读2本书”为事件A,
“这两人中一人读2本书,另一人读3本书”为事件B,
“这两人中一人读1本书,另一人读3本书”为事件C,
从高一学生中任选两名学生,用ζ表示这两人读课外书的本数之差的绝对值,
则ζ的可能取值为0,1,2,
P(ζ=1)==,
P(ζ=1)=P(A)+P(B)=+=,
P(ζ=2)=P(C)==,
∴ζ的分布列为:
ζ
1
1
2
P
E(ζ)==.
19.在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=,A1F=,CE⊥EF,M为AB中点
(
I)证明:EF⊥平面CME;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
【考点】直线与平面所成的角;直线与平面垂直的判定.
【分析】(Ⅰ)推导出Rt△EAM∽Rt△FA1E,从而EF⊥ME,又EF⊥CE,由此能证明EF⊥平面CEM.
(Ⅱ)设线段A1B1中点为N,连结MN,推导出MC,MA,MN两两垂直,建空间直角坐标系,利用向量法能求出直线AC1与平面CEF所成角的正弦值.
【解答】证明:(Ⅰ)在正方形ABB1A1中,A1E=,AM=1,
在Rt△EAM和Rt△FA1E中,,
又∠EAM=∠FA1E=,∴Rt△EAM∽Rt△FA1E,
∴∠AEM=∠A1FE,∴EF⊥EM,
又EF⊥CE,ME∩CE=E,∴EF⊥平面CEM.
解:(Ⅱ)在等腰三角形△CAB中,
∵CA⊥CB,AB=2,∴CA=CB=,且CM=1,
设线段A1B1中点为N,连结MN,由(Ⅰ)可证CM⊥平面ABB1A1,
∴MC,MA,MN两两垂直,
建立如图所示的空间直角坐标系,
则C(1,0,0),E(0,1,),F(0,,2),A(0,1,0),C1(1,0,2),
=(﹣1,1,),=(0,﹣,),=(1,﹣1,2),
设平面CEF的法向量为=(x,y,z),
则,取z=2,得=(5,4,2),
设直线AC1与平面CEF所成角为θ,
则sinθ==,
∴直线AC1与平面CEF所成角的正弦值为.
20.已知椭圆C:
+=1(a>b>0)的长轴长为4,离心率为,右焦点为F.
(1)求椭圆C的方程;
(2)直线l与椭圆C相切于点P(不为椭圆C的左、右顶点),直线l与直线x=2交于点A,直线l与直线x=﹣2交于点B,请问∠AFB是否为定值?若不是,请说明理由;若是,请证明.
【考点】直线与圆锥曲线的关系;椭圆的标准方程.
【分析】(1)由2a=4,离心率e==,b=即可求得a和b,即可求得椭圆C的方程;
(2)l的斜率为0时,∠AFB为直角,则∠AFB为定值,当斜率不为0时,将切点代入椭圆方程,求得交点坐标,求得AF和BF的斜率kAF及kBF,即可求得kAF kBF=﹣1,即可求得∠AFB为定值.
【解答】解:(1)2a=4,即a=2,e==,
∴c=,
b==1,
∴椭圆方程为:,
(2)证明:当l的斜率为0时,∠AFB为直角,则∠AFB为定值,为,
当斜率不为0时,设切点为P(x0,y0),则l:,
∴A(2,),B(﹣2,),
∴kAF kBF= ==﹣1,
∴∠AFB为定值.
21.已知函数f(x)=(其中e是自然对数的底数,a∈R).
(
I)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(Ⅱ)若函数f(x)在区间(0,1]上是单调函数,求a的最大值.
【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.
【分析】(Ⅰ)求出原函数的导函数,可得f′(1)=0,得到曲线f(x)在x=1处的切线方程为y=,结合切线与x轴不平行,可得,从而求得a值;
(Ⅱ)由f′(x)=,设h(x)=,求出h′(x),可知h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a.
然后分当2﹣a≥0,和2﹣a<0分类研究函数的单调性得答案.
【解答】解:(Ⅰ)依题意,f′(x)=,
f′(1)=0,且曲线f(x)在x=1处的切线方程为y=,
∵切线与x轴不平行,故切线与x轴重合,∴,即a=﹣1;
(Ⅱ)f′(x)=,
设h(x)=,则h′(x)=﹣2x+(2﹣a)+.
h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a.
①当2﹣a≥0,即a≤2时,h′(x)≥0,h(x)在区间(0,1)上为增函数.
∵h(1)=0,∴h(x)≤0在(0,1]上恒成立,即f′(x)≤0在(0,1]上恒成立.
∴f(x)在(0,1]上是减函数.
∴a≤2满足题意;
②当2﹣a<0,即a>2时,设函数h′(x)的唯一零点为x1,
则h(x)在(0,x1)上递增,在(x1,1)上递减.
又∵h(1)=0,∴h(x1)>0.
又∵h(e﹣a)=﹣e﹣2a+(2﹣a)e﹣a+a﹣ea+lne﹣a=﹣e﹣2a+(2﹣a)e﹣a﹣ea<0,
∴h(x)在(0,1)内由唯一一个零点x′,
当x∈(0,x′)时,h(x)<0,当x∈(x′,1)时,h(x)>0.
从而f(x)在(0,x′)上递减,在(x′,1)上递增,与在区间(0,1]上是单调函数矛盾.
∴a>2不合题意.
综上,a的最大值为2.
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
【考点】参数方程化成普通方程.
【分析】(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程,配方可得标准方程.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1,t2.利用|PA|+|PB|=|t1﹣t2|,即可得出.
【解答】解:(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方为x2+(y﹣3)2=9.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1=,t2=﹣.
∴|PA|+|PB|=|t1﹣t2|=2.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【考点】函数恒成立问题;绝对值不等式的解法.
【分析】(1)利用||x﹣1|+2|<5,转化为﹣7<|x﹣1|<3,然后求解不等式即可.
(2)利用条件说明{y|y=f(x)} {y|y=g(x)},通过函数的最值,列出不等式求解即可.
【解答】解:(1)由||x﹣1|+2|<5,得﹣5<|x﹣1|+2<5
∴﹣7<|x﹣1|<3,
得不等式的解为﹣2<x<4…
(2)因为任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x)} {y|y=g(x)},
又f(x)=|2x﹣a|+|2x+3|≥|(2x﹣a)﹣(2x+3)|=|a+3|,
g(x)=|x﹣1|+2≥2,所以|a+3|≥2,解得a≥﹣1或a≤﹣5,
所以实数a的取值范围为a≥﹣1或a≤﹣5.…
2017年2月18日
同课章节目录
