2017年安徽省蚌埠市高考数学一模试卷(文科)(解析版)
文档属性
| 名称 | 2017年安徽省蚌埠市高考数学一模试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 288.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-18 23:58:34 | ||
图片预览



文档简介
2017年安徽省蚌埠市高考数学一模试卷(文科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.全集为实数集R,M={x|﹣2≤x≤2},N={x|x<1},则( RM)∩N=( )
A.{x|x<﹣2}
B.{x|﹣2<x<1}
C.{x|x<1}
D.{x|﹣2≤x<1}
2.若复数(i为虚数单位),则z的共轭复数=( )
A.1+i
B.﹣1+i
C.l﹣i
D.﹣1一i
3.已知,则=( )
A.
B.
C.
D.
4.函数y=sin(x2)的图象大致是( )
A.
B.
C.
D.
5.“()x<1”是“>1”的( )
A.充分且不必要条件
B.必要且不充分条件
C.充要条件
D.既非充分也非必要条件
6.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
7.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
8.函数y=sin(2x+φ)(0<φ<π)的图象向右平移后关于y轴对称,则满足此条件的φ值为( )
A.
B.
C.
D.
9.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
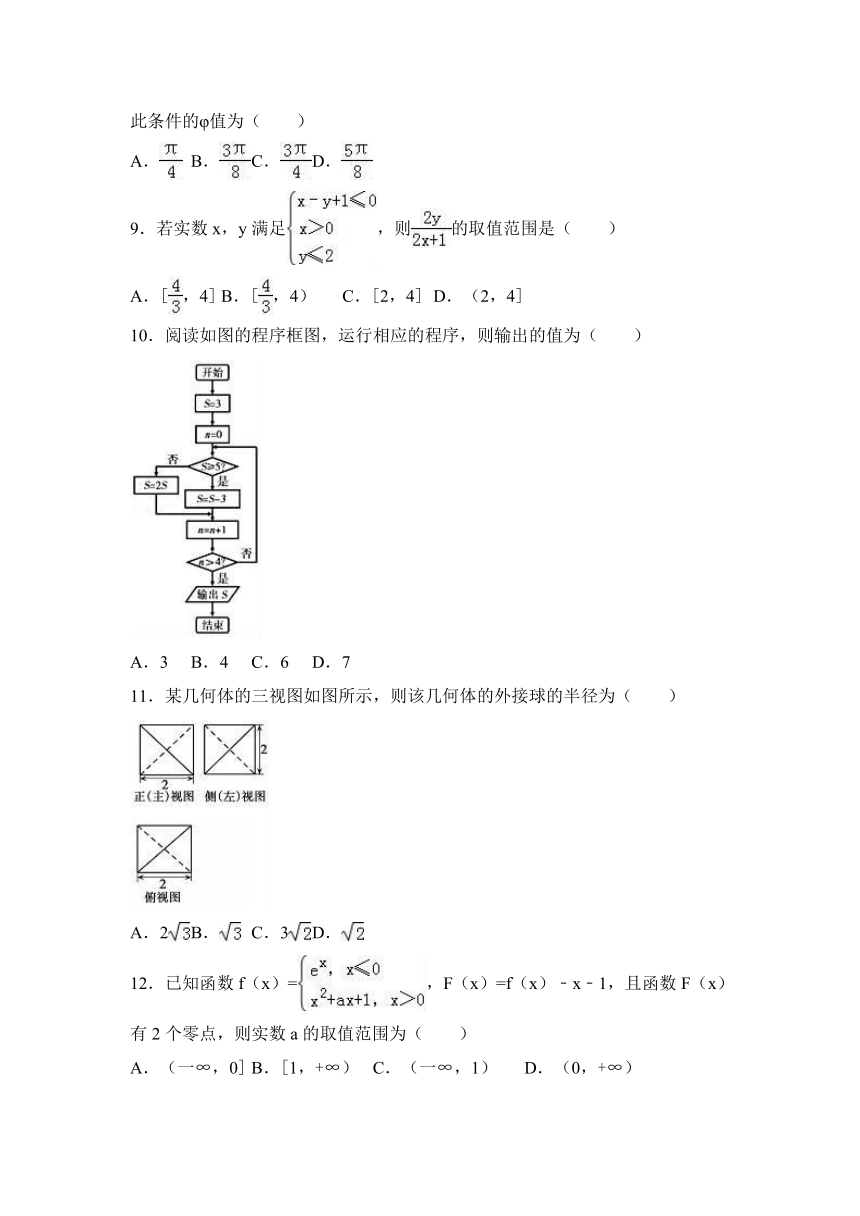
10.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
12.已知函数f(x)=,F(x)=f(x)﹣x﹣1,且函数F(x)有2个零点,则实数a的取值范围为( )
A.(一∞,0]
B.[1,+∞)
C.(一∞,1)
D.(0,+∞)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷相应横线上.
13.已知x与y之间的一组数据:
x
0
2
4
6
y
a
3
5
3a
已求得关于y与x的线性回归方程=1.2x+0.55,则a的值为 .
14.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 斛.
16.在△ABC中,角A,B,C所对的边分别为a,b,c,其中a=2,c=3,且满足(2a﹣c) cosB=b cosC,则= .
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且过点Pn(n,Sn)的切线的斜率为kn.
(I)求数列{an}的通项公式;
(Ⅱ)若bn=,求数列{bn}的前n项和Tn.
18.某公司的招聘考试有编号分别为1,2,3的三个不同的4类基本题和一道A类附加题:另有编号分别为4,5的两个不同的B类基本题和一道B类附加题.甲从这五个基本题中一次随机抽取两道题,每题做对做错及每题被抽到的概率是相等的.
(I)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”共有多少个基本事件?请列举出来;
(Ⅱ)求甲所抽取的两道基本题的编号之和小于8但不小于4的概率.
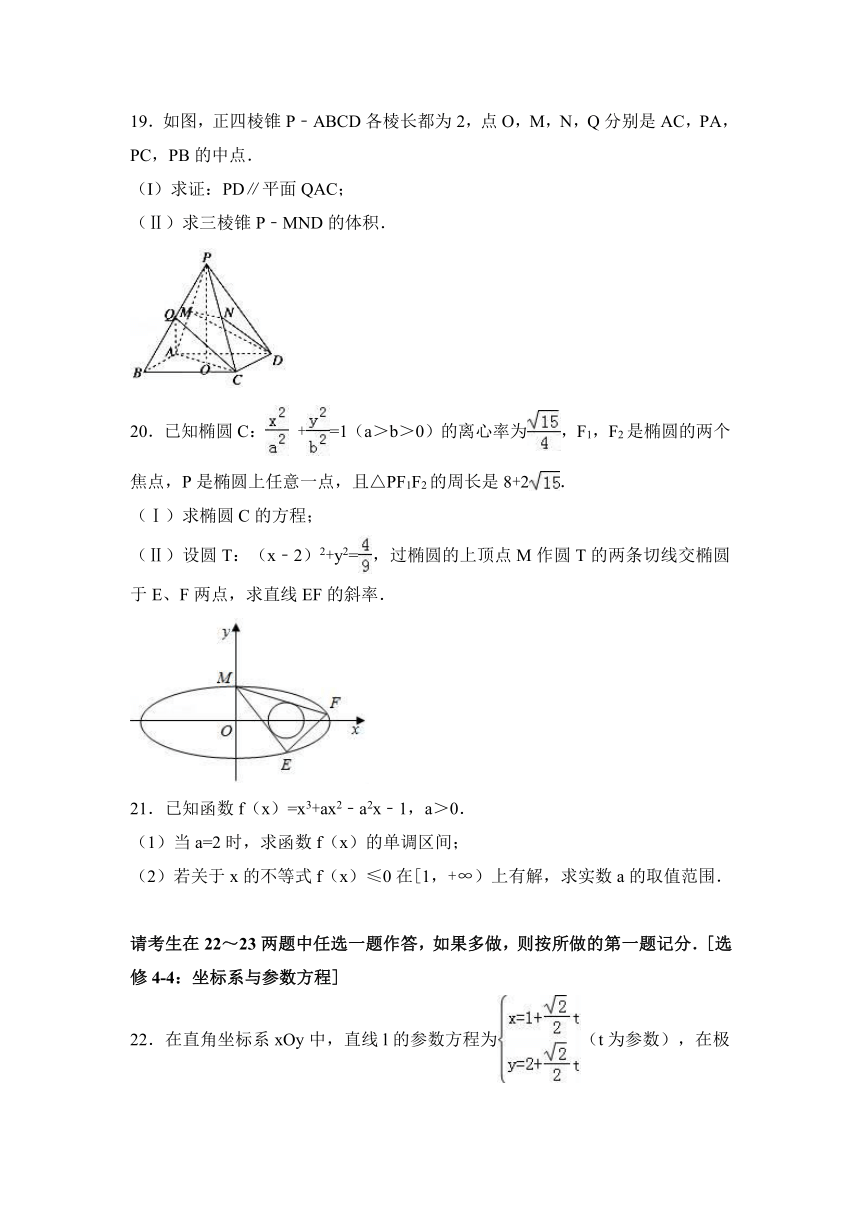
19.如图,正四棱锥P﹣ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
(I)求证:PD∥平面QAC;
(Ⅱ)求三棱锥P﹣MND的体积.
20.已知椭圆C:
+=1(a>b>0)的离心率为,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设圆T:(x﹣2)2+y2=,过椭圆的上顶点M作圆T的两条切线交椭圆于E、F两点,求直线EF的斜率.
21.已知函数f(x)=x3+ax2﹣a2x﹣1,a>0.
(1)当a=2时,求函数f(x)的单调区间;
(2)若关于x的不等式f(x)≤0在[1,+∞)上有解,求实数a的取值范围.
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
2017年安徽省蚌埠市高考数学一模试卷(文科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.全集为实数集R,M={x|﹣2≤x≤2},N={x|x<1},则( RM)∩N=( )
A.{x|x<﹣2}
B.{x|﹣2<x<1}
C.{x|x<1}
D.{x|﹣2≤x<1}
【考点】交、并、补集的混合运算.
【分析】由已知中全集为实数集R,M={x|﹣2≤x≤2},我们可以确定CRM,再根据N={x|x<1},结合集合交集的运算法则,可以求出(CRM)∩N的值.
【解答】解:∵M={x|﹣2≤x≤2},
∴CRM={x|x<﹣2,或x>2},
又∵N={x|x<1},
∴(CRM)∩N={x|x<﹣2}
故选A
2.若复数(i为虚数单位),则z的共轭复数=( )
A.1+i
B.﹣1+i
C.l﹣i
D.﹣1一i
【考点】复数代数形式的混合运算.
【分析】利用复数的运算法则、共轭复数的定义即可得出.
【解答】解:复数==﹣i﹣1,则z的共轭复数=﹣1+i.
故选:B.
3.已知,则=( )
A.
B.
C.
D.
【考点】三角函数的化简求值.
【分析】利用二倍角公式求解即可.
【解答】解:由题意:,
∴=cos2()=1﹣2sin2()=1﹣2×()2=.
故选A.
4.函数y=sin(x2)的图象大致是( )
A.
B.
C.
D.
【考点】函数的图象.
【分析】先判断函数的奇偶性,再根据特殊值即可排除.
【解答】解:因为y=f(﹣x)=sin(﹣x)2=sin(x2)=f(x),
所以y=f(x)为偶函数,
所以函数y=f(x)关于y轴对称,故排除A,C
当x=时,y=0,故排除B,
故选:D
5.“()x<1”是“>1”的( )
A.充分且不必要条件
B.必要且不充分条件
C.充要条件
D.既非充分也非必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】解不等式,根据集合的包含关系判断即可.
【解答】解:由“()x<1”,解得:x>0,
由“>1”,解得:0<x<1,
故“()x<1”是“>1”的必要不充分条件,
故选:B.
6.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
【考点】平面向量数量积的运算.
【分析】根据两向量垂直,数量积为0,列出方程求出t的值.
【解答】解:非零向量,满足3||=2||,<,>=60°,
∴cos<,>=,
又⊥(t+),
∴ (t+)=t +2
=t|| || +||2
=t +=0,
解得t=﹣3.
故选:B.
7.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
【考点】抛物线的简单性质.
【分析】由题意,取点M(,p),K(﹣,0),由此,即可得出结论.
【解答】解:由题意,取点M(,p),
∵K(﹣,0),
∴kKM=1,∴∠MKO=45°,
故选C.
8.函数y=sin(2x+φ)(0<φ<π)的图象向右平移后关于y轴对称,则满足此条件的φ值为( )
A.
B.
C.
D.
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,求得φ的值.
【解答】解:函数y=sin(2x+φ)(0<φ<π)的图象向右平移后,得到函数y=sin[2(x﹣)+φ]=sin(2x﹣+φ)的图象,
再根据所得图象关于y轴对称,可得﹣+φ=kπ+,求得φ=kπ+,k∈Z,
则满足此条件的φ=,
故选:C.
9.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
【解答】解:作出不等式组对应的平面区域如图,则设z==,
则z的几何意义是区域内的P点与点M(﹣,0)的斜率k;
如图所示(k)min=kPA=,(k)max=kPB=4,
则的取值范围是[]
故选:A.
10.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
【考点】程序框图.
【分析】模拟程序的运行,依次写出每次循环得到的S,n的值,当n=5时,满足条件n>4,退出循环,输出S的值为6,即可得解.
【解答】解:模拟程序的运行,可得
S=3,n=0
不满足条件S≥5,S=6,n=1,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=2,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=3,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=4,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=5,
满足条件n>4,退出循环,输出S的值为6.
故选:C.
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
【考点】由三视图求面积、体积.
【分析】由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.
【解答】解:由已知中的三视图可得:
该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,
其外接球等同于棱长为2的正方体的外接球,
故2R==2,
故R=,
故选:B
12.已知函数f(x)=,F(x)=f(x)﹣x﹣1,且函数F(x)有2个零点,则实数a的取值范围为( )
A.(一∞,0]
B.[1,+∞)
C.(一∞,1)
D.(0,+∞)
【考点】函数零点的判定定理.
【分析】作出函数的图象,x≤0,F(x)=ex﹣x﹣1,有一个零点0,x>0,F(x)=x[x+(a﹣1)],0是其中一个零点,利用函数F(x)有2个零点,可得1﹣a>0,即可求出实数a的取值范围.
【解答】解:由题意,x≤0,F(x)=ex﹣x﹣1,有一个零点0,
x>0,F(x)=x[x+(a﹣1)],0是其中一个零点,
∵函数F(x)有2个零点,
∴1﹣a>0,∴a<1.
故选C.
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷相应横线上.
13.已知x与y之间的一组数据:
x
0
2
4
6
y
a
3
5
3a
已求得关于y与x的线性回归方程=1.2x+0.55,则a的值为 2.15 .
【考点】线性回归方程.
【分析】首先求出这组数据的横标和纵标的平均数,写出这组数据的样本中心点,把样本中心点代入线性回归方程求出a的值.
【解答】解:
=3,
=a+2,
将(3,a+2)带入方程得:
a+2=3.6+0.55,解得:a=2.15,
故答案为:2.15.
14.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
【考点】双曲线的简单性质.
【分析】求出双曲线的渐近线方程,利用渐近线与圆相切,得到a、b关系,然后求解双曲线的离心率.
【解答】解:由题意可知双曲线的渐近线方程之一为:bx+ay=0,
圆(x﹣)2+y2=1的圆心(,0),半径为1,
双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,
可得:
=1,
可得a2=b2,c=a,
∴e=.
故答案为.
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 2700 斛.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】由底面圆周长五丈四尺求出圆柱底面半径,根据圆柱的体积公式计算出对应的体积,除以1.62得答案.
【解答】解:设圆柱的底面半径为r,则2πr=54,r=9,
故米堆的体积为π×92×18=4374立方尺,
∵1斛米的体积约为1.62立方尺,
∴4374÷1.62≈2700斛,
故答案为2700.
16.在△ABC中,角A,B,C所对的边分别为a,b,c,其中a=2,c=3,且满足(2a﹣c) cosB=b cosC,则= ﹣3 .
【考点】余弦定理的应用.
【分析】通过正弦定理把a,c,b换成sinA,sinB,sinC代入(2a﹣c) cosB=b cosC,求得B,再根据向量积性质,求得结果.
【解答】解:∵(2a﹣c)cosB=bcosC
根据正弦定理得:
(2sinA﹣sinC)cosB=sinBcosC
2sinAcosB=sinBcosC+sinCcosB
2sinAcosB=sin(B+C)
2sinAcosB=sinA
∴cosB=
∴B=60°
∴=﹣cosB=﹣(2×3×)=﹣3
故答案为:﹣3
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且过点Pn(n,Sn)的切线的斜率为kn.
(I)求数列{an}的通项公式;
(Ⅱ)若bn=,求数列{bn}的前n项和Tn.
【考点】数列的求和;数列递推式.
【分析】(I)由点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,可得Sn=n2+2n,利用递推关系可得an.
(II)f′(x)=2x+2,过点Pn(n,Sn)的切线的斜率为k.可得kn=2n+2.bn===,再利用“裂项求和”方法即可得出.
【解答】解:(I)∵点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,∴Sn=n2+2n,
n=1时,a1=3;n≥2,an=Sn﹣Sn﹣1=n2+2n﹣[(n﹣1)2+2(n﹣1)]=2n+1.
当n=1时上式也成立,∴an=2n+1.
(II)f′(x)=2x+2,过点Pn(n,Sn)的切线的斜率为k.
∴kn=2n+2.∴bn===,
∴数列{bn}的前n项和Tn=++…+
==.
18.某公司的招聘考试有编号分别为1,2,3的三个不同的4类基本题和一道A类附加题:另有编号分别为4,5的两个不同的B类基本题和一道B类附加题.甲从这五个基本题中一次随机抽取两道题,每题做对做错及每题被抽到的概率是相等的.
(I)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”共有多少个基本事件?请列举出来;
(Ⅱ)求甲所抽取的两道基本题的编号之和小于8但不小于4的概率.
【考点】列举法计算基本事件数及事件发生的概率.
【分析】(Ⅰ)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”共有10个基本事件,利用列举法能求出结果.
(Ⅱ)设事件A表示“甲所抽取的两道基本题的编号之和小于8但不小于4”,则事件A共含有7个基本事件,由此能求出甲所抽取的两道基本题的编号之和小于8但不小于4的概率.
【解答】解:(Ⅰ)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,
且x<y”共有10个基本事件,
分别为:(1,2),(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),(3,4),(3,5),(4,5).
(Ⅱ)设事件A表示“甲所抽取的两道基本题的编号之和小于8但不小于4”,
则事件A共含有7个基本事件,列举如下:
(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),
∴甲所抽取的两道基本题的编号之和小于8但不小于4的概率P(A)=.
19.如图,正四棱锥P﹣ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
(I)求证:PD∥平面QAC;
(Ⅱ)求三棱锥P﹣MND的体积.
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.
【分析】(Ⅰ)连结BD,交AC于O,连结QO,则QO∥PD,由此能证明PD∥平面QAC.
(Ⅱ)∴三棱锥P﹣MND的体积VP﹣MND=VD﹣PMN=,由此能求出结果.
【解答】证明:(Ⅰ)连结BD,交AC于O,连结QO,
∵正四棱锥P﹣ABCD中,ABCD是正方形,∴O是BD中点,
∵Q是PB中点,∴QO∥PD,
∵QO 平面QAC,PD 平面QAC,
∴PD∥平面QAC.
解:(Ⅱ)∵正四棱锥P﹣ABCD各棱长都为2,
点O,M,N,Q分别是AC,PA,PC,PB的中点,
∴AC=,PO==,
∴三棱锥P﹣MND的体积:
VP﹣MND=VD﹣PMN===.
20.已知椭圆C:
+=1(a>b>0)的离心率为,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设圆T:(x﹣2)2+y2=,过椭圆的上顶点M作圆T的两条切线交椭圆于E、F两点,求直线EF的斜率.
【考点】椭圆的简单性质.
【分析】(1)由椭圆离心率得到a,c的关系,再由△PF1F2的周长,得a,c的另一关系,联立求得a,c的值,代入隐含条件求得b,则椭圆方程可求;
(Ⅱ)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,由直线y=kx+1与圆T相切可知=,即32k2+36k+5=0,由根与系数关系得到k1+k2=﹣,k1k2=,再联立一切线方程和椭圆方程,求得E的坐标,同理求得F坐标,利用斜率公式得到kEF.
【解答】解:(Ⅰ)由题意,e===,可知a=4b,c=b,
∵△PF1F2的周长是8+2,∴2a+2c=8+2,
∴a=4,b=1,
∴所求椭圆方程为+y2=1
…
(Ⅱ)椭圆的上顶点为M(0,1),由题知过点M与圆T相切的直线有斜率,
则设其方程为l:y=kx+1,由直线y=kx+1与圆T相切可知=,
即32k2+36k+5=0,∴k1+k2=﹣,k1k2=,…
由得(1+16k12)x2+32k1x=0,
∴xE=﹣.
同理xF=﹣
…
kEF====
故直线EF的斜率为.…
21.已知函数f(x)=x3+ax2﹣a2x﹣1,a>0.
(1)当a=2时,求函数f(x)的单调区间;
(2)若关于x的不等式f(x)≤0在[1,+∞)上有解,求实数a的取值范围.
【考点】利用导数研究函数的单调性.
【分析】(1)由当a=2时,f(x)=x3+2x2﹣4x﹣1,求导:f′(x)=3x2+4x2﹣4=(3x﹣2)(x+2),f′(x)=0,解得:x=,x=﹣2,令f′(x)>0,求得函数的单调递增区间,令f′(x)<0,求得函数的单调递减区间;
(2)由题意可知:f(x)在区间[1,+∞)上的最小值小于等于0,求导f′(x)=3x2+2ax2﹣22=(3x﹣a)(x+a),令f′(x)=0,解得:x1=>0,x2=﹣a<0,①当≤1,即a≤3时,由函数的单调性可知:当x=1时取最小值,即f(1)≤0,即可求得a的取值范围;当>1,即a>3时,则当x=时,取最小值,f()=+﹣﹣1≤0,即可求得实数a的取值范围.
【解答】解:(1)当a=2时,函数f(x)=x3+2x2﹣4x﹣1,
求导:f′(x)=3x2+4x2﹣4=(3x﹣2)(x+2),
令f′(x)=0,解得:x=,x=﹣2,
由f′(x)>0,解得:x>或x<﹣2,
由f′(x)<0,解得:﹣2<x<,
∴函数f(x)的单调递减区间为(﹣2,),单调递增区间(﹣∞,﹣2),(,+∞);
(2)要使f(x)≤0在[1,+∞)上有解,只要f(x)在区间[1,+∞)上的最小值小于等于0,
由f′(x)=3x2+2ax2﹣22=(3x﹣a)(x+a),
令f′(x)=0,解得:x1=>0,x2=﹣a<0,
①当≤1,即a≤3时,f(x)在区间[1,+∞)上单调递增,
∴f(x)在[1,+∞)上的最小值为f(1),
由f(1)≤0,即1+a﹣a2﹣1≤0,整理得:a2﹣a≥0,
解得:a≥1或a≤0,
∴1≤a≤3.
②当>1,即a>3时,f(x)在区间[1,]上单调递减,在[,+∞)上单调递增,
∴f(x)在[1,+∞)上最小值为f(),
由f()=+﹣﹣1≤0,解得:a≥,
∴a>3.
综上可知,实数a的取值范围是[1,+∞).
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
【考点】参数方程化成普通方程.
【分析】(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程,配方可得标准方程.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1,t2.利用|PA|+|PB|=|t1﹣t2|,即可得出.
【解答】解:(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方为x2+(y﹣3)2=9.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1=,t2=﹣.
∴|PA|+|PB|=|t1﹣t2|=2.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【考点】函数恒成立问题;绝对值不等式的解法.
【分析】(1)利用||x﹣1|+2|<5,转化为﹣7<|x﹣1|<3,然后求解不等式即可.
(2)利用条件说明{y|y=f(x)} {y|y=g(x)},通过函数的最值,列出不等式求解即可.
【解答】解:(1)由||x﹣1|+2|<5,得﹣5<|x﹣1|+2<5
∴﹣7<|x﹣1|<3,
得不等式的解为﹣2<x<4…
(2)因为任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x)} {y|y=g(x)},
又f(x)=|2x﹣a|+|2x+3|≥|(2x﹣a)﹣(2x+3)|=|a+3|,
g(x)=|x﹣1|+2≥2,所以|a+3|≥2,解得a≥﹣1或a≤﹣5,
所以实数a的取值范围为a≥﹣1或a≤﹣5.…
2017年2月18日
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.全集为实数集R,M={x|﹣2≤x≤2},N={x|x<1},则( RM)∩N=( )
A.{x|x<﹣2}
B.{x|﹣2<x<1}
C.{x|x<1}
D.{x|﹣2≤x<1}
2.若复数(i为虚数单位),则z的共轭复数=( )
A.1+i
B.﹣1+i
C.l﹣i
D.﹣1一i
3.已知,则=( )
A.
B.
C.
D.
4.函数y=sin(x2)的图象大致是( )
A.
B.
C.
D.
5.“()x<1”是“>1”的( )
A.充分且不必要条件
B.必要且不充分条件
C.充要条件
D.既非充分也非必要条件
6.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
7.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
8.函数y=sin(2x+φ)(0<φ<π)的图象向右平移后关于y轴对称,则满足此条件的φ值为( )
A.
B.
C.
D.
9.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
10.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
12.已知函数f(x)=,F(x)=f(x)﹣x﹣1,且函数F(x)有2个零点,则实数a的取值范围为( )
A.(一∞,0]
B.[1,+∞)
C.(一∞,1)
D.(0,+∞)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷相应横线上.
13.已知x与y之间的一组数据:
x
0
2
4
6
y
a
3
5
3a
已求得关于y与x的线性回归方程=1.2x+0.55,则a的值为 .
14.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 斛.
16.在△ABC中,角A,B,C所对的边分别为a,b,c,其中a=2,c=3,且满足(2a﹣c) cosB=b cosC,则= .
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且过点Pn(n,Sn)的切线的斜率为kn.
(I)求数列{an}的通项公式;
(Ⅱ)若bn=,求数列{bn}的前n项和Tn.
18.某公司的招聘考试有编号分别为1,2,3的三个不同的4类基本题和一道A类附加题:另有编号分别为4,5的两个不同的B类基本题和一道B类附加题.甲从这五个基本题中一次随机抽取两道题,每题做对做错及每题被抽到的概率是相等的.
(I)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”共有多少个基本事件?请列举出来;
(Ⅱ)求甲所抽取的两道基本题的编号之和小于8但不小于4的概率.
19.如图,正四棱锥P﹣ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
(I)求证:PD∥平面QAC;
(Ⅱ)求三棱锥P﹣MND的体积.
20.已知椭圆C:
+=1(a>b>0)的离心率为,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设圆T:(x﹣2)2+y2=,过椭圆的上顶点M作圆T的两条切线交椭圆于E、F两点,求直线EF的斜率.
21.已知函数f(x)=x3+ax2﹣a2x﹣1,a>0.
(1)当a=2时,求函数f(x)的单调区间;
(2)若关于x的不等式f(x)≤0在[1,+∞)上有解,求实数a的取值范围.
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
2017年安徽省蚌埠市高考数学一模试卷(文科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的A,B,C,D的四个选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号涂到答题卷相应位置.
1.全集为实数集R,M={x|﹣2≤x≤2},N={x|x<1},则( RM)∩N=( )
A.{x|x<﹣2}
B.{x|﹣2<x<1}
C.{x|x<1}
D.{x|﹣2≤x<1}
【考点】交、并、补集的混合运算.
【分析】由已知中全集为实数集R,M={x|﹣2≤x≤2},我们可以确定CRM,再根据N={x|x<1},结合集合交集的运算法则,可以求出(CRM)∩N的值.
【解答】解:∵M={x|﹣2≤x≤2},
∴CRM={x|x<﹣2,或x>2},
又∵N={x|x<1},
∴(CRM)∩N={x|x<﹣2}
故选A
2.若复数(i为虚数单位),则z的共轭复数=( )
A.1+i
B.﹣1+i
C.l﹣i
D.﹣1一i
【考点】复数代数形式的混合运算.
【分析】利用复数的运算法则、共轭复数的定义即可得出.
【解答】解:复数==﹣i﹣1,则z的共轭复数=﹣1+i.
故选:B.
3.已知,则=( )
A.
B.
C.
D.
【考点】三角函数的化简求值.
【分析】利用二倍角公式求解即可.
【解答】解:由题意:,
∴=cos2()=1﹣2sin2()=1﹣2×()2=.
故选A.
4.函数y=sin(x2)的图象大致是( )
A.
B.
C.
D.
【考点】函数的图象.
【分析】先判断函数的奇偶性,再根据特殊值即可排除.
【解答】解:因为y=f(﹣x)=sin(﹣x)2=sin(x2)=f(x),
所以y=f(x)为偶函数,
所以函数y=f(x)关于y轴对称,故排除A,C
当x=时,y=0,故排除B,
故选:D
5.“()x<1”是“>1”的( )
A.充分且不必要条件
B.必要且不充分条件
C.充要条件
D.既非充分也非必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】解不等式,根据集合的包含关系判断即可.
【解答】解:由“()x<1”,解得:x>0,
由“>1”,解得:0<x<1,
故“()x<1”是“>1”的必要不充分条件,
故选:B.
6.已知非零向量,满足3||=2||,<,>=60°,若⊥(t+)则实数t的值为( )
A.3
B.﹣3
C.2
D.﹣2
【考点】平面向量数量积的运算.
【分析】根据两向量垂直,数量积为0,列出方程求出t的值.
【解答】解:非零向量,满足3||=2||,<,>=60°,
∴cos<,>=,
又⊥(t+),
∴ (t+)=t +2
=t|| || +||2
=t +=0,
解得t=﹣3.
故选:B.
7.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
A.15°
B.30°
C.45°
D.60°
【考点】抛物线的简单性质.
【分析】由题意,取点M(,p),K(﹣,0),由此,即可得出结论.
【解答】解:由题意,取点M(,p),
∵K(﹣,0),
∴kKM=1,∴∠MKO=45°,
故选C.
8.函数y=sin(2x+φ)(0<φ<π)的图象向右平移后关于y轴对称,则满足此条件的φ值为( )
A.
B.
C.
D.
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,求得φ的值.
【解答】解:函数y=sin(2x+φ)(0<φ<π)的图象向右平移后,得到函数y=sin[2(x﹣)+φ]=sin(2x﹣+φ)的图象,
再根据所得图象关于y轴对称,可得﹣+φ=kπ+,求得φ=kπ+,k∈Z,
则满足此条件的φ=,
故选:C.
9.若实数x,y满足,则的取值范围是( )
A.[,4]
B.[,4)
C.[2,4]
D.(2,4]
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用直线斜率的几何意义进行求解即可.
【解答】解:作出不等式组对应的平面区域如图,则设z==,
则z的几何意义是区域内的P点与点M(﹣,0)的斜率k;
如图所示(k)min=kPA=,(k)max=kPB=4,
则的取值范围是[]
故选:A.
10.阅读如图的程序框图,运行相应的程序,则输出的值为( )
A.3
B.4
C.6
D.7
【考点】程序框图.
【分析】模拟程序的运行,依次写出每次循环得到的S,n的值,当n=5时,满足条件n>4,退出循环,输出S的值为6,即可得解.
【解答】解:模拟程序的运行,可得
S=3,n=0
不满足条件S≥5,S=6,n=1,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=2,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=3,
不满足条件n>4,执行循环体,满足条件S≥5,S=3,n=4,
不满足条件n>4,执行循环体,不满足条件S≥5,S=6,n=5,
满足条件n>4,退出循环,输出S的值为6.
故选:C.
11.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
A.2
B.
C.3
D.
【考点】由三视图求面积、体积.
【分析】由已知中的三视图可得:该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,其外接球等同于棱长为2的正方体的外接球,进而得到答案.
【解答】解:由已知中的三视图可得:
该几何体是一个棱长为2的正方体,切去四个角所得的正四面体,
其外接球等同于棱长为2的正方体的外接球,
故2R==2,
故R=,
故选:B
12.已知函数f(x)=,F(x)=f(x)﹣x﹣1,且函数F(x)有2个零点,则实数a的取值范围为( )
A.(一∞,0]
B.[1,+∞)
C.(一∞,1)
D.(0,+∞)
【考点】函数零点的判定定理.
【分析】作出函数的图象,x≤0,F(x)=ex﹣x﹣1,有一个零点0,x>0,F(x)=x[x+(a﹣1)],0是其中一个零点,利用函数F(x)有2个零点,可得1﹣a>0,即可求出实数a的取值范围.
【解答】解:由题意,x≤0,F(x)=ex﹣x﹣1,有一个零点0,
x>0,F(x)=x[x+(a﹣1)],0是其中一个零点,
∵函数F(x)有2个零点,
∴1﹣a>0,∴a<1.
故选C.
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷相应横线上.
13.已知x与y之间的一组数据:
x
0
2
4
6
y
a
3
5
3a
已求得关于y与x的线性回归方程=1.2x+0.55,则a的值为 2.15 .
【考点】线性回归方程.
【分析】首先求出这组数据的横标和纵标的平均数,写出这组数据的样本中心点,把样本中心点代入线性回归方程求出a的值.
【解答】解:
=3,
=a+2,
将(3,a+2)带入方程得:
a+2=3.6+0.55,解得:a=2.15,
故答案为:2.15.
14.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,则此双曲线的离心率为 .
【考点】双曲线的简单性质.
【分析】求出双曲线的渐近线方程,利用渐近线与圆相切,得到a、b关系,然后求解双曲线的离心率.
【解答】解:由题意可知双曲线的渐近线方程之一为:bx+ay=0,
圆(x﹣)2+y2=1的圆心(,0),半径为1,
双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣)2+y2=1相切,
可得:
=1,
可得a2=b2,c=a,
∴e=.
故答案为.
15.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能放多少斛米”(古制1丈=10尺,1斛=1.62立方尺,圆周率π=3),则该圆柱形容器能放米 2700 斛.
【考点】旋转体(圆柱、圆锥、圆台).
【分析】由底面圆周长五丈四尺求出圆柱底面半径,根据圆柱的体积公式计算出对应的体积,除以1.62得答案.
【解答】解:设圆柱的底面半径为r,则2πr=54,r=9,
故米堆的体积为π×92×18=4374立方尺,
∵1斛米的体积约为1.62立方尺,
∴4374÷1.62≈2700斛,
故答案为2700.
16.在△ABC中,角A,B,C所对的边分别为a,b,c,其中a=2,c=3,且满足(2a﹣c) cosB=b cosC,则= ﹣3 .
【考点】余弦定理的应用.
【分析】通过正弦定理把a,c,b换成sinA,sinB,sinC代入(2a﹣c) cosB=b cosC,求得B,再根据向量积性质,求得结果.
【解答】解:∵(2a﹣c)cosB=bcosC
根据正弦定理得:
(2sinA﹣sinC)cosB=sinBcosC
2sinAcosB=sinBcosC+sinCcosB
2sinAcosB=sin(B+C)
2sinAcosB=sinA
∴cosB=
∴B=60°
∴=﹣cosB=﹣(2×3×)=﹣3
故答案为:﹣3
三、解答题:本大题共5小题,共70分.解答须写出说明、证明过程和演算步骤.
17.已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且过点Pn(n,Sn)的切线的斜率为kn.
(I)求数列{an}的通项公式;
(Ⅱ)若bn=,求数列{bn}的前n项和Tn.
【考点】数列的求和;数列递推式.
【分析】(I)由点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,可得Sn=n2+2n,利用递推关系可得an.
(II)f′(x)=2x+2,过点Pn(n,Sn)的切线的斜率为k.可得kn=2n+2.bn===,再利用“裂项求和”方法即可得出.
【解答】解:(I)∵点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,∴Sn=n2+2n,
n=1时,a1=3;n≥2,an=Sn﹣Sn﹣1=n2+2n﹣[(n﹣1)2+2(n﹣1)]=2n+1.
当n=1时上式也成立,∴an=2n+1.
(II)f′(x)=2x+2,过点Pn(n,Sn)的切线的斜率为k.
∴kn=2n+2.∴bn===,
∴数列{bn}的前n项和Tn=++…+
==.
18.某公司的招聘考试有编号分别为1,2,3的三个不同的4类基本题和一道A类附加题:另有编号分别为4,5的两个不同的B类基本题和一道B类附加题.甲从这五个基本题中一次随机抽取两道题,每题做对做错及每题被抽到的概率是相等的.
(I)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”共有多少个基本事件?请列举出来;
(Ⅱ)求甲所抽取的两道基本题的编号之和小于8但不小于4的概率.
【考点】列举法计算基本事件数及事件发生的概率.
【分析】(Ⅰ)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且x<y”共有10个基本事件,利用列举法能求出结果.
(Ⅱ)设事件A表示“甲所抽取的两道基本题的编号之和小于8但不小于4”,则事件A共含有7个基本事件,由此能求出甲所抽取的两道基本题的编号之和小于8但不小于4的概率.
【解答】解:(Ⅰ)用符号(x,y)表示事件“抽到的两题的编号分别为x、y,
且x<y”共有10个基本事件,
分别为:(1,2),(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),(3,4),(3,5),(4,5).
(Ⅱ)设事件A表示“甲所抽取的两道基本题的编号之和小于8但不小于4”,
则事件A共含有7个基本事件,列举如下:
(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),
∴甲所抽取的两道基本题的编号之和小于8但不小于4的概率P(A)=.
19.如图,正四棱锥P﹣ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
(I)求证:PD∥平面QAC;
(Ⅱ)求三棱锥P﹣MND的体积.
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.
【分析】(Ⅰ)连结BD,交AC于O,连结QO,则QO∥PD,由此能证明PD∥平面QAC.
(Ⅱ)∴三棱锥P﹣MND的体积VP﹣MND=VD﹣PMN=,由此能求出结果.
【解答】证明:(Ⅰ)连结BD,交AC于O,连结QO,
∵正四棱锥P﹣ABCD中,ABCD是正方形,∴O是BD中点,
∵Q是PB中点,∴QO∥PD,
∵QO 平面QAC,PD 平面QAC,
∴PD∥平面QAC.
解:(Ⅱ)∵正四棱锥P﹣ABCD各棱长都为2,
点O,M,N,Q分别是AC,PA,PC,PB的中点,
∴AC=,PO==,
∴三棱锥P﹣MND的体积:
VP﹣MND=VD﹣PMN===.
20.已知椭圆C:
+=1(a>b>0)的离心率为,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设圆T:(x﹣2)2+y2=,过椭圆的上顶点M作圆T的两条切线交椭圆于E、F两点,求直线EF的斜率.
【考点】椭圆的简单性质.
【分析】(1)由椭圆离心率得到a,c的关系,再由△PF1F2的周长,得a,c的另一关系,联立求得a,c的值,代入隐含条件求得b,则椭圆方程可求;
(Ⅱ)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,由直线y=kx+1与圆T相切可知=,即32k2+36k+5=0,由根与系数关系得到k1+k2=﹣,k1k2=,再联立一切线方程和椭圆方程,求得E的坐标,同理求得F坐标,利用斜率公式得到kEF.
【解答】解:(Ⅰ)由题意,e===,可知a=4b,c=b,
∵△PF1F2的周长是8+2,∴2a+2c=8+2,
∴a=4,b=1,
∴所求椭圆方程为+y2=1
…
(Ⅱ)椭圆的上顶点为M(0,1),由题知过点M与圆T相切的直线有斜率,
则设其方程为l:y=kx+1,由直线y=kx+1与圆T相切可知=,
即32k2+36k+5=0,∴k1+k2=﹣,k1k2=,…
由得(1+16k12)x2+32k1x=0,
∴xE=﹣.
同理xF=﹣
…
kEF====
故直线EF的斜率为.…
21.已知函数f(x)=x3+ax2﹣a2x﹣1,a>0.
(1)当a=2时,求函数f(x)的单调区间;
(2)若关于x的不等式f(x)≤0在[1,+∞)上有解,求实数a的取值范围.
【考点】利用导数研究函数的单调性.
【分析】(1)由当a=2时,f(x)=x3+2x2﹣4x﹣1,求导:f′(x)=3x2+4x2﹣4=(3x﹣2)(x+2),f′(x)=0,解得:x=,x=﹣2,令f′(x)>0,求得函数的单调递增区间,令f′(x)<0,求得函数的单调递减区间;
(2)由题意可知:f(x)在区间[1,+∞)上的最小值小于等于0,求导f′(x)=3x2+2ax2﹣22=(3x﹣a)(x+a),令f′(x)=0,解得:x1=>0,x2=﹣a<0,①当≤1,即a≤3时,由函数的单调性可知:当x=1时取最小值,即f(1)≤0,即可求得a的取值范围;当>1,即a>3时,则当x=时,取最小值,f()=+﹣﹣1≤0,即可求得实数a的取值范围.
【解答】解:(1)当a=2时,函数f(x)=x3+2x2﹣4x﹣1,
求导:f′(x)=3x2+4x2﹣4=(3x﹣2)(x+2),
令f′(x)=0,解得:x=,x=﹣2,
由f′(x)>0,解得:x>或x<﹣2,
由f′(x)<0,解得:﹣2<x<,
∴函数f(x)的单调递减区间为(﹣2,),单调递增区间(﹣∞,﹣2),(,+∞);
(2)要使f(x)≤0在[1,+∞)上有解,只要f(x)在区间[1,+∞)上的最小值小于等于0,
由f′(x)=3x2+2ax2﹣22=(3x﹣a)(x+a),
令f′(x)=0,解得:x1=>0,x2=﹣a<0,
①当≤1,即a≤3时,f(x)在区间[1,+∞)上单调递增,
∴f(x)在[1,+∞)上的最小值为f(1),
由f(1)≤0,即1+a﹣a2﹣1≤0,整理得:a2﹣a≥0,
解得:a≥1或a≤0,
∴1≤a≤3.
②当>1,即a>3时,f(x)在区间[1,]上单调递减,在[,+∞)上单调递增,
∴f(x)在[1,+∞)上最小值为f(),
由f()=+﹣﹣1≤0,解得:a≥,
∴a>3.
综上可知,实数a的取值范围是[1,+∞).
请考生在22~23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]
22.在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.
(
I)求直角坐标下圆C的标准方程;
(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.
【考点】参数方程化成普通方程.
【分析】(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程,配方可得标准方程.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1,t2.利用|PA|+|PB|=|t1﹣t2|,即可得出.
【解答】解:(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方为x2+(y﹣3)2=9.
(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1=,t2=﹣.
∴|PA|+|PB|=|t1﹣t2|=2.
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
【考点】函数恒成立问题;绝对值不等式的解法.
【分析】(1)利用||x﹣1|+2|<5,转化为﹣7<|x﹣1|<3,然后求解不等式即可.
(2)利用条件说明{y|y=f(x)} {y|y=g(x)},通过函数的最值,列出不等式求解即可.
【解答】解:(1)由||x﹣1|+2|<5,得﹣5<|x﹣1|+2<5
∴﹣7<|x﹣1|<3,
得不等式的解为﹣2<x<4…
(2)因为任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x)} {y|y=g(x)},
又f(x)=|2x﹣a|+|2x+3|≥|(2x﹣a)﹣(2x+3)|=|a+3|,
g(x)=|x﹣1|+2≥2,所以|a+3|≥2,解得a≥﹣1或a≤﹣5,
所以实数a的取值范围为a≥﹣1或a≤﹣5.…
2017年2月18日
同课章节目录
