宁夏六盘山高级中学2016-2017学年高二下学期开学测试数学理试题 Word版含答案
文档属性
| 名称 | 宁夏六盘山高级中学2016-2017学年高二下学期开学测试数学理试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 203.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-19 21:09:01 | ||
图片预览


文档简介
宁夏六盘山高级中学2016-2017学年第二学期
高二数学理 开学测试卷
学科:理科数学
测试时间:120分钟
满分:150分
一、选择题(本大题共12小题,每小题5分,四个选项中,只有一项是符合题目要求的.)
1.下列命题正确的有(
)
(1)很小的实数可以构成集合;(2)集合与集合是同一个集合;
(3)这些数组成的集合有个元素;(4)集合是指第二和第四象限内的点集
A.个
B.个
C.个
D.个
2.复数等于(
)
A.
B.
C.
D.
3.已知
,
则
(A)
(B)
(C)
(D)
4.在△ABC中,a=1,b=,B=120°,则A等于(
)
A.30°
B.45°
C.60°
D.120°
5.“a
=
1”是“复数(,i为虚数单位)是纯虚数”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.双曲线的渐近线方程为(
)
A.
B.
C.
D.
7.如下图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1那么这个几何体的体积为( )
A.1
B.
C.
D.
8.等比数列{an}的各项均为正数,且a5a6+a2a9=18,则log3a1+log3a2+…+log3a10的值为( )
A.12
B.10
C.8
D.2+log35
9.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1
B.2
C.
D.3
10.将函数y=cos2x的图象上的所有点向左平移个单位长度,再把所得图象向上平移1个单位长度,所得图象的函数解析式是( )
A.y=cos+1
B.y=cos+1
C.y=cos+1
D.y=cos+1
11.椭圆两焦点为
,
,P在椭圆上,若
△的面积的最大值为12,则椭圆方程为(
)
A.
B
.
C
.
D
.
12.
如右图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则下列命题中,错误的是( )
A.点H是△A1BD的垂心
B.AH垂直于平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
二、填空题(本大题共4小题,每小题5分.)
13.若一个正方体的顶点都在同一球面上,则球与该正方体的体积之比为________.
14.随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率为
.
15.已知=(1,1),=(4,1),=(4,5),则与夹角的余弦值为
16.如果关于x的不等式2kx2+kx-<0对一切实数x都成立,那么k的取值范围是____.
三、解答题(解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
在△ABC中,a,b是方程x2-2x+2=0的两根,且2cos(A+B)=1.
(1)求角C的度数;(2)求c;(3)求△ABC的面积.
18.
(本小题满分12分)
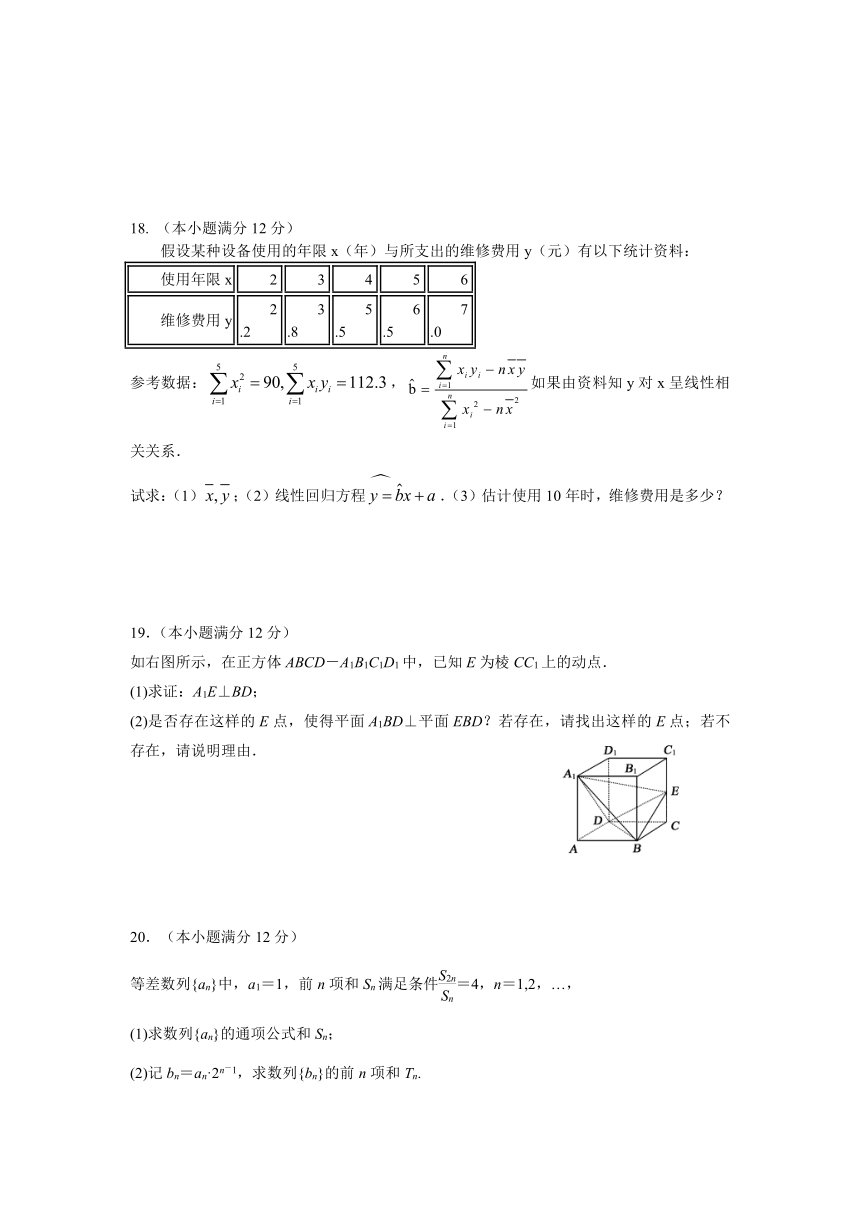
假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
参考数据:,如果由资料知y对x呈线性相关关系.
试求:(1);(2)线性回归方程.(3)估计使用10年时,维修费用是多少?
19.(本小题满分12分)
如右图所示,在正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
(1)求证:A1E⊥BD;
(2)是否存在这样的E点,使得平面A1BD⊥平面EBD?若存在,请找出这样的E点;若不存在,请说明理由.
20.(本小题满分12分)
等差数列{an}中,a1=1,前n项和Sn满足条件=4,n=1,2,…,
(1)求数列{an}的通项公式和Sn;
(2)记bn=an·2n-1,求数列{bn}的前n项和Tn.
21.
(本小题满分12分)
如图,点A,B分别是椭圆的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:且.
(1)求直线AP的方程;
(2)设点M是椭圆长轴AB上一点,点M到直线AP的距离等于,求椭圆上的点到点M的距离d的最小值.
22.
(本小题满分12分)
如右图所示,已知直二面角α-AB-β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4.PC⊥AB,C为垂足,QD
⊥AB,D为垂足.求:
(1)直线PQ与CD所成角的大小;
(2)四面体PCDQ的体积.
参考答案
1.
A
2.B
3.C
4.A
5.A
6.A
7.D
8.B
9.C
10.
C
11.
B
12.
D
13.
π∶2
14.
15.
16.
-317.解:(1)∵2cos(A+B)=1,∴cosC=-.∴角C的度数为120°.
(2)∵a,b是方程x2-2x+2=0的两根,∴a+b=2,ab=2.
由余弦定理,得c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)=12-2=10,∴c=.
(3)S=absinC=.
18.
解:(1)由表中数据可得=(2+3+4+5+6)÷5=4,=(2.2+3.8+5.5+6.5+7.0)÷5=5
(2)由已知可得:=.于是 .
所求线性回归方程为:.
(3)由(2)可得,当x=10时,(万元).
即估计使用10年时,维修费用是12.38万元.
19.
解:连接AC,设AC∩DB=O,连接A1O,OE.
(1)∵A1A⊥底面ABCD,∴A1A⊥BD,又BD⊥AC,
∴BD⊥平面ACEA1,∵A1E 平面ACEA1,∴A1E⊥BD.
(2)当E是CC1的中点时,平面A1BD⊥平面EBD.证明如下:
∵A1B=A1D,EB=ED,O为BD中点,∴A1O⊥BD,EO⊥BD,
∴∠A1OE为二面角A1-BD-E的平面角.
在正方体ABCD-A1B1C1D1中,设棱长为2a,
∵E为棱CC1的中点,由平面几何知识,EO=a,A1O=a,A1E=3a,
∴A1E2=A1O2+EO2,即∠A1OE=90°.∴平面A1BD⊥平面EBD.
20.
解:(1)设等差数列{an}的公差为d,由=4,得=4,所以a2=3a1=3,
且d=a2-a1=2.所以an=a1+(n-1)d=1+2(n-1)=2n-1,
Sn==n2.
(2)由bn=an·2n-1,得bn=(2n-1)·2n-1.
所以Tn=1+3·21+5·22+…+(2n-1)·2n-1,①
2Tn=2+3·22+5·23+…+(2n-3)·2n-1+(2n-1)·2n,②
①-②得
-Tn=1+2·2+2·22+…+2·2n-1-(2n-1)·2n
=2(1+2+22+…+2n-1)-(2n-1)·2n-1
=-(2n-1)·2n-1.
所以Tn=(2n-1)·2n+1-(2n+1-2)
=(n-1)·2n+1-2n+3.
21.
解:
⑴由题意知,,从而
,由题意得,,从而,,因此,直线AP的方程为:,
即.
⑵设,则点M到直线AP的距离为,
而,依题意得解得或(舍去),故.
设椭圆上一点,则,即
,,
所以当时,,即.
22.
解:(1)如下图,在平面β内,作CE
綊DQ,连接PE,QE,则四边形CDQE为平行四边行,所以EQ綊CD,即∠PQE为直线PQ与CD所成的角(或其补角).
∵α⊥β,α∩β=AB,PC⊥AB于C.∴PC⊥β.同理QD⊥α,
又PQ与平面α,β所成的角都为30°,∴∠PQC=30°,∠QPD=30°,
∴CQ=PQ·cos
30°=4×=2,DQ=PQ·sin
30°=4×=2.
在Rt△CDQ中,CD===2,从而EQ=2.
∵QD⊥AB,且CDQE为平行四边形,∴QE⊥CE.又PC⊥β,EQ β,∴EQ⊥PC.
故EQ⊥平面PCE,从而EQ⊥PE.
在Rt△PEQ中,cos∠PQE===.∴∠PQE=45°,
即直线PQ与CD所成角的大小为45°.
(2)在Rt△PCQ中,PQ=4,∠PQC=30°,∴PC=2.而S△CDQ=CD·DQ=×2×2=2,故四面体PCDQ的体积为V=S△CDQ·PC=×2×2=.
高二数学理 开学测试卷
学科:理科数学
测试时间:120分钟
满分:150分
一、选择题(本大题共12小题,每小题5分,四个选项中,只有一项是符合题目要求的.)
1.下列命题正确的有(
)
(1)很小的实数可以构成集合;(2)集合与集合是同一个集合;
(3)这些数组成的集合有个元素;(4)集合是指第二和第四象限内的点集
A.个
B.个
C.个
D.个
2.复数等于(
)
A.
B.
C.
D.
3.已知
,
则
(A)
(B)
(C)
(D)
4.在△ABC中,a=1,b=,B=120°,则A等于(
)
A.30°
B.45°
C.60°
D.120°
5.“a
=
1”是“复数(,i为虚数单位)是纯虚数”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.双曲线的渐近线方程为(
)
A.
B.
C.
D.
7.如下图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1那么这个几何体的体积为( )
A.1
B.
C.
D.
8.等比数列{an}的各项均为正数,且a5a6+a2a9=18,则log3a1+log3a2+…+log3a10的值为( )
A.12
B.10
C.8
D.2+log35
9.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1
B.2
C.
D.3
10.将函数y=cos2x的图象上的所有点向左平移个单位长度,再把所得图象向上平移1个单位长度,所得图象的函数解析式是( )
A.y=cos+1
B.y=cos+1
C.y=cos+1
D.y=cos+1
11.椭圆两焦点为
,
,P在椭圆上,若
△的面积的最大值为12,则椭圆方程为(
)
A.
B
.
C
.
D
.
12.
如右图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则下列命题中,错误的是( )
A.点H是△A1BD的垂心
B.AH垂直于平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
二、填空题(本大题共4小题,每小题5分.)
13.若一个正方体的顶点都在同一球面上,则球与该正方体的体积之比为________.
14.随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率为
.
15.已知=(1,1),=(4,1),=(4,5),则与夹角的余弦值为
16.如果关于x的不等式2kx2+kx-<0对一切实数x都成立,那么k的取值范围是____.
三、解答题(解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
在△ABC中,a,b是方程x2-2x+2=0的两根,且2cos(A+B)=1.
(1)求角C的度数;(2)求c;(3)求△ABC的面积.
18.
(本小题满分12分)
假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x
2
3
4
5
6
维修费用y
2.2
3.8
5.5
6.5
7.0
参考数据:,如果由资料知y对x呈线性相关关系.
试求:(1);(2)线性回归方程.(3)估计使用10年时,维修费用是多少?
19.(本小题满分12分)
如右图所示,在正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
(1)求证:A1E⊥BD;
(2)是否存在这样的E点,使得平面A1BD⊥平面EBD?若存在,请找出这样的E点;若不存在,请说明理由.
20.(本小题满分12分)
等差数列{an}中,a1=1,前n项和Sn满足条件=4,n=1,2,…,
(1)求数列{an}的通项公式和Sn;
(2)记bn=an·2n-1,求数列{bn}的前n项和Tn.
21.
(本小题满分12分)
如图,点A,B分别是椭圆的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:且.
(1)求直线AP的方程;
(2)设点M是椭圆长轴AB上一点,点M到直线AP的距离等于,求椭圆上的点到点M的距离d的最小值.
22.
(本小题满分12分)
如右图所示,已知直二面角α-AB-β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4.PC⊥AB,C为垂足,QD
⊥AB,D为垂足.求:
(1)直线PQ与CD所成角的大小;
(2)四面体PCDQ的体积.
参考答案
1.
A
2.B
3.C
4.A
5.A
6.A
7.D
8.B
9.C
10.
C
11.
B
12.
D
13.
π∶2
14.
15.
16.
-3
(2)∵a,b是方程x2-2x+2=0的两根,∴a+b=2,ab=2.
由余弦定理,得c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)=12-2=10,∴c=.
(3)S=absinC=.
18.
解:(1)由表中数据可得=(2+3+4+5+6)÷5=4,=(2.2+3.8+5.5+6.5+7.0)÷5=5
(2)由已知可得:=.于是 .
所求线性回归方程为:.
(3)由(2)可得,当x=10时,(万元).
即估计使用10年时,维修费用是12.38万元.
19.
解:连接AC,设AC∩DB=O,连接A1O,OE.
(1)∵A1A⊥底面ABCD,∴A1A⊥BD,又BD⊥AC,
∴BD⊥平面ACEA1,∵A1E 平面ACEA1,∴A1E⊥BD.
(2)当E是CC1的中点时,平面A1BD⊥平面EBD.证明如下:
∵A1B=A1D,EB=ED,O为BD中点,∴A1O⊥BD,EO⊥BD,
∴∠A1OE为二面角A1-BD-E的平面角.
在正方体ABCD-A1B1C1D1中,设棱长为2a,
∵E为棱CC1的中点,由平面几何知识,EO=a,A1O=a,A1E=3a,
∴A1E2=A1O2+EO2,即∠A1OE=90°.∴平面A1BD⊥平面EBD.
20.
解:(1)设等差数列{an}的公差为d,由=4,得=4,所以a2=3a1=3,
且d=a2-a1=2.所以an=a1+(n-1)d=1+2(n-1)=2n-1,
Sn==n2.
(2)由bn=an·2n-1,得bn=(2n-1)·2n-1.
所以Tn=1+3·21+5·22+…+(2n-1)·2n-1,①
2Tn=2+3·22+5·23+…+(2n-3)·2n-1+(2n-1)·2n,②
①-②得
-Tn=1+2·2+2·22+…+2·2n-1-(2n-1)·2n
=2(1+2+22+…+2n-1)-(2n-1)·2n-1
=-(2n-1)·2n-1.
所以Tn=(2n-1)·2n+1-(2n+1-2)
=(n-1)·2n+1-2n+3.
21.
解:
⑴由题意知,,从而
,由题意得,,从而,,因此,直线AP的方程为:,
即.
⑵设,则点M到直线AP的距离为,
而,依题意得解得或(舍去),故.
设椭圆上一点,则,即
,,
所以当时,,即.
22.
解:(1)如下图,在平面β内,作CE
綊DQ,连接PE,QE,则四边形CDQE为平行四边行,所以EQ綊CD,即∠PQE为直线PQ与CD所成的角(或其补角).
∵α⊥β,α∩β=AB,PC⊥AB于C.∴PC⊥β.同理QD⊥α,
又PQ与平面α,β所成的角都为30°,∴∠PQC=30°,∠QPD=30°,
∴CQ=PQ·cos
30°=4×=2,DQ=PQ·sin
30°=4×=2.
在Rt△CDQ中,CD===2,从而EQ=2.
∵QD⊥AB,且CDQE为平行四边形,∴QE⊥CE.又PC⊥β,EQ β,∴EQ⊥PC.
故EQ⊥平面PCE,从而EQ⊥PE.
在Rt△PEQ中,cos∠PQE===.∴∠PQE=45°,
即直线PQ与CD所成角的大小为45°.
(2)在Rt△PCQ中,PQ=4,∠PQC=30°,∴PC=2.而S△CDQ=CD·DQ=×2×2=2,故四面体PCDQ的体积为V=S△CDQ·PC=×2×2=.
同课章节目录
