6.2平行四边形的判定 课时1同步练习
文档属性
| 名称 | 6.2平行四边形的判定 课时1同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 422.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-22 10:20:11 | ||
图片预览


文档简介
第二节 平行四边形的判定
第1课时 用边的关系判定平行四边形
基础检测
知识点1由两组对边关系判定平行四边形
1.要判定四边形是平行四边形,若从边的位置关系的角度去判定,需两组对边分别________.若从边的数量关系的角度去判定,需两组对边分别________.?
2.在四边形ABCD中,AD∥BC,当满足条件( )时,四边形ABCD是平行四边形.
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
3.A,B,C是平面内不在同一条直线上的三点,D是平面内任意一点,若A,B,C,D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个 B.2个 C.3个 D.4个
4.下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形 B.两个直角三角形
C.两个锐角三角形 D.两个全等三角形
5.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=________.?
6.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图,在四边形ABCD中,BC=AD,
AB=________.?
求证:四边形ABCD是________四边形.?
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明.
(3)用文字叙述所证命题的逆命题为?
.?
知识点2由一组对边关系判定平行四边形
7.一组对边________且________的四边形是平行四边形. ?
8.在四边形ABCD中,AD=BC,若四边形ABCD是平行四边形,则还应满足( )
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
9.不能判定四边形ABCD为平行四边形的条件是( )
A.AB=CD,AD=BC
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC
D.AD=BC,AD∥BC
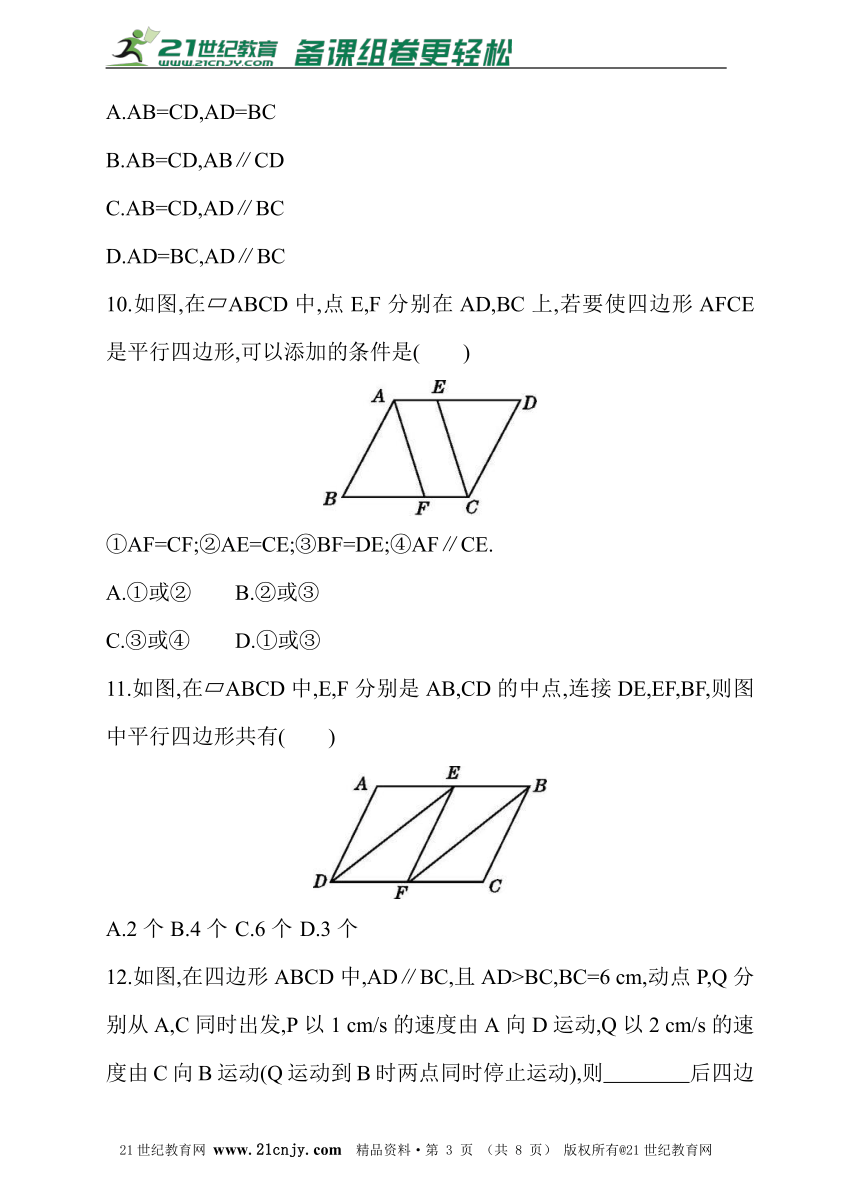
10.如图,在?ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或② B.②或③
C.③或④ D.①或③
11.如图,在?ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则图中平行四边形共有( )
A.2个 B.4个 C.6个 D.3个
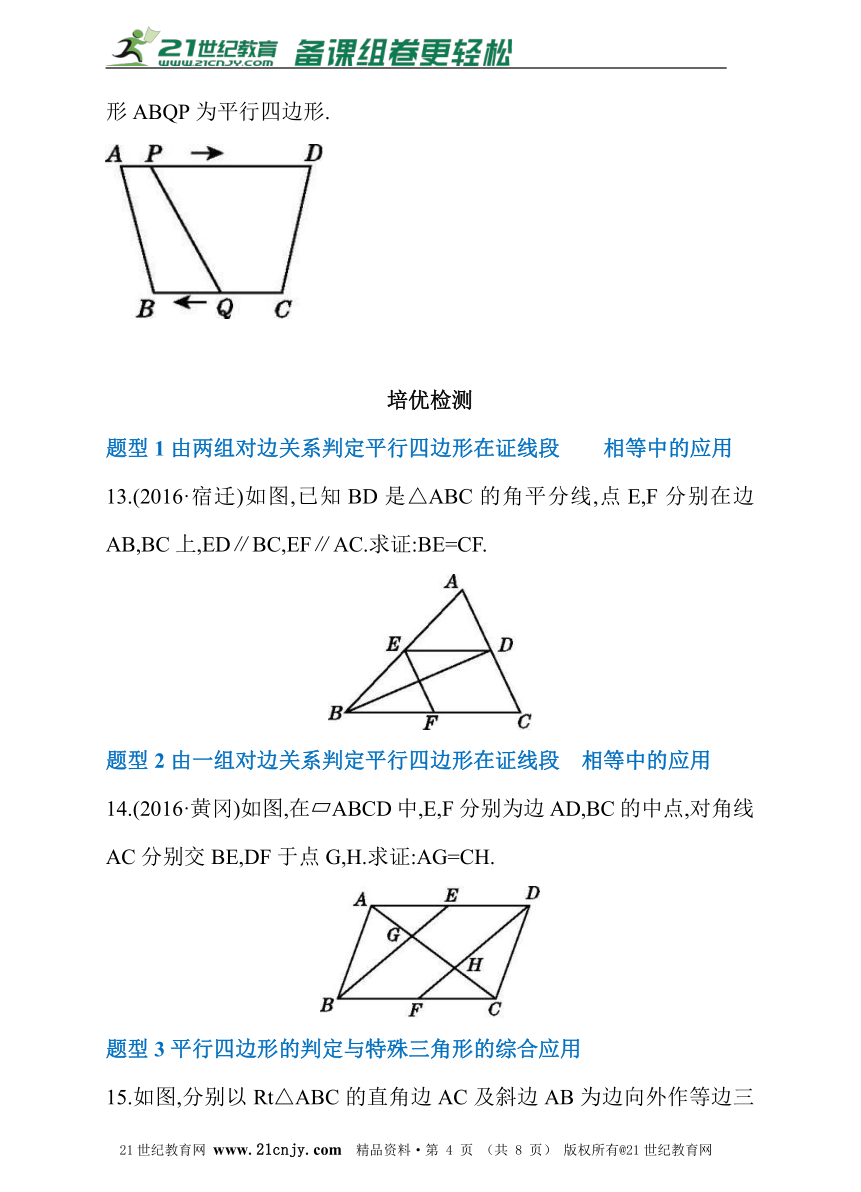
12.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2 cm/s的速度由C向B运动(Q运动到B时两点同时停止运动),则 后四边形ABQP为平行四边形.?
培优检测
题型1由两组对边关系判定平行四边形在证线段 相等中的应用
13.(2016·宿迁)如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED∥BC,EF∥AC.求证:BE=CF.
题型2由一组对边关系判定平行四边形在证线段 相等中的应用
14.(2016·黄冈)如图,在?ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH.
题型3平行四边形的判定与特殊三角形的综合应用
15.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD及等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
16.如图,在梯形ABCD中,AD∥BC,AD=24 cm,BC=30 cm,点P自点A向D以1 cm/s的速度运动,到D点即停止.点Q自点C向B以2 cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.P,Q同时出发,几秒后其中一个四边形为平行四边形?
参考答案
1.【答案】平行;相等
2.【答案】D 3.【答案】C 4.【答案】D
5.【答案】4或-2
6.(1)解:CD;平行
(2)证明:如图,连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形.
(3)平行四边形的两组对边分别相等
7.【答案】平行;相等
8.【答案】C 9.【答案】C
10.【答案】C 11.【答案】B
12.【答案】2 s
13.证明:∵ED∥BC,EF∥AC,
∴四边形EFCD是平行四边形.
∴DE=CF.
∵BD平分∠ABC,
∴∠EBD=∠DBC.
∵DE∥BC,∴∠EDB=∠DBC.
∴∠EBD=∠EDB.
∴BE=ED.
∴BE=CF.
14.证明:∵E,F分别是AD,BC的中点,
∴AE=DE=AD,CF=BF=BC.
又∵AD∥BC,且AD=BC.
∴DE∥BF,DE=BF,AE=CF.
∴四边形BEDF是平行四边形.
∴∠BED=∠DFB.
∴∠AEG=∠CFH.
又∵AD∥BC,∴∠EAG=∠FCH.
在△AGE和△CHF中,
∴△AGE≌△CHF.
∴AG=CH.
15.证明:(1)∵在Rt△ABC中,∠BAC=30°,
∴BC=AB.
∵△ABE是等边三角形,EF⊥AB,
∴AB=EB,BF=AB.
∴BC=BF.
在Rt△ACB和Rt△EFB中,
∴Rt△ACB≌Rt△EFB(HL).∴AC=EF.
(2)∵△ADC是等边三角形,∴∠DAC=60°,AC=AD.
∴AD=EF.∵∠BAC=30°,
∴∠DAF=∠DAC+∠BAC=90°.
∴∠DAF=∠AFE.∴AD∥EF.
∴四边形ADFE是平行四边形.
16.解:设P,Q同时出发,t s后四边形PDCQ或四边形APQB是平行四边形.
根据已知得到AP=t cm,PD=(24-t)cm,CQ=2t cm,BQ=(30-2t)cm.
①若四边形PDCQ是平行四边形,则PD=CQ,
∴24-t=2t,∴t=8,
∴8 s后四边形PDCQ是平行四边形;
②若四边形APQB是平行四边形,则AP=BQ,
∴t=30-2t,∴t=10,
∴10 s后四边形APQB是平行四边形.
∴出发8 s或10 s后其中一个四边形是平行四边形.
第1课时 用边的关系判定平行四边形
基础检测
知识点1由两组对边关系判定平行四边形
1.要判定四边形是平行四边形,若从边的位置关系的角度去判定,需两组对边分别________.若从边的数量关系的角度去判定,需两组对边分别________.?
2.在四边形ABCD中,AD∥BC,当满足条件( )时,四边形ABCD是平行四边形.
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
3.A,B,C是平面内不在同一条直线上的三点,D是平面内任意一点,若A,B,C,D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个 B.2个 C.3个 D.4个
4.下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形 B.两个直角三角形
C.两个锐角三角形 D.两个全等三角形
5.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=________.?
6.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图,在四边形ABCD中,BC=AD,
AB=________.?
求证:四边形ABCD是________四边形.?
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明.
(3)用文字叙述所证命题的逆命题为?
.?
知识点2由一组对边关系判定平行四边形
7.一组对边________且________的四边形是平行四边形. ?
8.在四边形ABCD中,AD=BC,若四边形ABCD是平行四边形,则还应满足( )
A.∠A+∠C=180° B.∠B+∠D=180°
C.∠A+∠B=180° D.∠A+∠D=180°
9.不能判定四边形ABCD为平行四边形的条件是( )
A.AB=CD,AD=BC
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC
D.AD=BC,AD∥BC
10.如图,在?ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或② B.②或③
C.③或④ D.①或③
11.如图,在?ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则图中平行四边形共有( )
A.2个 B.4个 C.6个 D.3个
12.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2 cm/s的速度由C向B运动(Q运动到B时两点同时停止运动),则 后四边形ABQP为平行四边形.?
培优检测
题型1由两组对边关系判定平行四边形在证线段 相等中的应用
13.(2016·宿迁)如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED∥BC,EF∥AC.求证:BE=CF.
题型2由一组对边关系判定平行四边形在证线段 相等中的应用
14.(2016·黄冈)如图,在?ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH.
题型3平行四边形的判定与特殊三角形的综合应用
15.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD及等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
16.如图,在梯形ABCD中,AD∥BC,AD=24 cm,BC=30 cm,点P自点A向D以1 cm/s的速度运动,到D点即停止.点Q自点C向B以2 cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.P,Q同时出发,几秒后其中一个四边形为平行四边形?
参考答案
1.【答案】平行;相等
2.【答案】D 3.【答案】C 4.【答案】D
5.【答案】4或-2
6.(1)解:CD;平行
(2)证明:如图,连接BD.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形.
(3)平行四边形的两组对边分别相等
7.【答案】平行;相等
8.【答案】C 9.【答案】C
10.【答案】C 11.【答案】B
12.【答案】2 s
13.证明:∵ED∥BC,EF∥AC,
∴四边形EFCD是平行四边形.
∴DE=CF.
∵BD平分∠ABC,
∴∠EBD=∠DBC.
∵DE∥BC,∴∠EDB=∠DBC.
∴∠EBD=∠EDB.
∴BE=ED.
∴BE=CF.
14.证明:∵E,F分别是AD,BC的中点,
∴AE=DE=AD,CF=BF=BC.
又∵AD∥BC,且AD=BC.
∴DE∥BF,DE=BF,AE=CF.
∴四边形BEDF是平行四边形.
∴∠BED=∠DFB.
∴∠AEG=∠CFH.
又∵AD∥BC,∴∠EAG=∠FCH.
在△AGE和△CHF中,
∴△AGE≌△CHF.
∴AG=CH.
15.证明:(1)∵在Rt△ABC中,∠BAC=30°,
∴BC=AB.
∵△ABE是等边三角形,EF⊥AB,
∴AB=EB,BF=AB.
∴BC=BF.
在Rt△ACB和Rt△EFB中,
∴Rt△ACB≌Rt△EFB(HL).∴AC=EF.
(2)∵△ADC是等边三角形,∴∠DAC=60°,AC=AD.
∴AD=EF.∵∠BAC=30°,
∴∠DAF=∠DAC+∠BAC=90°.
∴∠DAF=∠AFE.∴AD∥EF.
∴四边形ADFE是平行四边形.
16.解:设P,Q同时出发,t s后四边形PDCQ或四边形APQB是平行四边形.
根据已知得到AP=t cm,PD=(24-t)cm,CQ=2t cm,BQ=(30-2t)cm.
①若四边形PDCQ是平行四边形,则PD=CQ,
∴24-t=2t,∴t=8,
∴8 s后四边形PDCQ是平行四边形;
②若四边形APQB是平行四边形,则AP=BQ,
∴t=30-2t,∴t=10,
∴10 s后四边形APQB是平行四边形.
∴出发8 s或10 s后其中一个四边形是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
