6.3三角形的中位线同步练习

第三节 三角形的中位线
基础检测
知识点1三角形中位线的性质
1.连接三角形两边中点的线段叫做三角形的_________.三角形的中位线_________第三边,且等于第三边的_________.?
2.如图,在△ABC中,AB=8,点D,E分别是BC,CA的中点,连接DE,则DE=_________.?
3.如图,已知四边形ABCD是平行四边形,对角线AC,BD交于点O,E是BC的中点,以下说法错误的是(　　)
A.OE=DC B.OA=OC
C.∠BOE=∠OBA D.∠OBE=∠OCE
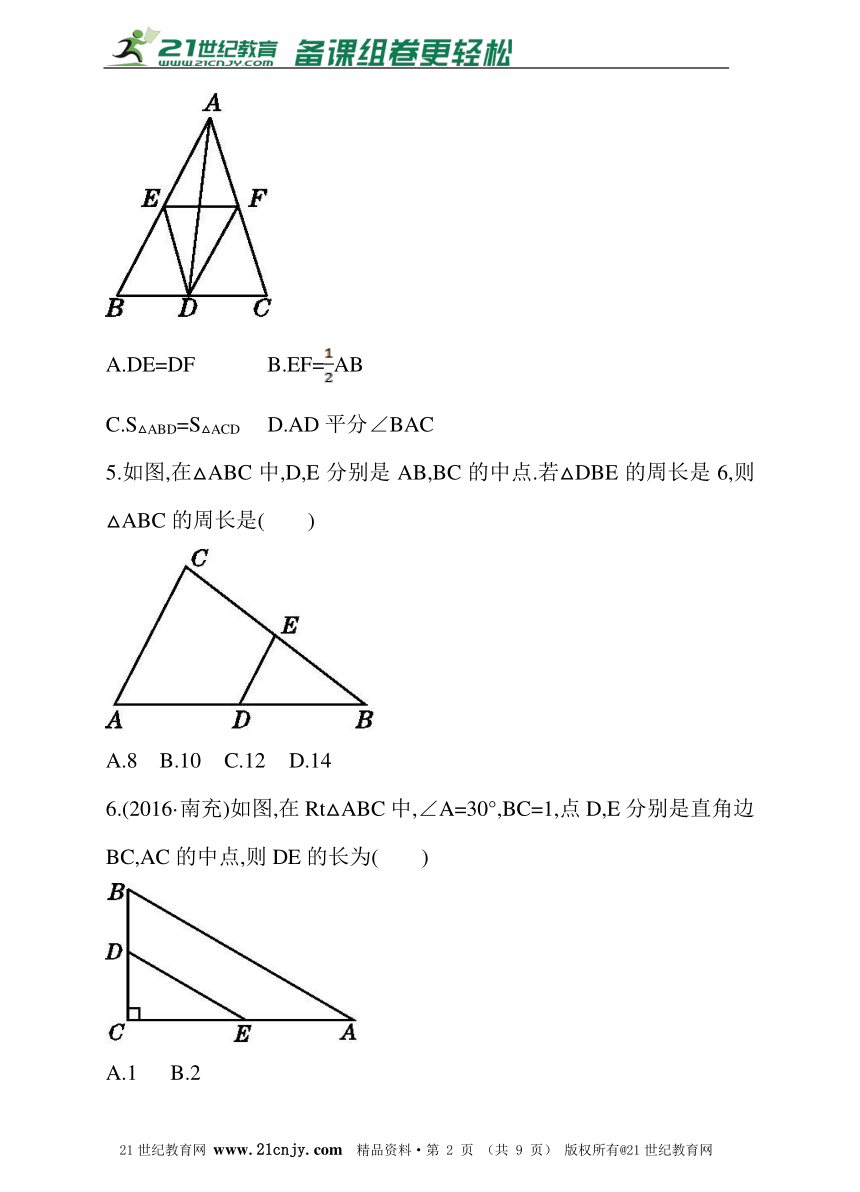
4.如图,点D,E,F分别为△ABC各边的中点,下列说法正确的是(　　)
A.DE=DF B.EF=AB
C.S△ABD=S△ACD D.AD平分∠BAC
5.如图,在△ABC中,D,E分别是AB,BC的中点.若△DBE的周长是6,则△ABC的周长是(　　)
A.8 B.10 C.12 D.14
6.(2016·南充)如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为(　　)
A.1 B.2
C. D.1+
7.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,以下结论成立的是(　　)
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不变
D.线段EF的长与点P的位置有关
知识点2三角形中位线在四边形中的应用
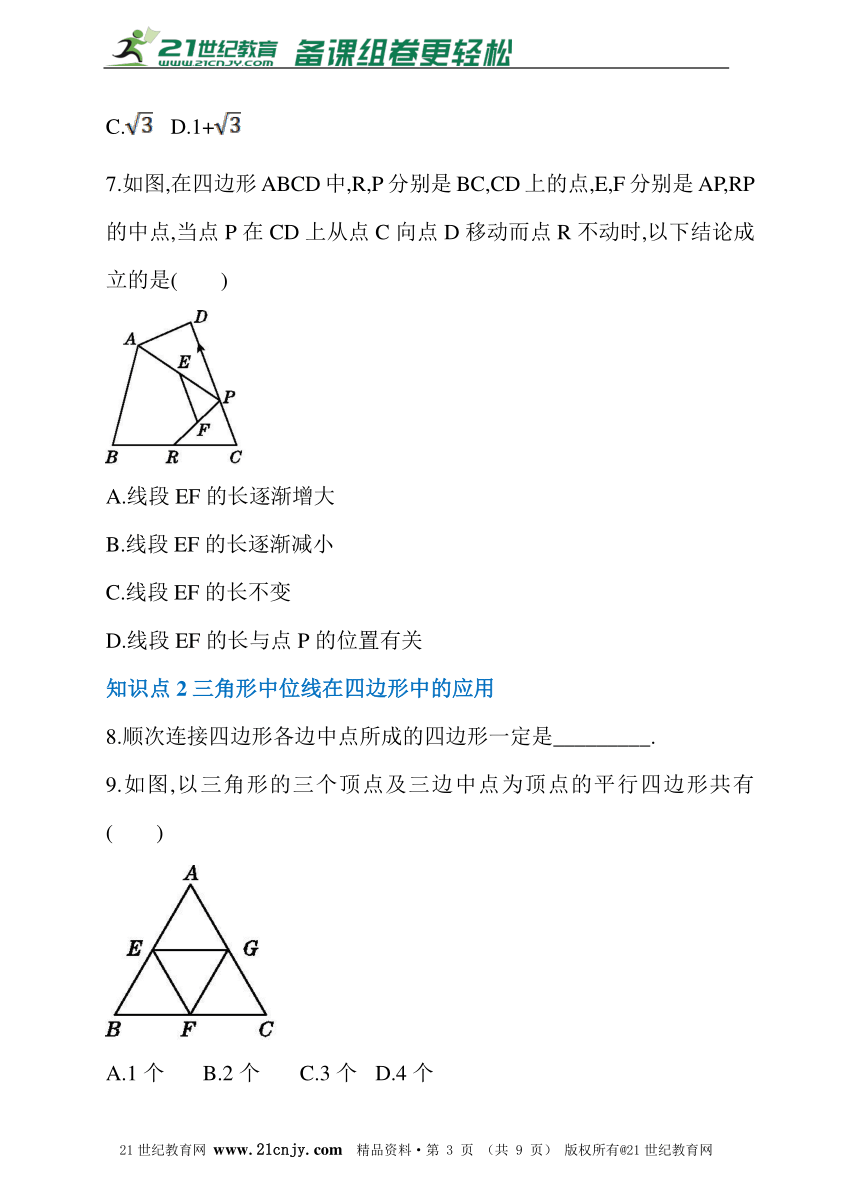
8.顺次连接四边形各边中点所成的四边形一定是_________.?
9.如图,以三角形的三个顶点及三边中点为顶点的平行四边形共有(　　)
A.1个 B.2个 C.3个 D.4个
10.如图,已知E,F,G,H分别为四边形ABCD各边的中点,若AC=10 cm,BD=12 cm,则四边形EFGH的周长为(　　)
A.10 cm B.11 cm C.12 cm D.22 cm
11.如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是(　　)
A.15° B.20° C.25° D.30°
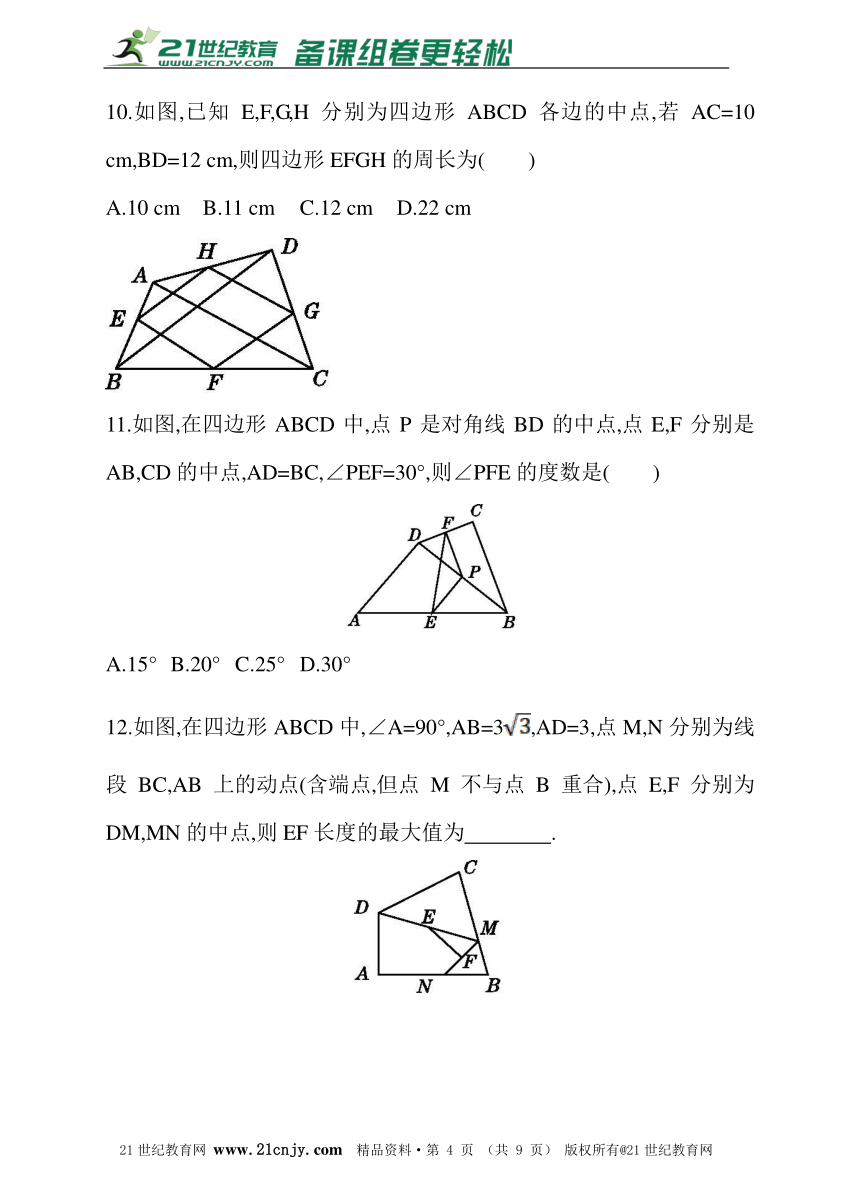
12.如图,在四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为　　　　.
培优检测
题型1三角形中位线在求线段长中的应用
13.如图,等边三角形ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接DE,CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
题型2三角形中位线在证线段倍分关系中的应用
14.如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.求证:
(1)AE=AF;
(2)BE=(AB+AC).
题型3构造中位线法在证线段相等中的应用
15.如图,在四边形ABCD中,AC=BD,M,N分别是AB,CD的中点,MN分别交BD和AC于点E,F,对角线AC和BD相交于点G,则GE和GF相等吗?为什么?
16.如图,在?ABCD中,E是DC的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
参考答案
1.【答案】中位线;平行于;一半
2.【答案】4 3.【答案】D
4.【答案】C 5.【答案】C
6.【答案】A 7.【答案】C
8.【答案】平行四边形
9.【答案】C 10.【答案】D 11.【答案】D
12.【答案】3
13.(1)证明:∵D,E分别为AB,AC的中点,
∴DE是△ABC的中位线.
∴DE=BC=1.
∵CF=BC=1,
∴DE=CF.
(2)解:由(1)知DE是△ABC的中位线,
∴DE∥CF.
又∵DE=CF,
∴四边形CDEF是平行四边形.
∴CD=EF.
在等边三角形ABC中,D是AB的中点,
∴CD⊥AB,BD=AB=1.
∴CD==.
∴EF=.
14.证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE.
∴∠AEF=∠AFE.
∴AE=AF.
(2)如图,在BE的延长线上截取EG=BE,并连接CG.
∵BM=CM,∴EM为△BCG的中位线.
∴EM∥CG.∴∠AGC=∠AEF,∠ACG=∠AFE.
∵∠AEF=∠AFE,
∴∠AGC=∠ACG.
∴AG=AC.
∴BE=BG=(AB+AG)=(AB+AC).
15.解:GE=GF.理由如下:
取BC的中点P,连接MP,NP.
∵AM=BM,BP=CP,
∴MP∥AC,MP=AC.
同理NP∥BD,NP=BD.
∵AC=BD,∴MP=NP.
∴∠PMN=∠PNM.
∵MP∥AC,NP∥BD,
∴∠GFE=∠PMN,∠GEF=∠PNM.
∴∠GFE=∠GEF.
∴GE=GF.
16.证明:如图,取BE的中点H,连接FH,CH.
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线.
∴FH∥AB且FH=AB.
在?ABCD中,AB∥DC,AB=DC.
又∵点E是DC的中点,
∴EC=DC=AB.
∴FH=EC.
又∵AB∥DC,∴FH∥EC.
∴四边形EFHC是平行四边形.
∴GF=GC.